4.5: Незворотні процеси

Template:DeVoeMathJax

Ми знаємо, що під час оборотного процесу замкнутої системи кожна нескінченно мала зміна ентропії\(\dif S\) дорівнює,\(\dq/T\bd\) а\(\Del S\) кінцева зміна дорівнює інтегралу\(\int(\dq/T\bd)\) —але що ми можемо сказати про\(\dif S\) незворотний процес?\(\Del S\)

Виведення цього розділу покаже, що для нескінченно малої незворотної зміни замкнутої системи,\(\dif S\) більше\(\dq/T\bd\), ніж, а для\(\Del S\) всього процесу більше\(\int(\dq/T\bd)\). Тобто рівності, які застосовуються до оборотного процесу, замінюються, для незворотного процесу, нерівностями.

Виведення починається з незворотних процесів, які є адіабатичними, а потім поширюється на незворотні процеси в цілому.

4.5.1 Незворотні адіабатичні процеси

Розглянемо довільний незворотний адіабатичний процес замкнутої системи, що починається з певного початкового стану А. Кінцевий стан B залежить від шляху цього процесу. Бажаємо дослідити ознаку зміни ентропії\(\Del S\subs{A\(\ra\) B}\). Наші міркування залежатимуть від того, чи є робота під час процесу.

Якщо є робота по будь-якому нескінченно малому елементу шляху незворотного адіабатичного процесу (\(\dw \ne 0\)), ми знаємо з досвіду, що ця робота була б іншою, якби координати роботи або координати змінювалися з іншою швидкістю, тому що розсіювання енергії від внутрішнього тертя тоді було б іншим. У межі нескінченної повільності адіабатичний процес з початковим станом А і однаковою зміною робочих координат став би оборотним, а чиста робота і кінцева внутрішня енергія відрізнялися б від незворотного процесу. Оскільки кінцевий стан оборотного адіабатичного процесу відрізняється від В, немає оборотного адіабатичного шляху з роботою між станами А і В.

Всі стани оборотного процесу, включаючи початковий і кінцевий стани, повинні бути рівноважними. Тому існує концептуальна складність розгляду оборотних шляхів між двома станами, якщо будь-який з цих станів є нерівноважними станами. У такому випадку ми будемо вважати, що стан було замінено на стан обмеженої рівноваги тієї ж ентропії, що описано в п. 4.4.3.

Якщо ж, з іншого боку, немає роботи по якомусь нескінченно малому елементу шляху незворотного адіабатичного процесу (\(\dw{=}0\)), то процес відбувається при постійній внутрішній енергії\(U\) в ізольованій системі. Реверсивний межа не може бути досягнутий без тепла або роботи (п. 3.2.1). Таким чином, будь-яка оборотна адіабатична зміна від стану А вимагатиме роботи, спричиняючи зміну\(U\) та запобігаючи досягненню системи стану B будь-яким оборотним адіабатичним шляхом.

Тож незалежно від того, чи передбачає незворотний адіабатичний процес А\(\ra\) В, не існує оборотного адіабатичного шляху між А і Б. Єдиний оборотний шлях між цими станами повинен бути неадіабатичним. Звідси випливає, що зміна ентропії\(\Del S\subs{A\(\ra\) B}\), задана значенням\(\dq/T\bd\) інтегрованого по оборотному шляху від А до Б, не може бути нулем.

Далі ми запитуємо, чи може\(\Del S\subs{A\(\ra\) B}\) бути негативним. У кожному нескінченно малому шляху елемент необоротного адіабатичного процесу A\(\ra\) B,\(\dq\) дорівнює нулю, а інтеграл\(\int_{\tx{A}}^{\tx{B}}(\dq/T\bd)\) по шляху цього процесу дорівнює нулю. Припустимо, система завершує цикл, повертаючись по іншому, оборотному шляху від стану B назад до стану А. Нерівність Клаузіуса (ур. 4.4.3) говорить нам, що в цьому випадку інтеграл\(\int_{\tx{B}}^{\tx{A}}(\dq/T\bd)\) вздовж оборотного шляху не може бути позитивним. Але цей інтеграл для оборотного шляху дорівнює\(-\Del S\subs{A\(\ra\) B}\), тому\(\Del S\subs{A\(\ra\) B}\) не може бути від'ємним.

Зроблено висновок, що оскільки зміна ентропії незворотного адіабатичного процесу A\(\ra\) B не може бути нульовим, і вона не може бути негативною, вона повинна бути позитивною.

При цьому виведенні початковий стан А є довільним, а кінцевий стан В досягається незворотним адіабатичним процесом. Якщо два стани лише нескінченно відрізняються, то зміна нескінченно мала. Таким чином, для нескінченно малих змін, які є незворотними і адіабатичними,\(\dif S\) повинні бути позитивними.

4.5.2 Незворотні процеси в цілому

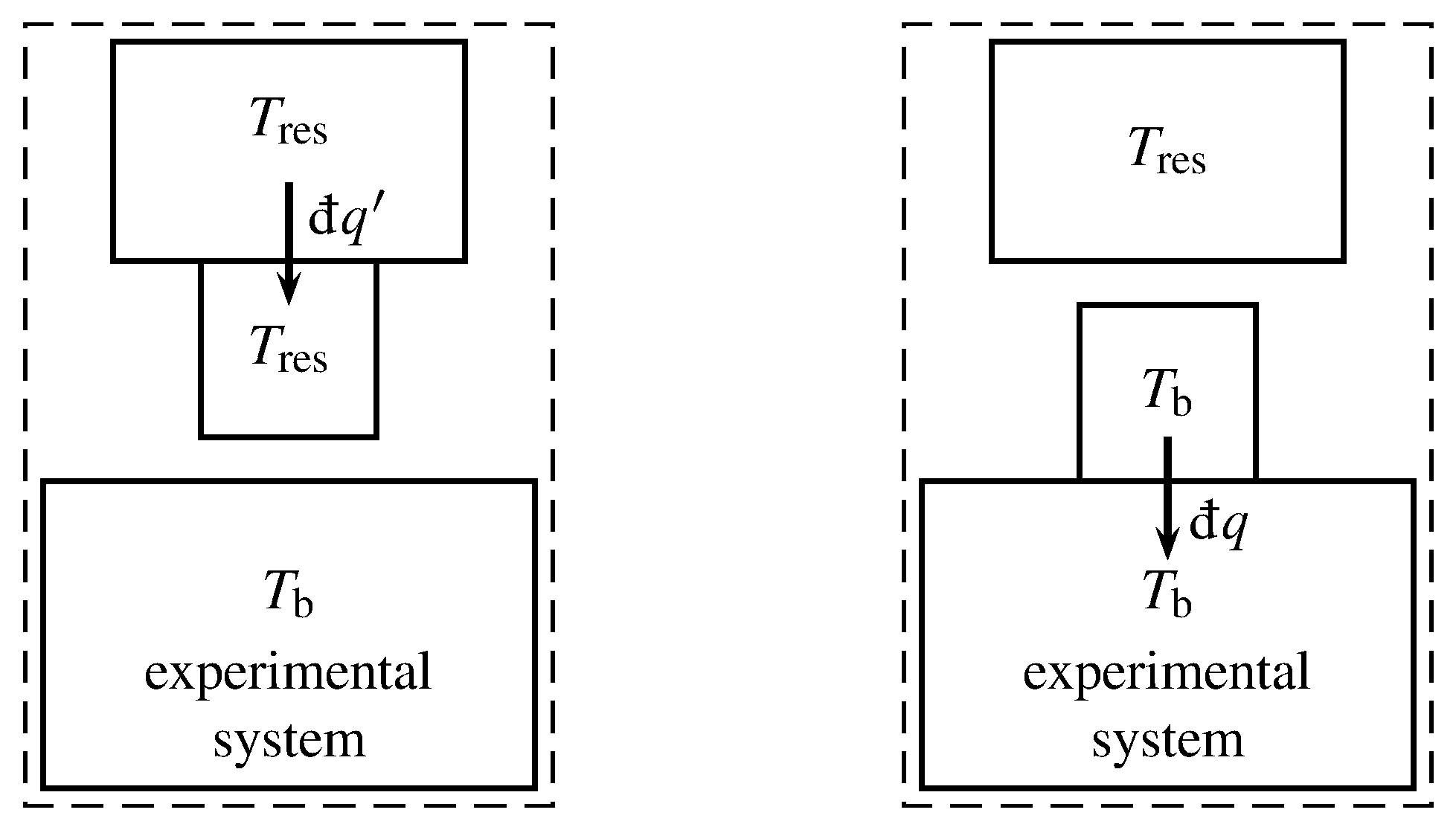
Малюнок 4.11 Надсистема, що включає експериментальну систему, двигун Карно (квадратна коробка) та тепловий резервуар. Пунктирним прямокутником позначається межа надсистеми.

Для лікування незворотного процесу замкнутої системи, яка носить неадіабатичний характер, діємо наступним чином. Як і в п. 4.4.1, ми використовуємо двигун Карно для передачі тепла через межу експериментальної системи. Рухаємо межу надсистеми рис. 4.8 так, щоб надсистема тепер включала в себе експериментальну систему, двигун Карно, і тепловий резервуар постійної температури\(T\subs{res}\), як зображено на рис.4.11. Під час незворотної зміни експериментальної системи двигун Карно зазнає безліч нескінченно малих циклів. Під час кожного циклу двигун Карно обмінюється теплом\(\dq'\) за температурою\(T\subs{res}\) з тепловим резервуаром і тепло\(\dq\) при температурі\(T\bd\) з експериментальною системою, як зазначено на малюнку. Ми використовуємо знак умовності, який\(\dq'\) є позитивним, якщо тепло передається двигуну Карно, і\(\dq\) є позитивним, якщо тепло передається експериментальній системі, в напрямках стрілок на малюнку.

Надсистема обмінюється роботою, але не теплом, зі своїм оточенням. Протягом одного нескінченно малого циклу двигуна Карно зміна чистої ентропії двигуна Карно дорівнює нулю, зміна ентропії експериментальної системи -, тепло\(\dif S\), що передається між двигуном Карно і експериментальною системою, є, і тепло\(\dq\), що передається між тепловим резервуаром і Двигун Карно задається\(\dq'=T\subs{res}\dq/T\bd\) (ур. 4.4.1). Тепловіддача між тепловим резервуаром і двигуном Карно є оборотною, тому зміна ентропії теплового резервуара становить\ begin {рівняння}\ dif S\ subs {res} = -\ frac {\ dq'} {T\ dq'} {T\ bd}\ tag {4.5.1}\ end {рівняння} Зміна ентропії надсистеми є сумою ентропійних змін його частини:\ begin {рівняння}\ dif S\ subs {ss} =\ dif S +\ dif S\ subs {res} =\ dif S -\ frac {\ dq} {T\ bd}\ tag {4.5.2}\ end {рівняння} Процес всередині надсистеми є адіабатичним і включає незворотні зміни в експериментальній системі, тому відповідно до висновків п. 4.5.1,\(\dif S\subs{ss}\) позитивний. Рівняння 4.5.2 потім показує\(\dif S\), що нескінченно мала зміна ентропії під час незворотної зміни експериментальної системи повинна бути більшою за\(\dq/T\bd\):\ begin {gather}\ s {\ dif S >\ frac {\ dq} {T\ bd}}\ tag {4.5.3}\ cond {(незворотна зміна, замкнута система)}\ end {gather} Це співвідношення включає в себе випадок незворотної адіабатичної зміни, оскільки він показує, що якщо\(\dq\) дорівнює нулю,\(\dif S\) більше нуля.

Інтегруючи обидві сторони еквалайзера 4.5.3 між початковим і кінцевим станами незворотного процесу, отримано відношення для зміни скінченної ентропії, що відповідає багатьом нескінченно малим циклам двигуна Карно:\ begin {gather}\ s {\ Del S >\ int\! \ frac {\ dq} {T\ bd}}\ tag {4.5.4}\ cond {(незворотний процес, закрита система)}\ end {зібрати}