12.5: Інший погляд на принцип Ле Шательє

Коли ми застосовуємо принцип Ле Шательє, ми уявляємо собі рівноважну систему, на яку ми накладаємо деякі покрокові зміни. Відразу після накладення цієї зміни ми ізолюємо систему від усіх подальших взаємодій з її оточенням. Ця ізольована система є гіпотетичною конструкцією, яку можна лише наблизити в будь-якому реальному експерименті. Він має своєрідні особливості: Хоча змінена та ізольована система має властивості оригінальної системи, вона також може зазнати подальших змін, які оригінальна система не могла. Гіпотетична ізольована система вже не знаходиться в рівновазі; вона може піддаватися спонтанному процесу подальших змін, поки не досягне нового положення рівноваги. Принцип стверджує, що ця подальша зміна виступає проти нав'язаної зміни.

Принцип за своєю суттю якісний. Це сприяє його корисності в тому, що нам не потрібно мати кількісні дані, щоб використовувати їх. Однак якісне прогнозування менш корисне, ніж кількісне. Давайте спробуємо застосувати наші кількісні моделі, засновані на другому законі, до послідовності змін, передбачених принципом Ле Шательє. Почнемо з повторення принципу більш математичною мовою. Потім ми проілюструємо ці ідеї для конкретного випадку рівноваги пара — рідина з температурою та тиском як незалежними змінними.

Припустимо\(W\), що\(X\),,\(Y\), і\(Z\) є сукупністю термодинамічних змінних, які є адекватними для визначення стану системи. У будь-якому стані рівноваги ентропія системи тоді є функцією цих змінних; ми маємо\(S=S\left(W,X,Y,Z\right)\). Для нинішніх цілей ми припускаємо, що ми знаємо функцію\(S\left(W,X,Y,Z\right)\). Враховуючи невеликі зміни\(dW\),\(dX\),\(dY\),\(dZ\), і, в незалежних змінних, ми можемо знайти зміни\(dS\) для оборотного переходу від\(\left(W,X,Y,Z\right)\) до\(\left(W+dW,X+dX,Y+dY,Z+dZ\right)\):

\[dS={\left(\frac{\partial S}{\partial W}\right)}_{XYZ}dW+{\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX+{\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY+{\left(\frac{\partial S}{\partial Z}\right)}_{WXY}dZ\]

Коли ми нав'язуємо зміни, створюючи гіпотетичну ізольовану систему, ми уявляємо, що якась характеристика системи змінюється миттєво, і що вона робить це, не змінюючи інших властивостей системи. Оскільки ми припускаємо, що нічого про систему не змінюється на кроці збурень та ізоляції, то ентропія збуреної, ізольованої, гіпотетичної системи залишається такою ж, як і у вихідної системи рівноваги.

Малюнок 2. Спонтанні і оборотні процеси, що з'єднують однакові стану рівноваги

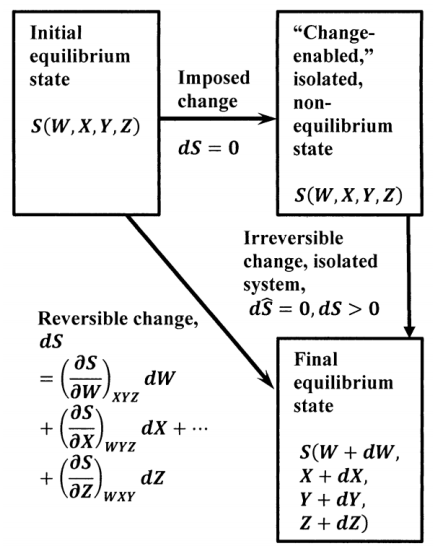
На малюнку 2 показані ентропії для трьох станів циклу, який включає модель Ле Шательє для змін. Ентропія вихідної системи рівноваги є\(S\left(W,X,Y,Z\right)\) і система кінцевої рівноваги є\(S\left(W+dW,X+dX,Y+dY,Z+dZ\right)\). Однаковий кінцевий стан рівноваги досягається як незворотним переходом від гіпотетичного стану, що підтримується змінами, так і оборотним переходом від початкового стану рівноваги. Оскільки ентропія є функцією стану, її зміна навколо цього циклу повинна дорівнювати нулю. Отже, інкрементні зміни\(dW\),\(dX\)\(dY\), і\(dZ\) які відбуваються в термодинамічних змінних повинні задовольняти нерівність

\[{\left(\frac{\partial S}{\partial W}\right)}_{XYZ}dW+{\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX+{\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY +{\left(\frac{\partial S}{\partial Z}\right)}_{WXY}dZ>0\]

Застосування цієї нерівності до гіпотетичної, що підтримується змінами, ізольована система може розглядатися як математичний вираз принципу Ле Шательє. Щоб побачити це чіткіше, припустимо, що ми здатні тримати\(W\) і\(Z\) постійно. Ми припускаємо, що нав'язана зміна вимагає, щоб остаточне значення\(X\) бути\(X+dX\). Щоб система залишалася в рівновазі, що залишилася змінна\(Y\), повинна змінитися на величину\(dY\), яка задовольняє цю нерівність. Тобто, щоб досягти нового стану рівноваги, зміна\(Y\) повинна задовольнити

\[{\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX+{\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY>0\]

У цій моделі змінні\(X\) і\(Y\) привід ентропії змінюються, оскільки гіпотетична система рухається до свого нового положення рівноваги. Нав'язана зміна\(X\) змінює ентропію системи по

\[dS_{imposed}={\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX\]

Оскільки ефект нав'язаної зміни полягає в тому, щоб відігнати систему від початкового положення рівноваги, ми маємо\(dS_{imposed}<0\). Відповідь системи змінює ентропію системи на

\[dS_{response}={\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY\]

Ми маємо\(dS_{response}>-dS_{imposed}>0\), щоб ми могли обґрунтовано описати відповідь\(dY\), яка робить\(dS_{response}>0\), як зміна, яка виступає проти нав'язаних змін\(dX\), що робить\(dS_{imposed}<0\).

Застосування принципу Ле Шательє - це щось на зразок мистецтва. Центральним у цьому мистецтві є здатність розробляти гіпотетичний, що підтримується змінами, ізольований, нерівноважний стан, який є хорошою моделлю для початкового стану спонтанного процесу. У розділі 6.6 ми використовуємо якісні аргументи для застосування принципу Ле Шательє до рівноваги пара — рідина. Щоб зв'язати ці якісні аргументи з розробленою нами математичною моделлю, розглянемо експеримент геданкена, зображений на малюнку 3. Ми припускаємо, що початкова система рівноваги містить рідину і пари чистої речовини при тиску\(P\), і температурі,\(T\). Ми уявляємо, що можемо створити гіпотетичну ізольовану систему, нав'язавши ступінчасту зміну прикладеного тиску без зміни тиску системи.

Малюнок 3. Спонтанні і оборотні процеси, що з'єднують однакові стану рівноваги рідина-пара.

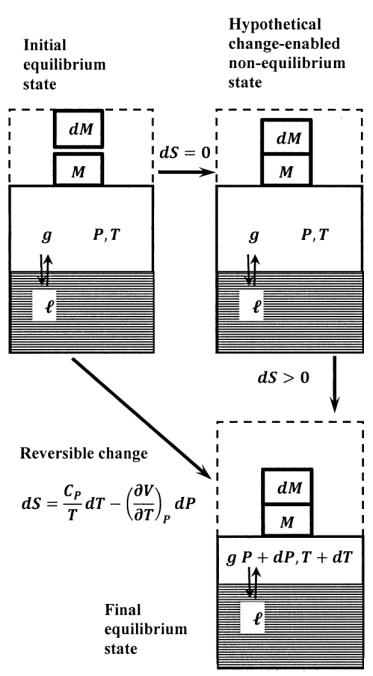
Для моделювання збурень тиску розглянемо суміш рідина-пара як підсистему, яка укладена у вертикальний циліндр, герметичний поршнем без тертя. А маса\(M\), спирається зверху на поршень. Для наведених цілей ми вважаємо цю масу частиною другої підсистеми. Гравітаційна сила на цю масу створює тиск, що додається до суміші рідина-пара. Оскільки це рівноважний стан речовини, це прикладене тиск дорівнює тиску підсистеми рідина—пара.\(P\) Невелика маса,\(dM\), також входить до складу другої підсистеми. У цьому початковому рівноважному стані системи ця менша маса певним чином підтримується, так що вона не сприяє прикладеному тиску. Ми припускаємо, що поршень є ідеальним теплоізолятором, так що між двома підсистемами не можна обмінюватися теплом.

Як намальовано на малюнку 3, ми створюємо гіпотетичну систему з підтримкою змін, переміщуючи меншу масу так, щоб вона теж спиралася на верхню частину поршня. Відразу після цього ми повністю ізолюємо систему від решти Всесвіту. Припускаємо, що прикладається тиск миттєво збільшується до\(P+dP\). Однак, оскільки підсистема рідина—пара незмінна, ми припускаємо, що тиск, ентропія та всі інші термодинамічні властивості підсистеми рідина—пара залишаються незмінними в цьому гіпотетичному стані. Система не знаходиться в рівновазі в цьому гіпотетичному стані, тому що прикладається тиск не дорівнює тиску підсистеми рідина-пара. Може статися спонтанне перехід на новий стан рівноваги. Тому що система ізольована,\(\Delta \hat{S}=0\). Тому у нас є\(\Delta S>0\). Кінцева рівноважна температура становить\(T+dT\).

Маючи тиск і температуру як незалежні змінні, ця модель для принципу Ле Шательє породжує наступну математичну вимогу:

\[dS=T^{-1}{\left({\partial H}/{\partial T}\right)}_PdT-{\left({\partial V}/{\partial T}\right)}_PdP>0.\]

Ми це знаємо\(T\)\({\left({\partial H}/{\partial T}\right)}_P\), і\({\left({\partial V}/{\partial T}\right)}_P\) є позитивними. Тому ми можемо переставити нерівність, щоб знайти

\[dT>T\left[{{\left(\frac{\partial V}{\partial T}\right)}_P}/{{\left(\frac{\partial H}{\partial T}\right)}_P}\right]dP\]

Якщо ми маємо\(dP>0\), то випливає, що\(dT>0\); тобто температура рівноваги рідина-пара збільшується з тиском.