9.7: Зміни ентропії для спонтанного процесу в ізольованій системі

У розділі 9.6 ми розглядаємо зміни ентропії в системі та її оточенні, коли процес є оборотним. Розглянемо зараз діаметрально протилежну ситуацію, при якій ізольована система зазнає спонтанної зміни. З ентропійного твердження другого закону ми знаємо, як змінюється ентропія цієї системи та її оточення. Оскільки система ізольована, ніяких змін в оточенні не відбувається. Таким чином,\(\Delta \hat{S}=0\); і з тих пір\(\Delta S+\Delta \hat{S}>0\), у нас є\(\Delta S>0\).

Спробуємо розробити ці висновки з машинного положення другого закону. Оскільки процес відбувається необоротно, ми не можемо використовувати тепло процесу, щоб знайти зміну ентропії для системи. Ми можемо обчислити зміну ентропії для процесу з визначального рівняння, лише якщо процес є оборотним. Однак ентропія - це функція стану; використовуючи фігуру мови, яку ми вводимо в Розділі 7.21, ми можемо знайти зміну ентропії для спонтанного процесу, оцінюючи\(\Delta S\) по другому та оборотному шляху, який з'єднує ті ж початкові та кінцеві стани.

Малюнок 7. Цикл, що включає в себе спонтанний процес в ізольованій системі.

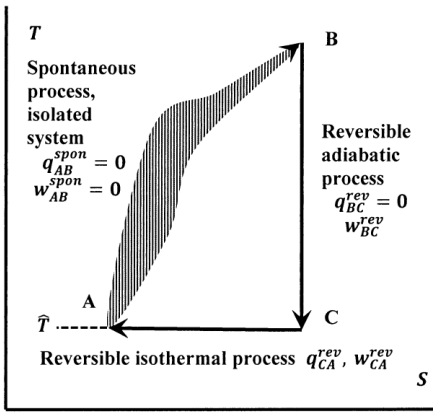
На малюнку 7 ці шляхи побудовані в температурно-ентропійному просторі. Перехід від стану A до стану B відбувається необоротно, і тому він не обов'язково відповідає шляху, який ми можемо вказати на цій діаграмі. Пунктирна лінія, намальована для цього переходу, повинна нагадувати нам про цей факт. Ми можемо легко розробити оборотний шлях від B назад до А. По-перше, ми оборотно і адіабатично повертаємо температуру системи до її початкового значення\(\hat{T}\). На цьому кроці система дійсно працює над оточенням, або навпаки. Система досягає точки С на схемі. Потім ми оборотно і ізотермічно додаємо або видаляємо тепло з системи, щоб повернутися до початкового стану в точці А. Щоб передача тепла була оборотною, ми повинні мати\(T=\hat{T}\) для цього кроку. Значить, кінцева (і початкова) температура системи в точці А дорівнює температурі оточення. Оборотний шлях\(B\to C\to A\) повинен існувати, оскільки теорема плитки стверджує, що адіабати (вертикальні лінії) та ізотерми (горизонтальні лінії) плитку\(T--S\) -площину довільно щільно.

Взяте буквально, цей опис стану А є непослідовним. Ми припускаємо, що початковий стан А здатний до спонтанних змін; отже, це не може бути рівноважним станом. Ми припускаємо, що кінцевий стан А досягається оборотним процесом; отже, він повинен бути рівноважним станом. Ми переходимо до цього протиріччя шляхом уточнення нашого визначення початкового стану. Кінцевий стан А - це рівноважний стан з чітко визначеними функціями стану. Ми маємо на увазі, що ці кінцеві значення рівноваги також характеризують початковий нерівноважний стан. Очевидно, що початковий стан А, який ми маємо на увазі, є гіпотетичним станом. Це гіпотетичний стан наближає стан реальної системи, яка зазнає спонтанних змін. Викликаючи цей гіпотетичний початковий стан, ми усуваємо протиріччя між нашими описами початкового стану А та кінцевого стану А. Враховуючи реальну систему, яка зазнає спонтанної зміни, ми повинні знайти наближені значення функцій стану реальної системи шляхом знаходження рівноваги - або квазірівноваги— система, яка адекватно моделює початковий стан спонтанно мінливої системи.

У розробці нижче ми не ставимо жодних обмежень на характер системи або спонтанний процес. Припускається, що функції стану будь-якого гіпотетичного початкового стану А можуть бути адекватно апроксимовані деякою моделлю рівноважного стану. Однак перш ніж розглядати загальний аргумент, покажемо, як ці умови можуть бути дотримані для іншої конкретної системи. Розглянемо посудину, інтер'єр якого розділений перегородкою. Справжній газ чистої речовини займає простір з одного боку перегородки. Простір з іншого боку перегородки евакуюється. Припускаємо, що ця посудина ізольована. Реальний газ знаходиться в рівновазі. Ми можемо виміряти його функції стану, включаючи тиск, об'єм та температуру. Тепер припустимо, що ми проколюємо перегородку. Як тільки ми це робимо, газ спонтанно розширюється, щоб заповнити всю посудину, досягаючи нового положення рівноваги, при новому тиску, об'ємі та температурі. Газ піддається вільному розширенню, як визначено в розділі 7.17.

У той момент, коли розділ проколюється, система стає здатною піддаватися мимовільній зміні. У цьому гіпотетичному початковому стані до того, як через отвір пройде будь-яка значна кількість газу, ні фактичний стан газу, ні значення його функцій стану. Після розширення до нового стану рівноваги початковий стан може бути відновлено оборотними процесами адіабатичного стиснення та ізотермічного регулювання об'єму. (Задачі 13 і 14 в главі 10 стосуються зміни енергії та ентропії ідеальних і реальних газів навколо циклу, в якому спонтанне розширення в ізольованій системі супроводжується оборотним відновленням початкового стану.)

Повертаючись до загального циклу, зображеному на малюнку 7, ми бачимо, що на окремих етапах існують деякі важливі умови по тепловому і робочому термінам. Оскільки система ізольована під час переходу від A до B, вона не обмінюється теплом або працює з оточенням на цьому кроці:\(q^{spon}_{AB}=w^{spon}_{AB}=0\). Для оборотного адіабатичного переходу від B до C,\(d_{BC}q^{rev}=0\) в кожній інкрементній частині шляху. Перехід від C до A відбувається оборотно і ізотермічно; дозволяючи теплоті цього кроку бути\(q^{rev}_{CA}\), зміни ентропії для цих оборотних кроків є, з визначального рівняння,

\[{\Delta }_{BC}S=\int^{T_C}_{T_B}{\frac{d_{BC}q^{rev}}{T}}=0\]і\[{\Delta }_{CA}S=\frac{q^{rev}_{CA}}{\hat{T}}\]

Зміни енергії та ентропії навколо цього циклу повинні бути нульовими, незалежно від того, чи відбуваються окремі кроки оборотно або необоротно. У нас є

\[\Delta E=q^{spon}_{AB}+w^{spon}_{AB}+q^{rev}_{BC}+w^{rev}_{BC}+q^{rev}_{CA}+w^{rev}_{CA}=q^{rev}_{CA}+w^{rev}_{BC}+w^{rev}_{CA}=0\]і

\[\Delta S={\Delta }_{AB}S+{\Delta }_{BC}S+{\Delta }_{CA}S ={\Delta }_{AB}S+{q^{rev}_{CA}}/{\hat{T}}=0\]

Ми хочемо проаналізувати цей цикл, використовуючи машинне твердження другого закону. У нас є\(w^{rev}_{BC}=-{\hat{w}}^{rev}_{BC}\)\(w^{rev}_{CA}=-{\hat{w}}^{rev}_{CA}\), і\(q^{rev}_{CA}=-{\hat{q}}^{rev}_{CA}\). Припустимо, що система робить чисту роботу над навколишнім середовищем, оскільки цей цикл проходить так, що\({\hat{w}}^{rev}_{BC}+{\hat{w}}^{rev}_{CA}>0\). Потім,

\[-\left({\hat{w}}^{rev}_{BC}+{\hat{w}}^{rev}_{CA}\right)=w^{rev}_{BC}+w^{rev}_{CA}<0\]

і з цього випливає\(q^{rev}_{CA}>0\). Система обмінюється теплом з навколишнім середовищем лише за один етап цього процесу. На цьому етапі система витягує певну кількість тепла з резервуара в околицях. Температура цього водойми залишається постійною на\(\hat{T}\) протязі всього процесу. Тепло, що виділяється системою, повністю перетворюється в роботу. Цей результат суперечить машинному твердженню другого закону. Отже,\(w^{rev}_{BC}+w^{rev}_{CA}<0\) є помилковим; з цього випливає, що

\[w^{rev}_{BC}+w^{rev}_{CA}\ge 0\]

і що\[q^{rev}_{CA}\le 0\]

Для зміни ентропії спонтанного процесу в ізольованій системі ми маємо

\[{\Delta }_{AB}S=-{q^{rev}_{CA}}/{\hat{T}}\ge 0\]

Тепер ми представляємо передумову, що\(q^{rev}_{CA}\neq 0\). Якщо це правда, зміна ентропії спонтанного процесу в ізольованій системі стає

\[{\Delta }_{AB}S>0\]

(Зворотне також вірно; тобто\({\Delta }_{AB}S>0\) означає, що\(q^{rev}_{CA}\neq 0\).) Передумова,\(q^{rev}_{CA}\neq 0\) яка не залежить від машинного твердження другого закону, який вимагає лише цього\(q^{rev}_{CA}\le 0\), як ми щойно продемонстрували. Він також не залежить від першого закону, який вимагає тільки цього\(q^{rev}_{CA}=-w^{rev}_{BC}-w^{rev}_{CA}\). Якщо\(q^{rev}_{CA}\neq 0\), можна зробити висновок, що для спонтанного процесу в ізольованій системі ми повинні мати\(w_{BC}+w_{CA}>0\) і\(q^{rev}_{CA}<0\). Ці умови відповідають виконанню роботи над системою та виявленню того, що тепло виділяється системою. Заперечень проти цього немає, можливо кількісно перетворювати механічну енергію в теплову. Висновки, які\(q^{rev}_{CA}<0\) і\({\Delta }_{AB}S>0\) мають важливі наслідки; розглянемо їх нижче. По-перше, однак, ми розглядаємо лінію думки, яка змушує нас зробити висновок, що\(q^{rev}_{CA}\neq 0\) і, отже, це\(q^{rev}_{CA}<0\) повинно бути правдою.

Тому що\(q_{AB}=0\) і\(w_{AB}=0\), у нас є\({\ E}_A=E_B\). Система може бути взята з стану А в стан B оборотним процесом А\(\to C\to B\). Вище ми бачимо, що якщо\(q^{rev}_{CA}=0\), у нас є\({\ S}_A=S_B\). У § 6-10 ми вводимо теорему Дюхема, яка стверджує, що двох термодинамічних змінних достатньо для визначення стану замкнутої оборотної системи, в якій можлива лише робота тиск-об'єм. Ми дали доказ теореми Дюхема, коли дві змінні вибираються з числа змінних тиску, температури та складу, що описують систему. Ми уникали уточнення, чи можна використовувати інші пари змінних. Якщо припустити тепер, що вказівки змінних енергія і ентропія завжди достатньо для зазначення стану такої системи, то випливає, що стани A і B фактично повинні бути одним і тим же станом. (У § 14, і більш детально в главі 10, ми бачимо, що перший закон і наше засноване на ентропії твердження другого закону дійсно означають, що визначення енергії та ентропії визначає стан замкнутої оборотної системи, в якій можлива лише робота тиску - об'єму.)

Якщо стан A і стан B є одним і тим же станом; тобто якщо державні функції держави А такі ж, як і у стану B, то безглуздо говорити про те, що існує спонтанний процес, який перетворює стан А в стан Б. Тому, якщо A може бути перетворений в B при спонтанному процесі в ізольованій системі, він повинен бути що\(q^{rev}_{CA}\neq 0\). Тобто,

\[\left[\left(q^{rev}_{CA}=0\right)\Rightarrow \sim \left(\mathrm{A\ can\ go\ to\ B\ spontaneously}\right)\right]\]\[\Rightarrow \left[\left(A\ \mathrm{can\ go\ to\ B\ spontaneously}\right)\Rightarrow \left(q^{rev}_{CA}\neq 0\right)\right]\]

З машинного твердження другого закону знаходимо\({\Delta }_{AB}S=-{q^{rev}_{CA}}/{\hat{T}}\ge 0\). Коли ми доповнимо цей висновок нашим висновком Духема, заснованим на теоремах\(q^{rev}_{CA}\neq 0\), ми можемо зробити висновок, що\(\Delta S>0\) для будь-якого спонтанного процесу в будь-якій ізольованій системі. Оскільки система ізольована, ми маємо\(\hat{q}=0\), і\(\Delta \hat{S}=0\). Для будь-якого спонтанного процесу в будь-якій ізольованій системі ми маємо

\[\Delta S_{universe}=\Delta S+\Delta \hat{S}>0.\]

Можна також зробити висновок, що зворотне вірно; тобто якщо\({\Delta }_{AB}S=S_B-S_A>0\) для процесу, в якому ізольована система переходить від стану А до стану B, процес повинен бути спонтанним. Оскільки будь-який процес, що відбувається в ізольованій системі, повинен бути спонтанним процесом, необхідно лише показати, що\({\Delta }_{AB}S>0\) має на увазі, що стан В відрізняється від стану А. Оскільки ентропія є функцією стану,\(S_B-S_A>0\) вимагає, щоб стан B відрізнявся від стану А.

Жоден наш аргумент не залежить від величини зміни, що відбувається. Очевидно, що та сама нерівність повинна описувати кожну інкрементну частину будь-якого спонтанного процесу; інакше ми могли б визначити поступову спонтанну зміну, для якої було б порушено машинне твердження другого закону. Для кожної інкрементної частини будь-якої спонтанної зміни в будь-якій ізольованій системі ми маємо\(dS>0\) і

\[dS_{universe}=dS+d\hat{S}>0.\]

Це надзвичайно важливі результати; ми досліджуємо їх наслідки нижче. Однак, перш ніж це зробити, давайте ще раз розглянемо систему, в якій можлива лише робота тиску - об'єму. Існує альтернативний спосіб висловити думку про те, що така система ізольована. Оскільки ізольована система ніяк не може взаємодіяти зі своїм оточенням, вона не може обмінюватися енергією зі своїм оточенням. Його енергія повинна бути постійною. Оскільки він не може обмінюватися тиском - об'ємом роботи, його обсяг повинен бути постійним. Значить, ізоляція має на увазі постійне\(E\) і\(V\). Якщо можлива лише робота з тиском - об'ємом, зворотне має бути істинним; тобто, якщо можлива лише робота над тиском - об'ємом, постійна енергія та об'єм означають, що між системою та її оточенням не існує взаємодій. Тому постійні\(E\) і\(V\) мають на увазі, що система ізольована, і це повинно бути правдою\(\Delta \hat{S}=0\). При цьому спонтанний процес, при якому\(E\) і\(V\) є постійними, повинен супроводжуватися збільшенням ентропії системи. (Якщо\(V\) постійний і можливий лише тиск - об'ємна робота, процес не передбачає жодної роботи.) У нас є критерій спонтанної зміни:

\[{\left(\Delta S\right)}_{EV}>0\](спонтанний процес, тільки тиск - об'ємна робота)

де індекси вказують на те, що енергія і обсяг системи постійні. (У розділі 9.21 ми дійдемо до цього висновку іншим аргументом.)