9.5: Теорема плитки та шляхи циклічного процесу в інших просторах

Ми розглядаємо теорему плитки як узагальнення з досвіду, так само як машинне твердження другого закону є таким узагальненням. Розглянемо види знайомих спостережень, з яких зробимо висновок, що кожен рівноважний стан будь-якої системи перетинається одним і тільки одним адіабатом і однією і тільки однією ізотермою.

Коли можлива лише робота «тиск — об'єм», кожна точка тиску — об'єму визначає унікальний стан рівноваги системи. Оскільки температура є функцією стану, то температура цього стану має одне і тільки одне значення. Коли можлива інша форма роботи, в кожній\({\mathit{\Phi}}_i{-\theta }_i\) точці вказується унікальний стан, для якого температура має одне і тільки одне значення. З досвіду ми знаємо, що ми можемо виробляти новий стан системи, при тій же температурі, обмінюючись теплом і працювати з ним узгоджено. Ми можемо зробити цю зміну стану довільно малим, так що послідовні рівноважні стани з однаковою температурою довільно близькі один до одного. Ця послідовність довільно близьких рівноважних станів є ізотермою. Тому хоча б одна ізотерма перетинає будь-який стан рівноваги. Таких ізотерм не може бути двох. Якби було дві ізотерми, система мала б дві температури, порушуючи принцип, що температура є функцією стану.

У адіабатичному процесі система обмінюється енергією як робота, але не як тепло. З досвіду ми знаємо, що ми можемо здійснити таку зміну за допомогою будь-якої оборотної системи. В результаті виходить новий стан рівноваги. Коли ми робимо приріст роботи довільно малим, новий стан рівноваги довільно близький до початкового стану. Послідовні обміни довільно малих приростів роботи виробляють послідовні стани рівноваги, які довільно близькі один до одного. Ця послідовність довільно близьких рівноважних станів є адиабатом.

Якби однаковий стан системи може бути досягнутий двома оборотними адіабатами, що включають однакову форму роботи, ефект виконання заданого обсягу цієї роботи на рівноважну систему не був би унікальним. З того ж початкового стану два оборотні адіабатичні експерименти могли б зробити однакову кількість тієї ж роботи і досягти різних кінцевих станів системи. Наприклад, у двох різних експериментах ми могли б підняти вагу оборотно з тієї ж початкової висоти, виконати однакову кількість роботи в кожному експерименті і виявити, що остаточне піднесення ваги відрізняється. Будь-який такий результат суперечить спостереженням, які лежать в основі наших уявлень про оборотні процеси.

Більш конкретно, існування двох адіабатів через задану точку, в будь-якому\({\mathit{\Phi}}_i{-\theta }_i\) просторі, порушує машинне твердження другого закону. Два таких адіабата обов'язково перетинають загальну ізотерму. Шляхом по одному адіабату, ізотермі і другому адиабату був би циклом, який відновив систему до початкового стану. Цей шлях буде охоплювати скінченну область. Пройдений у відповідному напрямку, цикл виробляв би роботу в околицях. Згідно з першим законом, система буде приймати тепло, коли вона проходить ізотерму. Система обмінювалася теплом з навколишнім середовищем при одній температурі і виробляла позитивну роботу в оточенні, порушуючи тим самим заяву на основі машини.

Якщо адіабатичний процес, який з'єднує два стани A і B, є оборотним, ми бачимо, що система йде тим самим шляхом, в протилежних напрямках, коли вона працює від A до B, як це робить, коли робота виконується над нею, як вона йде від B до A.

З іншої точки зору можна сказати, що теорема укладання плитки є наслідком наших припущень про оборотні процеси. Наша концепція оборотного процесу полягає в тому, що енергія, тиск, температура і об'єм є безперервними функціями стану, з безперервними похідними. Те, що існує одна і тільки одна ізотерма для кожного стану, еквівалентно припущенню, що температура - це безперервна (однозначна) функція стану системи. Те, що існує один і тільки один адіабат для кожного стану, еквівалентно припущенню\({\left({\partial E}/{\partial V}\right)}_{T,{\theta }_1}\), що\({\left({\partial E}/{\partial {\theta }_i}\right)}_{T,V,{\theta }_{m\neq i}}\), або взагалі, є безперервною однозначною функцією стану системи.

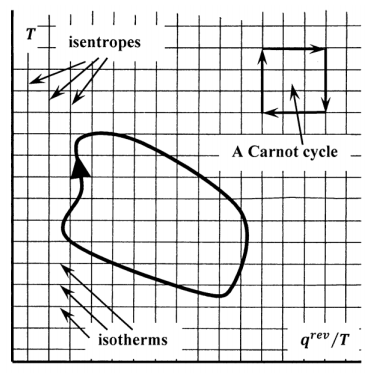
Маючи на увазі ці ідеї, давайте тепер помітимо, що будь-який оборотний цикл може бути описаний замкнутим шляхом у просторі, координати якого є\(T\) і\({q^{rev}}/{T}\) (ентропія). На малюнку 5 ми накидаємо цей простір з\({q^{rev}}/{T}\) на абсцисі; тоді ізотерма - горизонтальна лінія, а лінія постійної ентропії (ізентроп) - вертикальна. Реверсивний цикл Карно - це замкнутий прямокутник, і площа цього прямокутника відповідає оборотній роботі, виконаної системою над його оточенням за один цикл. Будь-який стан рівноваги системи відповідає певній точці в цьому просторі. Будь-який замкнутий шлях може бути викладений довільно щільно ізотермами і ізентропами. Будь-який оборотний цикл, що передбачає будь-яку форму роботи, представлений замкнутим шляхом в цьому просторі. Малюнок 5 є альтернативною ілюстрацією аргументу, який ми робимо в розділі 9.4. Шляхи в цьому просторі не залежать від виду виконаної роботи, підкріплюючи висновок, що\(\oint{dq^{rev}/T=0}\) для оборотного циклу Карно виробляють будь-яку форму роботи. Той факт, що циклічний процес відповідає замкнутому шляху в цьому просторі, рівносильно тому, що ентропія - це функція стану.

Малюнок 5. Оборотний цикл описується за допомогою координат\(T\) і\(q^{rev}/T\).

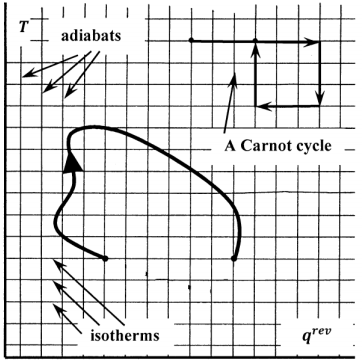
Щоб оцінити цей аспект шляху циклічного процесу в\(T-q^{rev}/{T}\) просторі, опишемо шлях того ж процесу в просторі, координати якого є\(T\) і\(q^{rev}\). З\(q^{rev}\) на абсцисах ізотерми - це знову горизонтальні лінії, а адіабати - вертикальні. У цьому просторі оборотний цикл Карно не починається і не закінчується в одній точці. Шляхи не закриті. Аналогічно зображення довільного оборотного циклу не є замкнутою фігурою. Див. Рисунок 6. Різниця між уявленнями оборотного циклічного процесу в цих двох просторах графічно ілюструє той факт, що ентропія є функцією стану, а тепло - ні.

Малюнок 6. Оборотний цикл, описаний за допомогою\(T\) та\(q^{rev}\)