15.4: Вирази функції кореляції часу для швидкості переходу
- Page ID
- 22233
Вираз E1 першого порядку «золоте правило» для швидкостей фотонно-індукованих переходів може бути перероблений у форму, в якій легко вводяться певні конкретні фізичні моделі та легко отримати уявлення. Крім того, за допомогою так званих рівноважних усереднених часових кореляційних функцій можна отримати вирази швидкості, відповідні великій кількості молекул, які існують у розподілі початкових станів (наприклад, для молекул, які займають багато можливих обертальних і, можливо, декількох коливальних рівнів у приміщенні. температура).
Стан до стану швидкість поглинання або викидів енергії
Для початку вираз, отримане раніше
\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2}\right) g(\omega_{f,i}) | \textbf{E}_0 \cdot{\langle} \phi_f | \mu | \Phi_i \rangle |^2, \]
що підходить для переходів між певним початковим станом\(\Phi_i \) і конкретним кінцевим станом\(\Phi_f\), переписується як
\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2}\right) \int g( \omega ) | \textbf{E}_0 \cdot{\langle} \phi_i | \mu | \phi_i \rangle |^2 \delta (\omega_{f,i} - \omega )\text{ d}\omega . \]
Тут\(\delta (\omega_{f,i} - \omega )\) функція використовується для конкретного забезпечення «резонансної умови», що призвело до залежної від часу обробки збурень, наведеної в главі 14; він стверджує, що частота фотонів\(\omega\) повинна бути резонансною з частотою переходу\(\omega_{f,i}\). Слід зазначити, що, дозволяючи\(\omega\) працювати над позитивними та негативними значеннями, поглинання фотонів (з\(\omega_{f,i}\) позитивним, а отже, і w позитивним) та випадок стимульованого випромінювання (з\(\omega_{f,i}\) негативним і, отже,\(\omega\) негативним) включаються в цей вираз (до тих пір, поки g ( \(\omega\)) визначається як g (|\(\omega\) |) так що негативні\(\omega\) внески множаться на інтенсивність джерела світла при відповідному позитивному\(\omega\) значенні).
Наступний інтегральний ідентифікатор може бути використаний для заміни\(\delta\) -функції:
\[ \delta (\omega_{f,i} - \omega ) = \dfrac{1}{2\pi} \int\limits_{-\infty}^{\infty} e^{i(\omega_{f,i} - \omega )t} \text{ dt} \]
формою, яка більше піддається подальшому розвитку. Потім швидкість переходу від стану до стану стає:
\[ R_{i,f} = \left(\dfrac{1}{\hbar}\right) \int g(\omega ) | \textbf{E}_0 \cdot{\langle}\phi_f | \mu | \phi_i \rangle |^2 \int\limits_{-\infty}^{\infty}e^{i(\omega_{f,i} - \omega)t} \text{ dt d}\omega . \]
Усереднення над рівновагою населення Больцмана початкових держав
Якщо цей вираз потім помножити на рівноважну ймовірність\(\rho_i\) того, що молекула знаходиться в стані\(\Phi_i\) і підсумовується над усіма такими початковими станами і підсумовується по всіх кінцевих станах,\(\Phi_f\) які можуть бути досягнуті\(\Phi_i\) з фотонами енергії\(\hbar \omega\), то Отримано рівноважну усереднену швидкість поглинання фотонів молекулярним зразком:
\[ R_{\text{eq.ave.}} = \left( \dfrac{1}{\hbar^2} \right) \sum\limits_{i,f} \rho_i \]
\[ \int g(\omega ) | \textbf{E}_0 \cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \int\limits_{-\infty}^{\infty} e^{i(\omega_{f,i} - \omega )t} \text{dt d}\omega . \]
Цей вираз доречно для ансамблю молекул, які можуть перебувати в різних початкових станах\(\Phi_i\) з ймовірностями\(\rho_i\). Відповідний результат для переходів, які походять у певному стані (\(\Phi_i\)), але в кінцевому підсумку в будь-якому з «дозволених» (за енергією та правилами вибору) кінцевих станів говорить:
\[ R_{\text{state i.}} = \left( \dfrac{1}{\hbar^2} \right) \sum\limits_f \int g(\omega ) | \textbf{E}_0 \cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \]
\[ \int\limits_{-\infty}^{\infty} e^{i(\omega_{f,i} - \omega )t}\text{ dtd}\omega . \]
Для канонічного ансамблю, в якому вказується кількість молекул, температура, і обсяг системи,\(\rho_i\) набуває вигляду:
\[ \phi_i = \dfrac{g_i}{Q}e^{-\dfrac{E_i^0}{kT}} \]
де Q - канонічна функція поділу молекул і\(g_i\) є виродженням стану, енергія\(\Phi_i\) якого\(\text{E}_i^0.\)
У вищенаведеному\(\text{R}_{\text{eq.ave.}}\) виразі for відбувається подвійна сума. Виписуючи елементи, які фігурують в цій сумі докладно, можна знайти:
\[ \sum\limits_{i,f} \phi_i \textbf{E}_0 \cdot{\langle} \Phi_i | \mu | \Phi_f \rangle \textbf{E}_0 \cdot{\langle}\Phi_f | \mu | \Phi_i \rangle e^{i(\omega_{f,i})t}. \]
У ситуаціях, коли людина зацікавлена в розробці виразу для інтенсивності, що виникає при переходах до всіх дозволених кінцевих станів, сума над цими кінцевими станами може бути здійснена явно шляхом першого написання
\[ \langle \Phi_f | \mu | \Phi_i \rangle e^{i(\omega_{f,i})t} = \langle \Phi_f | e^{\dfrac{iHt}{\hbar}} \mu e^{-\dfrac{iHt}{\hbar}} | \Phi_i \rangle \]
а потім використовуючи той факт, що множина станів {\(\Phi_k\)} повні і, отже, підкоряються
\[ \sum\limits_k | \Phi_k \rangle \langle \Phi_k | = 1.\]
Результат використання цих тотожностей, а також визначення Гейзенберга часової залежності дипольного оператора
\[ \mu (t) = e^{\dfrac{iHt}{\hbar}} \mu e^{-\dfrac{iHt}{\hbar}}, \]
це:
\[ \sum\limits_i \rho_i \langle \Phi | \textbf{E}_0 \cdot{\mu} \textbf{E}_0\cdot{\mu}(t) | \Phi_i \rangle . \]
У цій формі кажуть, що залежність часу була зменшена до залежності рівноважної усередненої (n.b., a\( \sum\limits_i \rho_i \langle \Phi_i | | \Phi_i \rangle \)) часової кореляційної функції, що включає компонент дипольного оператора уздовж зовнішнього електричного поля при t = 0 (\(\textbf{E}_0\cdot{\mu}\)) і цей компонент в інший час \( t(\textbf{E}_0\cdot{\mu}(t))\).
Випромінювання та поглинання фотонів
Якщо\(\omega_{f,i}\) позитивний (тобто у випадку поглинання фотонів), вищевказаний вираз дасть ненульовий внесок при множенні\(e^{-i \omega t}\) та інтеграції над додатними\(\omega \) значеннями. Якщо\(\omega_{f,i}\) негативний (як для стимульованого випромінювання фотонів), цей вираз буде сприяти, знову ж таки, при множенні на\(e^{-i\omega t}\), для негативних\(\omega \) -значень. В останній ситуації\(\rho_i\) - це рівноважна ймовірність знаходження молекули в (збудженому) стані, з якого буде відбуватися емісія; ця ймовірність може бути пов'язана з ймовірністю нижчого стану\(\rho_f\) шляхом
\[ \rho_{\text{excited}} = \rho_{\text{lower}} e^{-\dfrac{(\text{E}^0_{\text{excited}} - \text{E}^0_{\text{lower}})}{kT}} \]
\[ = \rho_{\text{lower}}e^{-\dfrac{\hbar \omega}{kT}}. \]
У цій формі важливо усвідомлювати, що збуджені та нижчі стани трактуються як окремі стани, а не як рівні, які можуть містити вироджений набір станів.
Випадки поглинання та випромінювання можуть бути об'єднані в єдиний чистий вираз для швидкості поглинання фотонів, визнаючи, що останній процес призводить до виробництва фотонів, і, таким чином, повинен бути введений з негативним знаком. Отриманий вираз для чистої швидкості зменшення фотонів становить:
\[ \text{R}_{\text{eq.ave.net}} = \left( \dfrac{1}{\hbar^2} \right) \sum\limits_i \rho_i \left( 1 - e^{-\dfrac{\hbar \omega}{kT}} \right) \]
\[ \iint g(\omega ) \langle \Phi_i | (\textbf{E}_0 \cdot{\mu} ) \textbf{E}_0 \cdot{\mu}(t) | \Phi_i \rangle e^{-i\omega t} \,d\omega \,dt. \]
Лінійна форма та часові кореляційні функції
Тепер це умовність ввести так звану функцію «форма лінії»\(I(\omega)\):
\[ I(\omega ) = \sum\limits_i \rho_i \int \langle \Phi_i | (\textbf{E}_0 \cdot{\mu}) \textbf{E}_0\cdot{\mu} (t) | \Phi_i \rangle e^{-i\omega t}\, dt \]
в плані яких швидкість поглинання чистого фотонів становить
\[ \text{R}_{\text{eq.ave.net}} = \left( \dfrac{1}{\hbar^2} \right) \left( 1 -e^{-\hbar \omega/kT}\right) \int g(\omega )I(\omega ) \text{ d}\omega . \]
Як зазначено вище, функція
\[ \text{C}(t) = \sum\limits_i \rho_i \langle \Phi_i | \textbf{E}_0 \cdot{\mu} ) \textbf{E}_0\cdot{\mu}(t) | \Phi_i \rangle \]
називається рівноважною усередненою часовою кореляційною функцією компонента електричного дипольного оператора уздовж напрямку зовнішнього електричного поля\(\textbf{E}_0\). Його перетворення Фур'є є\(I(\omega)\) функцією форми спектральної лінії. Згортка\(I(\omega)\) з функцією джерела світла (\ g (\ omega\)), помножена на\(\left(1 - e^{-\frac{h \omega}{kT}} \right)\) поправку для стимульованого випромінювання фотонів, дає чисту швидкість поглинання фотонів.
Обертальний, поступальний та вібраційний внесок у кореляційну функцію
Щоб застосувати механізм часової кореляційної функції до кожного конкретного виду спектроскопічного переходу, продовжується наступним чином:
Чисті обертальні переходи
Для чисто обертальних переходів початкове і кінцеве електронне і коливальне стани однакові. Крім того, електронний і коливальний стани не підсумовуються в аналозі вищезазначеної розробки, оскільки зацікавлений в отриманні виразу для конкретної форми лінії\( \chi_{\text{iv}} \psi_{\text{ie}} \rightarrow \chi_{\text{fv}} \psi_{\text{fe}} \) електронно-коливального переходу. Як результат, сума над кінцевими станами, що містяться у виразі (див. Раніше)
\[ \sum\limits_{\text{i,f}} \rho_i \textbf{E}_0 \cdot{\langle} \Phi_{\text{i}} | \mu | \Phi_{\text{f}} \rangle \textbf{E}_0 \cdot{\langle} \Phi_{\text{f}} | \mu (t) | \Phi_{\text{i}} \rangle e^{i(\omega_{\text{f,i}})t} \]
застосовується тільки до підсумовування над кінцевими обертальними станами. Більш детально це можна показати наступним чином:
\[ \sum\limits_{\text{i,f}} \rho_{\text{i}} \textbf{E}_0 \cdot{\langle}\Phi_{\text{i}} | \mu | \Phi_{\text{f}} \rangle \textbf{E}_0 \cdot{\rangle} \Phi_{\text{f}} | \mu (t) | \Phi_{\text{i}} \rangle \]
\[ =\sum\limits_{\text{i,f}} \rho_{\text{i}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu | \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu (t) | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \]
\[ =\sum\limits_{\text{i,f}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} \chi_{\text{iv}} | \mu (\textbf{R}) | \phi_{\text{fr}} \chi_{\text{iv}} \rangle \cdot{\langle} \phi_{\text{fr}} \chi_{\text{iv}} | \mu (\textbf{R},t) | \phi_{\text{ir}} \chi_{\text{iv}} \rangle \]
\[ =\sum\limits_{\text{i,f}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} | \mu_{\text{ave.iv}} | \phi_{\text{fr}} | \mu_{\text{ave.iv}}\text{(t)} | \phi_{\text{ir}} \rangle \]
\[ =\sum\limits_{\text{i}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} | \mu_{\text{ave.iv}} \textbf{E}_0 \cdot{\mu}_{\text{ave.iv}}\text{(t)} | \phi_{\text{ir}} \rangle . \]
При переході від другої до третьої рядки цієї деривації використовувалася наступна ідентичність:
\[ \langle \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu \text{(t)} | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} | e^{\left(\dfrac{\text{iHt}}{\hbar}\right)} \mu e^{\left(-\dfrac{\text{iHt}}{\hbar}\right)} | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \]
\[ =\langle \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} | e^{\left(\dfrac{\text{itH}_{v,r}}{\hbar}\right)} \mu (\textbf{R}) e^{\left(-\dfrac{\text{itH}_{v,r}}{\hbar}\right)} | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle , \]
де H - повний (електронний плюс коливальний плюс обертальний) гамільтоніан і\(\text{H}_{\text{v,r}}\) є коливальним і обертальним гамільтоном для руху по електронній поверхні стану, дипольний момент\(\psi_{\text{ie}}\) якого дорівнює\(\mu (\textbf{R})\). З третього рядка на четверту (приблизний) поділ обертальних і коливальних рухів в\(\text{H}_{\text{v,r}}\)
\[ \text{H}_{\text{v,r}} = \text{H}_{\text{v}} + \text{H}_{\text{r}} \]
був використаний поряд з тим, що\(\chi_{\text{iv}} \text{ is an eigenfunction of } \text{H}_{\text{v}}\):
\[ H_v \chi_{iv} = E_{iv} \chi_{iv} \]
написати
\[ \langle \chi_{iv} | \mu (\textbf{R},t) | \chi_{iv} \rangle = e^{\left(\dfrac{\text{itH}_r}{\hbar}\right)} \langle \chi_{iv} | e^{\left(\dfrac{\text{itH}_v}{\hbar}\right)} \mu (\textbf{R}) e^{\left(-\dfrac{\text{itH}_v}{\hbar}\right)} | \chi_{iv} \rangle e^{\left(-\dfrac{\text{itH}_r}{\hbar}\right)} \]
\[ = e^{\left( \dfrac{\text{itH}_r}{\hbar} \right)} \langle \chi_{\text{iv}} | e^{\left(\dfrac{\text{itE}_{iv}}{\hbar}\right)} \mu (\textbf{R}) e^{\left(-\dfrac{\text{itE}_{iv}}{\hbar}\right)} | \chi_{iv} \rangle e^{\left(-\dfrac{\text{itH}_{r}}{\hbar}\right)} \]
\[ = e^{\left(\dfrac{\text{itH}_{r}}{\hbar}\right)} \langle \chi_{iv} | \mu (\textbf{R}) | \chi_{iv} \rangle e^{\left(-\dfrac{\text{itH}_{r}}{\hbar}\right)} \]
\[ = \mu_{\text{ave.iv}}\text{(t)}. \]
По суті,\(\mu\) замінюється коливально-усередненим електронним дипольним моментом\(\mu_{\text{ave,iv}}\) для кожного початкового коливального стану, який може бути задіяний, і тимчасова кореляційна функція таким чином стає:
\[ \text{C(t)} = \sum\limits_{\text{i}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | \textbf{E}_0 \cdot{\mu}_{\text{ave, iv}}\text{(t)} | \phi_{\text{ir}} \rangle , \]
де\(\mu_{\text{ave, iv}}\text{(t)}\) - усереднений дипольний момент для коливального стану\(\chi_{\text{iv}}\) в момент t, враховуючи, що він був\(\mu_{\text{ave, iv}}\) в момент t = 0. Часова залежність\(\mu_{\text{ave, iv}}\text{(t)}\) індукується ротаційним гамільтоніаном\(\text{H}_r\), як це чітко показано на кроках, описаних вище:
\[ \mu_{\text{ave, iv}}\text{(t)} = e^{\left( \dfrac{\text{itH}_r}{\hbar} \right)} \langle \chi_{\text{iv}} | \mu (\textbf{R}) | \chi_{text{iv}} \rangle e^{\left(-\dfrac{\text{itH}_r}{\hbar}\right)}. \]
У цьому конкретному випадку рівноважне середнє приймається над початковими обертальними станами, ймовірності яких позначаються\(\rho_{\text{ir}}\), будь-якими початковими коливальними станами, які можуть бути заселені, з ймовірностями\(\rho_{\text{iv}}\), і будь-якими заселеними електронними станами, з ймовірностями\(\rho_{\text{ie}}\).
вібраційно-обертальні переходи
Для вібраційно-обертальних переходів в межах одного електронного стану початкове і кінцеве електронні стани однакові, але розрізняються початкове і кінцеве коливальний і обертальний стани. В результаті сума над кінцевими станами, що містяться у виразі,\( \sum\limits_{i,f} \phi_i \textbf{E}_0 \cdot{\langle}\Phi_i | \mu | \Phi_f \rangle \textbf{E}_0 \cdot{\langle} | \mu | \Phi_i \rangle e^{i(\omega_{f,i})t} \) застосовується лише до підсумовування над кінцевим коливальним і обертальним станами. Паралельно розробка, виконана у випадку чистого обертання, наведеному вище, це можна показати наступним чином:
\[ \sum\limits_{i,f} \rho_i \textbf{E}_0 \cdot{\langle} \Phi_i | \mu | \Phi_f \rangle \textbf{E}_0 \cdot{\langle} | \mu \text{(t) }| \Phi_i \rangle \]
\[ = \sum\limits_{i,f} \rho_i\textbf{E}_0 \cdot{\langle}\phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu | \phi_{\text{fr}} \chi_{\text{fv}} \psi_{\text{ie}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{fv}} \psi_{\text{ie}} | \mu \text{(t) }| \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \]
\[ = \sum\limits_{i,f} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle}\phi_{\text{ir}} \chi_{\text{iv}} | \mu (\textbf{R}) | \phi_{\text{fr}} \chi_{\text{fv}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{fv}} | \mu (\textbf{R},t)| \phi_{\text{ir}} \chi_{\text{iv}} \rangle \]
\[ = \sum\limits_{i,f} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle}\phi_{\text{ir}} \chi_{\text{iv}} | \mu (\textbf{R}_e) + \sum\limits_a (R_a - R_{a, eq}) \dfrac{\partial \mu}{\partial R_a} | \phi_{\text{fr}} \chi_{\text{fv}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{fv}} | e^{\left(\dfrac{\text{itH}_r}{\hbar}\right)}\left( \mu (\textbf{R}_e) + \sum\limits_a(R_a - R_{a, eq}) \dfrac{\partial \mu}{\partial R_a} \right) e^{\left(-\dfrac{\text{itH}_r}{\hbar}\right)} | \phi_{\text{ir}} \chi_{\text{iv}} \rangle e^{\left(i\omega_{fv, iv}t\right)} \]
\[ \sum\limits_{i,f} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | \textbf{E}_0 \cdot{\mu_{\text{i,f}}}(\textbf{R}_e)\textbf{E}_0 \cot{\mu_{\text{i,f}}}(\textbf{R}_e,t) | \phi_{\text{ir}} \rangle | \langle \chi_{\text{iv}} | \chi_{\text{fv}} |^2 e^{i\omega_{\text{fv, iv}}t + i\Delta E_{\text{i,f}}\dfrac{t}{\hbar}}, \]
де
\[ \mu_{\text{i,f}}(\textbf{R}_e,t) = e^{\left( \dfrac{\text{itH}_r}{\hbar} \right)} \mu_{\text{i,f}}(\textbf{R}_e) e^{\left( -\dfrac{\text{itH}_r}{\hbar} \right)} \]
електронний перехідний дипольний матричний елемент, оцінений за рівноважною геометрією поглинаючого стану, що виводить його часову залежність від обертального гамільтоніана,\(\text{H}_r\) як у часових кореляційних функціях, розглянутих раніше.
Таким чином, цей розвиток призводить до наступного визначення C (t) для електронного, вібраційного та обертального випадку:
\[ \text{C(t)} = \sum\limits_{\text{i,f}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | \textbf{E}_0 \cdot{\mu_{\text{if}}}(\textbf{R}_e)\textbf{E}_0 \cdot{\mu_{\text{if}}}(\textbf{R}_e,t) | \phi_{\text{ir}} \rangle | \langle \chi_{\text{iv}} | \chi_{\text{fv}} \rangle |^2 e^{\left( i\omega_{\text{fv, iv}}t + \dfrac{i\Delta E_{\text{i,f}}t}{\hbar} \right)} \]
але чиста швидкість поглинання фотонів залишається:
\[ \text{R}_{\text{eq.ave.net}} = \left(\dfrac{1}{\hbar^2}\right)\left( 1 - e^{\left( -\dfrac{\hbar \omega}{kT} \right)} \right) \int\limits g(\omega ) I (\omega )\text{ d}\omega . \]
Тут I (\(\omega \)) - це перетворення Фур'є вищевказаного C (t) і\(\Delta E_{\text{i,f}}\) є адіабатичною різницею електронної енергії (тобто різниця енергій між рівнем v = 0 в кінцевому електронному стані і рівнем v = 0 в початковому електронному стані) для електронного переходу, що представляє інтерес. Вищезгаданий C (t) чітко містить фактори Франка-Кондона, а також залежність від часу
\[ e^{\left( it\omega_{\text{fv, iv}} + i\Delta E_{\text{i,f}}\dfrac{t}{\hbar} \right)} \]
що виробляє спайки\( \delta \) -функції на кожній частоті електронно-коливального переходу та залежності часу обертання, що міститься у величині функції кореляції часу
\[ \langle \phi_{\text{ir}} \textbf{E}_0 \cdot{\mu_{\text{i,f}}} (\textbf{R}_e)\textbf{E}_0\cdot{\mu_{\text{i,f}}}(\textbf{R}_e,t) |\phi_{\text{ir}} \rangle . \]
Підводячи підсумок, функція форми лінії I (\(\omega \)) виробляє чисту швидкість поглинання фотонів
\[ R_{\text{eq.ave.net}} = \left( \dfrac{1}{\hbar^2} \right)\left( 1 - e^{\left(-\dfrac{\hbar \omega}{kT}\right)}\right) \int\limits g(\omega ) I(\omega )\text{ d}\omega \]
у всіх перерахованих вище випадках і I (\( \omega \)) є перетворенням Фур'є відповідної залежної від часу функції C (t) у всіх випадках. Однак чисті випадки обертання, вібрації-обертання та електронно-вібраційного обертання відрізняються формою відповідних C (t).
\[ \text{C(t)} = \sum\limits_i \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | (\textbf{E}_0 \cdot{\mu}_{\text{ave, iv}} ) \textbf{E}_0 \cdot{\mu}_{\text{ave, iv}}(t) | \phi_{\text{ir}} \rangle \]
в чистому обертальному випадку,
\[ \text{C(t)} = \sum\limits_i \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | (\textbf{E}_0 \cdot{\mu}_{\text{trans}} ) \textbf{E}_0 \cdot{\mu}_{\text{trans}}(t) | \phi_{\text{ir}} \rangle e^{it\omega_{\text{fv, iv}}} \]
в електронно-вібро-обертанні випадку.
Усі ці часові кореляційні функції містять часові залежності, що виникають внаслідок обертального руху вектора, пов'язаного з диполем (тобто коливально-усереднений диполь\(\mu_{\text{ave, iv}}(t)\), коливальний перехідний диполь або електронний перехідний диполь\(\mu_{\text{i,f}}(\textbf{R}_{\text{e,t}})\))\(\mu_{\text{trans}}(t)\), а останні два також містять коливальні часові залежності (тобто,\( e^{\left( it\omega_{fv,iv} \right)}\) або\(e^{\left( it\omega_{fv,iv} + i\Delta E_{\text{i,f}}\frac{t}{\hbar} \right)} \)), що виникають внаслідок коливальних або електронно-коливальних різниць рівня енергії. При обробці наступних розділів враховуються обертальні внески за обставин, які характеризують, наприклад, розбавлені газоподібні зразки, де частота зіткнення низька, і рідкофазні зразки, де обертальний рух краще описується з точки зору дифузійного руху.
Механізми розширення ліній
Якщо обертальний рух молекул вважається абсолютно безперешкодним (наприклад, будь-яким середовищем або зіткненнями з іншими молекулами), доцільно висловити часову залежність кожної з дипольних часових кореляційних функцій, перерахованих вище, з точки зору моделі «вільного обертання». Наприклад, при роботі з двоатомними молекулами електроннийколивально-обертальний C (t), відповідний конкретному електронно-коливальному переходу, стає:
\[ \text{C(t)} = \left( \dfrac{1}{\text{q}_r\text{q}_v\text{q}_e\text{q}_t}\right) \sum\limits_J (2J+1) e^{\left( -\dfrac{-h^2J(J+1)}{8\pi^2IkT} \right)}e^{\left( -\dfrac{hv_{\text{vib}}vi}{kT} \right)}g_{ie} \langle \phi_J | \text{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{ie}}(\textbf{R}_e,t) | \phi_J \rangle | \langle \chi_{\text{iv}} | \chi_{\text{fv}} \rangle |^2 e^{\left( ithv_{\text{vib}} + i\Delta E_{\text{i,f}}\dfrac{t}{\hbar} \right)}. \]
Ось,
\[ \text{q}_r = \left( \dfrac{8\pi^2 IkT}{h^2} \right) \]
функція обертального розділення (I - момент\(I = \mu R_e^2, \text{ and } \dfrac{h^2J(J+1)}{8\pi^2I}\) інерції молекули, енергія обертання молекули для стану з квантовим числом J і виродженням 2J+1)
\[ \text{q}_v = \dfrac{ e^{\left( -\dfrac{hv_{\text{vib}}}{2\text{kT}} \right)} }{1 - e^{\left( -\dfrac{hv_{\text{vib}}}{\text{kT}}\right) } } \]
- функція вібраційного розділу (\(v_{\text{vib}}\)будучи коливальною частотою),\(\text{g}_{\text{ie}}\) є виродженням початкового електронного стану,
\[ \text{q}_t = \sqrt[3]{\left( \dfrac{2\pi \text{mkT}}{h^2} \right)}V \]
- функція вібраційного розділу (\(v_{\text{vib}}\)будучи коливальною частотою),\(\text{g}_{\text{ie}}\) є виродженням початкового електронного стану,
\[ \text{q}_t = \sqrt[3]{\dfrac{2\pi mkT}{h^2}}\text{V} \]
функція поступального розділу для молекул маси m, що рухаються в об'ємі V, і\(\Delta E_{\text{i,f}}\) є адіабатичним інтервалом електронної енергії.
Функції\( \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) | \phi_J \rangle \) описують часову еволюцію дипольно-зв'язаного вектора (електронного перехідного диполя в даному випадку) для обертального стану J. У моделі «вільного обертання» ця функція приймається у вигляді:
\[ \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) \phi_J \rangle = \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) \phi_J \rangle \text{Cos}\left( \dfrac{\text{hJ(J + 1)}}{4\pi\text{I}} \right) \]
де
\[ \omega_J = \left( \dfrac{\text{hJ(J + 1)}}{4\pi\text{I}} \right) \]
частота обертання (в циклах в секунду) для обертання молекули в стані, позначеному J. Цю коливальну залежність часу, поєднану з залежністю\( e^{\left( it\omega_{\text{fv,iv}} + i\Delta E_{\text{i,f}} \frac{t}{\hbar} \right)} \) часу, що виникає від електронного і коливального факторів, виробляють, коли ця C (t) функція Фур'є перетворюється на генерацію I ( \(\omega \)) серія\(\delta\) -функція «піки», коли
\[ \omega = \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \]
Інтенсивності цих піків регулюються
\[ \text{C(t)} = \left( \dfrac{1}{\text{q}_r\text{q}_v\text{q}_e\text{q}_t}\right) \sum\limits_J (2J+1) e^{\left( -\dfrac{-h^2J(J+1)}{8\pi^2IkT} \right)}e^{\left( -\dfrac{hv_{\text{vib}}vi}{kT} \right)}g_{ie}. \]
Больцмана населення фактори, а також\( | \langle \chi_{iv}| \chi_{fv} \rangle |^2\) Франка-Кондона фактори і\(\langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) | \phi_J \rangle \) терміни.
Цей же аналіз може бути застосований до чистих залежностей часу обертання та вібрації обертання C (t) з аналогічними результатами. У першому передбачається, що піки\(\delta \) -функцій відбуватимуться при
\[ \omega \pm \omega_J \]
а в останньому при
\[ \omega = \omega_{\text{fv,iv}} \pm \omega_J ; \]
з інтенсивностями, що регулюються незалежними від часу факторами у відповідних виразах для C (t).
При експериментальних вимірах таких різких\(\delta\) -функціональних піків, звичайно, не спостерігається. Навіть коли використовуються лазерні джерела світла з дуже вузькою шириною смуги (тобто, для яких g (\(\omega \)) є надзвичайно вузькопічною функцією), спектральні лінії мають кінцеву ширину. Давайте тепер обговоримо кілька джерел розширення ліній, деякі з яких будуть стосуватися відхилень від представленої вище моделі «безперешкодного» обертального руху.
Допплерівське розширення
У вищезазначених виразах\(C(t)\) for явно показано усереднення над початковим обертальним, коливальним та електронним станами. Існує також середнє значення над поступальним рухом, неявним у всіх цих виразах. Його роль (поки) не підкреслювалася, оскільки рівні молекулярної енергії, відстані яких дають характерні частоти, при яких світло може поглинатися або випромінюватися, не залежать від поступального руху. Однак частота електромагнітного поля, яке відчувають рухомі молекули, залежить від швидкостей молекул, тому зараз це питання потрібно вирішити.
Елементарні класи фізики виражають так званий доплерівський зсув частоти хвилі, індукований рухом або джерела світла, або молекули (Ейнштейн говорить нам, що ці дві точки зору повинні дати однакові результати) наступним чином:
\[ \omega_{\text{observed}} = \omega_{\text{nominal}} \left(\dfrac{1}{1+\dfrac{v_z}{c}}\right) \approx \left( 1 - \dfrac{v_z}{c} + ...\right) . \]
Тут частота нерухомого джерела світла,\(\omega_{\text{nominal}}\) яку бачать нерухомі молекули,\(v_z\) - це швидкість відносного руху джерела світла та молекул, c - швидкість світла, а\(\omega_{\text{observed}}\) також частота зсуву доплера (тобто частота, яку бачать молекули). Друга ідентичність отримується шляхом розширення в ряді потужності\(\left(1 + \dfrac{v_z}{c}\right)^{-1}\) коефіцієнта, і дійсна в усіченому вигляді, коли молекули рухаються зі швидкістю, значно нижчою від швидкості світла.
Для всіх розглянутих раніше випадків функція C (t) піддається перетворенню Фур'є для отримання спектральної лінійної функції I (\(\omega\)), яка потім забезпечує істотний інгредієнт для обчислення чистої швидкості поглинання фотонів. У цьому процесі перетворення\(\omega\) Фур'є змінна вважається частотою електромагнітного поля, яке відчувають молекули. Наведені вище міркування доплерівського зсуву призводять до розуміння того, що правильна функціональна форма для використання при перетворенні C (t) в I (\(\omega\)) є:
\[ I(\omega ) = \int C(t) e^{-t\omega \left( 1 - \dfrac{v_z}{c} \right)} \text{dt} ,\]
де\(\omega \) - номінальна частота джерела світла.
Як говорилося раніше, в межах С (t) також існує середнє рівновага над поступальним рухом молекул. Для газофазного зразка, що зазнає випадкових зіткнень і при тепловій рівновазі, це середнє значення характеризується добре відомим розподілом швидкостей Максвелла-Больцмана:
\[ \sqrt{\left( \dfrac{m}{2\pi kT} \right)^3} e^{\left( \dfrac{-m\left( v_x^2 + v_y^2 + v_z^2 \right)}{2kT}\right)}dv_x dv_y dv_z .\]
Тут m - маса молекул і\(v_x, v_y, \text{ and }v_z\) мітка швидкостей вздовж лабораторії фіксованих декартових координат.
Визначаючи вісь z як напрямок поширення фотонів світла і здійснюючи усереднення коефіцієнта Доплера над таким розподілом швидкостей, отримують:
\[ \int\limits_{-\infty}^{\infty} e^{-it\omega \left( 1- \dfrac{v_z}{c} \right)} \sqrt{\left( \dfrac{m}{2\pi kT} \right)^3} e^{\left( \dfrac{-m(v_x^2 + v_y^2 + v_z^2)}{2kT} \right)}dv_x dv_y dv_z \]
\[ = e^{-\omega t} \int\limits_{-\infty}^{\infty}\sqrt{\dfrac{m}{2\pi kT}}e^{\left(\dfrac{i\omega tv_z}{c}\right)} e^{\left( \dfrac{-mv_z}{2kT} \right)} dv_z \]
\[ =e^{-\omega t} e^{\left( \dfrac{-\omega^2t^2kT}{2mc^2} \right)} \]
Цей результат при підстановці у вирази для C (t) дає вирази, ідентичні тим, що наведено для трьох випадків, розглянутих вище, але з однією модифікацією. Середнє значення поступального руху більше не потрібно розглядати в кожному C (t); натомість попередні вирази для C (t) повинні бути помножені на коефіцієнт,\( e^{\frac{-\omega^2 t^2kT}{2mc^2}} \) який втілює поступально усереднений доплерівський зсув. Функцію форми спектральної лінії I (\(\omega\)) потім можна отримати для кожного C (t) простим перетворенням Фур'є:
\[ I(\omega) = \int\limits_{-\infty}^{\infty} e^{-i\omega t}C(t)\text{dt}. \]
При застосуванні до випадків обертання, вібрації-обертання або електронно-вібрації-обертання в рамках «безперешкодної» моделі обертання, обробленої раніше, перетворення Фур'є включає інтеграли виду:
\[ I(\omega) = \int\limits_{-\infty}^{\infty} e^{-\omega t}e^{\dfrac{-\omega^2 t^2kT}{2mc^2}}e^{it \left(\omega_{\text{fv,iv}} + \Delta \dfrac{E_{\text{i,f}}}{\hbar} \pm \omega_J \right)} \text{dt}.\]
Цей інтеграл виникне у випадку електронно-вібрації-обертання; інші два випадки включали б інтеграли тієї ж форми, але з\( \frac{\Delta E_{\text{i,f}}}{\hbar} \) відсутніми в ситуації вібрації-обертання та\(\omega_{\text{fv, iv}} + \frac{\Delta E_{\text{i,f}}}{\hbar}\) відсутніми для чистих переходів обертання. Всі такі інтеграли можуть бути проведені аналітично і дають:
\[ I(\omega ) = \sqrt{\dfrac{2mc^2\pi}{\omega^2 kT}}e^{\left( \dfrac{-\left(\omega - \omega_{\text{fv, iv}} - \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J\right)^2 mc^2}{2\omega^2 kT} \right)}. \]
Результатом є ряд гаусових «піків» в\(\omega\) -просторі, зосереджених на:
\[ \omega = \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \]
з шириною (\(\sigma)\)визначається
\[ \sigma^2 = \dfrac{\omega^2kT}{mc^2}, \]
з огляду на температуру\(T\) і масу молекул\(m\). Чим гарячіше зразок, тим швидше рухаються молекули в середньому, і тим ширше розподіл зміщених доплерівських частот, які відчувають ці молекули. Тоді чистий результат ефекту Доплера полягає у створенні функції форми лінії, подібної до серії -функцій моделі «безперешкодного» обертання, але з кожним піком\(\delta\)\(\delta\) -функції розширюється до гаусової форми.
Розширення тиску
Щоб включити вплив зіткнень на частину обертального руху будь-якої з перерахованих вище C (t) функцій, потрібно ввести модель того, як такі зіткнення змінюють дипольно-пов'язані вектори, що входять в C (t). Найбільш елементарна модель, яка використовується для вирішення зіткнень, застосовується до газоподібних зразків, які, як передбачається, зазнають безперешкодного обертального руху, поки не вдарить інша молекула, в цей час до дипольного вектора наноситься рандомізуючий «удар» і після чого молекула повертається до свого безперешкодного обертального руху.
Ефекти таких колізійно індукованих ударів розглядаються в рамках так званої моделі розширення тиску (іноді її називають колізійним розширенням) шляхом модифікації кореляційної функції вільного обертання шляхом введення експоненціального коефіцієнта демпфування \(e^{\frac{-|t|}{\tau}}\):\(\tau\) Вважається, що параметр часової шкали
\[ \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) | \phi_J\rangle Cos \left( \dfrac{hJ(J+1)t}{4\pi I} \right) \]
\[ \rightarrow \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) | \phi_J\rangle Cos\left( \dfrac{hJ(J+1)t}{4\pi I} \right) e^{\dfrac{-|t|}{\tau}}. \]
цієї демпфуючої функції характеризує середній час між зіткненнями і, таким чином, повинен бути обернено пропорційним зіткненню частоти. Його величина також пов'язана з ефективністю, з якою зіткнення змушують дипольну функцію відхилятися від її безперешкодного обертального руху (тобто пов'язаного з силою зіткнення). По суті, експоненціальне демпфування призводить\( \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t)|\phi_J\rangle \) до того, що функція часової кореляції «втрачає свою пам'ять» і затухає до нуля; ця точка зору «пам'яті» заснована на перегляді\( \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) | \phi_J\rangle \) як проекції\( \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) \) вздовж її значення t=0\( \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) \) як функції часу t.
Введення цієї додаткової залежності\( e^{\frac{-|t|}{\tau}} \) часу в C (t) дає, коли C (t) перетворюється Фур'є для генерації I (\(\omega\)),
\[ I(\omega ) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{\dfrac{-|t|}{\tau}}e^{\dfrac{-\omega^2 t^2kT}{2mc^2}}e^{it\left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)}\text{dt} . \]
У межі дуже малого доплерівського розширення\( \frac{\omega^2t^2kT}{2mc^2} \) коефіцієнт можна ігнорувати (тобто\( e^{\frac{-\omega^2t^2kT}{2mc^2}} \) встановити рівний одиниці), і
\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-\left(\dfrac{|t|}{\tau}\right)}e^{\left( it\left( \omega_{\text{fv,iv}}+\dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)\right)} \text{dt} \]
результати. Цей інтеграл може бути виконаний аналітично і генерує:
\[ I(\omega) = \dfrac{1}{4\pi}\left( \dfrac{\dfrac{1}{\tau}}{\left( \dfrac{1}{\tau} \right)^2 + \left( \omega - \omega_{\text{fv,iv}} -\dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J\right)^2} + \dfrac{\dfrac{1}{\tau}}{\left( \dfrac{1}{\tau} \right)^2 + \left( \omega + \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} \right) \]
пару вершин Лоренціана в\(\omega\) -просторі знову по центру
\[ \omega = \pm \left[ \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right]. \]
повної ширини на половині висоти ці Лоренціанські вершини є\(\frac{2}{\tau}\). Один каже, що окремі піки були тиску або зіткнення розширені.
Коли доплерівським розширенням не можна нехтувати щодо колізійного розширення,
\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-\omega t}e^{-\dfrac{|t|}{\tau}}e^{-\dfrac{\omega^2t^2kT}{2mc^2}}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt}\]
вищевказаний інтеграл виконати складніше. Тим не менш, це може бути здійснено і знову виробляє ряд піків, зосереджених на,
\[ \omega = \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \]
але ширина яких визначається як Допплером, так і ефектами розширення тиску. Таким чином, результуючі форми ліній вже не є чисто Лоренціанськими або гауссовими (які порівнюються на малюнку нижче для обох функцій, що мають однакову повну ширину на половині висоти та однакову інтегровану область), але мають форму, яка називається формою Войта.
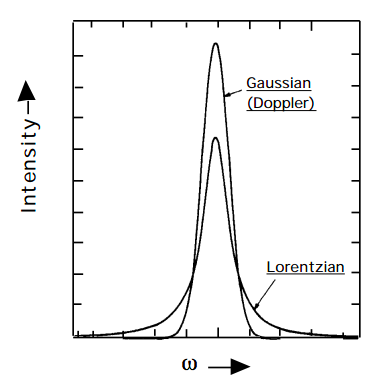
Малюнок 15.4.1: Вставте сюди підпис!
Ротаційне розширення дифузії
Молекули в рідинях і дуже щільних газах зазнають частих зіткнень з іншими молекулами; тобто середній час між зіткненнями короткий порівняно з періодом обертання для їх безперешкодного обертання. В результаті залежність від часу дипольної кореляційної функції більше не може бути змодельована з точки зору вільного обертання, яке переривається (нечастими) зіткненнями і зміщенням Доплера. Натомість модель, яка описує безперервне буферування диполя молекули навколишніми молекулами, стає доречною. Для рідких зразків, в яких ці часті зіткнення змушують диполь молекули зазнавати кутових рухів, які охоплюють всі кути (тобто, на відміну від замороженого скла або твердого тіла, в якому диполь молекули зазнає сильно збуреного маятникового руху про деяку сприятливу орієнтацію), так званий Часто використовується модель ротаційної дифузії. На цій картині залежна від обертання частина C (t) виражається так:
\[ \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t)|\phi_J\rangle = \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) |\phi_J\rangle e^{-2D_{\text{rot}}|t|}, \]
де D\(_{\text{rot}}\) - константа обертальної дифузії, величина якої деталізує спад часу в\( \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t)\) усередненому значенні часу t щодо до його значення в момент t = 0; чим більше D\(_{\text{rot}}\), тим швидше відбувається цей розпад.
Як і при розширенні тиску, ця експоненціальна залежність часу, піддаючись перетворенню Фур'є, дає:
\[ I(\omega) = \int\limits^{\infty}_{-\infty}e^{-i\omega t}e^{-2D_{\text{rot}}|t|}e^{\dfrac{-\omega^2t^2kT}{2mc^2}}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)}\text{dt}. \]
Знову ж таки, в межі дуже малого доплерівського розширення\( \frac{\omega^2t^2kT}{2mc^2} \) коефіцієнт може бути ігнорується (тобто\( e^{-\frac{\omega^2t^2kT}{2mc^2}} \)) встановити дорівнює одиниці), і
\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-2D_{\text{rot}}|t|}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt} \]
результати. Цей інтеграл може бути оцінений аналітично і генерує:
\[ I(\omega) = \dfrac{1}{4\pi}\left( \dfrac{2D_{\text{rot}}}{(2D_{\text{rot}})^2 + \left( \omega -\omega_{\text{fv,iv}} - \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} + \dfrac{2D_{\text{rot}}}{(2D_{\text{rot}})^2 + \left( \omega + \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} \right), \]
пару вершин Лоренціана в\(\omega\) -просторі знову по центру
\[ \omega = \pm \left[ \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right]. \]
повної ширини на половині висоти з цих Лоренціанських вершин 4D\(_{\text{rot}}\). У цьому випадку можна сказати, що окремі піки були розширені за допомогою обертальної дифузії. Коли доплерівським розширенням не можна нехтувати щодо колізійного розширення,
\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-2D_{\text{rot}}|t|}e^{-\dfrac{\omega^2t^2kT}{2mc^2}}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt.} \]
вищевказаний інтеграл виконати складніше. Тим не менш, це може бути здійснено і знову виробляє ряд піків, зосереджених на,
\[ \omega = \pm \left[ \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right] \]
але ширини яких визначаються як доплерівськими, так і обертальними дифузійними ефектами.
Час життя або однорідне розширення Гейзенберга
Всякий раз, коли поглинаючий вид зазнає одного або декількох процесів, які виснажують його чисельність, ми говоримо, що він має кінцевий термін життя. Наприклад, вид, який зазнає одномолекулярної дисоціації, має кінцевий термін життя, як і збуджений стан молекули, яка розпадається спонтанним випромінюванням фотона. Будь-який процес, який виснажує поглинаючі види, сприяє іншому джерелу залежності часу для дипольних часових кореляційних функцій C (t), розглянутих вище. Ця залежність від часу зазвичай моделюється шляхом додавання, мультиплікативним чином, множника\( e^{-\frac{|t|}{\tau}} \). Це, в свою чергу, змінює функцію форми лінії I (\(\omega\)) таким чином, як це обговорювалося при обробці випадку ротаційної дифузії:
\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-\dfrac{|t|}{\tau}}e^{-\dfrac{\omega^2t^2kT}{2mc^2}}e^{\left( it\left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt}. \]
Не дивно, що коли внесок Доплера невеликий, можна отримати:
\[ I(\omega) = \dfrac{1}{4\pi} \left( \dfrac{\dfrac{1}{\tau}}{\left(\dfrac{1}{\tau}\right)^2 \left( \omega - \omega_{\text{fv,iv}} - \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2 } + \dfrac{\dfrac{1}{\tau}}{\left( \dfrac{1}{\tau} \right)^2 + \left( \omega + \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} \right). \]
У цих лініях Лоренціана параметр\(\tau\) описує час життя кінетичного розпаду молекули. Один каже, що спектральні лінії були життя або Гейзенберг розширений на величину, пропорційну\(\frac{1}{\tau}\). Остання термінологія виникає тому, що кінцевий термін життя молекулярних станів може розглядатися як продукування, через відношення невизначеності Гейзенберга\( \Delta E\Delta t > \hbar \), станів, енергія яких є «невизначеною» в межах кількості\(\Delta\) Е.
Неоднорідне розширення ділянки
Серед вищезазначених механізмів розширення лінії тиск, обертальна дифузія та розширення терміну служби - все це однорідне різноманіття. Це означає, що на кожну молекулу в зразку впливає точно так само процес розширення. Наприклад, одні не знаходять одних молекул з коротким терміном життя, а інші з тривалим терміном життя, у випадку Гейзенберга; весь ансамбль молекул характеризується одним життям.
На відміну від цього, доплерівське розширення є неоднорідним за своєю природою, оскільки кожна молекула відчуває розширення, характерне для її особливої природи (швидкість\(v_z\) в даному випадку). Тобто швидкі молекули мають свої лінії розширені більше, ніж у більш повільних молекул. Іншим важливим прикладом неоднорідного розширення є так зване розширення ділянки. Молекули, вбудовані в рідину, тверде тіло або скло, в момент поглинання фотонів не відчувають абсолютно однакових взаємодій зі своїм оточенням. Розподіл миттєвих «сольватаційних» середовищ може бути досить «вузьким» (наприклад, у високо впорядкованої твердої матриці) або досить «широким» (наприклад, у рідині при високій температурі). Різні середовища виробляють різний рівень енергії розщеплення
\[ \omega = \omega_{\text{fv,iv}} + \frac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \]
оскільки початковий і кінцевий стани по-різному «вирішуються» оточенням і, таким чином, різними частотами, при яких може відбуватися поглинання фотонів. Розподіл енергетичного рівня розщеплення змушує зразок поглинати в діапазоні частот, як показано на малюнку нижче, де порівнюються однорідні та неоднорідні форми ліній.
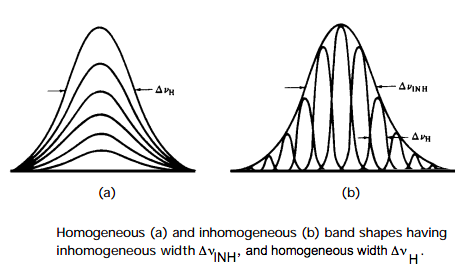
Функція форми спектральної лінії I (\(\omega\)) додатково розширюється, коли неоднорідність ділянки присутня та значна. Ці ефекти можуть бути змодельовані шляхом згортання виду I (\(\omega\)) функції, що виникає в результаті доплера, життя, обертальної дифузії та розширення тиску за допомогою гаусового розподілу P (\(\Delta E\)), що описує неоднорідний розподіл розщеплення енергетичного рівня:
\[ I(\omega) = \int\limits I^0(\omega ;\Delta E) P(\Delta E) d\Delta E. \]
Тут I\(^0(\omega ;\Delta E)\) - функція форми лінії, така як описані раніше, кожна з яких містить набір частот (наприклад,\( \omega = \omega_{\text{fv,iv}} + \frac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J = \omega + \frac{\Delta E}{\hbar})\) при яких відбувається поглинання або випромінювання.
Загальний експериментальний тест на неоднорідне розширення включає випалювання отворів. У таких експериментах інтенсивне джерело світла (часто лазер) налаштовується на частоту\(\omega_{\text{burn}}\), яка лежить в межах досліджуваної спектральної лінії для неоднорідного розширення. Потім використовується другий перебудовується джерело світла для сканування через профіль спектральної лінії, і, наприклад, записується спектр поглинання. З огляду на профіль поглинання, як показано нижче, при відсутності інтенсивного горіння джерела світла:
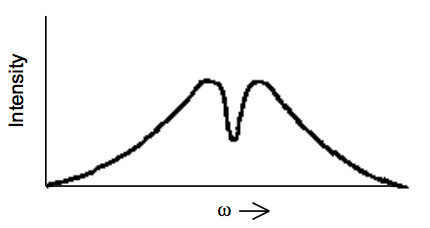
один очікує побачити профіль, такий як показано нижче:

Малюнок 15.4.4: Вставте сюди підпис!
якщо неоднорідне розширення є оперативним.
Розшифровка зміни профілю поглинання, викликаного яскравим джерелом світла, проходить наступним чином:
- В ансамблі молекул, що містяться в зразку, деякі молекули будуть поглинати з частотою яскравого джерела світла або поблизу неї\(\omega_{\text{burn}}\); інші молекули (ті, чиї середовища не виробляють поділу енергетичного рівня, які відповідають\(\omega_{\text{burn}}\)) не поглинають на цій частоті.
- Ті молекули, які поглинають за бажанням\(\omega_{\text{burn}}\), мають свій перехід насичений інтенсивним джерелом світла, тим самим роблячи цю частотну область профілю лінії прозорою для подальшого поглинання.
- Коли «зонд» джерело світла сканується над лінійним профілем, це спричинить поглинання для тих молекул, локальне середовище яких не дозволяло їм насичуватися\(\omega_{\text{burn}}\) світлом. Профіль поглинання, записаний детектором цього зонда джерела світла, таким чином, буде відповідати профілю вихідної лінії, поки
- частота зондового джерела світла відповідає\(\omega_{\text{burn}}\), при якій не буде зафіксовано поглинання фотонів джерела зонда, оскільки молекули, які поглинають у цьому частотному режимі, були насичені.
- Отже, «отвір» з'явиться в спектрі, записаному детектором джерела світла зонда в області\(\omega_{\text{burn}}\).
На жаль, техніка випалювання отворів не забезпечує повністю надійного методу виявлення неоднорідно розширених ліній. Якщо в такому пекучому експерименті спостерігається дірка, це дає достатньо доказів, але якщо його не видно, результат не є остаточним. В останньому випадку перехід може бути недостатньо сильним (тобто може не мати досить великої «швидкості поглинання фотонів»), щоб інтенсивне джерело світла наситило перехід в обсязі, необхідному для утворення отвору.
На цьому наше знайомство з темою молекулярної спектроскопії завершено. Більш досконалі методи лікування багатьох предметів, розглянутих тут, а також багато аспектів сучасної експериментальної спектроскопії можна знайти в тексті Zare про кутовий імпульс, а також в тексті Штайнфельда Молекули і випромінювання, 2\(^{nd}\) видання, J.I. Steinfeld, MIT Press (1985).
