15.1: Обертальні переходи

У межах наближення, що електронний, коливальний та обертальний стани молекули можуть розглядатися як незалежні, загальна молекулярна хвильова функція «початкового» стану є продуктом

\[ \Phi_i = \psi_{ei} \chi_{vi} \phi_{ri} \]

електронної функції\(\psi_{ei}, \text{ a vibrational function } \chi_{vi}, \text{ and a rotational function } \phi_{ri}. \text{ A similar product expression holds for the "final" wavefunction } \Phi_f.\)

У мікрохвильовій спектроскопії енергія випромінювання лежить в діапазоні фракцій a\(cm^{-1} \text{ through several } cm^{-1}\); такі енергії адекватні для збудження обертальних рухів молекул, але недостатньо високі, щоб збуджувати будь-які, але найслабші вібрації (наприклад, слабо зв'язаних комплексів Ван дер Ваальса). При обертальних переходах електронний і коливальний стани таким чином залишаються незмінними процесом збудження; отже,\(\psi_{ei} = \psi_{ef} \text{ and } \chi_{vi} = \chi_{vf}.\)

Застосування виразів швидкості переходу електричного диполя першого порядку

\[ R_{i,f} = 2\pi g(\omega_{f,i}) |\alpha_{f,i}|^2 \]

отримана в розділі 14, до цього випадку вимагає, щоб наближення Е1

\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2} \right) g(\omega_{f,i}) | \textbf{E}_0\cdot{\langle}\Phi_f |\mu | \Phi_i \rangle |^2 \]

бути розглянуті більш детально. Зокрема, електричні дипольні матричні елементи\( \langle \Phi_f | \mu | \Phi_i \rangle \text{ with } \mu = \sum\limits_j e \textbf{r}_j + \sum\limits_a Z_a e \textbf{R}_a \) повинні бути проаналізовані на\(\Phi_i \text{ and } \Phi_f\) предмет форми продукту, показаної вище.

Інтеграції над електронними координатами, що містяться в, а\( \langle \Phi_f |\mu |\Phi_i \rangle ,\) також інтеграції над коливальними ступенями свободи дають «очікувані значення» оператора електричного дипольного моменту, оскільки електронна та коливальна компоненти\( \Phi_i \text{ and } \Phi_f\) ідентичні:

\[ \langle \psi_{ei}| \mu | \psi_{ei} \rangle = \mu(\textbf{R}) \]

є дипольним моментом початкового електронного стану (який є функцією внутрішніх геометричних ступенів свободи молекули, що позначається R); і

\[ \langle \chi_{vi} | \mu (\textbf{R} ) |\chi_{vi} \rangle = \mu_{ave} \]

- це коливально-усереднений дипольний момент для конкретного вібраційного стану, позначеного\(\chi_{vi}. \text{ The vector } \mu_{ave}\) mave, має компоненти вздовж різних напрямків і може розглядатися як вектор, «заблокований» до внутрішньої координатної осі молекули (позначені a, b, c, як показано нижче).

Малюнок 15.1.1: Вставте сюди підпис!

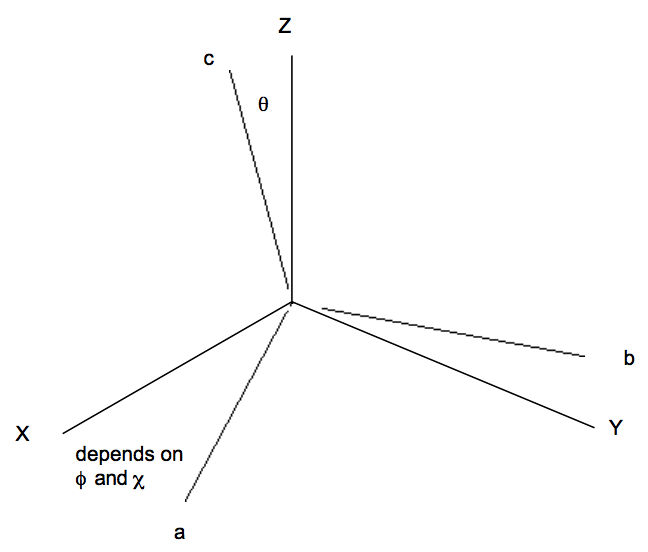
Обертальна частина\( \langle \Phi_f | \mu | \Phi_i \rangle \) інтеграла не має форми очікуваного значення, оскільки початкова обертальна функція\(\phi_{ir} \text{ is not the same as the final } \phi_{fr}\). Цей інтеграл має вигляд:

\[ \langle \Phi_{ir} | \mu_{ave} | \Phi_{fr} \rangle = \int (Y^{\text{*}}_{L,M}(\theta,\phi)) \mu_{ave} Y_{\text{L', M'}}(\theta, \phi) \text{ sin}\theta \text{ d}\theta \text{ d}\phi \]

або лінійні молекули, початкові та кінцеві обертальні\(Y_{\text{L,M}} \text{ and } Y_{\text{L',M'}} \) хвильові функції яких відповідно і

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle = \sqrt{\dfrac{2L + 1}{8\pi^2}}\sqrt{\dfrac{2L' + 1}{8\pi^2}} \]

\[ \int \left( D_{\text{L, M, K}}(\theta , \phi , \chi) \mu_{ave} D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi) \text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \right) \]

для сферичних або симетричних верхніх молекул (тут наведені\( \sqrt{\dfrac{2L + 1}{8\pi^2}}D^{\text{*}}_{\text{L, M, K}}(\theta , \phi , \chi) \) нормовані обертальні хвильові функції, описані в главі 13 і в Додатку G). Кути\(\theta , \phi , \text{ and } \chi\) відносяться до того, як система координат, фіксована молекулою, орієнтована відносно фіксованої простором системи осі X, Y, Z.

Лінійні молекули

Для лінійних молекул коливально-усереднений дипольний момент\(\mu_{ave}\) лежить вздовж молекулярної осі; отже, його орієнтація в лабораторно-фіксованій системі координат може бути визначена через ті ж кути,\((\theta \text{ and } \phi)\) які використовуються для опису обертальних функцій.\(Y_{\text{L,M}} (\theta ,\phi ).\) Отже, три компоненти \( \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle\)інтеграла можна записати як:

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_x = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_y = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_z = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]

де\(\mu\) - величина усередненого дипольного моменту. Якщо молекула не має дипольного моменту, всі перераховані вище електричні дипольні інтеграли зникають, а інтенсивність обертальних переходів Е1 дорівнює нулю.

Три інтеграли E1 можна додатково проаналізувати, зазначивши, що cos\( \theta \propto \text{ Y}_{\text{1,0}}; \text{ sin}\theta \text{ cos}\phi \propto \text{ Y}_{\text{1,1}} + \text{ Y}_{\text{1,-1}}; \text{ and sin}\theta \text{ sin}\phi \propto \text{ Y}_{\text{1,1}} - \text{ Y}_{\text{1,-1}}\) та використовуючи методи зв'язку з кутовим імпульсом, проілюстровані в додатку G. Зокрема, результат, наведений у цьому додатку:

\[ D_{\text{j, m, m'}}D_{\text{l, n, n'}} = \sum\limits_{\text{J, M, M'}}\langle J,M|j,m; l,n\rangle \langle j,m'; l,n'|J,M' \rangle D_{\text{J, M, M'}} \]

при множенні на D\(^{\text{*}}_{\text{J, M, M'}} \text{ and integrated over sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi\) дає:

\[ \int D^{\text{*}}_{\text{J, M, M'}} D_{\text{j, m, m'}}D_{\text{l, n, n'}} \text{ sin}\theta\text{ d}\theta \text{ d}\phi \text{ d}\chi \]

\[ = \dfrac{8\pi^2}{2J+1}\langle \text{ J,M| j,m ; l,n }\rangle \langle \text{ j,m' ; l,n'|J, M' } \rangle \]

\[ = 8\pi^2 \left( \dfrac{jlJ}{mn-M} \right) \left( \dfrac{jlJ}{m'n'-M'} \right) \left( -1 \right)^{\text{M+M'}}. \]

Щоб використати цей результат у поточному випадку лінійно-молекули, відзначимо, що\(D_{\text{J,M,K}} \text{ functions and the Y}_{\text{J,M}}\) функції пов'язані між собою:

\[ \text{Y}_{\text{J,M}}(\theta ,\phi ) = \sqrt{\dfrac{2J + 1}{4\pi}} D^{\text{*}}_{\text{J, M, 0}}(\theta ,\phi ,\chi). \]

Фактор нормалізації тепер\( \sqrt{\frac{2J + 1}{4\pi}} \text{ rather than} \sqrt{\frac{2J + 1}{8\pi^2}}\) тому, що\(\text{Y}_{\text{J,M}}\) вони більше не є функціями\(\chi\), і, таким чином, необхідність інтеграції\( 0 \leq \chi \leq 1\pi\) зникає. Аналогічним чином\(\chi \text{-dependence of}\)\(\text{D}^{\text{*}}_{\text{J,M,K}}\) зникає для K = 0.

Тепер ми використовуємо ці тотожності в трьох інтегралах E1 форми

\[ \mu \int Y^{\text{*}}_{\text{L,M}}(\theta ,\phi) Y_{\text{1,m}}(\theta , \phi) Y_{\text{L',M'}}(\theta ,\phi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi , \]

при цьому m = 0 є інтегралом по осі Z, а інтеграли осі Y та X- є комбінаціями результатів m = 1 та m = -1. Роблячи це дає:

\[ \mu \int Y^{\text{*}}_{\text{L,M}}(\theta , \phi) Y_{\text{1,m}}(\theta ,\phi )\text{ Y}_{\text{L', M'}}(\theta ,\phi) \text{ sin}\theta \theta{ d}\theta \text{ d}\phi \]

\[ =\mu \sqrt{\dfrac{2L + 1}{4\pi} \dfrac{2L' + 1}{4\pi} \dfrac{3}{4\pi}}\int D_{\text{L, M, 0}}\textbf{ D}^{\text{*}}_{\text{l, m, 0}}\textbf{D}^{\text{*}}_{\text{L', M', 0}} \text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\dfrac{\chi}{2\pi}. \]

Останній множник\(1/2\pi\) вставляється для скасування інтеграції над\(d\chi \) цим, оскільки всі K-фактори в матрицях обертання дорівнюють нулю, тривіально виходять\(2\pi \). Тепер, використовуючи результат, показаний вище, виражаючи інтеграл над трьома матрицями обертання, ці інтеграли E1 для випадку лінійної молекули зводяться до:

\[ \mu \int\text{ Y}^{\text{*}}_{\text{L,M}}(\theta , \phi)\text{ Y}_{\text{1,m}}(\theta ,\phi)\text{ Y}_{\text{L',M'}}(\theta ,\phi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]

\[ = \mu \sqrt{\dfrac{2L + 1}{4\pi}\dfrac{2L' + 1}{4\pi}\dfrac{3}{4\pi}}\dfrac{8\pi^2}{2\pi}\left( \dfrac{L' 1 L}{M'm-M} \right)\left( \dfrac{L' 1 L}{0 0 -0} \right)(-1)^M \]

\[ \mu\sqrt{(2L + 1)(2L' + 1)\dfrac{3}{4\pi}}\left( \dfrac{L' 1 L}{M' m -M} \right) \left( \dfrac{L' 1 L}{0 0 -0} \right) (-1)^M. \]

Застосовується до інтеграла по осі z (ідентифікуючи m = 0), цей результат зникає, якщо:

\[ \text{M} = \text{M'} \]

і

\[ \text{L} = \text{L'} + 1 \text{ or L' }- 1. \]

Незважаючи на те, що міркування про зв'язок кутового моменту дозволять L = L '(оскільки з'єднання двох кутових моментів з j = 1 і j = L' повинно дати L'+1, L' та L'-1), символ 3-j\( \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) \) зникає для випадку L = L ', оскільки символи 3-j мають наступну симетрію

\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) = (-1)^{\text{L+L'+1}} \left( \dfrac{\text{L' 1 L}}{\text{-M' -m M}} \right) \]

щодо індексів M, M' та m. Застосовується до символу\( \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) \) 3-j, це означає, що цей конкретний 3-j елемент зникає для L = L ', оскільки L + L' + 1 непарний і, отже\((-1)^{\text{L + L' + 1}}\), -1.

Застосовується до інтегралів по осі x та y, які містять m = ± 1 компоненти, цей самий аналіз дає:

\[ \mu \sqrt{\text{(2L + 1)(2L' + 1)}\dfrac{3}{4\pi}}\left( \dfrac{\text{L' 1 L}}{M' \pm 1 -M} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) (-1)^M \]

який потім вимагає, щоб

\[ \text{M} = \text{M'} \pm 1 \]

і

\[ \text{L} = \text{ L' + 1, L' -1} \]

з L = L' знову забороняється через другий символ 3-j.

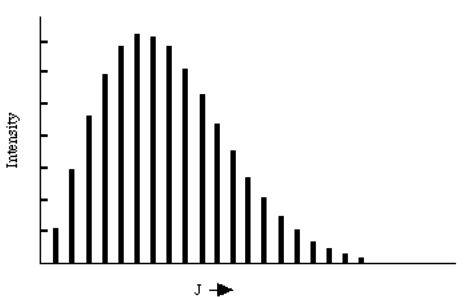
Ці результати дають так звані "правила вибору", оскільки граничні значення L і M кінцевого обертального стану, враховуючи L', M' значення початкового обертального стану. На малюнку, показаному нижче, наведено спектр поглинання L = L' + 1 при 120° К. Інтенсивності різних піків пов'язані з популяціями нижчих енергетичних обертальних станів, які, в свою чергу, пропорційні\((2 L' + 1) e^{(- L'(L'+1) \dfrac{\hbar^2}{8\pi^2IkT}}.\) Також в інтенсивності включені так звані коефіцієнти сили лінії, пропорційні квадратам величин:

\[ \mu \sqrt{ (2L + 1)(2L' + 1)\dfrac{3}{4\pi} }\left( \dfrac{\text{L' 1 L}}{M' m -M} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right)(-1)^M \]

які з'являються в аналізованих вище інтегралах Е1 (нагадаємо, що швидкість поглинання фотонів\( R_{i,f} = \left( \frac{2\pi}{\hbar^2} \right)g(\omega_{f,i}) | \textbf{E}_0\cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \) включає квадрати цих матричних елементів). Книга Zare дає відмінну обробку факторів сили лінії внесок у обертання, вібрацію та інтенсивність електронної лінії.

Малюнок 15.1.2: Вставте сюди підпис!

Нелінійні молекули

Для молекул, які є нелінійними і обертальні хвильові функції яких задаються через сферичні або симетричні верхні функції\(\textbf{D}^{\text{*}}_{\text{L,M,K}}\), дипольний момент\(\mu_{ave}\) може мати компоненти вздовж будь-якої або всіх трьох внутрішніх координат молекули (наприклад, три фіксовані молекули координати, які описують орієнтація головних осей моменту інерції (тензора). Для сферичної верхньої молекули\(| \mu_{ave} |\) зникає, тому переходи Е1 не відбуваються.

Для симетричних верхніх видів,\(\mu_{ave}\) лежить вздовж осі симетрії молекули, тому орієнтація\(\mu_{ave}\) може бути знову описана в терміні\(\theta \text{ and } \phi \), кути, використовувані для розташування орієнтації осі симетрії молекули щодо фіксованої лабораторії системи координат. В результаті інтеграл Е1 знову можна розкласти на три частини:

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_x = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi)\text{ cos}\theta \text{ cos}\phi D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \]

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_y = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi)\text{ cos}\theta \text{ sin}\phi D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \]

\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_z = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi) \text{ cos}\theta D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \]

Використання того, що\( \text{ cos}\theta \propto \text{D}^{\text{*}}_{\text{1, 0,0}}; \text{ sin}\theta \text{ cos}\phi \propto \text{D}^{\text{*}}_{\text{1,1,0}} + \text{D}^{\text{*}}_{\text{1,-1,0}}; \text{ and sin}\theta \text{ sin}\phi \propto \text{D}^{\text{*}}_{\text{1,1,0}} - \text{D}^{\text{*}}_{\text{1,-1,0}}\) і інструменти зчеплення моменту моменту дозволяє виражати ці інтеграли, як зазначено вище, в терміні добутку наступних 3-j символів:

\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) \left( \dfrac{\text{L' 1 L}}{\text{K' 0 -K}} \right), \]

з якого виводяться такі правила вибору:

\[ \text{L} = \text{L' + 1, L', L' - 1} \text{ (but not L = L' = 0)} \]

\[ \text{K = K'} \]

\[ \text{M = M' + m,} \]

з m = 0 для інтеграла по осі Z і m = ± 1 для інтегралів осі X- і Y. Крім того, якщо K = K '= 0, переходи L = L' також заборонені зникненням другого символу 3-j.

Дописувачі та атрибуція

• Template:ContribSimonsNichols