7.2: Класична взаємодія світла та матерії

Класичні плоскі електромагнітні хвилі

В якості відправної точки корисно спочатку узагальнити класичний опис електромагнітних полів. Виведення плоских хвильових розв'язків електричного та магнітного полів та векторного потенціалу описано в додатку розділу 6.6.

Рівняння Максвелла описують електричні (\(\overline {E}\)\(\overline {B}\)) та магнітні поля (); однак для побудови гамільтоніана ми повинні використовувати залежний від часу потенціал взаємодії (а не поле). Для побудови потенційного представлення\(\overline {E}\) і\(\overline {B}\), потрібен векторний потенціал\(\overline {A} ( \overline {r} , t )\) і скалярний потенціал\(\varphi ( \overline {r} , t )\). Для електростатики ми зазвичай думаємо, що поле пов'язане з електростатичним потенціалом через\(\overline {E} = - \nabla \varphi\), але для поля, яке змінюється в часі та просторі, електродинамічний потенціал повинен бути виражений як\(\overline {A}\) і\(\varphi\).

Загалом, електромагнітна хвиля, написана з точки зору електричного та магнітного полів, вимагає шести змінних (та\(x\)\(y\),\(E\) і\(z\) компонентів і\(B\)). Це надмірно визначена задача; рівняння Максвелла обмежують їх. Потенційне представлення має чотири змінні (\(A _ {x}\)\(A _ {y}\)\(A _ {z}\),, і\(\varphi\)), але вони все ще не однозначно визначені. Ми вибираємо обмеження - представлення або калібр - що дозволяє нам однозначно описати хвилю. Вибір такого калібру, який\(\varphi=0\) (тобто кулонівський калібр) призводить до унікального опису\(\overline {E}\) і\(\overline {B}\):

\[- \overline {\nabla}^{2} \overline {A} ( \overline {r} , t ) + \frac {1} {c^{2}} \frac {\partial^{2} \overline {A} ( \overline {r} , t )} {\partial t^{2}} = 0 \label{6.4}\]

і

\[\overline {\nabla} \cdot \overline {A} = 0 \label{6.5)}\]

Це хвильове рівняння для векторного потенціалу дає плоский хвильовий розв'язок для вільного простору заряду та відповідних граничних умов:

\[\overline {A} ( \overline {r} , t ) = A _ {0} \hat {\varepsilon} e^{i ( \overline {k} \cdot \overline {r} - \omega t )} + A _ {0}^{*} \hat {\varepsilon} e^{- i ( \overline {k} \cdot \overline {r} - \omega t )} \label{6.6}\]

Це описує коливається в часі хвиля з кутовою частотою\(\omega\) і поширюється в просторі в напрямку вздовж хвильового вектора\(\overline {k}\), з просторовим періодом\(\lambda = 2 \pi / | \overline {k} |\). Написання співвідношення між\(k\)\(\omega\), і\(\lambda\) в середовищі з індексом заломлення\(n\) в терміні їх значень у вільному просторі:

\[k = n k _ {0} = \frac {n \omega _ {0}} {c} = \frac {2 \pi n} {\lambda _ {0}} \label{6.7}\]

Хвиля має амплітуду\(A_0\), яка спрямована уздовж вектора одиниці поляризації\(\overline {k}\). З тих пір\(\overline {\nabla} \cdot \overline {A} = 0\), ми бачимо, що\(\overline {k} \cdot \hat {\mathcal {E}} = 0\) або\(\overline {k} \perp \hat {\mathcal {E}}\). З векторного потенціалу ми можемо отримати\(\overline {E}\) і\(\overline {B}\)

\[\begin{align} \overline {E} & = - \frac {\partial \overline {A}} {\partial t} \\[4pt] & = i \omega A _ {0} \hat {\varepsilon} \left( e^{i ( \overline {k} \cdot \overline {r} - \omega t )} - e^{- i ( \overline {k} \cdot \overline {r} - \omega t )} \right) \label{6.8} \end{align}\]

\[ \begin{align} \overline {B} & = \overline {\nabla} \times \overline {A} \\[4pt] & = i ( \overline {k} \times \hat {\varepsilon} ) A _ {0} \left( e^{i ( \overline {k} \cdot \overline {r} - \omega t )} - e^{- i ( \overline {k} \cdot \overline {r} - \omega t )} \right) \label{6.9} \end{align}\]

Якщо визначити одиничний вектор вздовж поляризації магнітного поля як

\[\hat {b} = ( \overline {k} \times \hat {\mathcal {\varepsilon}} ) / | \overline {k} | = \hat {k} \times \hat {\mathcal {E}},\]

ми бачимо, що хвильовий вектор, поляризація електричного поля і поляризація магнітного поля взаємно ортогональні\(\hat {k} \perp \hat {\varepsilon} \perp \hat {b}\).

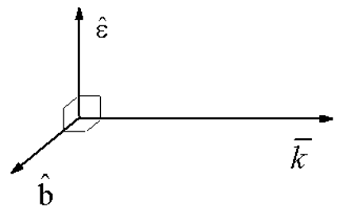
Крім того, порівнюючи Equation\ ref {6.6} та\ ref {6.8}, ми бачимо, що векторний потенціал коливається як\(\cos(\omega t)\), тоді як електричне та магнітне поля коливаються як\(\sin(\omega t)\). Якщо ми визначимо

\[\frac {1} {2} E _ {0} = i \omega A _ {0} \label{6.10}\]

\[\frac {1} {2} B _ {0} = i | k | A _ {0} \label{6.11}\]

потім,

\[\overline {E} ( \overline {r} , t ) = \left| E _ {0} \right| \hat {\varepsilon} \sin ( \overline {k} \cdot \overline {r} - \omega t ) \label{6.12}\]

\[\overline {B} ( \overline {r} , t ) = \left| B _ {0} \right| \hat {b} \sin ( \overline {k} \cdot \overline {r} - \omega t ) \label{6.13}\]

Зверніть увагу, що

\[E _ {0} / B _ {0} = \omega / | k | = c.\]

Ми хочемо висловити амплітуду поля таким чином, який є експериментально доступним. Інтенсивність\(I\), потік енергії через одиницю площі, найбільш легко виміряти. Це усереднене за часом значення вектора Пойнтінга

\[I = \langle \overline {S} \rangle = \frac {1} {2} \varepsilon _ {0} c E _ {0}^{2} \quad \left( \mathrm {W} / \mathrm {m}^{2} \right) \label{6.15}\]

Альтернативним поданням амплітуди, яка корисна для опису квантових світлових полів, є щільність енергії.

\[U = \frac {I} {c} = \frac {1} {2} \varepsilon _ {0} E _ {0}^{2} \quad \left( \mathrm {J} / \mathrm {m}^{3} \right) \label{6.16}\]

Класичний гамільтоніан для поля випромінювання, що взаємодіє із зарядженою частинкою

Тепер ми отримуємо класичний гамільтоніан, який описує заряджені частинки, що взаємодіють з полем випромінювання через векторний потенціал. Почніть з сили Лоренца на частку з зарядом\(q\):

\[\overline {F} = q ( \overline {E} + \overline {v} \times \overline {B} ) \label{6.17}\]

Тут v - швидкість частинки. Записуючи це для одного напрямку (\(x\)) з точки зору декартових компонентів\(\overline {E}\)\(\overline {v}\), і\(\overline {B}\), ми маємо:

\[F _ {x} = q \left( E _ {x} + v _ {y} B _ {z} - v _ {z} B _ {y} \right) \label{6.18}\]

У механіці Лагранжа ця сила може бути виражена через загальну потенційну енергію

\[F _ {x} = - \frac {\partial U} {\partial x} + \frac {d} {d t} \left( \frac {\partial U} {\partial v _ {x}} \right) \label{6.19}\]

Використовуючи зв'язки, які описують\(\overline {E}\) і\(\overline {B}\) через\(\overline {A}\) і\(\varphi \) (Рівняння\ ref {6.10} і\ ref {6.11}), вставляючи в рівняння\ ref {6.18}, і працюючи з ним у вигляді Рівняння\ ref {6.19}, ми можемо показати, що

\[U = q \varphi - q \overline {v} \cdot \overline {A} \label{6.20}\]

Це отримано в іншому місці ⁴ і легко підтверджується заміною його на Equation\ ref {6.19}. Тепер ми можемо написати Лагранжа з точки зору кінетичної та потенційної енергії частинки.

\[\begin{align} L &= T - U \label{6.21} \\[4pt] &= \frac {1} {2} m \overline {v}^{2} + q \overline {v} \cdot \overline {A} - q \varphi \label{6.22} \end{align}\]

Класичний гамільтоніан пов'язаний з лагранжевим як

\[\begin{align} H & = \overline {p} \cdot \overline {v} - L \\[4pt] & = \overline {p} \cdot \overline {v} - \frac {1} {2} m \overline {v}^{2} - q \overline {v} \cdot \overline {A} - q \varphi \label{6.23} \end{align}\]

Визнання

\[\overline {p} = \frac {\partial L} {\partial \overline {v}} = m \overline {v} + q \overline {A} \label{6.24}\]

пишемо

\[\overline {v} = \frac {1} {m} ( \overline {p} - q \overline {A} ) \label{6.25}\]

Тепер підставляючи рівняння\ ref {6.25} в рівняння\ ref {6.23}, ми маємо

\[ \begin{align} H &= \frac {1} {m} \overline {p} \cdot ( \overline {p} - q \overline {A} ) - \frac {1} {2 m} ( \overline {p} - q \overline {A} )^{2} - \frac {q} {m} ( \overline {p} - q \overline {A} ) \cdot A + q \varphi \label{6.26} \\[4pt] &= \frac {1} {2 m} [ \overline {p} - q \overline {A} ( \overline {r} , t ) ]^{2} + q \varphi ( \overline {r} , t ) \label{6.27} \end{align}\]

Це класичний гамільтоніан для частинки в електромагнітному полі. У кулонівському\(\varphi = 0\) калібрі () останній термін скидається.

Ми можемо записати гамільтоніан для однієї частинки в зв'язаному\(V_0\) потенціалі за відсутності зовнішнього поля як

\[H _ {0} = \frac {\overline {p}^{2}} {2 m} + V _ {0} ( \overline {r} ) \label{6.28}\]

і при наявності ЕМ-поля,

\[H = \frac {1} {2 m} ( \overline {p} - q \overline {A} ( \overline {r} , t ) )^{2} + V _ {0} ( \overline {r} ) \label{6.29}\]

Розширюємо отримуємо

\[H = H _ {0} - \frac {q} {2 m} ( \overline {p} \cdot \overline {A} + \overline {A} \cdot \overline {p} ) + \frac {q^{2}} {2 m} | \overline {A} ( \overline {r} , t ) |^{2} \label{6.30}\]

Як правило, останній термін, який йде як квадрат, невеликий порівняно з перехресним терміном, який пропорційний першій владі\(A\).\(A\) Цей термін слід розглядати для надзвичайно високої напруженості поля, яка є незбуреною і значно спотворює потенційні зв'язки молекул між собою, тобто коли вона за величиною схожа на\(V_0\). Можна оцінити, що це почне відігравати певну роль на рівнях інтенсивності\(>10^{15}\, W/cm^2\), які можуть спостерігатися для дуже високої енергії та щільно сфокусованих імпульсних фемтосекундних лазерів. Отже, для слабких полів у нас є вираз, який відображає безпосередньо на розв'язки, які ми можемо сформулювати в картині взаємодії:

\[H = H _ {0} + V (t) \label{6.31}\]

із

\[V (t) = \frac {q} {2 m} ( \overline {p} \cdot \overline {A} + \overline {A} \cdot \overline {p} ) \label{6.32}.\]

Читання

1. Коен-Таннуджі, К.; Діу, Б.; Лале, Ф., Квантова механіка. Вілі-Міжнаукові: Париж, 1977; Додаток III.
2. Джексон, Дж., Класична електродинаміка. 2-е видання; Джон Уайлі і сини: Нью-Йорк, 1975.
3. Макхейл, Дж. Л., Молекулярна спектроскопія. 1-е видання; Прентіс Холл: Верхня річка Сідла, Нью-Джерсі, 1999.
4. Мерцбахер, Е., Квантова механіка. 3-е видання; Вілі: Нью-Йорк, 1998.
5. Сакурай, Дж., Сучасна квантова механіка, переглянуте видання. Еддісон-Уеслі: Читання, Массачусетс, 1994.
6. Шац, Г.К.; Ратнер, М.А., Квантова механіка в хімії. Довер Публікації: Мінеола, Нью-Йорк, 2002; стор. 82-83.