6.1: Наближення Борна—Оппенгеймера

В якості відправної точки корисно переглянути наближення Борна — Оппенгеймера (BOA). Для молекулярної системи гамільтоніан можна записати через кінетичну енергію ядер (\(N\)) та електронів () та потенційну енергію для кулонівських взаємодій цих частинок.\(e\)

\[\begin{align} \hat {H} = \hat {T} _ {e} + \hat {T} _ {N} + \hat {V} _ {e e} + \hat {V} _ {N N} + \hat {V} _ {e N} \\[4pt] = - \sum _ {i = 1}^{n} \frac {\hbar^{2}} {2 m _ {e}} \nabla _ {i}^{2} - \sum _ {J = 1}^{N} \frac {\hbar^{2}} {2 M _ {J}} \nabla _ {J}^{2} \\[4pt] = - \sum _ {i = 1}^{n} \frac {\hbar^{2}} {2 m _ {e}} \nabla _ {i}^{2} - \sum _ {J = 1}^{N} \frac {\hbar^{2}} {2 M _ {J}} \nabla _ {J}^{2} \label{5.1} \end{align}\]

Тут і в наступному, ми будемо використовувати малі змінні для позначення електронів, а великі регістри - до ядер. Змінні\(n\)\(i\),\(\mathbf {r}\),\(\nabla _ {r}^{2}\),, і\(m_e\) відносяться до числа, індексу, положення, лапласа, і маси електронів, відповідно, і\(N\)\(J\),\(\mathbf {R}\),, і\(M\) відносяться до ядер. \(e\)є зарядом електронів, і\(Z\) є атомним номером ядра. Зверніть увагу, цей гамільтоніан не включає релятивістські ефекти, такі як спін-орбітальна зв'язок.

Незалежне від часу рівняння Шредінгера

\[\hat {H} ( \hat {\mathbf {r}} , \hat {\mathbf {R}} ) \Psi ( \hat {\mathbf {r}} , \hat {\mathbf {R}} ) = E \Psi ( \hat {\mathbf {r}} , \hat {\mathbf {R}} ) \label{5.2}\]

\(\Psi ( \hat {\mathbf {r}} , \hat {\mathbf {R}} )\)це загальна вібронічна хвильова функція, де «вібронік» відноситься до комбінованих електронних і ядерних власних станів. Точні розв'язки з використанням молекулярного гамільтоніана є нерозв'язними для більшості проблем, що цікавлять, тому ми переходимо до спрощення наближень. Наближення БО мотивоване тим, що ядра набагато масивніші, ніж електрон (\(m_e \ll M_I\)). При цьому критерії, і коли відстані, що розділяють частинки, не надзвичайно малі, кінетична енергія ядер невелика щодо інших термінів у гамільтоніана. Фізично це означає, що електрони рухаються і швидко адаптуються - адіабатично - у відповідь на зміщення ядерних позицій. Це пропонує шлях до вирішення для\(\Psi\) шляхом фіксації положення ядер, вирішення для електронних хвильових функцій\(\psi_i\), а потім ітерації для зміни для\(\boldsymbol {R}\) отримання ефективних електронних потенціалів, на яких рухаються ядра.

Так як він закріплений для електронного розрахунку, ми приступимо до\(\mathbf {R}\) розгляду як параметра, а не оператора, встановленого\(\hat{T}_N\) в 0, і вирішуємо електронний ТІСЕ:

\[\hat {H} _ {e l} ( \hat {\mathbf {r}} , \mathbf {R} ) \psi _ {i} ( \hat {\mathbf {r}} , \mathbf {R} ) = U _ {i} ( \mathbf {R} ) \psi _ {i} ( \hat {\mathbf {r}} , \mathbf {R} ) \label{5.3}\]

\(U_i\)є власними значеннями електронної енергії для фіксованих ядер, а електронний гамільтоніан у наближенні БО є

\[\hat {H} _ {e l} = \hat {T} _ {e} + \hat {V} _ {e e} + \hat {V} _ {e N} \label{5.4}\]

У Equation\ ref {5.3},\(\psi_i\) це електронна хвильова функція для фіксованого\(\mathbf {R}\), з\(i = 0\) посиланням на електронний стан заземлення. Повторюючи цей розрахунок для змінного\(\mathbf {R}\)\(U_i(R)\), ми отримаємо ефективний або середній потенціал для електронних станів, за якими можуть рухатися ядра. Ці ефективні потенціали відомі як Борн-Оппенгеймер або адіабатичні потенційні енергетичні поверхні (PES).

Для ядерних ступенів свободи ми можемо визначити гамільтоніан для ^{електронного} PES:,

\[\hat {H} _ {N u c , i} = \hat {T} _ {N} + U _ {i} ( \hat {R} ) \label{5.5}\]

який задовольняє ТІСЕ для функцій ядерної хвилі\(\Phi(R)\):

\[\hat {H} _ {N u c , i} \Phi _ {i J} ( R ) = E _ {i J} \Phi _ {i J} ( R ) \label{5.6}\]

Тут\(J\) йдеться про J - ^{власний} стан для ядер, що розвиваються на них i PES. Рівняння\ ref {5.5} називається BO гамільтоніаном.

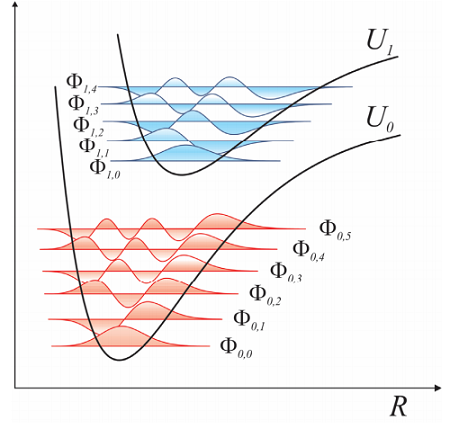
BOA ефективно розділяє ядерний та електронний внесок у хвильову функцію, дозволяючи нам висловити загальну хвильову функцію як добуток цих внесків

\[\Psi ( \mathbf {r} , \mathbf {R} ) = \Phi ( \mathbf {R} ) \psi ( \mathbf {r} , \mathbf {R} )\]та власні значення як суми над електронним та ядерним внеском:

\(E = E _ {N} + E _ {e}.\)BOA не лікує ядра класично. Однак він є основою для методів напівкласичної динаміки, при яких ядра еволюціонують класично на потенційній енергетичній поверхні і взаємодіють з квантово-електронними станами. Якщо ми ставимося до ядерної динаміки класично, то електронний гамільтоніан можна розглядати як залежний від часу\(\mathbf {R}\) або від часу як пов'язаний швидкістю або моментом. Якщо ядра рухаються нескінченно повільно, електрони адіабатично слідуватимуть за ядрами, а системи, підготовлені в електронному власному стані, залишаться у цьому власному стані протягом усіх часів.