1.4: Експоненціальні оператори

Протягом усієї нашої роботи ми будемо використовувати експоненціальні оператори форми

\[\hat {T} = e^{- i \hat {A}} \label{115}\]

Ми побачимо, що ці експоненціальні оператори діють на хвильову функцію, щоб переміщати її у часі та просторі, і тому їх також називають пропагандаторами. Особливий інтерес для нас представляє оператор часової еволюції,\(\hat {U} = e^{- i \hat {H} t / \hbar},\) який поширює хвильову функцію в часі. Зверніть увагу,\(\hat{T}\) що оператор є функцією оператора,\(f(\hat{A})\). Функція оператора визначається шляхом її розширення в ряді Тейлора, наприклад

\[\hat {T} = e^{- \hat {i} \hat {A}} = \sum _ {n = 0}^{\infty} \dfrac {( - i \hat {A} )^{n}} {n !} = 1 - i \hat {\hat {A}} - \dfrac {\hat {A} \hat {A}} {2} - \cdots \label{116}\]

Оскільки ми використовуємо їх так часто, давайте розглянемо властивості експоненціальних операторів, які можна встановити за допомогою Equation\ ref {116}. Якщо оператор\(\hat {A}\) Ерміт, то\(\hat {T} = e^{- i \hat {A}}\) є унітарним, тобто,\(\hat {T}^{\dagger} = \hat {T}^{- 1}.\) Таким чином гермітієвий кон'югат\(\hat {T}\) з змінює дію\(\hat {T}\). Для розповсюджувача часу часто\(\vec {U}^{\dagger}\) називають оператором\(\vec {U}\) часового розвороту.

\(\hat {A}\)Також власні стани оператора є власними станами\(f(\hat {A})\), а власні значення є функціями власних значень\(\hat {A}\). А саме, якщо ви знаєте власні значення і власні вектори\(\hat {A}\), тобто\(\hat {A} \varphi _ {n} = a _ {n} \varphi _ {n},\) ви можете показати, розгорнувши функцію

\[f ( \hat {A} ) \varphi _ {n} = f \left( a _ {n} \right) \varphi _ {n} \label{117}\]

Наше найпоширеніше застосування цієї властивості буде до експоненціальних операторів за участю гамільтоніана. З огляду на власні стани\(\varphi _ {n}\), то\(\hat {H} | \varphi _ {n} \rangle = E _ {n} | \varphi _ {n} \rangle\) мається на увазі

\[e^{- i \hat {H} t / \hbar} | \varphi _ {n} \rangle = e^{- i E _ {n} t / \hbar} | \varphi _ {n} \rangle \label{118}\]

Так само, як\(\hat {D} _ {x} ( \lambda )\) і оператор часової еволюції, який витісняє хвильову функцію в часі,\(\hat {D} _ {x} = e^{- i \hat {p} _ {x} x / h}\) є оператором просторового переміщення, який рухається\(\psi\) уздовж\(x\) координати. Якщо ми визначимо,\(\hat {D}_ {x} = e^{- i \hat {p} _ {x} x / h},\) то дія полягає в зміщенні хвильової функції на величину\(\lambda\)

\[| \psi ( x - \lambda ) \rangle = \hat {D} _ {x} ( \lambda ) | \psi (x) \rangle \label{119}\]

Також, звернення\(\hat {D} _ {x} ( \lambda )\) до посади оператор зміщує оператора на\(\lambda\)

\[\hat {D} _ {x}^{\dagger} \hat {x} \hat {D} _ {x} = x + \lambda \label{120}\]

Таким чином,\(e^{- i \hat {p} _ {x} \lambda / \hbar} | x \rangle\) є власним\(\hat {x}\) вектором з власним значенням\(x + \lambda\) замість\(x\). Оператор

\(\hat {D} _ {x} = e^{- i \hat {p} _ {x} \lambda / h}\)оператор переміщення координат\(x\) положення. Аналогічним чином\(\hat {D} _ {y} = e^{- i \hat {p} _ {y} \lambda / h}\) генерує переміщення в\(y\) і\(\hat {D_z}\) в\(z\). Подібно до тимчасового пропагатора\(\boldsymbol {U}\), оператор переміщення\(\boldsymbol {D}\) повинен бути унітарним, так як дія\(\hat {D}^{\dagger} \hat {D}\) повинна залишити систему незмінною. Тобто якщо\(\hat {D} _ {x}\) зсуває систему на\(x\) з\(x_0\), то\(\hat {D} _ {x}^{\dagger}\) зміщує систему зі\(x\) спини на\(x_0\).

Малюнок\(\PageIndex{1}\)

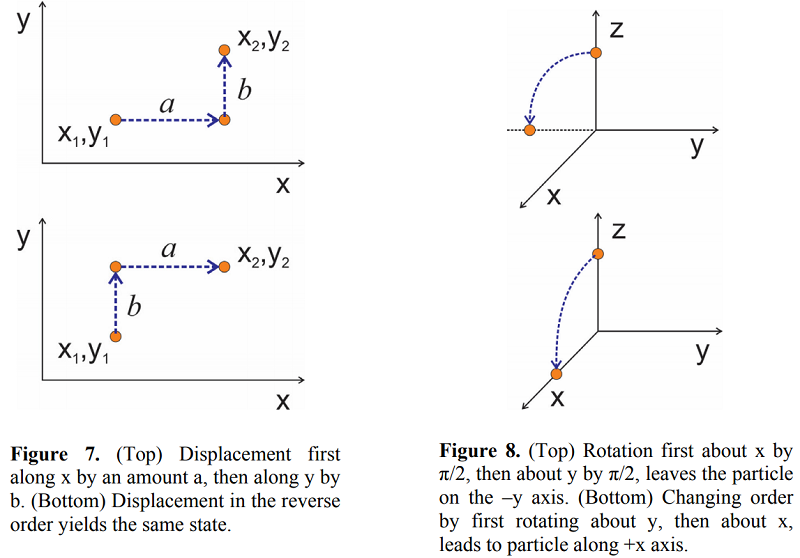
Ми інтуїтивно знаємо, що лінійні переміщення комутують. Наприклад, якщо ми хочемо зрушити частку в двох вимірах, x і y, порядок переміщення не має значення. Ми в кінцевому підсумку в тому ж положенні, незалежно від того, рухаємося ми вздовж x спочатку або вздовж y, як показано на малюнку 7. З точки зору операторів переміщення, ми можемо написати

\ [\ почати {вирівняний}
\ вліво |x_ {2}, y_ {2}\ праворуч\ діапазон &=e^ {-i b p_ {y}/\ hbar} e^ {-i a p_ {x}/\ hbar}\ вліво |x_ {1}, y_ {1}\ праворуч\ діапазон\\
&= e^ {-i p_ {x}/\ hbar} e^ {-i b p_ {y}/\ hbar}\ ліворуч |x_ {1}, y_ {1}\ праворуч\ діапазон
\ кінець {вирівняний}\]

Ці оператори переміщення їздять на роботу, як і очікувалося від\([p_x,p_y] = 0.\)

Подібно до оператора переміщення, ми можемо визначити оператори обертання, які залежать від операторів кутового моменту\(L_x\),\(L_y\), і\(L_z\). Наприклад,

\[\hat {R} _ {x} ( \phi ) = e^{- i \phi L _ {x} / \hbar}\]

дає поворот на кут\(\phi\) навколо\(x\) осі. На відміну від лінійного переміщення, обертання навколо різних осей не коммутують. Наприклад, розглянемо стан, що представляє частинку, зміщену вздовж осі z,\(| z 0 \rangle\). Тепер дія двох обертань\(\hat {R} _ {x}\) і\(\hat {R} _ {y}\) кутом\(\phi = \pi / 2\) на цю частку відрізняється в залежності від порядку роботи, як показано на малюнку 8. Якщо ми обертаємо спочатку про\(x\), операція

\[e^{- i \tfrac {\pi} {2} L _ {y} / \hbar} e^{- i \tfrac {\pi} {2} L _ {x} / \hbar} | z _ {0} \rangle \rightarrow | - y \rangle \label{122}\]

призводить до частинки на осі —y, тоді як зворотний порядок

\[e^{- i \tfrac {\pi} {2} L _ {x} / \hbar} e^{- i \tfrac {\pi} {2} L _ {y} / \hbar} | z _ {0} \rangle \rightarrow | + x \rangle \label{123}\]

призводить до частинки на осі+х. Кінцевий стан цих двох обертань, прийнятих в протилежному порядку, відрізняються обертанням навколо осі z. Оскільки обертання навколо різних осей не коммутіруют, ми очікуємо, що оператори кутового моменту не будуть їздити на роботу. Дійсно, ми знаємо, що

\[\left[ L _ {x} , L _ {y} \right] = i \hbar L _ {z}\]

де комутатор обертань навколо осей x і y пов'язаний обертанням осі z. Як і у випадку з операторами обертання, нам потрібно бути обережними з розповсюджувачами часу, щоб визначити, чи має значення порядок поширення часу. Це, в свою чергу, буде залежати від того, чи будуть гамільтонці в два моменти часу їздити на роботу.

Властивості експоненціальних операторів

1. Якщо\(\hat{A}\) і\(\hat{B}\) не їздити на роботу, а\([ \hat {A} , \hat {B} ]\) їздити з\(\hat{A}\) і\(\hat{B}\), то

\[e^{\hat {A} + \hat {B}} = e^{\hat {A}} e^{\hat {B}} e^{- \frac {1} {2} [ \hat {A} , \hat {B} ]} \label{124}\]

\[e^{\hat {A}} e^{\hat {B}} = e^{\hat {B}} e^{\hat {A}} e^{- [ \hat {B} , \hat {A} ]} \label{125}\]

2. Більш загально, якщо\(\hat{A}\) і\(\hat{B}\) не доїхати,

\[ e^{\hat {A}} e^{\hat {B}} = {\mathrm {exp}} \left[ \hat {A} + \hat {B} + \dfrac {1} {2} [ \hat {A} , \hat {B} ] + \dfrac {1} {12} ( [ \hat {A} , [ \hat {A} , \hat {B} ] ] + [ \hat {A} , [ \hat {B} , \hat {B} ] ] ) + \cdots \right] \label{126}\]

3. Відносини Бейкер - Хаусдорф:

\[\left. \begin{array} {r l} {\mathrm {e}^{i \hat {G} \lambda} \hat {A} \mathrm {e}^{- i \hat {G} \lambda} = \hat {A} + i \lambda [ \hat {G} , \hat {A} ] + \left( \dfrac {i^{2} \lambda^{2}} {2 !} \right) [ \hat {G} , [ \hat {G} , \hat {A} ] ] + \ldots} \\ {} & {+ \left( \dfrac {i^{n} \lambda^{n}} {n !} \right) [ \hat {G} , [ \hat {G} , [ \hat {G} , \hat {A} ] ] ] \ldots ] + \ldots} \end{array} \right. \label{127}\]

де\(λ\) - число.