1.2: Квантово-механічна модель атома
- Page ID
- 18364
Дуалізм хвильових частинок
Явище хвильово-частинкового дуалізму було вперше виявлено для електромагнітного випромінювання, і поширюється на всі інші частинки, включаючи електрон. Почалося з дослідження фотоефекту Альбертом Ейнштейном (рис. 1.2.1 і рис.1.2.2).

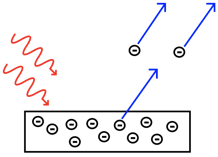
Фотоелектричний ефект виникає при опроміненні металевої поверхні світлом. Вище певної частоти, або нижче певної довжини хвилі, світло здатний викидати електрони з поверхні металу. Порогова частота залежить від металу. Нижче порогової частоти жодні електрони не викидаються. Ейнштейн досліджував максимальну кінетичну енергію викинутих електронів в залежності від частоти світла. Він виявив, що існує лінійна залежність. Він проаналізував нахил цієї лінії і виявив, що нахил є постійною Планка h Це означало б, що електрони мали енергію Е = H\(\nu\) мінус енергія E B, яка буде потрібна для подолання енергії зв'язку, також званої робочою функцією, електрона в металі (рис. 1.2.3, зліва).
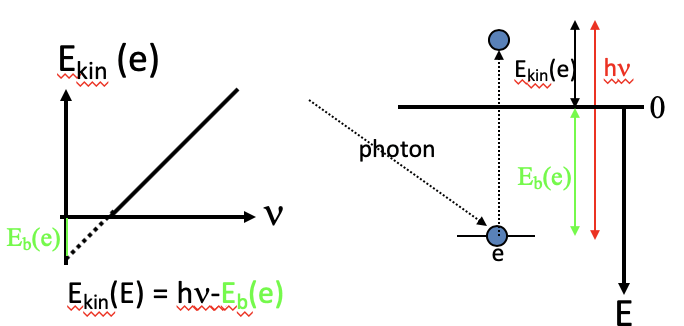
Рівняння Е = h раніше\(\nu\) було виведено Планком (рис. 1.2.4) на основі припущення, що енергія квантована, і тепер Ейнштейн експериментально знайшов це знову в пошуках пояснення фотоелектричного ефекту. Це означало б, що світло квантували. Квантування пояснюється тим, що світло матиме не тільки хвильові, але й властивості частинок, і ці частинки називатимуться фотонами. Припускаючи, що фотони фотоелектричний ефект можна легко пояснити (рис. 1.2.3, праворуч). При попаданні світла на поверхню металу фотон стикається з електроном. Тільки коли фотон мав енергію більше, ніж робоча функція металу, електрон викидався б і мав кінетичну енергію, рівну різниці між енергією фотона і енергією зв'язку. Хвильово-частинковий дуалізм світла та електромагнітного випромінювання взагалі також може бути математично виведений. Оскільки маса може бути перетворена в електромагнітне випромінювання відповідно до рівняння E = mc 2, а енергія електромагнітного випромінювання E=h\(\nu\), mc 2 = h\(\nu\). Ми можемо вирішити рівняння для\(\nu\), і тоді це\(\nu\) = mc 2 /h. З\(\nu\) = c/λ, і вирішується для λ, рівняння стає λ=h/mc. Це рівняння показує хвильову частинку-дуалізм електромагнітного випромінювання, оскільки воно пов'язує довжину хвилі до маси. Насправді маса частинки, пов'язаної з електромагнітним випромінюванням, фотона, обернено пропорційна довжині хвилі електромагнітного випромінювання. Відкриття хвильово-частинкового дуалізму електромагнітного випромінювання було кардинально новою концепцією, яку важко зрозуміти інтелектуально до цієї дати, оскільки людський розум прагне бачити хвилі та частинки, щоб бути взаємовиключними. Однак це один з найбільш основоположних принципів природи. Як ми побачимо пізніше, не тільки електромагнітне випромінювання показує дуалізм хвильових частинок, але і всі частинки, включаючи електрони.

Дуалізм хвильових частинок масивних частинок
Дуалізм хвильових частинок спочатку вважався дійсним лише для фотона. Молодий французький аспірант з фізики Луї Де Брольє мав радикальну ідею, що не тільки фотон, але і всі частинки будуть проявляти дуалізм хвильових частинок, включаючи електрон. Формула Ейнштейна λ = h/mc просто потрібно буде трохи переставити в λ = h/mv, в результаті чого m буде масою частинки, а v - швидкість частинки. Ця ідея була багато спірною в той час, і кандидатська дисертація Луї де Бройля майже не була прийнята. Однак врешті-решт хвильово-частинковий дуалізм електрона був доведений експериментами з дифракції електронів, а Луї Де Брольє був удостоєний Нобелівської премії в 1929 році. Сьогодні ми вважаємо, що всі частинки показують хвильово-частинковий дуалізм, і жоден експеримент до цієї дати не вказує на виняток.

стоячі хвилі
З відкриттям хвильово-частинкового дуалізму електрона і спостереженням квантування електронних станів в атомах змусили фізиків зосередитися на полі фізики, в якому квантуються хвилі. Поле стоячих хвиль (рис.1.2.6).
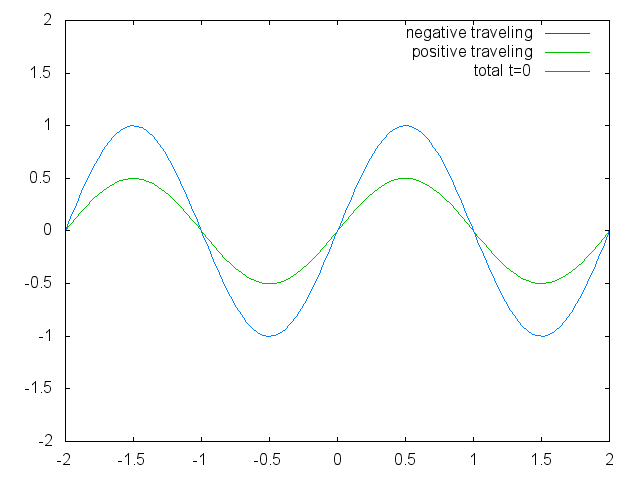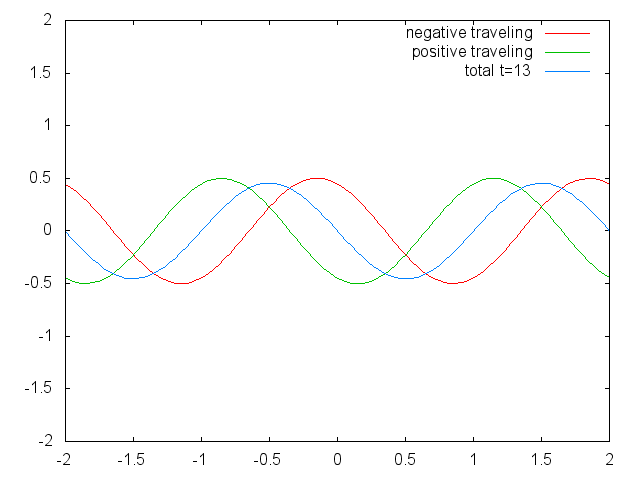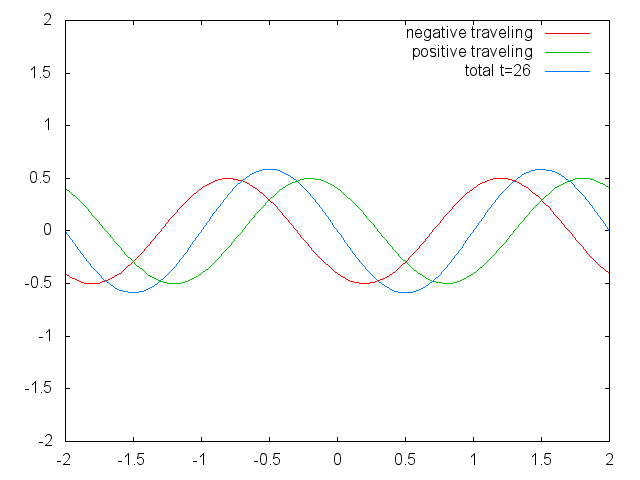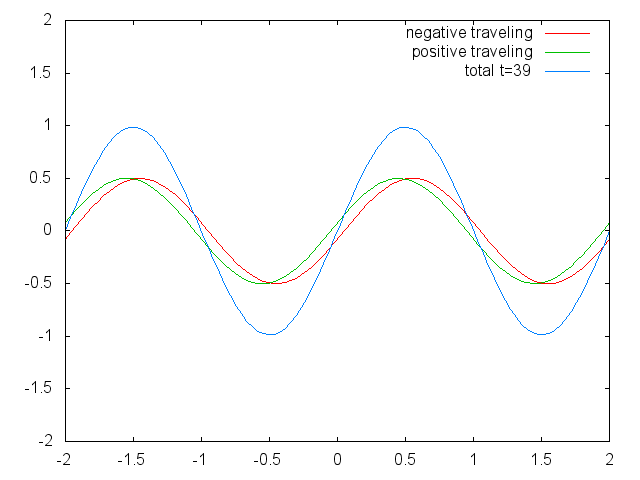
Малюнок 1.2.6 Дві обмежені біжучі хвилі (червона і зелена), що виробляють стоячу хвилю (синю) через їх втручання. (Зазначення Авторства: Зазначення Авторства: [CC BY-SA (https://creativecommons.org/licenses/by-sa/3.0)], Commons.wikimedia.org/wiki/f... _animation.gif)
Стоячі хвилі - досить поширене явище. Наприклад, ви можете викликати стоячі хвилі, вищипуючи гітарну струну. Це призводить до того, що гітарна струна вібрує в стоячих хвиль з дискретними квантованими довжинами хвиль. Вібрація з найдовшою довжиною хвилі - це так звана вібрація землі. Його довжина хвилі в два рази перевищує довжину гітарної струни. Крім того, можливі так звані вищі гармоніки. Перша гармоніка має довжину хвилі, рівну довжині гітарної струни, друга - має довжину хвилі, рівну двом третинам довжини струни, третя має довжину хвилі, рівну половині довжини струни, четверта має довжину хвилі, рівну третині довжини гітари струна, і так четверта (рис.1.2.7).
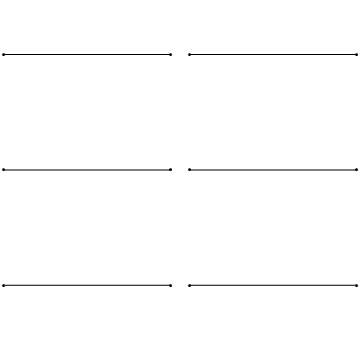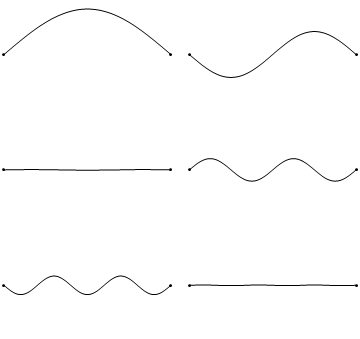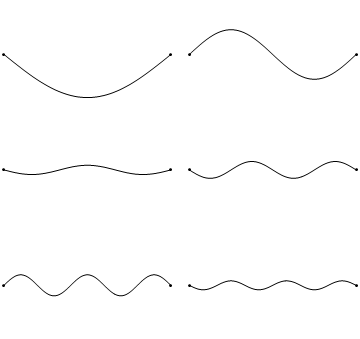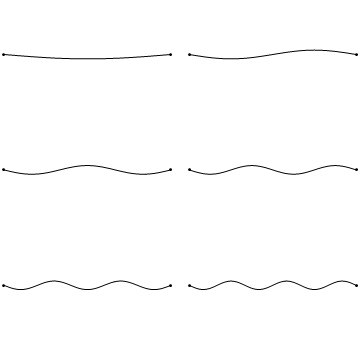
Можна легко помітити, що можливі довжини хвиль, на яких струна може вібрувати, слідують рівнянню λ=2L/n, при якому n - ціле число, або квантове число, а L - довжина гітарної струни. Таким чином, можна сказати, що хвилі, пов'язані з вібраціями гітарної струни, квантуються. Чому ці хвилі називають стоячими хвилями? Це пояснюється тим, що положення гребенів і жолобів і вузлів не рухаються. Вони залишаються в одному положенні на гітарній струні в будь-який момент часу. Тут слід сказати, що стоячий характер хвиль насправді є ілюзією. На гітарній струні фактично дві хвилі рухаються в протилежному напрямку, і ці хвилі заважають один одному так, що утворюється стояча хвиля (це проілюстровано на рис. 1.2.6). Коли гітарна струна вищипується, дві хвилі направляються в протилежному напрямку на гітарній струні до двох протилежних кінців гітарної струни. Після того, як вони досягли цих кінців, вони відображаються і відправляються в зворотному напрямку, поки вони знову не досягнуть кінців гітарної струни, де вони знову відображаються. Під час цього процесу, який відбувається знову і знову, дві хвилі заважають і виробляють стоячу хвилю. Підсумовуючи, той факт, що хвиля обмежена всередині гітарної струни, призводить до квантованим стоячим хвилям.
Електрон в одновимірній коробці
Дайте нам знати, перейдіть від вібраційної гітарної струни до електрона в одновимірній коробці довжини, що має нескінченно високі стіни. Усередині коробки потенційна енергія електрона дорівнює нулю, в стінках потенційна енергія нескінченна (рис. 1.2.8).
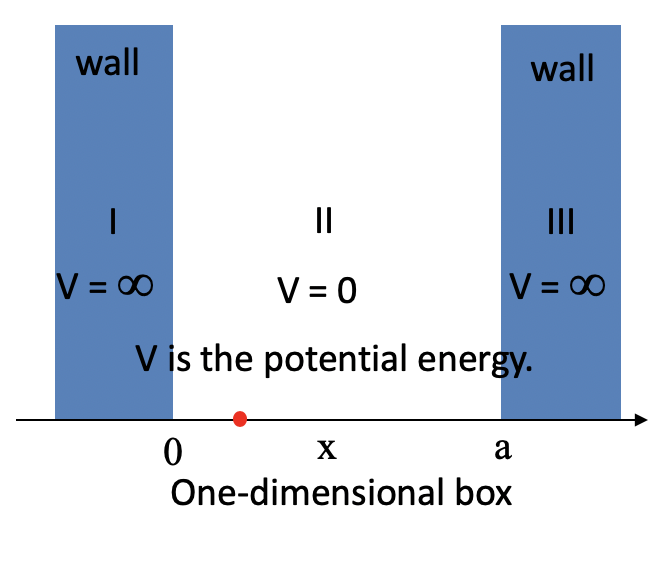
Завдяки своїй кінетичній енергії електрон може переміщатися по лінії всередині коробки, поки не вдариться про стінку (рис. 1.2.9, А). На стіні він відбивається і змушений рухатися в зворотному напрямку, поки він знову не потрапить на стіну, де вона знову змінює напрямок, і так далі. Розглянемо тепер, що електрон має не тільки частинкові, але і хвильові властивості. Через це також хвиля рухається уздовж лінії, відбивається на стіні, рухається в протилежному напрямку, знову відбивається і так далі. Ці хвилі можуть заважати йому іншим, як хвилі, що подорожують по гітарній струні, щоб виробляти стоячу хвилю. Таким чином, електрон в одновимірній коробці повинен вести себе як стояча хвиля, і ця хвиля повинна бути квантована (рис. 1.2.9, В-Ф).
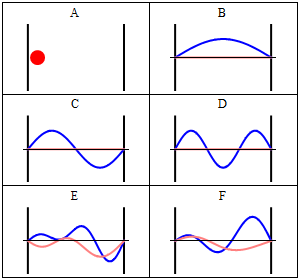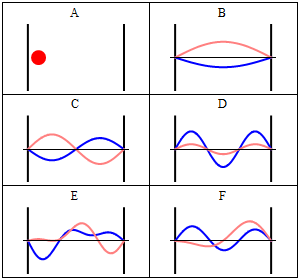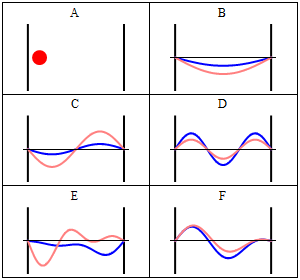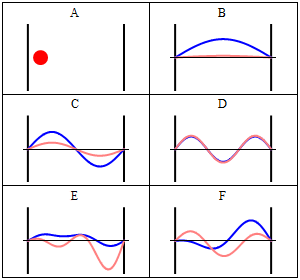
Як математично описати електрон в коробці як стоячу хвилю? Як правило, ви можете описати стоячу хвилю хвильовою функцією. Хвильова функція повідомляє амплітуду стоячої хвилі в певному положенні в одновимірній коробці. Як ми можемо знайти хвильову функцію? Ми можемо почати з диференціального рівняння, яке, як правило, справедливо для стоячих хвиль (ур. 1.2.1).
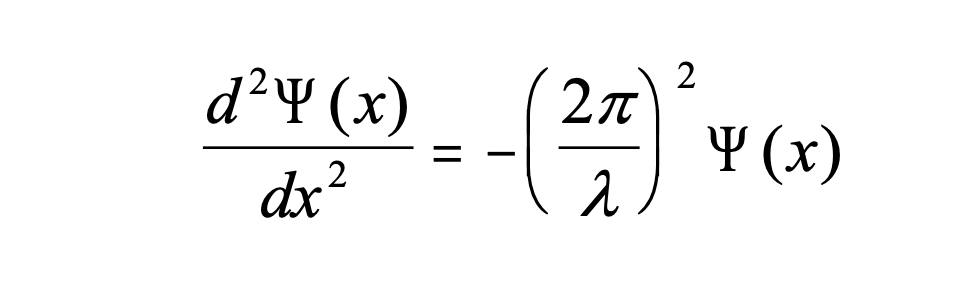
Рівняння 1.2.1 Диференціальне рівняння стоячої хвилі.
У ньому йдеться про те, що друга похідна амплітуди хвильової функції в положенні х дорівнює — (2π/λ) 2, помноженому на амплітуду хвильової функції в положенні х. давайте тепер розглянемо, що кінетична енергія електрона Е = 1/2мВ 2 і розширимо рівняння на m.
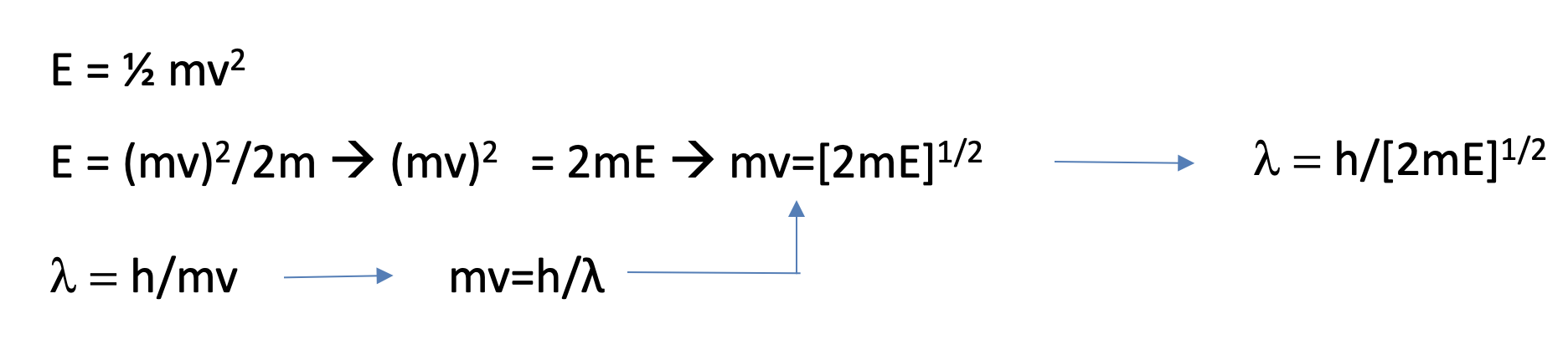
Рівняння 1.2.2 Розв'язування для λ з рівняння кінетичної енергії та рівняння Де Броля.
Давайте потім вирішимо рівняння для (mv). Тепер розв'яжемо рівняння Де Броля для mv і вставимо mv по h/λ в попереднє рівняння. Нарешті, вирішимо рівняння по λ і отримаємо λ = h/ [2Me] 1/2, ур. 1.2.2. Тепер ми можемо підставити λ на h/ [2Me] 1/2 в диференціальному рівнянні. Злегка перебудоване це рівняння стає рівнянням Шредінгера для електрона в одновимірному полі (Рівняння 1.2.3).
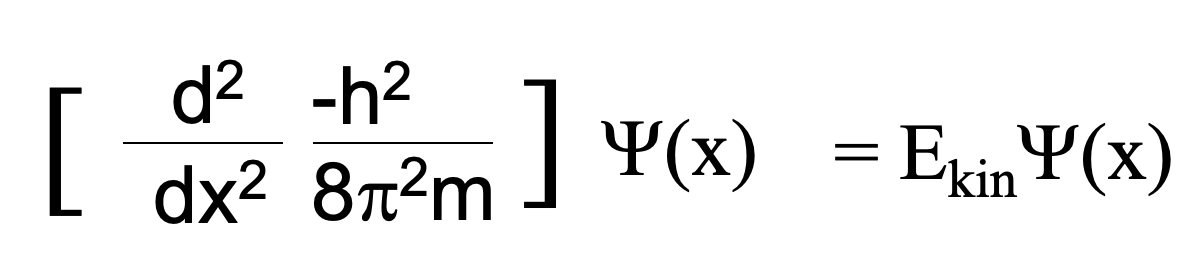
Рівняння 1.2.3 Рівняння Шредінгера для електрона в одновимірному полі.
Рівняння Шредінгера є диференціальним рівнянням. Щоб отримати хвильову функцію, яка описує електрон в коробці, нам потрібно вирішити диференціальне рівняння. Одна з можливостей розв'язання диференціального рівняння полягає в тому, щоб вгадати його рішення, а після цього показати, що рішення правильне. Це той підхід, який ми хочемо дотримуватися тут. Дуже загальна хвильова функція - це сума синусового члена і косинусового члена координати х, за допомогою якого ми будемо приймати два загальні коефіцієнти r і s перед x, і два інших загальних коефіцієнта A і B перед синусом і косинусовим терміном, відповідно.
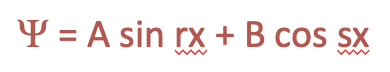
Рівняння 1.2.4 Загальний розв'язок диференціального рівняння.
Тепер ми можемо думати про так звані граничні умови для хвильової функції, які зроблять хвильову функцію більш конкретною. Гранична умова - це властивість хвильова функція повинна бути розумним рішенням диференціального рівняння. Можна припустити першу граничну умову, яка передбачає, що в позиції x=0 амплітуда хвильової функції повинна бути 0. Це можна припустити, оскільки в цих положеннях «електронна хвиля» відбивається на стіні. Це означає, що хвильова функція не може мати косинусовий термін, і тому B повинен бути 0. Якби хвильова функція мала косинусовий термін, вона не була б 0 при x = 0, оскільки косинус 0 не дорівнює 0.
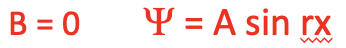
Рівняння 1.2.5 Крайова умова 1 для хвильової функції
Друга гранична умова полягає в тому, що амплітуда хвильової функції дорівнює нулю при x = a. знову ж таки, це тому, що електрон потрапляє на стінку при x = a і змінює свій напрямок. Синусова функція дорівнює лише нулю при x = a, коли ra - ціле число n разів π: ra=nπ. Це означає, що r має бути nπ/a.

Рівняння 1.2.6 Гранична умова 2 для хвильової функції
Таким чином, хвильова функція повинна бути A = sin (nπx/a). Ми бачимо, що хвильова функція, яка описує електрон як стоячу хвилю в одновимірній коробці, квантується, оскільки з'являється квантове число n.

Рівняння 1.2.7 Хвильова функція з урахуванням граничних умов 1 і 2.
Вставка квантових чисел n у хвильові функції виробляє всі стоячі хвилі, які може прийняти електрон (рис.1.2.10). Ви можете бачити, що кількість вузлів і довжини хвиль хвиль залежать від квантового числа n. для n = 0 немає вузла і довжина хвилі в два рази перевищує довжину коробки, для n = 2 є один вузол і довжина хвилі дорівнює довжині коробки, для n =3 є три вузли і довжина хвилі хвиля становить 2/3 довжини коробки і так далі. Ми можемо проілюструвати, що хвильова функція описує хвилі, зображені на малюнку 1.2.10 на прикладі. Амплітуда хвилі для n = 2 дорівнює нулю посередині коробки, де x = a/2. Якщо вставити a/2 в рівняння для ψ, то ψ = A sin (nπ2a/a) = A sin (nπ) = 0, оскільки це властивість синусової функції бути 0 при цілому числі, кратному π. Ми також могли б вставити інші значення для x і n в хвильової функції, і отримати очікувану амплітуду. Це показує, що хвильова функція правильно представляє стоячі хвилі, які може прийняти електрон.
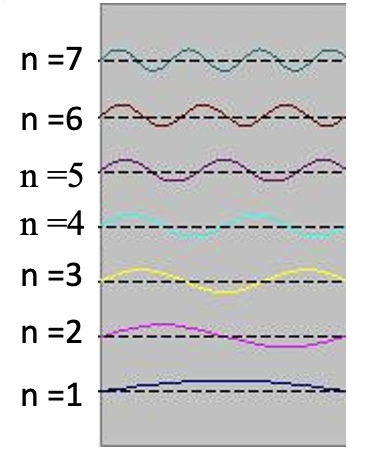
Ми ще не зовсім закінчили з хвильовою функцією, тому що ми не визначили параметр А перед синусовим терміном. Для його отримання нам потрібно розглянути третю граничну умову (ур. 1.2.8).
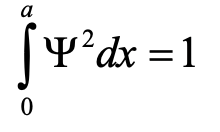
Рівняння 1.2.8 Крайова умова 3.
У ньому йдеться про те, що інтеграл квадрата хвильової функції по довжині коробки повинен дорівнювати одиниці. Ми можемо зрозуміти цю граничну умову, якщо врахувати, що квадрат хвильової функції представляє ймовірність знайти електрон в певному положенні в коробці. Значення, яке квадрат ψ приймає в позиції x всередині коробки, представляє ймовірність знайти електрон в цьому положенні, коли ми розглядаємо електрон як частинку. Це називається інтерпретацією Борна хвильової функції, названої на честь німецького фізика Макса Борна.
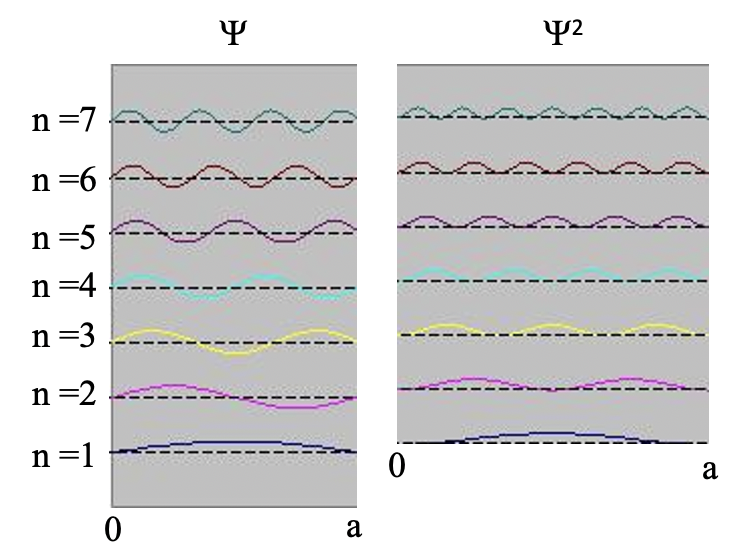
Оскільки ймовірність знайти електрон в будь-якому місці коробки повинна бути 100%, інтеграл квадрата хвильової функції по всій коробці повинен бути 100% або 1. Тут можна показати, і ми опускаємо необхідні математичні кроки для наочності, що гранична умова виконується лише тоді, коли A дорівнює квадратному кореню 2/a, кінцева хвильова функція тоді psi дорівнює 2/a sin (nπx/a). Коефіцієнт квадратний корінь 2/a називається константою нормалізації хвильової функції, оскільки він регулює амплітуду хвильової функції так, що ймовірність знайти електрон в будь-якому місці коробки становить 100%.
Рівняння Шредінгера для атома H
Давайте тепер перейдемо від електрона в 1-мірній коробці до електрона в атомі водню. Що схоже і чим відрізняється між цими двома випадками. Подібність полягає в тому, що електрон обмежений атомом так само, як електрон обмежений у 1D коробці. Таким чином, як і в 1-мірній коробці, електрон повинен вести себе як стояча хвиля. Хоча в одновимірному полі є лише одна координата для розгляду, є три координати, які слід враховувати для електрона в атомі. Це пов'язано з тим, що атом сферичний і, отже, три координати x, y та z необхідні для опису положення всередині атома. Друга велика відмінність полягає в тому, що потенційна енергія електрона дорівнює нулю в будь-якому положенні всередині коробки, в той час як вона не дорівнює нулю в атомі водню. Це відбувається тому, що в атомі є привабливі кулонові сили між ядром і електроном. Чим далі електрон знаходиться від ядра, тим вище його потенційна енергія. Це тому, що потрібна енергія, щоб витягнути електрон від ядра.

Тому нам потрібно змінити рівняння Шредінгера, яке ми використовували раніше для одновимірної коробки наступним чином. По-перше, потрібно розширити оператор кінетичної енергії з одного до трьох вимірів і ввести координати y і z на додаток до x, по-друге, додати до рівняння оператор потенційної енергії. Потенційна енергія - кулонова енергія між протоном і електроном. Він схожий на термін, який ми раніше використовували для розрахунку потенційної енергії електрона в моделі Бора. Замість радіуса r ми використовуємо тепер квадратний корінь суми квадрата трьох координат x, y та z, щоб вказати кулонівську енергію електрона в будь-якому положенні всередині атома. Наша хвильова функція тепер буде функцією трьох координат x, y та z Це означає, що наша хвильова функція тепер буде тривимірною і представляти тривимірні стоячі хвилі. Тривимірні хвилі складніше уявити в порівнянні з 1-мірними, але мають ті ж властивості, які полягають в тому, що положення гребенів, западин, вузлів не рухається.
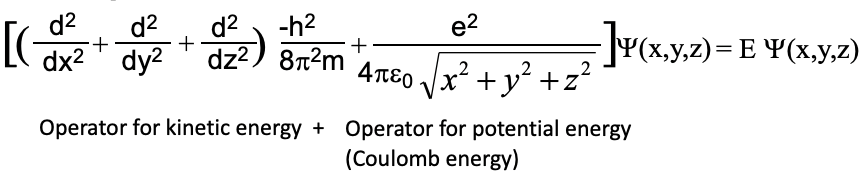
Рівняння 1.2.9 Рівняння Шредінгера для атома Н.
Щоб отримати хвильові функції для електрона, нам потрібно розв'язати рівняння Шредінгера для атома водню. Для цього нам потрібно подумати про граничні умови для хвильової функції. Однією з умов є те, що квадрат хвильової функції наближається до нуля, коли ми йдемо дуже далеко від ядра, а r, відстань від ядра наближається нескінченно. По-друге, як і в одновимірній коробці, інтеграл над квадратом хвильової функції повинен бути один. Це пояснюється тим, що ймовірність знайти електрон десь в атомі повинна бути 100%. По-третє, було б розумно припустити, що хвильова функція повинна бути безперервно диференційованою і однозначною (рис.1.2.13).

Сферична полярна система координат
Математичний процес для вирішення рівняння Шредінгера виходить за рамки цього курсу, і вас направляють на заняття з фізичної хімії та підручники для деталей. Ми лише наведемо короткий опис процесу тут. Математично простіше розв'язати рівняння Шредінгера в сферичних полярних координатах замість декартових координат. Тому отримано розв'язки рівняння Шредінгера, хвильових функцій, в полярних координатах. Положення точки задається трьома числами: радіальна відстань цієї точки від фіксованого початку, її полярний кут, виміряний від фіксованого зенітного напрямку, і азимутальний кут її ортогональної проекції на опорну площину, що проходить через початок і ортогональний зеніту, вимірюється від фіксованого орієнтирного напрямку на цій площині (рис.1.2.14).
Розв'язки рівняння Шредінгера
Тоді хвильова функція є функцією r, θ і φ, зокрема, це добуток радіальної хвильової функції, яка є функцією r, хвильовою функцією колатності, яка є функцією θ, і азимутальною хвильовою функцією, яка є функцією φ (Eq. 1.2.10). Побачити явні форми радіальних, колатитних і азимутальних функцій можна на рис.1.2.15.
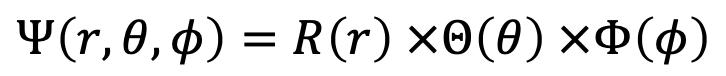
Рівняння 1.2.10 Хвильова функція для електрона в атомі Н як функція r, θ і φ
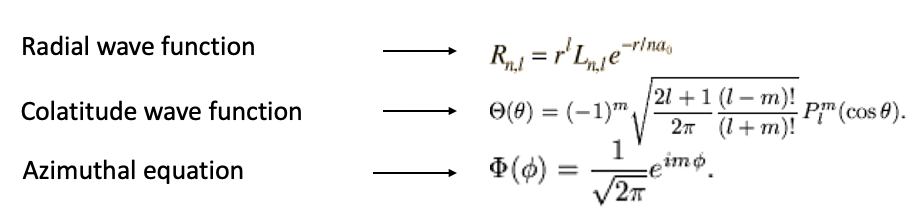
Тут нам не потрібно розбиратися у всіх подробицях, але потрібно усвідомити, що ці хвильові функції є функціями квантових чисел. На відміну від електрона в одновимірній коробці потрібно розглядати не тільки одне, а й три квантових числа. Поза квантовим числом n, яке називається основним квантовим числом, є також так зване орбітальне квантове число l та магнітне квантове число m Квантове число n зустрічається лише в радіальній хвильовій функції, квантове число l зустрічається лише в радіальній та широтній функції, а квантова число m зустрічається тільки в широті і азимутальної частини хвильової функції. Значення, які орбітальне квантове число l може прийняти, залежать від n, воно може бути між 0 і n-1 для даного квантового числа n. магнітне квантове число m залежить від квантового числа l, і може працювати від —l до+l. так, наприклад, коли n дорівнює 2, l може варіюватися між 0 і 1, а для l дорівнює 2, m може прийняти будь-яке значення між -2 і 2, а саме -2, -1, 0, +1 і +2 (рис.1.2.16).

Ці хвильові функції мають особливу назву в хімії. Їх називають орбіталями. Можна зрозуміти орбіту як тривимірну хвильову функцію, яка описує електрон в атомі як стоячу хвилю. Таким чином, орбіталь - це стан, який може прийняти електрон, і коли ми говоримо, що електрон знаходиться в певній орбіталі, ми маємо на увазі, що електрон знаходиться в певному стані.
Спінові квантові числа s
В межах орбіти електрон може приймати два різних спини, описані спіновим квантовим числом s Це квантове число не є результатом рівняння Шредінгера, але було знайдено експериментально. Спінові квантові числа s можуть приймати два значення: +1/2 і -1/2. Ми говоримо, що електрон обертається, коли s = +1/2, і обертається вниз, коли s = -1/2.
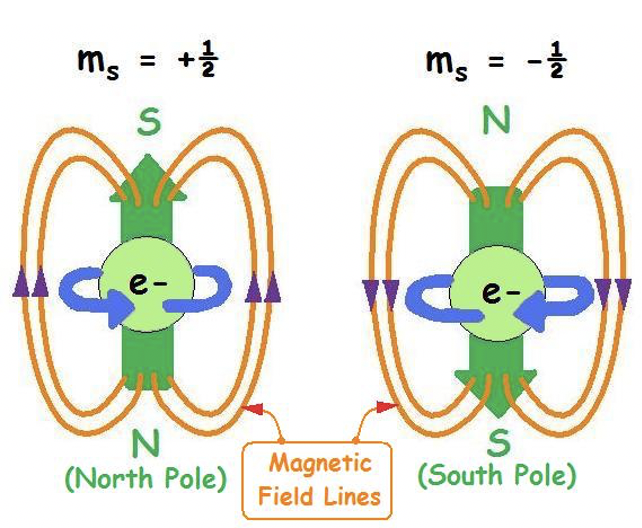
chem.libretexts.org/ @api /dek...jpg? перегляд = 1, CC BY-NC-SA 3.0)
Спінове квантове число зрозуміти найлегше, коли ви розглядаєте електрон як частинку, що обертається навколо власної осі. Обертання проти годинникової стрілки буде пов'язане з s = +1/2, обертання за годинниковою стрілкою буде пов'язане з s = -1/2. Обертання виробляє магнітне поле з напрямком ліній поля в залежності від напрямку обертання.
1-а орбітальна
Давайте тепер вставимо квантові числа в загальний вигляд хвильової функції для електрона в атомі водню і обчислимо їх явні математичні форми. Почнемо з найменших можливих чисел. Коли ми вставляємо n = 1, l = 0 і m = 0, ми отримуємо хвильову функцію для 1s орбіталі (Eq. 1.2.11).
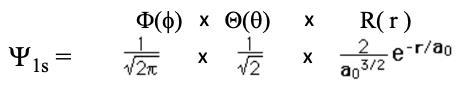
Рівняння 1.2.11 Хвильова функція для 1-ї орбіти
Ви можете бачити, що широтна та азимутальна частини хвильових функцій, разом також звані кутовою частиною хвильової функції, є простими числами, а саме одне над квадратним коренем двох пі, а одне над квадратним коренем двох відповідно. Кути тета і фі не з'являються, а це означає, що хвильова функція не залежить від кута. З цього випливає, що орбіталь має кулясту форму.

Радіальна частина хвильової функції має експоненціальний член e до потужності —r над a 0. Число e - число Ейлера, тобто основа натурального логарифма. Він приблизно дорівнює 2.71828. a 0 - радіус Бора, який є відстанню електрона від протона для електрона на його першій орбіті за моделлю атома Бора. Ми розрахували його раніше, і це було 5,29 х 10 -11 м. р - відстань від ядра. Цей експоненціальний термін має константу перед ним, яка дорівнює 1 над радіусом Бора до сили трьох над двома. Оскільки радіальна частина хвильової функції є e до потужності —r, амплітуда радіальної частини хвильової функції зменшується експоненціально зі збільшенням відстані r від ядра. Це вірно для всієї хвильової функції, оскільки кутові частини хвильової функції - це просто прості числа. Ви можете побачити експоненціальне зниження амплітуди хвильової функції як функції радіуса r в одиницях радіуса Бора a 0 на графіку нижче (рис.1.2.19).
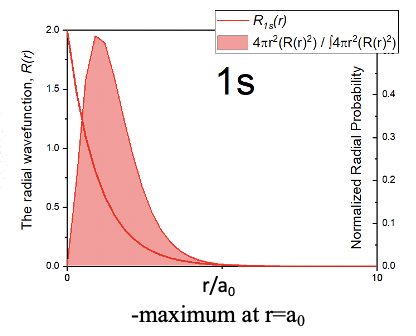
Це означає, що 1-я орбіта повинна бути сферичною орбітою з її амплітудою експоненціально зменшуватися зі збільшенням відстані від ядра. Це можна графічно зобразити через щільність точок навколо ядра (рис.1.2.18). Більш висока щільність точок означає більшу амплітуду, а менша щільність точок означає меншу амплітуду. Той факт, що амплітуда найбільш близька до ядра, означає, що ймовірність знайти електрон в тій чи іншій точці простору є найвищою найближчою до ядра. Це пов'язано з тим, що квадрат хвильової функції для 1s орбіталі представляє ймовірність знайти електрон в певній точці простору. Однак ймовірність знайти електрон на певній відстані від ядра не найвища найближча до ядра. Це пояснюється тим, що ймовірність знайти електрон на певній відстані від ядра - це ймовірність знайти електрон в певній точці простору на кількість точок у просторі, які мають таку конкретну відстань. Кількість точок у просторі, які мають певну відстань r від ядра, пов'язане з поверхнею сфери радіусом r Поверхня сфери A задається формулою A=4πR 2. Таким чином, ймовірність знайти електрон на певній відстані r від ядра дорівнює поверхні сфери з радіусом r, що перевищує квадрат радіальної хвильової функції. Це визначає функцію радіальної ймовірності R P =4πr 2 R 2.
Графік для функції радіальної ймовірності зображений на малюнку 1.2.19. Ви можете бачити, що це нуль, коли r = 0, який обумовлений терміном r 2, який стає нулем при r = 0. При малих значеннях r член 4πr 2 домінує над загальною функцією і ймовірність знайти електрон збільшується з r Однак, оскільки експоненціальний член радіальної функції стає все більш значним при більших значеннях r, функція радіальної ймовірності проходить через максимум, а потім знижується. На відстанях r наближаються нескінченні функція наближається до нуля Максимум кривої представляє відстань, на якому найімовірніше знайти електрон. Цікаво, що він дорівнює радіусу Бора r Це означає, що Бор все-таки не так помилявся. Однак він помилявся в тому сенсі, що розглядав електрон як класичну частинку, що знаходиться тільки в цьому радіусі. Натомість електрон, завдяки своїм хвильовим властивостям, знаходиться не тільки в радіусі Бора r 0, але, швидше за все, ми можемо знайти його там.
Результат того, що ймовірність знайти електрон в певній точці простору найбільша в ядрі, позбавить від питання про те, чому атом Н не руйнується. Оскільки амплітуда хвильової функції є найбільшою найближчою до ядра, ми можемо сказати таким чином, що атом згорнутий. Тим не менш, атом в основному порожній простір через делокалізацію хвильової функції, яка описує стан електрона. Делокалізація електрона завдяки своїм хвильовим властивостям також робить питання про розмір орбіти нетривіальним. Хвильова функція наближається до нуля лише для r наближається нескінченно, але ніколи не стає нулем. Це означає, що для обліку всієї електронної густини орбіталь була б нескінченно великою. Однак це не було б розумним визначенням. Загальновизнаним визначенням є те, що розмір орбіти визначається простором, який містить 90% його електронної щільності. Ми можемо зобразити орбіталі відповідно до цього визначення. Для випадку з орбіталлю 1s радіус сфери, яка представляє 1s орбіталь, вибирається так, що ймовірність знайти електрон у сфері цього радіуса становить 90%.
2-а орбітальна
Вставка n = 2, l = 0 і m = 0 в загальну хвильову функцію дає нам хвильову функцію для 2s орбіталі (Eq. 1.2.12).
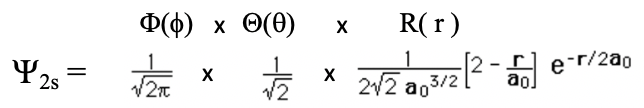
Рівняння 1.2.12 Хвильова функція для 2s орбіталі
Як і у випадку з орбіталлю 1s, кутові частини хвильової функції є лише простими числами. Таким чином, 2s орбіталь також є сферичною орбітою. Як і в 1-й орбіталі, радіальна частина хвильової функції має експоненціальний член типу e -r і простий коефіцієнт. Однак є додатковий термін 2-р/а 0. Через експоненціального члена амплітуда хвильової функції зменшується експоненціально з r Однак через термін 2-r/a 0 хвильова функція стає негативною, а потім наближається до 0. Радіус, при якому хвильова функція змінює свій алгебраїчний знак, називається сферичним вузлом. Вузол сферичний, оскільки він описує поверхню - це сфера. На поверхні цієї сфери амплітуда хвильової функції дорівнює нулю. Радіус, при якому хвильова функція змінює свій алгебраїчний знак, дорівнює 2a 0. Це стає зрозумілим, коли ми вважаємо, що термін 2-r/a 0 стає нулем, коли r = 2a 0, тому що 2-2a 0 /a 0 =0. Коли цей термін дорівнює нулю, то вся хвильова функція стає нулем. Ми можемо проілюструвати зміну алгебраїчного знака в орбіталі 2s за допомогою кольорів, як показано нижче (рис.1.2.20).
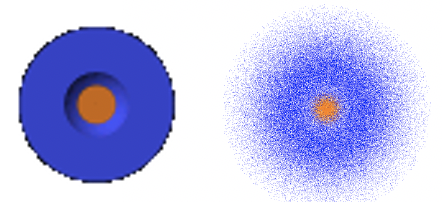
Помаранчева сфера вказує на простір, в якому амплітуда 2s орбіталі позитивна, а синя область вказує, де вона негативна. Область інтерфейсу, де змінюється колір, представляє вузол. Помноживши квадрат радіально-хвильової функції R на 4πr 2, отримаємо функцію радіальної ймовірності для 2s орбіти (рис.1.2.21).
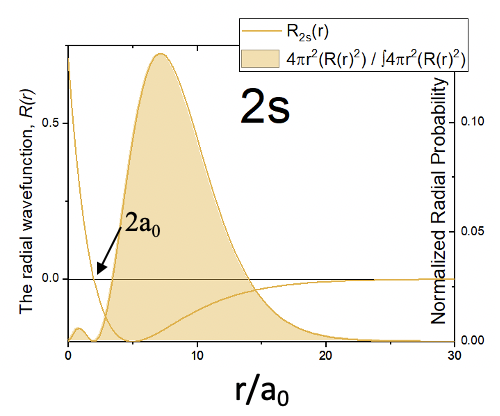
Ви можете бачити, що подібно до 1s орбіталі, ймовірність знайти електрон на радіусі, найближчому до ядра, дорівнює 0. Однак, на відміну від 1-ї орбіти, зараз є два максимуми замість одного. Цей другий максимум накладається сферичним вузлом 2s орбіталі. Другий максимум більше першого. Як правило, ймовірність знайти електрон далі від ядра більша порівняно з 1s орбіталлю. Це означає, що 2s орбітальний більше, ніж 1s орбітальний. Це відображає загальну тенденцію, що орбіталі з більшим квантовим числом n, як правило, більші, і ймовірність знайти електрон далі від ядра більша.
3-а орбітальна
Давайте подивимося на ще одну орбітальну, 3-ю орбітальну (ур. 1.2.13).
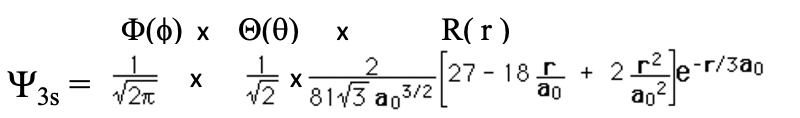
Рівняння 1.2.13 Хвильова функція для 3s орбіталі.
Кутові частини хвильової функції для 3s орбіталі знову є простими числами, що означає, що орбіталь знову сферична. Як правило, всі s орбіталі сферичні.
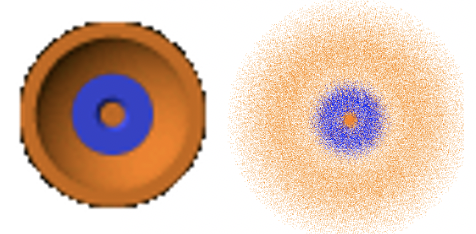
Радіальну частину хвильової функції можна розділити на частини. Перша частина - це просте число, далі йде термін 27-18r/a 0 + 2r 2 /a 0 2, і експоненціальний член e -r/3a 0. Через експоненціальної частини амплітуда хвильової функції зменшується експоненціально зі збільшенням r Однак тоді хвильова функція стає негативною, проходить мінімум, потім знову стає позитивною, проходить малий максимум і нарешті наближається до нуля. Той факт, що хвильова функція змінює свій алгебраїчний знак два рази, означає, що 3s орбіталь має два сферичних вузла. Ці сферичні вузли обумовлені другим терміном, який є квадратною функцією типу ax 2 + bx + c, за допомогою якого в даному випадку a = 2/a 0 2, b = -18/a 0 і c=27. Коли цей термін стає нулем, вся хвильова функція стає нулем. Квадратні функції мають два розв'язки за формулою x = (-b ± √ (b 2 -4ac)) /2a. Розчини дають радіуси для двох сферичних вузлів 3-ї орбіти. Ми опускаємо точний розрахунок радіусів для короткості та ясності причин тут. Ви можете обчислити їх як домашнє завдання.
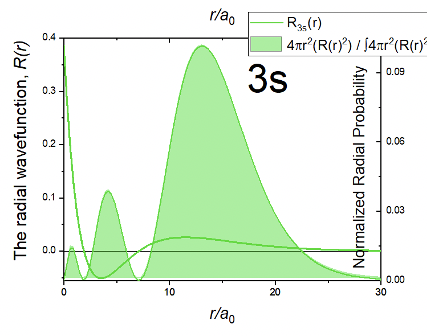
Через двох сферичних вузлів функція радіальної ймовірності R p має три максимуми. Дуже маленькі, близькі до ядра, більші на відстані від ядра, а найбільший - на ще більшій відстані від ядра. В цілому, 3s орбіталі більше, ніж 2s орбіталь підтверджує загальну тенденцію, що s орбіталі збільшуються в розмірах зі збільшенням квантового числа n.
2p z орбітальний
Тепер розглянемо орбіталі, в яких орбітальне квантове число l більше 0. Коли l дорівнює 1, то n має бути не менше 2. Орбітальна з n = 2 і l = 1 - це орбітальна 2p. Загалом, три орбіталі 2p повинні існувати, оскільки для l = 1 магнітне квантове число m може приймати три значення: -1, 0 та +1. Орбітальна з m = 0 називається орбітальною 2p z. Розглянемо математичну форму цієї хвильової функції (ур. 1.2.14).
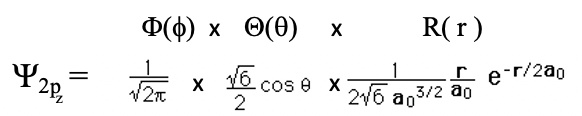
Рівняння 1.2.14 Хвильова функція для орбіталі 2p z
Аналіз кутових частин хвильової функції показує, що, хоча азимутальна частина все ще є простим числом, частина широти не є, це функція θ. Це означає, що амплітуда хвильової функції тепер залежить від кута, що означає, що орбіта не може бути сферичною. Замість цього орбітальна 2p має форму гантелі, яка орієнтована вздовж осі z. Одна частка знаходиться над площиною xy, а інша частка знаходиться нижче площини xy. Ці дві різні частки мають різний алгебраїчний знак, позначений різними кольорами (рис.1.2.24).
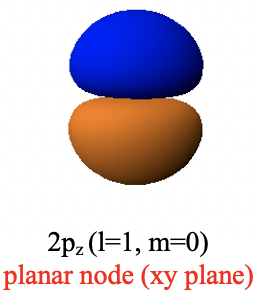
У межах площини xy амплітуда хвильової функції дорівнює нулю. Площина xy являє собою так званий плоский вузол. Площинний вузол - це різновид кутового вузла. Назва кутового вузла тому, що це пов'язано з тим, що кутова частина хвильової функції - це не просте число, а функція кута, в даному випадку θ. Ми можемо показати, що кутова частина хвильової функції створює плоский вузол у площині xy, коли ми перетворюємо його зі сферичних в декартові координати (ур. 1.2.15).
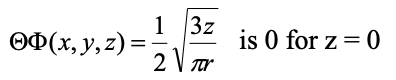
Рівняння 1.2.15 Кутова частина хвильової функції 2p z в декартових координатах. Функція стає нульовою, коли z=0.
Ми бачимо, що кутова частина хвильової функції є лише функцією z, ми також бачимо, що кутова частина хвильової функції стає нульовою, коли z=0. Коли кутова частина хвильової функції стає нульовою, то хвильова функція всієї орбіти стає нульовою. Z дорівнює нулю тільки в площині xy, і це пояснює, чому площина xy є планарним вузлом.
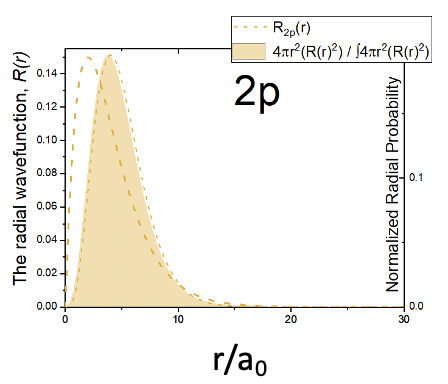
Тепер подивимося на радіальну частину хвильової функції. Він складається з трьох членів: простої константи, терміна r/a 0 і експоненціального члена e -r/2a 0. Через термін r/a 0 радіальна частина хвильової функції дорівнює нулю при r=0. Це означає, що дуже малоймовірно знайти електрон в точці простору безпосередньо біля ядра. Така поведінка протилежна s орбіталів. Оскільки термін r/a 0 домінує над поведінкою хвильової функції при малому значенні r, амплітуда спочатку збільшується. Однак при більших значеннях r експоненціальний член стає більш важливим, який змушує амплітуду радіальної функції через максимум, після чого вона знижується і наближається до нуля. Радіально-хвильова функція ніколи не змінює алгебраїчний знак. Тому орбітальна 2p z не має сферичного вузла. Радіальна функція ймовірності має аналогічну форму порівняно з радіальною функцією. Він дорівнює нулю при r=0 і проходить максимум, перш ніж знову знизиться і наблизиться до нуля (рис. 1.2.25).
2p x і 2p y орбітальний
Орбіталі 2p x та 2p y отримують, коли квантові числа m дорівнюють 1 та -1 відповідно.
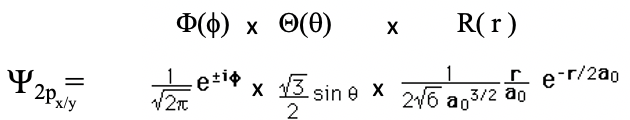
Рівняння 1.2.16 Хвильова функція для орбіталі 2p x та 2p y
Вони мають ту ж форму, що і орбітальні 2p z, але орієнтація у них різна. Гантель орбітальної 2p x орієнтована вздовж осі x, а орбітальна 2p y орієнтована вздовж осі y.
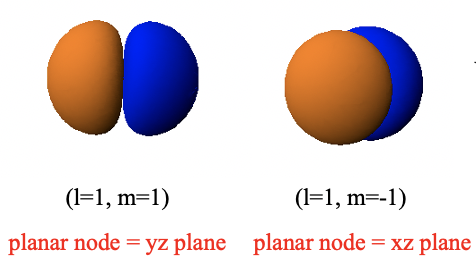
Це пов'язано з тим, що орбітальна 2p x має плоский вузол в площині yz, а орбітальна 2p y має плоский вузол в площині xz. Плоскі вузли обумовлені кутовою частиною хвильових функцій цих орбіталей.
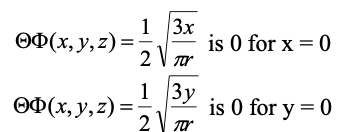
Рівняння 1.2.17 Кутова частина хвильової функції 2p x і 2p y відповідно. Хвильові функції стають 0 для x=0 та y=0 відповідно.
Як видно, кутові частини хвильової функції містять як кути θ, так і Φ. При перетворенні в декартові координати (Eq. 1.2.17) можна побачити, що кутова функція орбіталі 2p x є лише функцією x, а кутова функція 2p y орбіталі є лише функцією y. X дорівнює нулю тільки в площині yz, а y дорівнює нулю тільки в площині xz, отже, ці вузли є площинними вузлами. Радіальна хвильова функція точно така ж, як і для орбітальної 2p z.
Орбіталі 3p
Тепер давайте подивимося на орбіталі 3p. В орбіталі 3p квантове число n = 2 і l = 1. Як і у випадку з орбіталями 2p, є три орбіталі p, оскільки магнітне квантове число m може приймати значення -1, 0 та +1. Хвильова функція орбіти 3p z показана нижче (ур. 1.2.18).
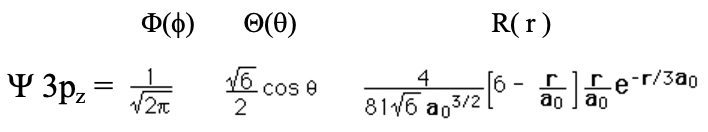
Рівняння 1.2.18 Хвильова функція для орбіталі 3p z
Можна помітити, що кутова частина хвильової функції точно така ж, як і для орбіталі 2p z. Це означає, що як і в орбіталі 2p z повинен бути плоский вузол в площині xy. Коли ви подивитеся на радіальну частину хвильової функції, ви можете побачити, що вона складається з чотирьох членів, простої константи, терміна 6-r/a 0, терміна r/a 0 та експоненціального члена e -r/3a 0. Через термін r/a 0 хвильова функція стає нульовою при r=0. Через термін 6-r/a 0 хвильова функція має сферичний вузол. Це тому, що коли 6-r/a 0 =0 вся хвильова функція стає 0. Ми можемо визначити радіус, при якому хвильова функція стає нульовою, вирішивши рівняння 6-r/a 0 =0 для r, що дає r=6a 0. Загалом радіальна функція дорівнює нулю при r=0, проходить максимум, змінює свій алгебраїчний знак на сферичному вузлі на r=6a 0, має мінімум, а потім наближається до нуля на дуже великих відстанях r (рис.1.2.28).
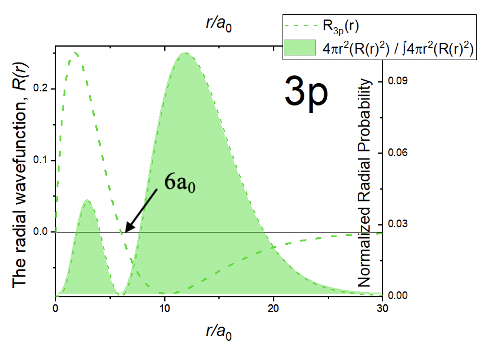
Функція радіальної ймовірності має два максимуми, малий близько до ядра, і більший далі від ядра. Загалом функція радіальної ймовірності знаходиться далі від ядра порівняно з орбіталями 2p, що означає, що орбіталь 3p більша.
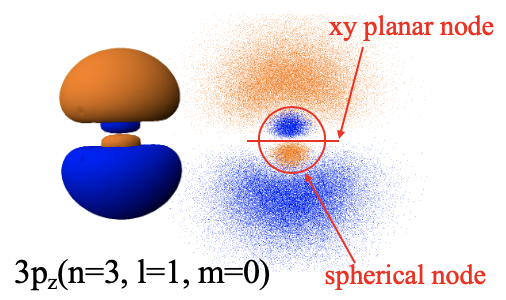
Загальна форма орбіталі 3p z визначається як сферичним, так і площинним вузлом (рис.1.2.29). Завдяки плоскому вузлу в площині xy він має форму гантелі і орієнтований в напрямку z. Однак через сферичного вузла алгебраїчний знак хвильової функції змінюється в межах двох часток гантелі. Нарешті, давайте розглянемо 3p x і 3p y орбіталі. Вони мали б таку ж форму, як орбітальна 3p z, але вони були б орієнтовані відповідно у напрямку x та y. Ми також могли б подумати про те, що станеться з орбіталями p, якщо ми збільшимо квантове число n далі. В цьому випадку форма гантелей залишилася б, але були б введені додаткові сферичні вузли. Орбітальна 4p мала б два сферичні вузли, 5p орбітальні три сферичні вузли тощо. Розмір цих p орбіталів також збільшувався б з квантовим числом n.
3d z 2 орбітальний
Тепер розглянемо орбіталі з орбітальним квантовим числом l=2. Ці орбіталі є так званими d-орбіталями. Оскільки основне квантове число n завжди має бути принаймні на одне ціле число більше квантового l, орбіталі d з найменшим квантовим числом n є 3d орбіталями. Для кожного квантового числа n має бути п'ять d орбіталей, оскільки для l = 2 магнітне квантове число m може приймати значення -2, -1, 0, -1, +1 та +2. Давайте спочатку подивимося на 3d орбіталі з m = 0. Ця орбітальна називається 3d z 2 орбітальною. Його хвильова функція показана нижче (ур. 1.2.19).
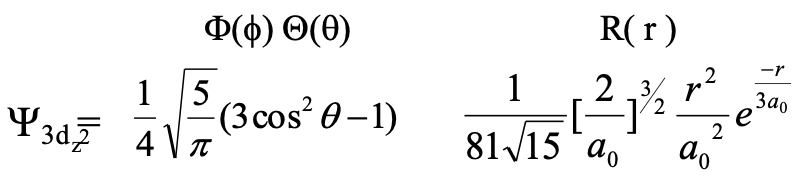
Рівняння 1.2.19 Хвильова функція для 3d орбіталі z 2
Ви можете бачити, що радіальна функція є добутком трьох членів: константи, члена r 2 /a 0 2 та експоненціального члена e -r/3a 0. Експоненціальний термін такий же, як і для орбіталей 3p. Через термін r 2 /a 0 2 амплітуда хвильової функції дорівнює 0 при r=0. Амплітуда потім збільшується з r, проходить максимум, а потім наближається до нуля. Це означає, що хвильова функція ніколи не змінює свого алгебраїчного знака, а тому не має сферичних вузлів. Функція радіальної ймовірності має аналогічну форму в порівнянні з радіальною функцією (рис. 1.2.30). Імовірність електронів дещо далі від ядра порівняно з орбіталями 3p, що означає, що 3d орбіталь дещо більша, ніж орбіталь 3p.
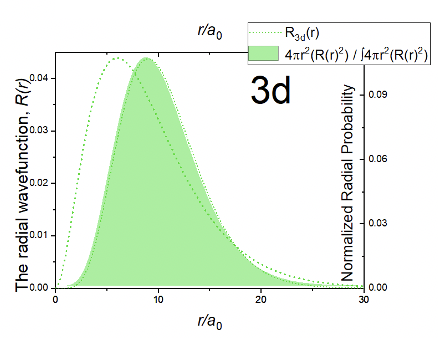
Ви можете бачити, що кутова частина хвильової функції є функцією θ, що означає, що орбіталь буде несферичною і буде принаймні один кутовий вузол. При цьому кутові вузли представляють собою два конічних вузла. Ці вузли описують два конуса, які надають орбіталі характерну форму. Це пончикове кільце в площині xy навколо гантелі, що вказує в напрямку z. Гантель і пончик мають різні алгебраїчні знаки, позначені різними кольорами (рис. 1.2.31). Зверніть увагу, що на відміну від p орбіталів дві частки гантелі мають однаковий алгебраїчний знак.
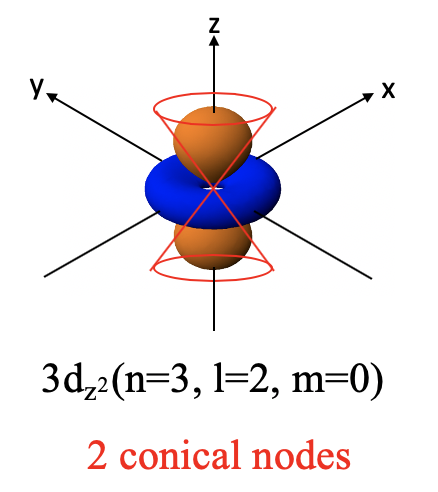
Ми можемо зрозуміти, що 3d z 2 орбіталь має два конічних вузла, коли ми перетворюємо кутову частину хвильової функції в декартові координати (ур. 1.2.20).
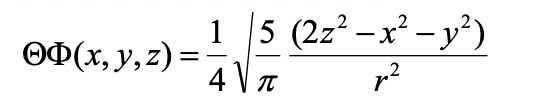
Рівняння 1.2.20 Кутова частина хвильової функції 3d z 2 орбіталі в декартових координатах.
Ви можете бачити, що це функція 2z 2 -x 2 -y 2. Це математична форма конусів. Кутова частина хвильової функції стає 0, коли 2z 2 = x 2 -y 2, що вірно на поверхні двох конусів, один над площиною xy і один нижче площини xy. Назва 3d z 2 орбітальна тому, що це функція z 2.
3d х 2 -y 2 орбітальний
Давайте далі подивимося на 3d x 2 -y 2 орбіталі (ур. 1.2.21).
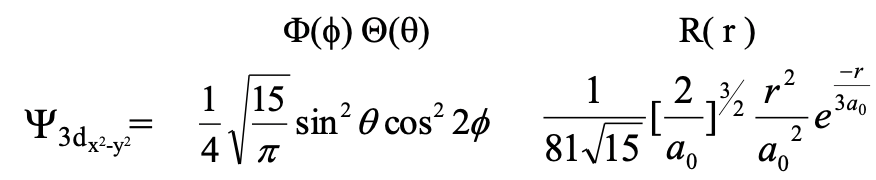
Рівняння 1.2.21 Хвильова функція для 3d x 2 -y 2 орбіталі
Радіальна частина хвильової функції така ж, як і для 3d z 2 орбіталі. Кутова частина хвильової функції є одночасно функцією θ і Φ, і, таким чином, є кутові вузли, які слід очікувати. Ми можемо знайти їх знову, коли ми перетворимо кутову частину хвильової функції зі сферичних в декартові координати.
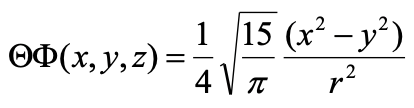
Рівняння 1.2.22 Кутова частина хвильової функції 3d x 2 -y 2 орбіталі в декартових координатах.
Ви можете бачити, що кутова функція є функцією x 2 -y 2. Функція стає нульовою, коли x 2 -y 2 =0. Це той випадок, коли x=y або x = -y. X дорівнює y на двох лініях, які розділяють кут 90 градусів між віссю x і y. Координата z повністю змінна. Таким чином, загалом хвильова функція стає нульовою на двох площинях, які стоять перпендикулярно площині xy і бісекція кута 90 градусів між осі x і y. Таким чином, ці дві площини є двома площинними вузлами орбіти.
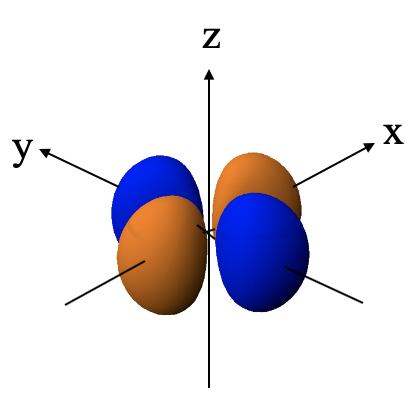
Через двох плоских вузлів орбітальна має чотири частки, що лежать на осі x і y відповідно. Частки, що лежать на осі х, мають протилежний алгебраїчний знак в порівнянні з тими, що лежать на осі у. Назва орбітальної dx 2 -y 2 полягає в тому, що це функція x 2 -y 2.
3d xy, 3d yz і 3d xz орбіталі
Решта d орбіталів - це 3d yz, 3d xz та 3d xy. Радіальна функція цих орбіталів подібна до тих, які ми обговорювали раніше. Кутова частина хвильових функцій показана тут безпосередньо в декартових координатах. Орбітальна d yz є функцією yz. Функція стає нульовою, коли y=0 або z=0. y дорівнює нулю в площині xz, а z дорівнює нулю в площині xy. Тому ці площини є площинними вузлами орбіти. Через ці вузли орбітальна має чотири частки, які лежать у площині yz, завдяки чому частки знаходяться між осями y та z. Зверніть увагу, що сусідні частки мають протилежний алгебраїчний знак, а протилежні частки мають однаковий алгебраїчний знак.
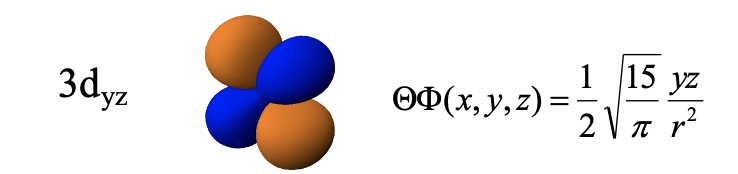
Орбітальна 3d xz є функцією xz, і, таким чином, функція стає нульовою з x = 0 або z=0. Це визначає, що yz та xy площини як два плоских вузли. Орбітальна має таку ж форму, як і 3d yz, за винятком того, що чотири частки лежать в площині xz замість площини yz.
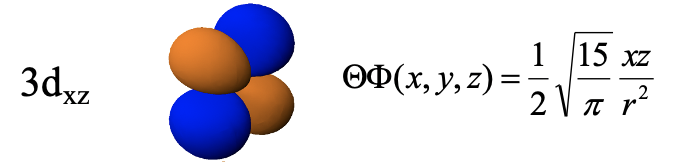
3d xy -орбітальна є функцією xy, і, таким чином, його хвильова функція стає нулем при x = 0 або y = 0. Тому площини xz та yz є площинними вузлами, а орбітальна має чотири частки в площині xy між віссю x та y. Зверніть увагу, що 3d xy та 3d x 2 -y 2 виглядають дуже схожими, але відрізняються. Різниця полягає в тому, що орбітальна 3d x 2 -y 2 має свої частки на осі x та y, тоді як 3d xy орбіталі має частки між осями x та y. Можна також сказати, що 3d x 2 -y 2 орбіталь обертається на 45 градусів навколо z по відношенню до 3d xy орбіталі.
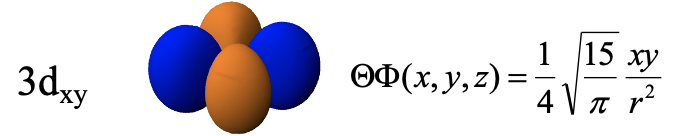
Правила для кутових і сферичних вузлів
Звичайно, тепер ми могли б обговорити розмір і форму багатьох інших орбіталів, таких як 4d орбіталі або орбіталі 4f, але це буде поза сферою дії. Замість цього давайте подумаємо, чи існують загальні правила, які дозволяють передбачити кількість сферичних і кутових вузлів в орбіталі. Кількість радіальних вузлів завжди дорівнює n-l-1, кількість кутових вузлів дорівнює l, а загальна кількість вузлів завжди n-1. Це означає, що кількість вузлів збільшується з квантовим числом n Якщо збільшити квантове число l для заданого квантового числа n, то ми замінюємо сферичні вузли кутовими. Це підсумовано на малюнку 1.2.36.

Орбітальні енергії для атома H
Рівняння Шредінгера дозволяє не тільки обчислити орбіталі атома водню, але і їх енергії. Енергії моделі Бора і Шредінгера збігаються: E = константа/n 2: Це означає, що орбіталі з однаковим квантовим числом n мають однакові енергії. Енергії не є функцією квантових чисел l і m. Енергії негативні, оскільки вони є зв'язуючими енергіями. Іншими словами: Додавання електрона до протона - це екзотермічний процес. Енергія зв'язку для енергії збільшується в міру зменшення енергії орбіти (рис.1.2.37).
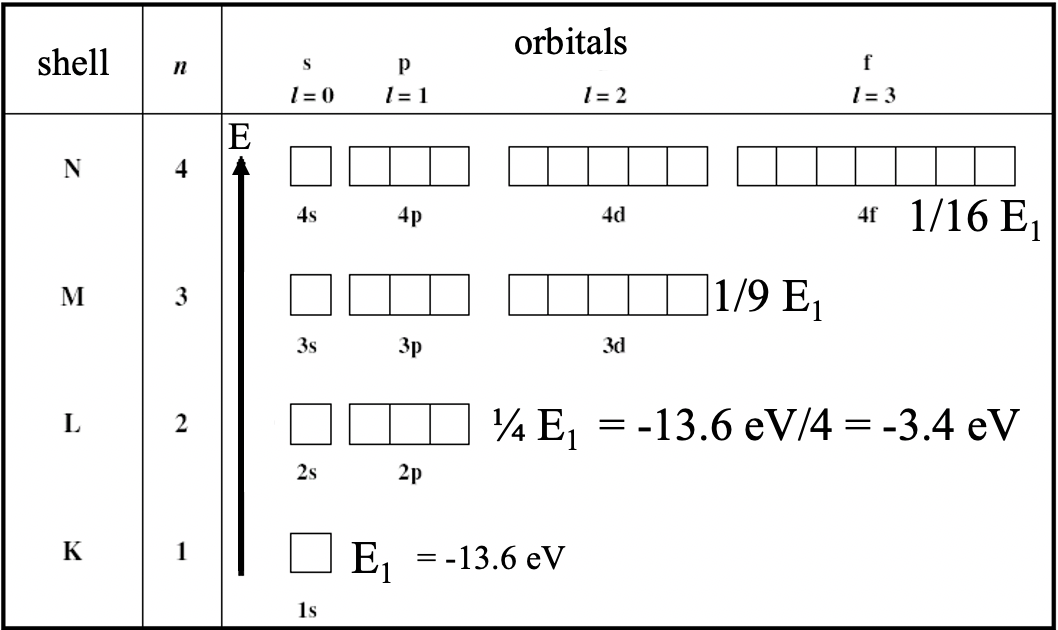
Для 1s орбіталі H енергія -13.6 еВ, енергія 2s і 2p орбіталів ¼ цього, енергія 3s, 3p і 3d орбіталів становить 1/9 енергії 1s орбіталі і так далі. Примітка при ¼ і 1/9 від -13.6 еВ більше -13,6 еВ через негативний алгебраїчний знак. Електронвольт - одиниця енергії. Це кількість кінетичної енергії, отриманої одним незв'язаним електроном, коли він проходить через електростатичну різницю потенціалів в один вольт, у вакуумі.
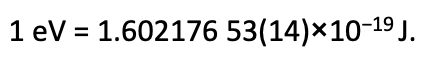
Рівняння 1.2.23 Перетворення електронвольт в джоуль одиниці.
Іншими словами, він дорівнює одному вольту (1 вольт = 1 джоуль на кулон) раз заряду одного електрона (в кулоні). Це дуже мала одиниця енергії, яка практична для розрахунків орбітальної енергії, оскільки орбітальні енергії дуже малі (екв. 1.2.23).
Багатоелектронні атоми
Поки що ми розглядали лише орбіталі атома водню, який містить лише один електрон. Чи можемо ми також вирішити рівняння Шредінгера для атомів, які мають більше одного електрона, і отримати точні енергії орбіталів? Відповідь - ні, це математично неможливо. Процес просто вже занадто складний навіть для всього двох електронів. Рівняння Шредінгера може бути розв'язано лише для однієї електронної системи. Тому опис атомної структури всіх інших атомів має працювати з наближеннями. Розглянемо спочатку атом Він. У ньому всього на один електрон більше, ніж водню. Це корисний підхід до наближення багатоелектронних атомів спочатку як одноелектронних систем, а потім наближення електрон-електронних взаємодій. Енергії електронів в атомі з більш ніж одним протоном повинні слідувати рівнянню E n =-Z 2 x13,6 Ev/n 2, в якому Z - число протонів.
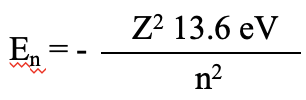
Рівняння 1.2.24 Орбітальні енергії для атомів з більш ніж одним протоном
Енергія зв'язку електрона збільшується пропорційно квадрату числа протонів, оскільки привабливі кулонові сили, що діють на негативно заряджені електрони, збільшуються з кількістю позитивно заряджених протонів в ядрі. Можна експериментально виміряти орбітальні енергії за допомогою енергій іонізації. Енергія, необхідна для видалення електрона в певній орбіталі з атома, дорівнює енергії зв'язку для електрона в цій орбіталі. Тому енергія іонізації IE = -E n (E n = орбітальна енергія). Згідно з моделлю Шредінгера орбітальна енергія гелієвого електрона в 1s орбіталі повинна бути E 1s =- (2 2 × 13,6 еВ) /1 1 =-54,4 еВ (Eq. 1.2.25).
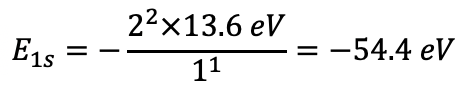
Рівняння 1.2.25 Енергія гелієвого електрона в 1s орбіталі.
Однак експериментально виміряна енергія іонізації електрона становить +24,6 еВ, що означає, що реальна орбітальна енергія дорівнює -24,6 еВ, а не -54,4 еВ. З іншого боку, іонізація іона He + становить +54.4 еВ, що саме те, що ми очікуємо. Ми можемо пояснити це явище тим, що модель Шредінгера працює лише для одного електрона і повинна нехтувати електронними взаємодіями. У іоні He + є тільки один електрон, тому модель Шредінгера правильно прогнозує енергію електрона. Однак в атомі гелію є два електрони, і модель Шредінгера не може враховувати електрон-електронні взаємодії. Тому він не дає правильної енергії для електронів в атомі гелію. Електронно-електронні взаємодії можна розглядати як екрануючі ефекти. Це означає, що перший електрон екранує частину ядерного заряду від другого електрона. Тому другий електрон відчуває знижену кулонівську силу від ядра. Через зниженої кулонівською сили енергія зв'язування менше. Знижується з -54,4 еВ до -24,6 еВ. Слід зазначити, що два електрони в 1s орбіталі атома Він не відрізняються, це означає, що вони обидва мають знижену енергію зв'язку. Енергія зв'язку збільшується лише до -54,4 еВ після видалення одного з двох електронів.
Чистий позитивний заряд від ядра після обліку екрануючих ефектів називається ефективним ядерним зарядом. Для атома гелію ефективний ядерний заряд становить 1,34. Розрахувати ефективний ядерний заряд можна з експериментально виміряної першої енергії іонізації. Розв'язування рівняння для Z eff дає Z eff =1.34 (ур. 1.2.26).
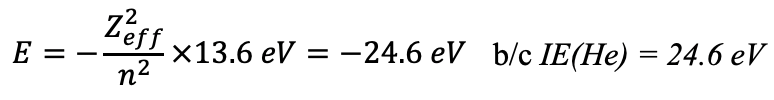
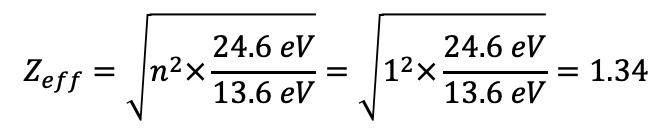
Рівняння 1.2.26 Розрахунок Z eff в атомі гелію від перших енергій іонізації.
Атом літію
Тепер перейдемо до атома з трьома електронами, атома літію. Дотримуючись так званого принципу Ауфбау, ми б заповнили перші два електрони в 1s орбіталі, оскільки 1s орбіталь є орбіталлю з найменшою енергією. Однак третій електрон не вписується в 1s орбіталь через принцип Паулі.

Принцип Паулі стверджує, що жоден два електрони в атомі не може мати однакових чотирьох квантових чисел. З цієї причини орбітальна не може вмістити більше двох електронів. У межах орбіти два електрони повинні мати різні спінові квантові числа s. Ми можемо вказати це, записуючи електрони у вигляді стрілок, спрямованих вгору і вниз, в квадратну коробку, яка представляє орбіталь. Третій електрон літію повинен був би перейти на орбіту з наступною вищою енергією.

Згідно з моделлю Шредінгера, енергія орбіти є лише функцією квантового числа n, і у нас буде два варіанти: орбіталі 2s та 2p. Обидва вони мали б однакову енергію. Однак в атомі літію 2s орбіталь має дещо нижчу енергію, ніж орбітальна 2p. Це знову можна пояснити екрануючими ефектами. 2s орбіталь проникає в 1s орбіталі трохи краще, ніж 2p орбіталі. Через це 1s орбіталі екранує ядерний заряд від ядра менше для 2s орбіталі порівняно з 2p орбіталями. Отже, електронна конфігурація наземного стану, яка є конфігурацією атомних електронів, що має найменшу енергію, повинна бути 1s 2 2s 1. Ми бачимо, що орбіталь 2s проникає в орбіталь 1s трохи краще, ніж орбіталь 2p з графіка для радіальних функцій ймовірності орбіталів, показаних на малюнку 1.2.40.
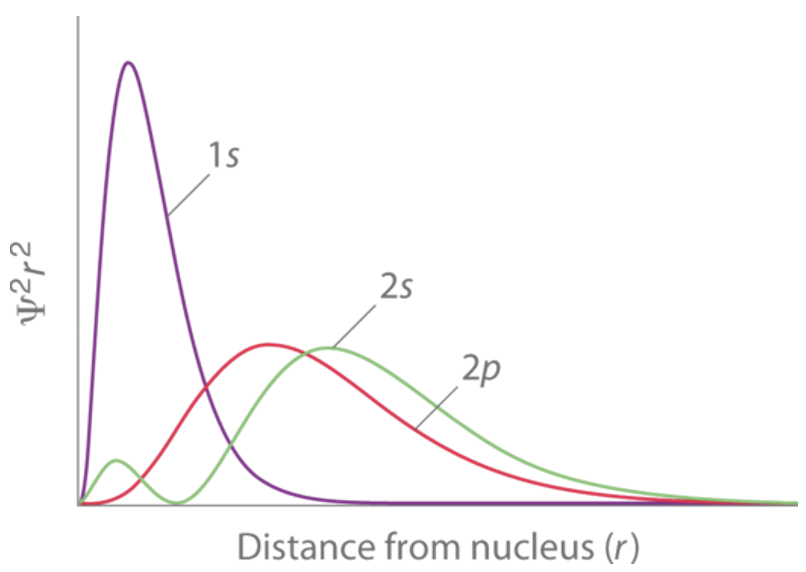
Другий великий максимум функції 2s орбіталі насправді далі від ядра порівняно з максимумом, пов'язаним з орбітальною 2p. Однак, оскільки 2s орбіталь має невеликий другий максимум дуже близько до ядра, 2s орбітальний загалом проникає в 1s орбіталь краще, і тому екрануючий ефект 1s орбіталі на 2s орбіталі менший порівняно з 2p орбіталями.
Взагалі можна сказати, що чим менше квантове число l для даного квантового числа n, тим краща здатність проникнення цієї орбіти. Завдяки кращій здатності проникнення екранування менше і, таким чином, ефективний ядерний заряд, який діє на електрон в орбіталі, вище. Більш ефективний ядерний заряд призводить до меншої енергії цієї орбіти. З цієї причини енергетична послідовність орбіталей з однаковим квантовим числом n збільшується від s до p до d до f.
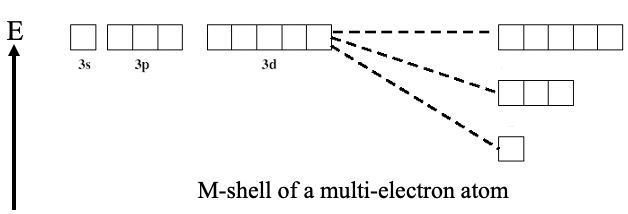
Наприклад, орбітальна 3s має меншу енергію, ніж орбітальна 3p, яка має меншу енергію, ніж 3d орбітальна (рис. 1.2.41).
Правила Слейтера
Оскільки орбітальну енергію можна обчислити з ефективного ядерного заряду, було б корисно, якби ефективний ядерний заряд можна було якось оцінити простими наближеннями.

Так звані правила Слейтера, названі на честь їх розробника Джона Слейтера (рис. 1.2.42), є простим інструментом, що дає хорошу оцінку ефективного ядерного заряду орбіталей в багатоелектронних атомах. Правила Слейтера оцінюють захисну константу σ, що дозволяє обчислити ефективний ядерний заряд Z eff від ядерного заряду за Z eff =Z-σ.
Правила оцінки σ наступні. По-перше, потрібно визнати, що правила для s і p електронів трохи відрізняються від правил для d і f електронів. Це пояснюється тим, що s і p електрони одного квантового числа n мають дещо вищу здатність проникнення в порівнянні з d і f електронами. Для обох груп перший крок однаковий. Виписуємо електронну конфігурацію атома за їх квантовими числами n і l, як показано нижче (рис.1.2.43).

Врахуйте, що цей порядок точно не відображає порядок енергій. Електрони, які мають схожі екрануючі ефекти, згруповані разом в дужки. Ви можете бачити, що s і p орбіталі одного квантового числа n будують групу, всі інші орбіталі є власною групою.
Щоб оцінити константу екранування для орбітальної s або a p, тепер ми можемо застосувати наступні правила:
а) Електрони праворуч від групи (ns, np) нічого не сприяють σ. Це тому, що ці електрони знаходяться далі від ядра, ніж електрон розгляду.
б) Кожен з інших електронів в тій же (ns, np) групі вносять від 0,35 до σ. Ці електрони знаходяться в тій же оболонці, що і електрон розгляду, і, таким чином, мають аналогічну відстань до ядра. З цієї причини їх екранування лише скромне і може бути оцінено приблизно в 35% від повного елементарного заряду, або 0,35.
в) Кожен електрон в оболонці n-1 вносить від 0,85 до σ. Ці електрони значно ближче до ядра порівняно з електроном розгляду. З цієї причини вони захищають значно краще, приблизно 85% елементарного заряду, або 0,85.
г) Кожен електрон в оболонці n-2 або нижче вносить від 1,00 до σ. Ці електрони набагато ближче до ядра, ніж електрон розгляду і можуть повністю екранувати елементарний заряд. Тому його внесок у екрануючу константу наближено до 1.
Тепер давайте розглянемо правила Слейтера для d і f електронів.
а) Електрони праворуч від (nd) або (nf) групи нічого не сприяють σ. Це знову тому, що електрон знаходиться далі від ядра, ніж електрон розгляду, і, таким чином, не може сприяти екрануванню.
б) Кожен з інших електронів в тій же (nd) або (nf) групі вносять від 0,35 до σ. Це знову тому, що ці електрони мають аналогічну відстань порівняно з електроном, для якого ми обчислюємо захисну константу, і, таким чином, екранування скромне.
в) Кожен електрон зліва від (nd) або (nf) групи вносить від 1 до σ. Ці електрони вважаються набагато ближче до ядра, і таким чином вони захищають повний елементарний заряд.
Зверніть увагу, що значення 0,35, 0,85 і 1 були обрані таким чином, щоб результати з правил Слейтера були в найкращій відповідності з експериментальними вимірами орбітальних енергій. Пам'ятайте, коли ми обговорювали атом гелію, ми говорили, що вимірювання енергій іонізації може забезпечити експериментальні орбітальні енергії.
Правила Слейтера, що застосовуються до багатоелектронних атомів
Давайте практикуємо правила Слейтера на кількох прикладах. Ми можемо, наприклад, обчислити ефективний ядерний заряд, який діє на електрон 2p в атомі кисню. Щоб відповісти на це питання, нам потрібно спочатку записати електронну конфігурацію відповідно до квантових чисел n і l і правильно згрупувати орбіталі (рис.1.2.44).
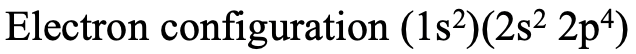
Далі потрібно врахувати, що ефективний ядерний заряд Z eff - це ядерний заряд Z мінус захисна константа σ. Тоді, оскільки кисень має вісім протонів, ядерний заряд дорівнює 8. З цього нам потрібно відняти екрануючу константу. По-перше, ми повинні усвідомити, що є 5 електронів в тій же групі, що і 2p електрон розгляду. Це два електрони 2s і три інших 2p електрони. Ці п'ять електронів екранують з коефіцієнтом 0,35, оскільки вони знаходяться в тій же групі, що і електрон 2p, для якого ми хочемо обчислити константу екранування. Зауважте, що цей четвертий 2p електрон не отримує коефіцієнта, оскільки це електрон, для якого ми обчислюємо константу екранування. Крім того, нам потрібно розглянути два електрона 1s. Вони знаходяться в n-1 оболонці, тому сприяють з коефіцієнтом 0,85. В цілому ефективний ядерний заряд на електроні 2р дорівнює 8- (2 х 0,85) - (5 х 0,35) = 4,55 (рис.1.2.45).
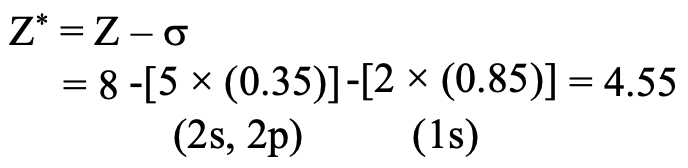
Ми також можемо запитати, що таке ефективний ядерний заряд на електроні 1s в атомі кисню. Вона становить 8-0,35=7,65 (рис.1.2.46).
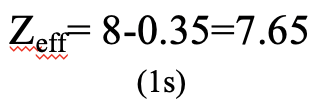
Це тому, що нам потрібно лише розглянути другий електрон на орбіталі 1s, щоб обчислити константу екранування σ. Він сприяє коефіцієнту 0,35, оскільки він знаходиться в тій же групі, що і 1-й електрон розгляду. Електрони 2s та 2p знаходяться в групі прямо до орбіталі 1s, тому вони не сприяють екрануванню.
Правила Слейтера та принцип Ауфбау
Правила Слейтера дуже допомагають зрозуміти так званий принцип Ауфбау, який говорить про те, що для атома в основному стані електрони знаходяться на орбіталі найнижчої енергії. В якійсь мірі енергії орбіталів слідують за квантовим числом n, але це не завжди так. Наприклад, елемент калій має електронну конфігурацію 1s 2 2s 2 2p 6 3s 2 3p 6 3p 6 3p 6 3d 0 4s 1 а не 1s 2 2s 2 2p 6 3s 2 3p 6 3p 6 3d 1. Це означає, що енергія 3d орбіталі повинна бути вище, ніж енергія орбіталі 4s. Чи можуть правила Слейтера передбачити це? Тому обчислимо енергію 3d і 4s орбіталі, використовуючи правила Слейтера, і подивимося, чи виходить енергія 3d орбіталі вище, ніж електрон 4s орбіталі.
Для 3d орбітальної константа екранування становить 18x1 = 18, оскільки крім 3-го електрона розгляду є 18 електронів, і всі 18 електронів знаходяться в нижній оболонці. Тому всі вони сприяють з коефіцієнтом 1. Ядерний заряд Z калію дорівнює 19. Тому ефективний ядерний заряд Z eff = 19-18=1 (рис.1.2.47).

Тепер зробимо аналогічний розрахунок для електрона 4s. Для 4-х електронів застосовуються правила Слейтера для s електронів. Відповідно до цього, два 3s та шість електронів 3p сприяють 0,85 до екрануючої константи, оскільки вони знаходяться в оболонці n-1. Решта два 1s, два 2s і шість 2p електронів знаходяться в n-2 або нижній оболонці і тому сприяють з коефіцієнтом 1. Тому загальна константа екранування становить 8 х 0,85 + 10 х 1 = 16,8. Отже, ефективний ядерний заряд Z eff становить 19-16,8 = 2,2 (рис. 1.2.48).
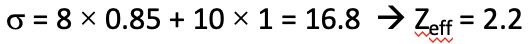
Ми бачимо, що більш ефективний ядерний заряд діє на електрон 4s порівняно з 3d електроном, що вказує на те, що орбітальна енергія для електрона 4s буде нижчою в порівнянні з 3d електроном. Ми можемо обчислити орбітальні енергії за формулою E= (Z eff 2) /n 2 × 13,6 еВ (ур. 1.2.27).
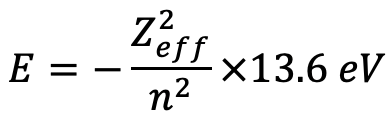
Рівняння 1.2.27 Рівняння для орбітальних енергій
Для 3d електрона вставляємо Z eff =1 і n = 3, що дає -1,51 еВ, екв. 1.2.28.
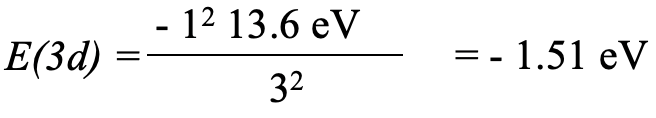
Рівняння 1.2.28 Рівняння орбітальної енергії 3-го електрона калію
Для 4s електронної вставки Z eff = 2.2 і n = 4, що дає -4,14 еВ.

Рівняння 1.2.29 Рівняння орбітальної енергії 4-х електрона калію
Як і очікувалося, енергія 4s електрона нижче енергії 3d електрона. Це пояснює, чому електронна конфігурація з електроном 4s як валентним електроном є кращою, ніж з 3d електроном як валентним електроном. Загалом, ми бачимо, що правила Слейтера можуть правильно передбачати електронні конфігурації атомів та принцип Ауфбау.
Давайте зробимо ще один, більш складний приклад: Для Fe існує дві мислимі конфігурації електронів. Один, в якому підоболонка 4s заповнюється перед 3d підоболонкою, і той, в якому 3d підоболонка заповнюється перед підоболонкою 4s. Для першого випадку електронна конфігурація 1s 2 2s 2 2p 6 3s 2 3s 2 3p 6 4s 2 3d 6. Для другого випадку друга конфігурація електронів - 1s 2 2s 2 2p 6 3s 2 3s 2 3p 6 3d 8 4s 0. Ми бачимо, що дві електронні конфігурації однакові для електронів 1s, 2s, 2p, 3s та 3p. Тому ми орієнтуємося на решту восьми електронів, позначені червоним кольором, і обчислюємо їх енергії.
У цьому випадку нам потрібно порівняти суму енергій електронів для обох електронних конфігурацій, щоб мати можливість вирішити, яка електронна конфігурація є сприятливою. Обчислимо суму енергій восьми електронів для першої електронної конфігурації наступним чином: На першому кроці нам потрібно переписати електронну конфігурацію у вигляді Слейтера: (1s 2) (2s 2 2p 6) (3s 2) (3s 2, 3p 6) (3s 2, 3p 6) (3d 6) (4s 2).
Далі ми можемо обчислити константу екранування для 3d електрона. Ми можемо ігнорувати два електрони 4s, оскільки вони знаходяться праворуч від d електрона розгляду, і не сприяють екрануванню. Однак нам потрібно розглянути п'ять інших 3d електронів, які знаходяться в тій же групі, що і 3d електрон розгляду. Вносять вони з коефіцієнтом 0,35. Інші 18 електронів сприяють 1,00, оскільки вони знаходяться в нижній оболонці. Оскільки ефективний ядерний заряд Fe дорівнює 26, ефективний ядерний заряд Z eff дорівнює Z eff = 26-19,75 = 6,25 (Eq. 1.2.30).
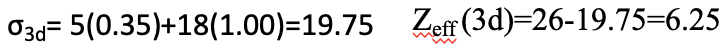
Рівняння 1.2.30 Рівняння для захисного постійного та ефективного ядерного заряду 3d електрона атома заліза
Для електрона 4s є ще один електрон 4s в тій же групі, що сприяє з коефіцієнтом 0,35. Крім того, в оболонці n-1 є 14 електронів, а саме 3s, 3p та 3d електронів. Вони сприяють 0,85 до константи екранування. Решта 10 електронів знаходяться в n-2 оболонці або нижче, тому сприяють з коефіцієнтом 1,00. Це дає загальну константу екранування 22,25. З цього ми можемо обчислити ефективний ядерний заряд для 4s електрона, який становить 26-22,25 = 3,75.
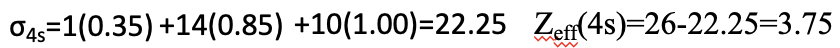
Рівняння 1.2.31 Рівняння для екранування постійного та ефективного ядерного заряду 4-х електронів атома Fe
Тепер ми можемо обчислити енергії електронів. Це сума енергій для 3d і 4s електронів. Енергія електронів для одного електрона E=- (Z eff 2) /n 2 ×13,6 еВ= - (6,25 2) /3 2 ×13,6 ЕВ = -59.03 еВ. Оскільки ми маємо шість 3d електронів, загальна енергія для шести електронів становить 6 х -59.03 еВ = -354,17 еВ (екв. 1.2.32).
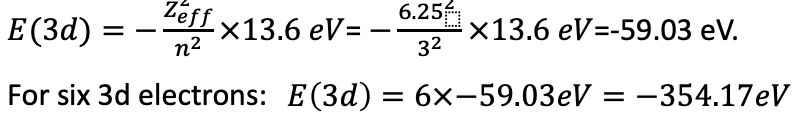
Рівняння 1.2.32 Рівняння енергій електронів шести 3d електронів в атомі заліза
Енергія одного електрона 4s дорівнює Е=- (3,75 2) /4 2 × 13,6 еВ = -11,95 еВ. Для двох 4s електронів енергія становить 2 х -11,95 еВ = -23,90 еВ.
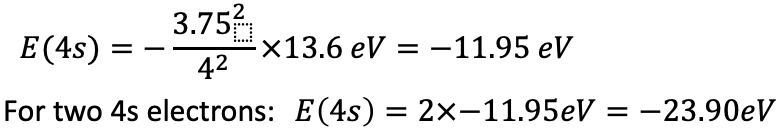
Рівняння 1.2.33 Рівняння енергій електронів 4s в залізі
Сума всіх електронів тоді дорівнює -354,17 еВ + (-23,90 еВ) = -378,1 еВ (ур. 1,2,34).
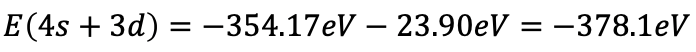
Рівняння 1.2.34 Рівняння для суми всіх електронів
Тепер обчислимо енергію для другої конфігурації електронів. Спочатку нам потрібна ця електронна конфігурація в конфігурації Слейтера. Далі ми можемо обчислити константу екранування для d електронів. Це σ 3d = 7 (0,35) + 18 (1,00) = 20,45, оскільки є сім інших 3d електронів в тій же групі і 18 електронів в нижніх оболонках. Ефективний ядерний заряд тоді Z eff (3d) = 26- 20,45 = 5,55.
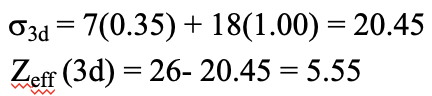
Рівняння 1.2.35 Рівняння для захисного постійного та ефективного ядерного заряду 3d електронів заліза (друга конфігурація)
Сума енергій електронів для восьми d електронів тоді дорівнює E (σ 3d) =-8 (5,55 2 /3 2) Ev=-372,3 еВ, екв. 1.2.36.
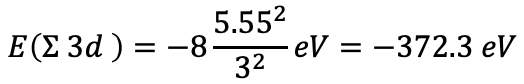
Рівняння 1.2.36 Рівняння для суми енергій електронів для восьми d електронів заліза
Ми можемо бачити, що енергія другої електронної конфігурації дещо вища, і, отже, менш бажана. Це відповідно до експериментально спостережуваного наземного стану електронної конфігурації атома Fe. Знову ж таки, ми бачимо, що правила Слейтера можуть правильно передбачити наземний стан електронної конфігурації атомів.
Принцип Ауфбау та енергія спінового сполучення
Правила Слейтера підходять для обліку екрануючих ефектів у багатоелектронних атомах, які мають електростатичну природу. Однак не тільки електростатичні ефекти впливають на орбітальні енергії, є і магнітні ефекти. Це пояснюється тим, що кожен електрон має спін з пов'язаним з ним магнітним полем. Електрони поводяться як маленькі магніти, які можуть взаємодіяти один з одним. Ці взаємодії можуть бути як привабливими, так і відразливими, що впливає на енергії електронів. Енергії електронів зазвичай мінімізуються, коли кількість електронів з однаковим спіном максимізується. Це відоме як правило Гунда (рис. 1.2.49) максимальної кратності спина.

У попередньому прикладі ми бачили, що електронна конфігурація 4s 2 3d 6 віддається перевагу в Fe через електростатичні екрануючі ефекти. Крім того, йому також сприяють магнітні ефекти. У цій електронній конфігурації є чотири непарних електронів, в той час як в електронній конфігурації 3d 8 є тільки два непарних електронів.
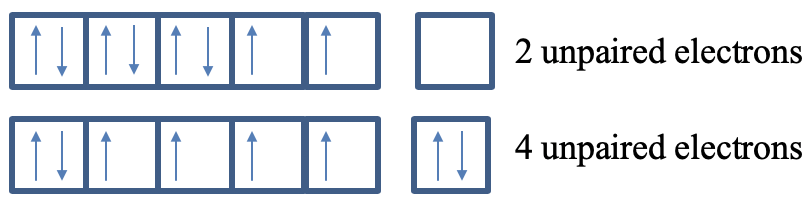
Тепер ми можемо зрозуміти принцип Ауфбау для багатоелектронних атомів (рис. 1.2.51).
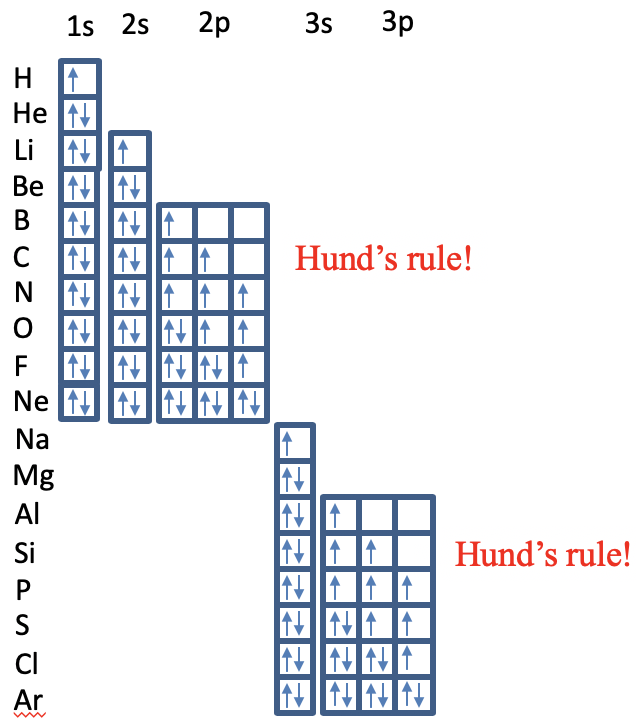
Для Н і Він 1s орбітальний заповнюється. Від літію до берилію 2s підоболонка заповнюється, а від бору до неону 2p підоболонка заповнюється з урахуванням правила Гунда. Ви можете бачити, що для вуглецю два електрони 2p обидва обертаються в різних 2p орбіталів. Для азоту є три непарних електрона на орбіталі 2p. Починаючи з елемента кисню, ми повинні почати спарювання спінів, поки всі спини не будуть спарені в неоні. Від Na до Ar орбіталі 3s і 3p заповнюються за тими ж принципами.
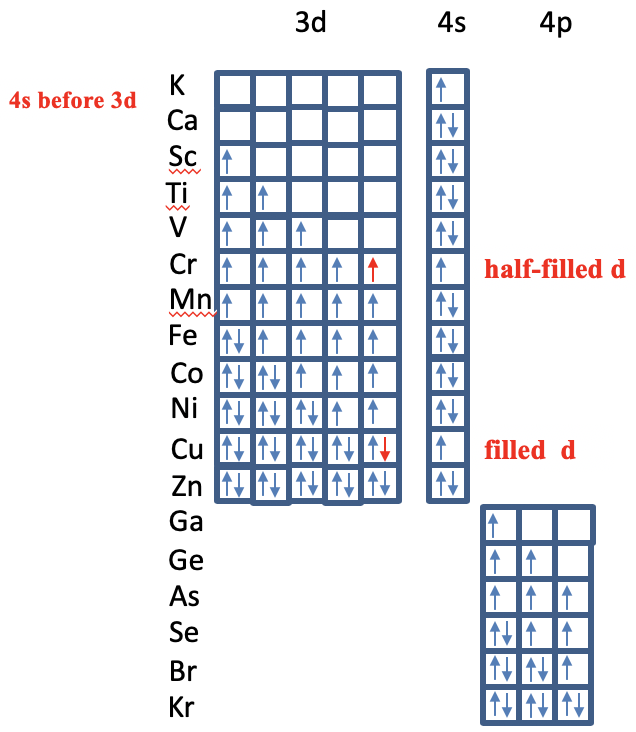
Після цього заповнюються 4s орбіталі K і Ca, а потім 3d орбіталі елементів від Sc до Zn (рис.1.2.52). Раніше ми бачили, що правила Слейтера добре показують, чому. Ви можете бачити, що є дві аномалії, хоча. Для хрому конфігурація електронів становить 4s 1 3d 5, а не 4s 2 3d 4. Це пов'язано з тим, що в цій електронній конфігурації є більше непарних спинив, а напівзаповнена 3d підоболонка з непарними спинами лише представляє особливо стабільну електронну конфігурацію. Друга аномалія виникає для елемента Cu, який має електронну конфігурацію 4s 1 3d 10, а не 4s 2 3d 9. Це пов'язано з тим, що електронна конфігурація d 10 - це особлива стабільна електронна конфігурація. Після заповнення 3d підоболонки, підоболонка 4p заповнюється для елементів від Ga до Kr. Знову ж таки, електрони заповнюються в орбіталі за правилом Гунда. Ми могли б розширити наш розгляд на ще більш важкі елементи, але буде поза сферою дії.
