21.1: Ядерна структура та стабільність
- Page ID
- 22704
- Опишіть ядерну структуру з точки зору протонів, нейтронів та електронів
- Обчислити дефект маси і енергію зв'язування ядер
- Поясніть тенденції відносної стабільності ядер
Ядерна хімія - це вивчення реакцій, які передбачають зміни ядерної структури. Глава про атоми, молекули та іони ввела основну ідею ядерної структури, що ядро атома складається з протонів і, за винятком\(\ce{^1_1H}\), нейтронів. Нагадаємо, що кількість протонів в ядрі називається атомним номером (\(Z\)) елемента, а сума числа протонів і числа нейтронів - числом маси (\(A\)). Атоми з однаковим атомним номером, але різними масовими числами, є ізотопами одного і того ж елемента. Звертаючись до одного типу ядра, ми часто використовуємо термін нуклід і ідентифікуємо його за позначеннями:
\[\ce{^{A}_{Z}X} \label{Eq1} \]
де
- \(X\)є символом елемента,
- \(A\)це масове число, і
- \(Z\)атомний номер.
Часто на нуклід посилається назва елемента, за яким слідує дефіс і число маси. Наприклад,\(\ce{^{14}_6C}\) називається «вуглець-14».
Протони і нейтрони, в сукупності називаються нуклонами, щільно упаковані в ядро. При радіусі близько 10 −15 метрів ядро досить мале в порівнянні з радіусом всього атома, який становить близько 10 −10 метрів. Ядра надзвичайно щільні в порівнянні з сипучою речовиною, усереднення\(1.8 \times 10^{14}\) грамів на кубічний сантиметр. Наприклад, вода має щільність 1 грам на кубічний сантиметр, а іридій, один з найщільніших відомих елементів, має щільність 22,6 г/см 3. Якби щільність землі дорівнювала середній ядерній щільності, радіус землі становив би всього близько 200 метрів (фактичний радіус землі - приблизно\(6.4 \times 10^6\) метри, в 30 000 разів більше). Приклад\(\PageIndex{1}\) демонструє, наскільки велика ядерна щільність може бути в природному світі.
Щільність нейтронної зірки Нейтронні зірки утворюються, коли ядро дуже масивної зірки зазнає гравітаційного колапсу, внаслідок чого зовнішні шари зірки вибухають у наднової. Складені майже повністю з нейтронів, вони є найщільнішими відомими зірками у Всесвіті, щільності яких можна порівняти із середньою щільністю атомного ядра. Нейтронна зірка в далекій галактиці має масу, рівну 2,4 сонячної маси (1 сонячна маса\(M_☉\) = = маса Сонця =\(\mathrm{1.99 \times 10^{30}\; kg}\)) і діаметр 26 км.
- Яка щільність\(\rho\) цієї нейтронної зірки?
- Як щільність цієї нейтронної зірки порівнюється з щільністю уранового ядра, яке має діаметр близько 15 фм (1 фм = 10 —15 м)?
Рішення
Ми можемо розглядати як нейтронну зірку, так і ядро U-235 як сфери. Тоді щільність для обох задається:
\[\rho = \dfrac{m}{V} \nonumber \]
із
\[V = \dfrac{4}{3} \pi r^3 \nonumber \]
(а) Радіус нейтронної зірки\(\mathrm{\dfrac{1}{2}\times 26\; km = \dfrac{1}{2} \times 2.6 \times 10^4\; m = 1.3 \times 10^4\; m}\) так щільність нейтронної зірки становить:
\[ \begin{align*} \rho &= \dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{2.4(1.99 \times 10^{30}\;kg)}{\frac{4}{3} \pi (1.3 \times 10^4m)^3} \\[4pt] &=5.2 \times 10^{17}\;kg/m^3 \end{align*} \nonumber \]
(б) Радіус ядра U-235 дорівнює\(\mathrm{\dfrac{1}{2} \times 15 \times 10^{−15}\;m=7.5 \times 10^{−15}\;m}\), тому щільність ядра U-235 становить:
\[ \begin{align*} \rho &=\dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{235\;amu \left(\frac{1.66 \times 10^{-27}\;kg}{1\;amu}\right)}{ \frac{4}{3} \pi (7.5 \times 10^{-15}m)^3} \\[4pt] &=2.2 \times 10^{17} \; kg/m^3 \end{align*} \nonumber \]
Ці значення досить схожі (той же порядок), але ядро більш ніж в два рази щільніше нейтронної зірки.
Знайдіть щільність нейтронної зірки масою 1,97 мас Сонця і діаметром 13 км, і порівняйте її з щільністю водневого ядра, яке має діаметр 1,75 см (\(\mathrm{1\; fm = 1 \times 10^{–15}\; m}\)).
- Відповідь
-
Щільність нейтронної зірки дорівнює\(\mathrm{3.4 \times 10^{18}\; kg/m^3}\). Щільність водневого ядра становить\(\mathrm{6.0 \times 10^{17}\; kg/m^3}\). Нейтронна зірка в 5,7 рази щільніше водневого ядра.
Щоб утримувати позитивно заряджені протони разом у дуже малому обсязі ядра, потрібні дуже сильні сили притягання, оскільки позитивно заряджені протони сильно відштовхуються один від одного на таких коротких відстанях. Сила тяжіння, яка утримує ядро разом, є сильною ядерною силою. (Сильна сила є однією з чотирьох основних сил, які, як відомо, існують. Інші - електромагнітна сила, гравітаційна сила та ядерна слабка сила.) Ця сила діє між протонами, між нейтронами, і між протонами і нейтронами. Вона сильно відрізняється від електростатичної сили, яка утримує негативно заряджені електрони навколо позитивно зарядженого ядра (тяжіння між протилежними зарядами). На відстанях менше 10 −15 метрів і всередині ядра сильна ядерна сила набагато сильніша, ніж електростатичні відштовхування між протонами; на більших відстанях і поза ядром вона по суті відсутня.
Енергія ядерного зв'язування
Як простий приклад енергії, пов'язаної з сильною ядерною силою, розглянемо атом гелію, що складається з двох протонів, двох нейтронів і двох електронів. Загальна маса цих шести субатомних частинок може бути розрахована як:
\[ \underset{\Large\text{protons}}{(2 \times 1.0073\; \text{amu})} + \underset{\Large\text{neutrons}}{(2 \times 1.0087\; \text{amu})} + \underset{\Large\text{electrons}}{(2 \times 0.00055\; \text{amu})}= 4.0331\; \text{amu }\label{Eq2} \]
Однак мас-спектрометричні вимірювання показують, що маса\(\ce{_2^4 He}\) атома становить 4.0026 аму, що менше, ніж об'єднані маси його шести складових субатомних частинок. Ця різниця між розрахунковими і експериментально виміряними масами відома як масовий дефект атома. У випадку з гелієм дефект маси вказує на «втрату» в масі 4,0331 аму — 4,0026 аму = 0,0305 аму. Втрата маси, що супроводжує утворення атома з протонів, нейтронів та електронів, обумовлені перетворенням тієї маси в енергію, яка еволюціонується при утворенні атома. Енергія ядерного зв'язку - це енергія, що виробляється, коли нуклони атомів пов'язані між собою; це також енергія, необхідна для розбиття ядра на складові його протони та нейтрони. Порівняно з енергіями хімічних зв'язків, енергії ядерного зв'язку значно більші, як ми дізнаємося в цьому розділі. Отже, енергетичні зміни, пов'язані з ядерними реакціями, значно більші, ніж у хімічних реакцій.
Перетворення між масою та енергією найбільш ідентифіковано рівнянням еквівалентності маси та енергії, як стверджував Альберт Ейнштейн:
\[E=mc^2 \label{Eq3} \]
де Е - енергія, m - маса речовини, що перетворюється, а c - швидкість світла у вакуумі. Це рівняння може бути використано для пошуку кількості енергії, яка виникає при перетворенні речовини в енергію. Використовуючи це рівняння еквівалентності маси та енергії, енергія ядерного зв'язку ядра може бути розрахована на основі його масового дефекту, як показано на прикладі\(\PageIndex{2}\). Різноманітні одиниці зазвичай використовуються для енергій ядерної зв'язку, включаючи електронвольти (еВ), причому 1 еВ дорівнює кількості енергії, необхідної для переміщення заряду електрона через різницю електричних потенціалів в 1 вольт, роблячи\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\).
Визначають енергію зв'язку для нукліду\(\ce{^4_2 He}\) в:
- джоулів на моль ядер
- джоулів на ядро
- МеВ на ядро
Рішення
Масовий дефект для\(\ce{^4_2He}\) ядра становить 0,0305 аму, як показано раніше. Визначте енергію зв'язку в джоулі на нуклід за допомогою рівняння масово-енергетичної еквівалентності. Для розміщення запитуваних енергетичних одиниць дефект маси повинен виражатися в кілограмах (нагадаємо, що 1 Дж = 1 кг м 2 /с 2).
(а) По-перше, висловити дефект маси в г/моль. Це легко зробити, враховуючи числову еквівалентність атомної маси (amu) та молярної маси (г/моль), що є результатом визначень аму та моль одиниць (див. Попереднє обговорення в розділі про атоми, молекули та іони, якщо це необхідно). Масовий дефект, таким чином, становить 0,0305 г/моль. Для розміщення одиниць інших членів в рівнянні мас-енергія маса повинна бути виражена в кг, так як 1 Дж = 1 кг м 2 /с 2. Перетворення грамів в кілограми дає масовий дефект\(\mathrm{3.05 \times 10^{–5}\; kg/mol}\). Підстановка цієї величини в рівняння масово-енергетичної еквівалентності дає:
\[\begin{align*} E &=mc^2 \\[4pt] &= \dfrac{3.05 \times 10^{-5}\;kg}{mol} \times \left(\dfrac{2.998 \times 10^8\;m}{s}\right)^2 \\[4pt] &= 2.74×10^{12}\:kg\:m^2s^{-2}mol^{-1} \\[4pt] &=2.74 \times 10^{12}\;J/mol=2.74\: TJ /mol \end{align*} \nonumber \]
(б) Енергія зв'язку для одного ядра обчислюється з молярної енергії зв'язку з використанням числа Авогадро:
\[\begin{align*} E &= 2.74×10^{12}\:J\:mol^{-1}×\dfrac{1\: mol}{6.022×10^{23}\:nuclei} \\[4pt] &=4.55×10^{-12} \: J =4.55\: pJ \end{align*} \nonumber \]
(c) Нагадаємо, що\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\). Використовуючи енергію зв'язку, обчислену в частині (b):
\[\begin{align*} E &= 4.55×10^{-12} \: J× \dfrac{1\: eV}{1.602×10^{-19}\:J} \\[4pt] &=2.84×10^7\:eV=28.4\: MeV \end{align*} \nonumber \]
Яка енергія зв'язку для нукліду\(\ce{^{19}_9F}\) (атомна маса: 18,9984 аму) в МеВ на ядро?
- Відповідь
-
148.4 МеВ
Оскільки енергетичні зміни для розриву та формування зв'язків настільки малі в порівнянні з енергетичними змінами для розриву або формування ядер, зміни маси під час всіх звичайних хімічних реакцій практично не виявляються. Як описано в розділі про термохімію, найбільш енергійні хімічні реакції проявляють ентальпії на порядку тисяч кДж/моль, що еквівалентно масовим відмінностям в нанограммовому діапазоні (10 —9 г). З іншого боку, енергії ядерного зв'язку зазвичай становлять близько мільярдів кДж/моль, що відповідає масовим різницям в міліграмовому діапазоні (10 —3 г).
Ядерна стабільність
Ядро стабільне, якщо воно не може бути перетворено в іншу конфігурацію без додавання енергії ззовні. З тисяч нуклідів, які існують, близько 250 є стабільними. Графік кількості нейтронів проти кількості протонів для стабільних ядер показує, що стабільні ізотопи потрапляють у вузьку смугу. Цей регіон відомий як смуга стабільності (також називається поясом, зоною або долиною стабільності). Пряма лінія на малюнку\(\PageIndex{1}\) представляє ядра, які мають відношення протонів до нейтронів 1:1 (відношення n:p). Відзначимо, що більш легкі стабільні ядра, в цілому, мають рівну кількість протонів і нейтронів. Наприклад, азот-14 має сім протонів і сім нейтронів. Більш важкі стабільні ядра, однак, мають все більше нейтронів, ніж протони. Наприклад: залізо-56 має 30 нейтронів і 26 протонів, співвідношення n:p 1,15, тоді як стабільний нуклідний свинцевий 207 має 125 нейтронів і 82 протонів, співвідношення n:p дорівнює 1,52. Це пояснюється тим, що більші ядра мають більше протонно-протонних відштовхувань і вимагають більшої кількості нейтронів для забезпечення компенсації сильних сил для подолання цих електростатичних відштовхувань і утримання ядра разом.
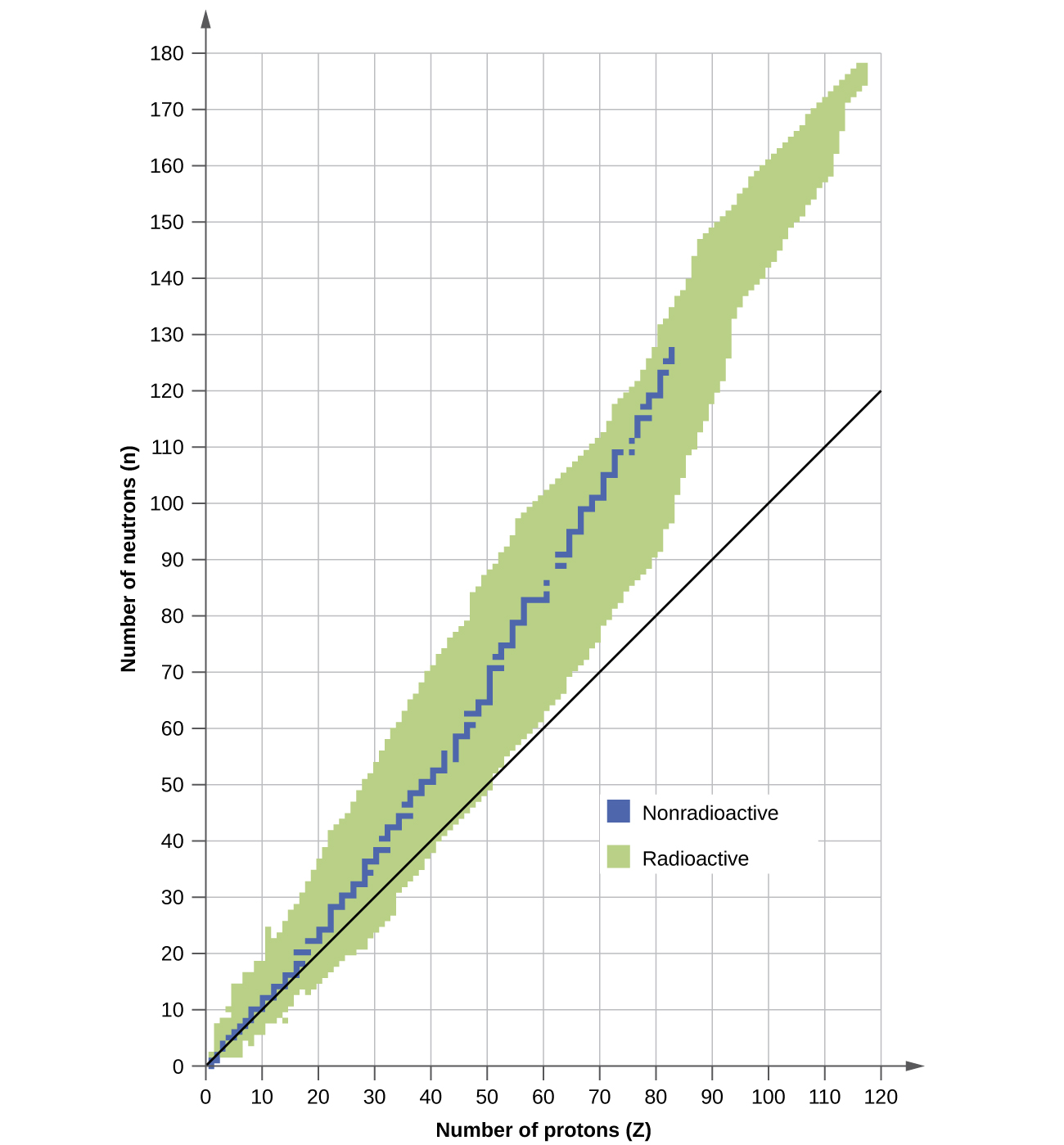
Ядра, які знаходяться зліва або праворуч від смуги стійкості, нестійкі і проявляють радіоактивність. Вони мимовільно змінюються (розпадаються) на інші ядра, які знаходяться або в смузі стабільності, або ближче до неї. Ці ядерні реакції розпаду перетворюють один нестабільний ізотоп (або радіоізотоп) в інший, більш стабільний, ізотоп. Про природу і продукти цього радіоактивного розпаду ми обговоримо в наступних розділах цієї глави.
Можна зробити кілька спостережень щодо зв'язку між стабільністю ядра та його структурою. Ядра з парними числами протонів, нейтронів або обох мають більшу ймовірність стабільності (табл.\(\PageIndex{1}\)). Ядра з певною кількістю нуклонів, відомі як магічні числа, стійкі проти ядерного розпаду. Ці числа протонів або нейтронів (2, 8, 20, 28, 50, 82 і 126) складають повні оболонки в ядрі. Вони схожі за концепцією зі стабільними електронними оболонками, що спостерігаються для благородних газів. Ядра, які мають магічні номери як протонів, так і нейтронів\(\ce{^4_2He}\), такі як\(\ce{^{16}_8O}\)\(\ce{^{40}_{20}Ca}\),, і\(\ce{^{208}_{82}Pb}\) і особливо стабільні. Ці тенденції ядерної стабільності можуть бути раціоналізовані шляхом розгляду квантової механічної моделі станів ядерної енергії, аналогічної тій, яка використовувалася для опису електронних станів раніше в цьому підручнику. Деталі цієї моделі виходять за рамки цієї глави.
| Кількість стабільних ізотопів | Протонне число | Нейтронне число |
|---|---|---|
| 157 | навіть | навіть |
| 53 | навіть | дивно |
| 50 | дивно | навіть |
| 5 | дивно | дивно |
Відносна стабільність ядра корелює з його енергією зв'язування на нуклеон, загальною енергією зв'язку для ядра, поділеною на кількість або нуклонів в ядрі. Наприклад, енергія зв'язку для\(\ce{^4_2He}\) ядра є таким чином:
\[\mathrm{\dfrac{28.4\; MeV}{4\; nucleons}=7.10\; MeV/nucleon} \label{Eq3a} \]
Енергія зв'язку на нуклон нукліду на криву, показану на малюнку\(\PageIndex{2}\)
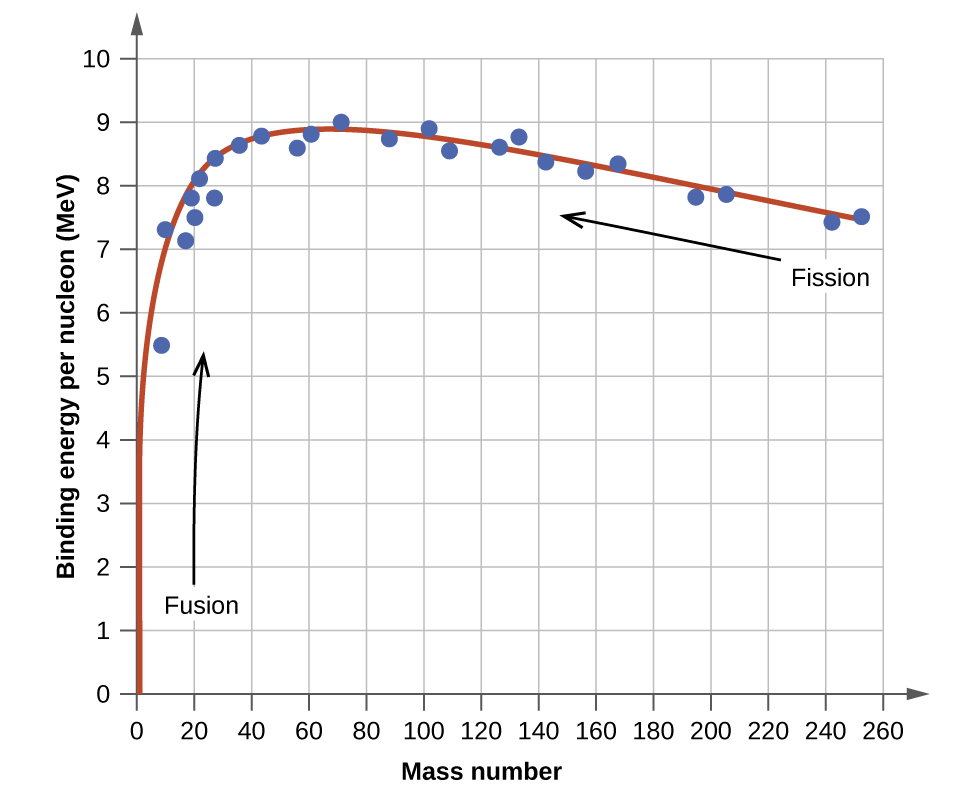
Нуклід заліза\(\ce{^{56}_{26}Fe}\) лежить біля вершини енергетичної кривої зв'язку (рис.\(\PageIndex{2}\)) і є одним з найбільш стійких нуклідів. Яка енергія зв'язування на нуклеон (в МеВ) для нукліду\(\ce{^{56}_{26}Fe}\) (атомна маса 55,9349 аму)?
Рішення
Як і в прикладі, ми спочатку визначаємо дефект маси нукліду, який є різницею між масою 26 протонів, 30 нейтронів і 26 електронів, і спостережуваної масою\(\ce{^{56}_{26}Fe}\) атома:
\ [\ почати {вирівнювати*}
\ матрм {Маса\: дефект} &=\ математика {[(26×1.0073\: аму) + (30×1.0087\: аму) + (26×0.00055\: аму)] −55.9349\: аму}\\
&=\ математика {56.4651\: amu−55.9349\: amu}\\
&=\ mathrm {0.5302\: amu}
\ кінець {вирівнювати*}\ номер\]
Далі обчислюємо енергію зв'язку для одного ядра від дефекту маси за допомогою рівняння масово-енергетичної еквівалентності:
\ [\ почати {вирівнювати*}
E & = mc^2=\ матрм {0.5302\: аму ×\ фрак {1.6605×10^ {-27}\ :кг} {1\: аму} × (2.998×10^8\ :м/с) ^2}\\
&=\ mathrm {7.913×10^ {−11}\:\ текст {кг⋅м} /s^2}\\
&=\ матхрм {7.913×10^ {−11}\ :J}
\ кінець {вирівнювати*}\ номер\]
Потім ми перетворюємо енергію зв'язку в джоулі на ядро в одиниці МеВ на нуклід:
\[\mathrm{7.913×10^{−11}\:J×\dfrac{1\: MeV}{1.602×10^{−13}\:J}=493.9\: MeV} \nonumber \]
Нарешті, визначаємо енергію зв'язку на нуклеон шляхом ділення загальної енергії ядерного зв'язку на кількість нуклонів в атомі:
\[\textrm{Binding energy per nucleon}=\mathrm{\dfrac{493.9\: MeV}{56}=8.820\: MeV/nucleon} \nonumber \]
Зверніть увагу, що це майже на 25% більше, ніж енергія зв'язування на нуклеон для\(\ce{^4_2He}\). (Зауважте також, що це той самий процес, що і в прикладі\ (\ pageIndex {2}\, але з додатковим кроком ділення загальної енергії ядерного зв'язку на кількість нуклонів.)
Яка енергія зв'язування на нуклеон в\(\ce{^{19}_9F}\) (атомна маса, 18.9984 аму)?
- Відповідь
-
7.810 МЕВ/Нуклеон
Резюме
Атомне ядро складається з протонів і нейтронів, які в сукупності називаються нуклонами. Хоча протони відштовхуються один від одного, ядро міцно утримується між собою невеликою дальністю, але дуже сильною силою, яка називається сильною ядерною силою. Ядро має меншу масу, ніж загальна маса входять до його складу нуклонів. Ця «відсутня» маса - це дефект маси, який був перетворений в енергію зв'язку, яка утримує ядро разом відповідно до рівняння еквівалентності маси та енергії Ейнштейна, E = mc 2. З безлічі нуклідів, які існують, стабільними є лише невелика кількість. Особливо схильні до стабільності нукліди з парними числами протонів або нейтронів, або ті, що мають магічні номери нуклонів. Ці стійкі нукліди займають вузьку смугу стійкості на графіку кількості протонів проти кількості нейтронів. Енергія зв'язування на нуклеон найбільша для елементів з масовими числами близько 56; це найбільш стабільні ядра.
Ключові рівняння
- Е = см 2
Глосарій
- смуга стабільності
- (також пояс стійкості, зона стійкості або долина стійкості) область графіка кількості протонів проти кількості нейтронів, що містять стабільні (нерадіоактивні) нукліди
- енергія зв'язування на нуклеон
- загальна енергія зв'язку для ядра, поділена на кількість нуклонів в ядрі
- електрон-вольт (eV)
- одиниця виміру енергій ядерного зв'язку, при цьому 1 еВ дорівнює кількості енергії за рахунок переміщення електрона по різниці електричних потенціалів 1 вольт
- магічне число
- ядра з певними числами нуклонів, які знаходяться в зоні стійкості
- дефект маси
- різниця між масою атома і підсумованою масою складових його субатомних частинок (або маси, «втраченої» при зведенні нуклонів, утворюючи ядро)
- рівняння еквівалентності масової енергії
- Відносини Альберта Ейнштейна показують, що маса та енергія еквівалентні
- ядерна енергія зв'язку
- енергія втрачається, коли нуклони атома пов'язані між собою (або енергія, необхідна для розбиття ядра на складові протони та нейтрони)
- ядерна хімія
- вивчення будови атомних ядер і процесів, що змінюють ядерну структуру
- нуклеон
- колективний термін для протонів і нейтронів в ядрі
- нуклід
- ядро певного ізотопу
- радіоактивності
- явище проявляється нестабільним нуклоном, який спонтанно зазнає зміни в нуклеон, який є більш стабільним; нестабільний нуклеон, як кажуть, радіоактивний
- радіоізотопних
- ізотоп, який є нестабільним і зазнає перетворення в інший, більш стабільний ізотоп
- сильні ядерні сили
- сила тяжіння між нуклонами, що тримає ядро разом
