16.4: Енергія Гіббса
- Page ID
- 22394
- Визначте вільну енергію Гіббса і опишіть її відношення до спонтанності
- Обчисліть стандартну зміну вільної енергії для процесу, використовуючи стандартні вільні енергії формування для його реагентів і продуктів
- Розрахуйте стандартну зміну вільної енергії для процесу з використанням сентальпій освіти та ентропій для його реагентів та продуктів
- Поясніть, як температура впливає на спонтанність деяких процесів
- Пов'язати стандартні зміни вільної енергії з константами рівноваги
Однією з проблем використання другого закону термодинаміки для визначення того, чи є хімічна реакція спонтанною, є те, що ми повинні визначити зміну ентропії для системи та зміну ентропії для оточення. Друга проблема при роботі з хімічною реакцією полягає в тому, що нам потрібно враховувати змішування речовин, питання, яке не виникає при спостереженні зміни фази чистої речовини. Альтернативний підхід, що передбачає нову термодинамічну властивість, визначену лише з точки зору властивостей системи, був введений в кінці дев'ятнадцятого століття американським математиком Джозією Віллардом Гіббсом. Ця нова властивість називається вільна енергія Гіббса (\(G\)) (або просто вільна енергія), і вона визначається з точки зору ентальпії та ентропії системи наступним чином:
\[G=H−TS \nonumber \]
Вільна енергія є функцією стану, і при постійній температурі і тиску стандартна зміна вільної енергії (ΔG°) може виражатися наступним чином:
\[ΔG^º_\ce{sys}=ΔH^º_\ce{sys}−TΔS^º_\ce{sys} \nonumber \]
(Заради простоти, нижній індекс «sys» відтепер буде опущений.) Ми можемо зрозуміти взаємозв'язок між цією системною властивістю та спонтанністю процесу, згадавши раніше виведений другий закон вираз:
\[ΔS_\ce{univ}=ΔS+\dfrac{q_\ce{surr}}{T} \nonumber \]
Перший закон вимагає того\(q_{surr} = −q_{sys}\), і при постійному тиску\(q_{sys} = ΔH\), і тому цей вираз може бути переписано наступним чином:
\[ΔS_\ce{univ}=ΔS−\dfrac{ΔH}{T} \nonumber \]
ΔH - зміна ентальпії системи. Множення обох сторін цього рівняння на −T та перестановка дає наступне:
\[−TΔS_\ce{univ}=ΔH−TΔS \nonumber \]
Порівняння цього рівняння з попереднім для зміни вільної енергії показує наступне співвідношення:
\[ΔG=−TΔS_\ce{univ} \label{6} \]
Отже, зміна вільної енергії є надійним показником спонтанності процесу, безпосередньо пов'язаного з раніше виявленим показником спонтанності\(ΔS_{univ}\). Таблиця\(\PageIndex{1}\) узагальнює зв'язок між спонтанністю процесу і арифметичними ознаками цих показників.
| \(ΔS_{univ} > 0\) | Δ Г < 0 | рухається спонтанно в прямому напрямку, як написано, для досягнення рівноваги |
| \(ΔS_{univ} < 0\) | Δ Г > 0 |
неспонтанний в прямому напрямку, як написано, але рухається спонтанно в зворотному напрямку, як написано, щоб досягти рівноваги |
| \(ΔS_{univ} = 0\) | Δ Г = 0 | оборотний (при рівновазі) |
Розрахунок вільної зміни енергії
Вільна енергія - це функція стану, тому її величина залежить тільки від умов початкового і кінцевого станів системи, які зазнали деяких змін. Зручним і поширеним підходом до розрахунку змін вільної енергії для фізичних змін і хімічних реакцій є використання широко доступних компіляцій стандартних термодинамічних даних стану. Один із методів передбачає використання стандартних ентальпій та ентропій для обчислення стандартних змін вільної енергії відповідно до наступного співвідношення, як показано в прикладі\(\PageIndex{1}\).
\[ ΔG°=ΔH°−TΔS° \label{7} \]
Важливо розуміти, що для фазових змін\(\Delta G^º\) говорить вам, чи є зміна фази спонтанною чи ні; станеться це чи ні. Для хімічних реакцій,\(\Delta G^º\) повідомляє вам ступінь реакції. Іншими словами,\(\Delta G^º\) за реакцію підказує, скільки продукту буде присутній при рівновазі. Реакція з\(\Delta G^º\) <0 вважається сприятливою продуктом при рівновазі; продуктів буде більше, ніж реагентів, коли реакція досягне рівноваги. Реакція\(\Delta G^º\) з> 0 вважається сприятливою для реагентів при рівновазі; реагентів буде більше, ніж продуктів, коли реакція досягне рівноваги.
Використовуйте стандартні дані ентальпії та ентропії з таблиць T1 або T2 для розрахунку стандартної зміни вільної енергії для випаровування води при кімнатній температурі (298 К). Що обчислене значення ΔG° говорить про спонтанність цієї фізичної зміни для чистої речовини?
Рішення
Процес, що цікавить, полягає в наступному:
\[\ce{H2O}(l)⟶\ce{H2O}(g) \label{\(\PageIndex{8}\)} \]
Стандартна зміна вільної енергії може бути розрахована за допомогою наступного рівняння:
\[ΔG^\circ_{298}=ΔH°−TΔS° \label{\(\PageIndex{9}\)} \]
З таблиць T1 або T2 ось дані:
| Речовина | \(ΔH^\circ_\ce{f}\ce{(kJ/mol)}\) | \(S^\circ_{298}\textrm{(J/K⋅mol)}\) |
|---|---|---|
| Н 2 О (л) | \ (ΔH^\ circ_\ ce {f}\ ce {(кДж/моль)}\)» стиль = «вирівнювання тексту: центр;" >−286.83 | \ (S^\ circ_ {298}\ textrm {(Дж/к⋅моль)}\)» style="вирівнювання тексту: центр; ">70.0 |
| Н 2 О (г) | \ (ΔH^\ circ_\ ce {f}\ ce {(кДж/моль)}\)» стиль = «вирівнювання тексту: центр;" >−241,82 | \ (S^\ circ_ {298}\ textrm {(Дж/к⋅моль)}\)» style="вирівнювання тексту: центр; ">188.8 |
Поєднання при 298 К:
\[\begin{align*} ΔH°&=ΔH^\circ_{298}=ΔH^\circ_\ce{f}(\ce{H2O}(g))−ΔH^\circ_\ce{f}(\ce{H2O}(l)) \\[4pt] &=[−241.82\: kJ−(−285.83)]\:kJ/mol \\[4pt] &=44.01\: kJ/mol \\[4pt] ΔS° &=ΔS^\circ_{298}=S^\circ_{298}(\ce{H2O}(g))−S^\circ_{298}(\ce{H2O}(l)) \\[4pt] &=188.8\:J/mol⋅K−70.0\:J/K \\[4pt] &=118.8\:J/mol⋅K \end{align*} \nonumber \]
потім використовуйте Рівняння\ ref {7}:
\[ΔG°=ΔH°−TΔS° \nonumber \]
Перетворення всього в кДж і комбінування при 298 K:
\[\begin{align*}ΔG^\circ_{298} &=ΔH°−TΔS° \\[4pt] &=44.01\: kJ/mol−(298\: K×118.8\:J/mol⋅K)×\dfrac{1\: kJ}{1000\: J} \end{align*} \nonumber \]
\[\mathrm{44.01\: kJ/mol−35.4\: kJ/mol=8.6\: kJ/mol} \nonumber \]
При 298 К (25° С)\(ΔG^\circ_{298}>0\), і так кипіння неспонтанне (не мимовільне) при 298 К.
Використовуйте стандартні дані ентальпії та ентропії з таблиць T1 або T2 для розрахунку стандартної зміни вільної енергії для реакції, показаної тут (298 К). Що говорить обчислене значення ΔG° про ступінь цієї реакції при 298 К?
\[\ce{C2H6}(g)⟶\ce{H2}(g)+\ce{C2H4}(g) \nonumber \]
- Відповідь
-
\(ΔG^\circ_{298}=\mathrm{102.0\: kJ/mol}\); реакція сприяє реагенту при рівновазі при 25° C. буде більше,\(\ce{C2H6}(g)\) ніж\(\ce{H2}(g)\) і\(\ce{C2H4}(g) \) при рівновазі
Зміни вільної енергії також можуть використовувати стандартну вільну енергію освіти для кожного з реагентів і продуктів\( (ΔG^\circ_\ce{f})\), що беруть участь в реакції. Стандартна вільна енергія освіти - це зміна вільної енергії, яке супроводжує утворення одного моля речовини з його елементів в їх стандартних станах. Подібно до стандартних ентальпій освіти,\( (ΔG^\circ_\ce{f})\) є за визначенням нульовим для елементарних речовин в стандартних умовах стану. Підхід до обчислення зміни вільної енергії для реакції з використанням цього підходу такий же, як і раніше для змін ентальпії та ентропії. Для реакції
\[m\ce{A}+n\ce{B}⟶x\ce{C}+y\ce{D}, \nonumber \]
стандартна зміна вільної енергії при кімнатній температурі може бути розрахована як
\[ \begin{align} ΔG^\circ_{298}&=ΔG° \\[4pt] &=∑νΔG^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants})\\[4pt] &=[xΔG^\circ_\ce{f}(\ce{C})+yΔG^\circ_\ce{f}(\ce{D})]−[mΔG^\circ_\ce{f}(\ce{A})+nΔG^\circ_\ce{f}(\ce{B})]. \end{align} \nonumber \]
Розглянемо розкладання жовтого оксиду ртуті (II).
\[\ce{HgO}(s,\,\ce{yellow})⟶\ce{Hg}(l)+ \ce{ 1/2 O2(g)} \nonumber \]
Розрахуйте стандартну вільну зміну енергії при кімнатній температурі\(ΔG^\circ_{298}\), використовуючи:
- стандартні вільні енергії формування і
- стандартні ентальпії освіти і стандартні ентропії.
Чи вказують результати на реакцію, яка буде сприятливою для продукту або реагентом при рівновазі?
Рішення
Необхідні дані доступні в таблицях T1 або T2 і наведені тут.
| З'єднання | \(ΔG^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(ΔH^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(S^\circ_{298}\:\textrm{(J/K⋅mol)}\) |
|---|---|---|---|
| Go (s, жовтий) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(кДж/моль)}\)» стиль = "вирівнювання тексту: центр; ">−58.43 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(кДж/моль)}\)» стиль = "вирівнювання тексту: центр; ">−90.46 | \ (S^\ circ_ {298}\:\ textrm {(Дж/к⋅моль)}\)» style="вирівнювання тексту: центр; ">71.13 |
| Рт.ст. (л) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(кДж/моль)}\)» стиль = "вирівнювання тексту: центр; "> 0 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(кДж/моль)}\)» стиль = "вирівнювання тексту: центр; "> 0 | \ (S^\ circ_ {298}\:\ textrm {(Дж/к⋅моль)}\)» style="вирівнювання тексту: центр; ">75.9 |
| О 2 (г) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(кДж/моль)}\)» стиль = "вирівнювання тексту: центр; "> 0 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(кДж/моль)}\)» стиль = "вирівнювання тексту: центр; "> 0 | \ (S^\ circ_ {298}\:\ textrm {(Дж/к⋅моль)}\)» style="вирівнювання тексту: центр; "> 205.2 |
(а) Використання вільних енергій формування:
\[ \begin{align*} ΔG^\circ_{298}&=∑νGS^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔG^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔG^\circ_{298}\ce{O2}(g)\right]−1ΔG^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\:mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)\right]−1\: mol(−58.43\: kJ/mol)=58.43\: kJ/mol} \end{align*} \nonumber \]
(б) Використання ентальпій та ентропій формування:
\[\begin{align*}ΔH^\circ_{298}&=∑νΔH^\circ_{298}(\ce{products})−∑νΔH^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔH^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔH^\circ_{298}\ce{O2}(g)\right]−1ΔH^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] &\mathrm{=[1\: mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)]−1\: mol(−90.46\: kJ/mol)=90.46\: kJ/mol} \\[4pt] ΔS^\circ_{298} &=∑νΔS^\circ_{298}(\ce{products})−∑νΔS^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔS^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔS^\circ_{298}\ce{O2}(g)\right]−1ΔS^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\: mol(75.9\: J/mol\: K)+\dfrac{1}{2}mol(205.2\: J/mol\: K)\right]−1\: mol(71.13\: J/mol\: K)=107.4\: J/mol\: K} \end{align*} \nonumber \]
то ми можемо використовувати рівняння\ ref7} безпосередньо:
\[\begin{align*}ΔG°&=ΔH°−TΔS°\\[4pt] &=\mathrm{90.46\: kJ−298.15\: K×107.4\: J/K⋅mol×\dfrac{1\: kJ}{1000\: J}} \\[4pt] &=\mathrm{(90.46−32.01)\:kJ/mol=58.45\: kJ/mol} \end{align*} \nonumber \]
Обидва способи розрахунку стандартної зміни вільної енергії при 25° C дають однакове числове значення (до трьох значущих цифр), і обидва прогнозують, що процес є сприятливим для реагентів при рівновазі при кімнатній температурі.
Обчисліть ΔG°, використовуючи (а) вільні енергії освіти і (б) ентальпії освіти і ентропії (таблиці Т1 або Т2). Чи вказують результати на реакцію на користь продукту або реагенту при рівновазі при 25° C?
\[\ce{C2H4}(g)⟶\ce{H2}(g)+\ce{C2H2}(g) \nonumber \]
- Відповідь
-
141,5 кДж/моль, реагент сприятливий при рівновазі
Температурна залежність спонтанності та ступеня реакції
Як було раніше продемонстровано в розділі цього розділу про ентропію, спонтанність процесу може залежати від температури системи. Фазові переходи, наприклад, будуть протікати спонтанно в ту чи іншу сторону залежно від температури речовини, про яку йде мова. Подібним, але не однаковим способом, деякі хімічні реакції можуть переходити від сприятливих продуктів при рівновазі, до реагентів, сприятливих при рівновазі, залежно від температури.
\(\Delta G^º\)Чисельне значення завжди залежить від температури. У цьому розділі ми визначаємо, чи залежить\(\Delta G^º\) ознака від температури.
Для ілюстрації цієї концепції розглядається рівняння, що стосується зміни вільної енергії до ентальпії та ентропії для процесу:
\[ ΔG^º=ΔH^º−TΔS^º \nonumber \]
Ступінь процесу, відображена в арифметичному знаку його стандартної зміни вільної енергії, потім визначається ознаками змін ентальпії та ентропії та, в деяких випадках, абсолютної температури. Оскільки T - абсолютна (Кельвінова) температура, вона може мати тільки позитивні значення. Тому існують чотири можливості щодо ознак змін ентальпії та ентропії:
- Обидва Δ H º і Δ S º є позитивними. Цей стан описує ендотермічний процес, який передбачає збільшення ентропії системи. В цьому випадку Δ G º буде негативним, якщо величина терміна T Δ S º більше, ніж Δ H º. Якщо термін T Δ S º менше, ніж Δ H º, зміна вільної енергії буде позитивним. Такий процес є сприятливим продуктом при рівновазі при високих температурах та сприятливим для реагентів при рівновазі при низьких температурах.
- Обидва Δ Н º і Δ S º є негативними. Цей стан описує екзотермічний процес, який передбачає зниження ентропії системи. В цьому випадку Δ G º буде негативним, якщо величина терміна T Δ S º менше Δ H º. Якщо величина терміна T Δ S º більше, ніж Δ H º, зміна вільної енергії буде позитивною. Такий процес є сприятливим продуктом при рівновазі при низьких температурах та сприятливим для реагентів при рівновазі при високих температурах.
- Δ H º позитивний, а Δ S º негативний. Цей стан описує ендотермічний процес, який передбачає зниження ентропії системи. При цьому Δ G º буде позитивним незалежно від температури. Такий процес є сприятливим для реагентів при рівновазі при всіх температурах.
- Δ H º є негативним, а Δ S º позитивним. Цей стан описує екзотермічний процес, який передбачає збільшення ентропії системи. При цьому Δ G º буде негативним незалежно від температури. Такий процес є сприятливим продуктом при рівновазі при всіх температурах.
Ці чотири сценарії зведені в табл.\(\PageIndex{1}\)
|
Знак\(\Delta H^o\) |
Знак\(\Delta S^o\) |
Знак\(\Delta G^o\) |
Температурна залежність\(\Delta G^o\) |
|---|---|---|---|
| \ (\ Дельта H^o\) ">- | \ (\ Дельта S^o\) ">+ | \ (\ Дельта G^o\) ">- | \ (\ Delta G^o\) ">Знак\(\Delta G^o\) не залежить від температури. Реакція продукту сприятлива при рівновазі при всіх температурах. |
| \ (\ Дельта H^o\) ">+ | \ (\ Дельта S^o\) ">- | \ (\ Дельта Г^О\) ">+ | \ (\ Delta G^o\) ">Знак\(\Delta G^o\) не залежить від температури. Реакція є сприятливою при рівновазі при всіх температурах. |
| \ (\ Дельта H^o\) ">- | \ (\ Дельта S^o\) ">- | \ (\ Дельта G^o\) ">- або + | \ (\ Delta G^o\) ">Знак\(\Delta G^o\) does залежить від температури. Реакція буде сприяти продукту при рівновазі при більш низьких температурах. |
| \ (\ Дельта H^o\) ">+ | \ (\ Дельта S^o\) ">+ | \ (\ Дельта G^o\) ">- або + | \ (\ Дельта G^o\) ">
Ознака\(\Delta G^o\) дійсно залежить від температури. Реакція буде сприяти продукту при рівновазі при більш низьких температурах. |
Неповне згоряння вуглецю описується наступним рівнянням:
\[\ce{2C}(s)+\ce{O2}(g)⟶\ce{2CO}(g) \nonumber \]
Чи залежить\(\Delta G^º\) ознака цього процесу від температури?
Рішення
Процеси горіння екзотермічні (\(ΔH^º < 0\)). Ця особлива реакція передбачає збільшення ентропії за рахунок супутнього збільшення кількості газоподібних видів (чистий приріст одного моля газу\(ΔS^º > 0\)). Тому реакція є сприятливою для продукту при рівновазі (\(ΔG^º < 0\)) при всіх температурах.
Популярні хімічні грілки для рук генерують тепло шляхом повітряного окислення заліза:
\[\ce{4Fe}(s)+\ce{3O2}(g)⟶\ce{2Fe2O3}(s) \nonumber \]
Чи залежить\(\Delta G^o\) ознака цього процесу від температури?
- Відповідь
-
Δ H º і Δ S º є негативними; реакція сприятлива для продукту при рівновазі при низьких температурах.
При розгляді висновків, зроблених щодо температурної залежності знака Δ G º, важливо мати на увазі, що означають терміни «високий» і «низький». Оскільки ці терміни є прикметниками, розглянуті температури вважаються високими або низькими щодо деякої еталонної температури. Процес, який сприяє реагенту при рівновазі при одній температурі, але сприятливий продукт при рівновазі при іншій температурі обов'язково зазнає зміни «ступеня» (як відображено його Δ G º), коли температура змінюється. Це наочно ілюструється графічним поданням рівняння зміни вільної енергії, в якому Δ G º наноситься на вісь y проти T на осі x:
\[ΔG^º=ΔH^º−TΔS^º \nonumber \]
\[y=b+mx \nonumber \]
Такий сюжет показаний на малюнку\(\PageIndex{2}\). Процес, зміни ентальпії та ентропії якого мають один і той же арифметичний знак, буде демонструвати температурну залежність для знака Δ G º, як зображено двома жовтими лініями на графіку. Кожна лінія перетинається з однієї області спонтанності (позитивної або негативної Δ G º) до іншої при температурі, характерній для розглянутого процесу. Ця температура представлена х -перехопленням прямої, тобто значенням T, для якої Δ G º дорівнює нулю:
\[ΔG^º=0=ΔH^º−TΔS^º \nonumber \]
\[T=\dfrac{ΔH^º}{ΔS^º} \nonumber \]
Таким чином, кажучи, що процес є сприятливим продуктом при рівновазі при «високих» або «низьких» температурах означає, що температура вище або нижче, відповідно, та температура, при якій Δ G º для процесу дорівнює нулю.
У цій дискусії ми використовували два різних опису значення знака Δ G º. Ви повинні знати про значення кожного опису.
а) Ступінь реакції: Цей опис використовується для прогнозування співвідношення концентрацій продукту та реагентів при рівновазі. У цьому описі ми використовуємо термодинамічний термін Δ G º, щоб повідомити нам ту ж інформацію, що і постійна рівноваги, K. Коли Δ G º < 0, K > 1, і реакція буде сприятливою для продукту при рівновазі. Коли Δ G º > 0, K < 1, і реакція сприяє реагенту при рівновазі. Коли Δ G º = 0, K = 1, і реакція матиме приблизно рівні кількості продуктів і реагентів при рівновазі. У всіх випадках реакція буде утворювати суміш продуктів і реагентів в рівновазі. Ми використовуємо знак і величину Δ G º, щоб сказати нам, скільки продукту буде зроблено, якщо реакції дозволено досягти рівноваги.
б) Спонтанність: Цей опис набагато складніший, оскільки він включає дві різні інтерпретації того, як відбувається реакція в стандартному стані. Одна інтерпретація передбачає гіпотетичний процес, при якому реакція протікає від вихідної точки чистих реагентів до кінцевої точки чистих продуктів, при цьому всі речовини виділяються у власних ємностях в стандартних умовах стану. У другій, більш реалістичною інтерпретації, реакція починається з усіма реагентами і всіма продуктами в їх стандартному стані в одній ємності. Потім ми дозволяємо цій конкретній суміші реагувати на нескінченно невелику кількість, щоб ми могли отримати швидкість зміни вільної енергії щодо ступеня реакції, коли всі реагенти та продукти змішуються і (по суті) у стандартних станах. Хоча кожна інтерпретація описує різний сценарій реакції, значення різниці вільної енергії і значення швидкості зміни вільної енергії однакові. Якщо Δ G º < 0, ми говоримо, що реакція спонтанна, це означає, що реакція буде протікати в прямому напрямку, як написано, щоб сформувати чисті продукти в їх стандартному стані. Якщо Δ G º > 0, ми говоримо, що реакція неспонтанна, це означає, що реакція буде протікати в зворотному напрямку, як написано, для утворення чистих реагентів у їх стандартному стані. Якщо Δ G º = 0, ми говоримо, що ні реагенти, ні продукти не сприяють утворенню.
Детальну обробку значення Δgº можна знайти в статті «Вільна енергія проти ступеня реакції» Річарда Трептоу, Журнал хімічної освіти, 1996, Том 73 (1), 51-54.
Як визначено в розділі про рідини і тверді речовини, температура кипіння рідини - це температура, при якій її тверда і рідка фази знаходяться в рівновазі (тобто коли випаровування і конденсація відбуваються з однаковими швидкостями). Використовуйте інформацію в таблицях Т1 або Т2 для оцінки температури кипіння води.
Рішення
Цікавим процесом є наступна зміна фази:
Коли цей процес знаходиться в рівновазі, Δ G = 0, тому вірно наступне:
\[0=ΔH°−TΔS°\hspace{40px}\ce{or}\hspace{40px}T=\dfrac{ΔH°}{ΔS°} \nonumber \]
Використовуючи стандартні термодинамічні дані з таблиць T1 або T2,
\ [\ почати {вирівнювати*}
ΔН°&= ΔH^\ circ_\ ce {f} (\ ce {H2O} (г)) −ΔH^\ circ_\ ce {f} (\ ce {H2O} (л))\ номер\\
&=\ mathrm {−241,82\: кДж/моль− (−285.83\ кДж/Моль) = 44.01\: кДж/моль}\ nonчисло
\ кінець {вирівня*}\ nonumber\]
\ [\ почати {вирівнювати*}
ΔS°&=ΔS^\ circ_ {298} (\ ce {H2O} (г)) −ΔS^\ circ_ {298} (\ ce {H2O} (л))\ номер\\\
=\ mathrm {188.8\: Дж/к⋅моль−70,0\: Дж/к⋅моль=118.8\: Дж/к⋅моль}\ nonumber
\ кінець {align*}\ nonumber\]
\[T=\dfrac{ΔH°}{ΔS°}=\mathrm{\dfrac{44.01×10^3\:J/mol}{118.8\:J/K⋅mol}=370.5\:K=97.3\:°C} \nonumber \]
Прийняте значення нормальної температури кипіння води становить 373,2 К (100,0° C), і тому цей розрахунок є розумним узгодженням. Зверніть увагу, що значення для даних про зміни ентальпії та ентропії були отримані зі стандартних даних при 298 K (таблиці T1 або T2.). При бажанні можна отримати більш точні результати за допомогою ентальпії та ентропії змін, визначених при (або принаймні ближче до) фактичної температури кипіння.
Використовуйте інформацію в таблицях T1 або T2 для оцінки температури кипіння CS 2.
- Відповідь
-
313 К (прийняте значення 319 К).
Вільна енергія та рівновага
Зміна вільної енергії для процесу може розглядатися як міра його рушійної сили. Від'ємне значення для Δ G являє собою кінцеву рушійну силу для процесу в прямому напрямку, тоді як позитивне значення являє собою рушійну силу процесу в зворотному напрямку. Коли Δ G дорівнює нулю, пряма і зворотна рушійні сили рівні, і тому процес відбувається в обох напрямках з однаковою швидкістю (система знаходиться в рівновазі).
У розділі про рівновагу коефіцієнт реакції, Q, був введений як зручна міра стану системи рівноваги. Нагадаємо, що Q - це числове значення виразу масової дії для системи, і що ви можете використовувати його значення для визначення напрямку, в якому буде протікати реакція, щоб досягти рівноваги. Коли Q менше постійної рівноваги, K, реакція буде протікати в прямому напрямку до досягнення рівноваги і Q = K. І навпаки, якщо Q > K, процес буде протікати в зворотному напрямку до досягнення рівноваги.
Зміна вільної енергії для процесу, що відбувається з реагентами та продуктами, присутніми в нестандартних умовах, Δ G, пов'язана зі стандартною зміною вільної енергії, Δ G°, відповідно до цього рівняння:
\[ΔG=ΔG°+RT\ln Q \label{eq10A} \]
R - газова константа (8,314 Дж/К моль), T - Кельвін або абсолютна температура, а Q - коефіцієнт реакції. Ми можемо використовувати це рівняння для прогнозування спонтанності процесу за будь-якого заданого набору умов, як показано в прикладі\(\PageIndex{1}\).
Що таке зміна вільної енергії для процесу, показаного тут за заданих умов?
Т = 25° С,\(P_{\ce{N2}}=\mathrm{0.870\: atm}\),\(P_{\ce{H2}}=\mathrm{0.250\: atm}\), і\(P_{\ce{NH3}}=\mathrm{12.9\: atm}\)
\[\ce{2NH3}(g)⟶\ce{3H2}(g)+\ce{N2}(g) \hspace{20px} ΔG°=\mathrm{33.0\: kJ/mol} \nonumber \]
S рішення
Рівняння\ ref {Eq10a} пов'язує зміну вільної енергії зі стандартною зміною вільної енергії та коефіцієнтом реакції і може використовуватися безпосередньо:
\[\begin{align*} ΔG&=ΔG°+RT\ln Q \\[4pt] &=\mathrm{33.0\:\dfrac{kJ}{mol}+\left(8.314\:\dfrac{J}{mol\: K}×298\: K×\ln\dfrac{(0.250^3)×0.870}{12.9^2}\right)}\\[4pt] &=\mathrm{9680\:\dfrac{J}{mol}\:or\: 9.68\: kJ/mol} \end{align*} \nonumber \]
Оскільки обчислене значення для Δ G є позитивним, реакція в цих умовах неспонтанна. Реакція буде протікати в зворотному напрямку, щоб досягти рівноваги.
Обчисліть зміну вільної енергії для цієї ж реакції при 875° C у суміші 5,00 л, що містить 0,100 моль кожного газу. Чи спонтанна реакція в цих умовах?
- Відповідь
-
Δ G = −47 кДж; так, реакція протікає в прямому напрямку, як написано, для досягнення рівноваги.
Для системи в рівновазі Q = K і Δ G = 0, а рівняння\ ref {eq10a} може бути записано як
\[ \underbrace{0=ΔG°+RT\ln K}_{\text{at equilibrium}} \nonumber \]
\[ΔG°=−RT\ln K \label{eq4A} \]
або альтернативно
\[K=e^{−\frac{ΔG°}{RT}} \label{eq4B} \]
Ця форма рівняння забезпечує корисний зв'язок між цими двома істотними термодинамічними властивостями, і вона може бути використана для отримання констант рівноваги від стандартних змін вільної енергії і навпаки. Співвідношення між стандартними змінами вільної енергії і константами рівноваги зведені в табл\(\PageIndex{1}\).
| К | ΔГ° | Коментарі |
|---|---|---|
| < 1 | > 0 | Реагенти більш рясні при рівновазі. |
| = 1 | = 0 | Реагенти і продукти однаково рясні при рівновазі. |
| > 1 | < 0 | Продукти більш рясні при рівновазі. |
Враховуючи, що стандартні вільні енергії утворення Ag + (aq), Cl − (aq) та AgCl (s) складають 77,1 кДж/моль, −131,2 кДж/моль і −109,8 кДж/моль відповідно, обчислити продукт розчинності K sp для AgCl.
Рішення
Реакція інтересу наступна:
\[\ce{AgCl}(s)⇌\ce{Ag+}(aq)+\ce{Cl-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+][Cl- ]} \nonumber \]
Стандартна зміна вільної енергії для цієї реакції спочатку обчислюється з використанням стандартних вільних енергій освіти для її реагентів і продуктів:
\[ \begin{align*} ΔG° =ΔG^\circ_{298} &=[ΔG^\circ_\ce{f}(\ce{Ag+}(aq))+ΔG^\circ_\ce{f}(\ce{Cl-}(aq))]−[ΔG^\circ_\ce{f}(\ce{AgCl}(s))] \\[4pt] &=[77.1\: kJ/mol−131.2\: kJ/mol]−[−109.8\: kJ/mol] \\[4pt] &=55.7\: kJ/mol \end{align*} \nonumber \]
Константа рівноваги для реакції може бути отримана з її стандартної зміни вільної енергії за допомогою Equation\ ref {eQ4b}:
\[\begin{align*} K_\ce{sp}&=e^{−\dfrac{ΔG°}{RT}}=\exp\left(−\dfrac{ΔG°}{RT}\right) \\[4pt] &=\mathrm{\exp\left(−\dfrac{55.7×10^3\:J/mol}{8.314\:J/mol⋅K×298.15\:K}\right)}\\&=\mathrm{\exp(−22.470)=e^{−22.470}=1.74×10^{−10}} \end{align*} \nonumber \]
Використовуйте термодинамічні дані, наведені в таблицях Т1 або Т2, для розрахунку константи рівноваги для дисоціації тетроксиду азоту при 25 °С.
\[\ce{NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \nonumber \]
- Відповідь
-
К = 6,9
Щоб додатково проілюструвати зв'язок між цими двома істотними термодинамічними поняттями, розглянемо спостереження, що реакції спонтанно протікають у напрямку, який в кінцевому підсумку встановлює рівновагу. Як може бути показано шляхом побудови зміни вільної енергії в порівнянні з ступенем реакції (наприклад, як відображено у значенні Q), рівновага встановлюється при мінімізації вільної енергії системи (рис.\(\PageIndex{3}\)). Якщо система присутня з реагентами та продуктами, присутніми в нерівноважних кількостях (Q ≠ K), реакція буде протікати спонтанно в напрямку, необхідному для встановлення рівноваги.
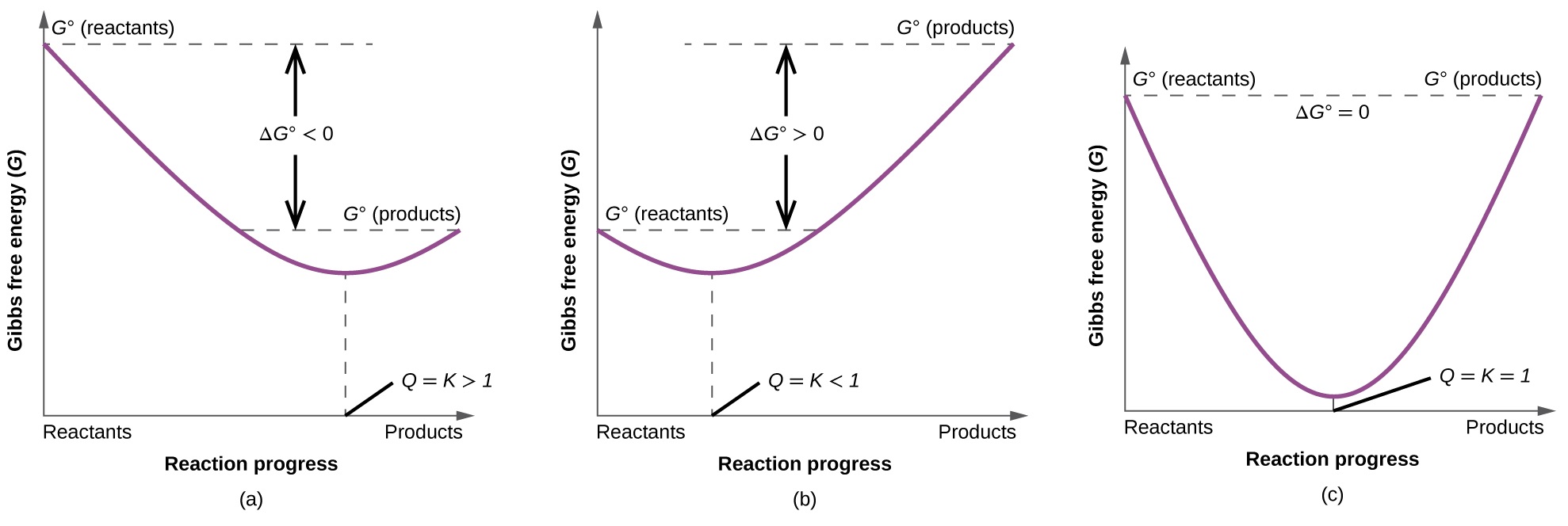
Резюме
Вільна енергія Гіббса (G) - це функція стану, визначена лише стосовно системних величин і може бути використана для прогнозування спонтанності процесу. Від'ємне значення для Δ G вказує на те, що процес буде протікати в прямому напрямку, щоб досягти рівноваги; позитивний Δ G вказує на те, що процес буде протікати в зворотному напрямку, щоб досягти рівноваги; і Δ G нуля вказує на те, що система знаходиться в рівновага. Від'ємне значення для Δ G º означає, що реакція є сприятливою для продукту при рівновазі. Позитивне значення для Δ G º означає, що реакція сприяє реагенту при рівновазі. Якщо Δ G º дорівнює 0 (рідкісне явище), реакція має приблизно рівні кількості реагентів і продуктів при рівновазі.Можлива кількість підходів до обчислення змін вільної енергії.
Ключові рівняння
- Δ Г = Δ Н − Т Δ S
- Δ Г = Δ Г° + РТ на Q
- Δ Г° = − RT пн К
Глосарій
- Зміна вільної енергії Гіббса (G)
- термодинамічна властивість визначається з точки зору ентальпії та ентропії системи; всі спонтанні процеси пов'язані зі зниженням G
- стандартна зміна вільної енергії (Δ G°)
- зміна вільної енергії для процесу, що відбувається в стандартних умовах (тиск 1 бар для газів, концентрація 1 М для розчинів)
- стандартна вільна енергія формування\( (ΔG^\circ_\ce{f})\)
- зміна вільної енергії, що супроводжує утворення одного моля речовини з його елементів в їх стандартних станах
