14.7: Кислотно-лужне титрування

Last updated
Save as PDF

Page ID: 22794

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Інтерпретувати криві титрування сильних і слабких кислотно-лужних систем
Обчислити рН зразка на важливих етапах титрування
Поясніть функцію кислотно-лужних показників

Як видно з розділу про стехіометрії хімічних реакцій, титрування можуть бути використані для кількісного аналізу розчинів на їх кислотні або базові концентрації. У цьому розділі ми вивчимо зміни концентрацій кислих та основних видів, присутніх у розчині в процесі титрування.

Криві титрування

Раніше, коли ми вивчали кислотно-лужні реакції в розчині, ми зосереджувалися лише на точці, в якій кислота і основа були стехіометрично еквівалентні. Не враховувався рН розчину до, під час або після нейтралізації.

Приклад\(\PageIndex{1}\): Calculating pH for Titration Solutions: Strong Acid/Strong Base

Титрування проводять для 25,00 мл 0,100 М HCl (сильної кислоти) з 0,100 М міцної основи NaOH крива титрування показана на рис\(\PageIndex{1}\). Розрахуйте рН при таких обсягах доданого базового розчину:

0,00 мл
12.50 мл
25.00 мл
37,50 мл

Рішення

Оскільки HCl є сильною кислотою, можна припустити, що вся вона дисоціює. Початкова концентрація Н ₃ О ⁺ становить\(\ce{[H3O+]_0}=0.100\:M\). При додаванні базового розчину він також повністю дисоціює, забезпечуючи OH ⁻ іони. Іони H ₃ O ⁺ і OH ⁻ нейтралізують один одного, тому залишаються лише ті з двох, які були в надлишку, а їх концентрація визначає рН. Таким чином, розчин спочатку кислий (рН < 7), але з часом всі іони гідронію, присутні з вихідної кислоти, нейтралізуються, і розчин стає нейтральним. У міру додавання більшої кількості підстави розчин виходить основним.

Загальна початкова кількість іонів гідронію становить:

\[\mathrm{n(H^+)_0=[H_3O^+]_0×0.02500\: L=0.002500\: mol} \nonumber \]

Після додавання X мл базового розчину 0.100- M кількість молів введеного OH ⁻ іонів становить:

\[\mathrm{n(OH^-)_0=0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

Загальний обсяг стає:

\[V=\mathrm{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

Число родимок Н ₃ О ⁺ стає:

\[\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0=0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

Концентрація Н ₃ О ⁺ становить:

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{V}=\dfrac{0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

\[\mathrm{=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×X\: mL}{25.00\: mL+X\: mL}} \nonumber \]

з визначенням\(\mathrm{pH}\):

\[\mathrm{pH=−\log([H_3O^+])} \label{phdef} \]

Попередні розрахунки працюють, якщо\(\mathrm{n(H^+)_0-n(OH^-)_0>0}\) і так n (H ⁺) > 0. Коли\(\mathrm{n(H^+)_0=n(OH^-)_0}\), іони H ₃ O ⁺ з кислоти і ОН ⁻ іони з основи взаємно нейтралізують. На даний момент єдиними іонами гідронію залишилися від автоіонізації води, і немає OH ⁻ частинок, щоб їх нейтралізувати. Тому в цьому випадку:

\[\ce{[H3O+]}=\ce{[OH- ]},\:\ce{[H3O+]}=K_\ce{w}=1.0\times 10^{-14};\:\ce{[H3O+]}=1.0\times 10^{-7} \nonumber \]

\[\mathrm{pH=-log(1.0\times 10^{-7})=7.00} \nonumber \]

Нарешті, коли\(\mathrm{n(OH^-)_0>n(H^+)_0}\), не вистачає іонів H ₃ O ⁺, щоб нейтралізувати всі OH ⁻ іони, і замість\(\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0}\) цього ми обчислюємо:\(\mathrm{n(OH^-)=n(OH^-)_0-n(H^+)_0}\)

У цьому випадку:

\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)-0.002500\: mol}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

\[\mathrm{=\dfrac{0.100\:\mathit{M}×X\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+X\: mL}} \nonumber \]

потім за допомогою визначення\(pOH\) та його співвідношення з водними\(pH\) розчинами кімнатної температури (Equation\ ref {phdef}):

\[\begin{align} pH &=14-pOH \nonumber \\&=14+\log([OH^-]) \nonumber\end{align} \nonumber \]

Розглянемо тепер чотири конкретних випадки, представлені в цій проблемі:

(а) Х = 0 мл

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL}=0.1\:\mathit{M}} \nonumber \]

потім за допомогою визначення\(pH\) (Рівняння\ ref {phdef}):

\[\begin{align} pH &= −\log(0.100) \nonumber \\ &= 1.000 \nonumber\end{align} \nonumber \]

(б) Х = 12,50 мл

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×12.50\: mL}{25.00\: mL+12.50\: mL}=0.0333\:\mathit{M}} \nonumber \]

потім за допомогою визначення\(pH\) (Рівняння\ ref {phdef}):

\[ \begin{align} pH &= −\log(0.0333) \nonumber \\ &= 1.477 \nonumber\end{align} \nonumber \]

(с) Х = 25,00 мл

Так як обсяги і концентрації кислотних і базових розчинів однакові:

\[\mathrm{n(H^+)_0=n(OH^-)_0} \nonumber \]

\[pH = 7.000 \nonumber \]

як описано раніше.

(г) Х = 37,50 мл

У цьому випадку:

\[\mathrm{n(OH^-)_0>n(H^+)_0} \nonumber \]

\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×35.70\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+37.50\: mL}=0.0200\:\mathit{M}} \nonumber \]

потім за допомогою визначення\(pH\) (Рівняння\ ref {phdef}):

\[ \begin{align}[pH = 14 − pOH \nonumber\\ &= 14 + \log([OH^{−}]) \nonumber \\ &= 14 + \log(0.0200) \nonumber \\ &= 12.30 \nonumber \end{align} \nonumber \]

Вправа\(\PageIndex{1}\)

Розрахуйте рН для титрування сильної кислоти/сильної основи між 50,0 мл 0,100 M HNO ₃ (aq) і 0,200 M NaOH (титрант) при перерахованих обсягах доданої основи:

0,00 мл,
15,0 мл,
25,0 мл, а
40,0 мл.

Відповідь на: 0.00:1.000
Відповідь б: 15,0:1 5111
Відповідь c: 25.0:7е. Не видаляйте цей текст спочатку.
Відповідь d: 40,0:12,523

У прикладі\(\PageIndex{1}\) ми розрахували рН у чотирьох точках під час титрування. У таблиці\(\PageIndex{1}\) наведена докладна послідовність змін рН сильної кислоти і слабкої кислоти при титруванні з NaOH.

Таблиця\(\PageIndex{1}\): Значення рН при титруванні сильної кислоти з сильною основою і слабкої кислоти з сильною основою
Обсяг 0,100 М Додано NaOH (мл)	Кроти NaOH Додано	Значення рН 0,100 М HCl ¹	Значення рН 0,100 М\(CH_3CO_2H\) ²
0.0	0.0	1.00	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 2.87
5.0	0.00050	1.18	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 4.14
10.0	0,00100	1.37	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 4.57
15,0	0,00150	1.60	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 4.92
20.0	0,00200	1,95	\ (CH_3CO_2H\) 2" style="вирівнювання тексту: центр; "> 5.35
22.0	0,00220	2.20	\ (CH_3CO_2H\) 2" style="вирівнювання тексту: центр; "> 5.61
24.0	0,00240	2.69	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 6.13
24.5	0,00245	3.00	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 6.44
24.9	0,00249	3.70	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 7.14
25.0	0,00250	7.00	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 8.72
25.1	0,00251	10.30	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 10.30
25.5	0,00255	11.00	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 11.00
26.0	0,00260	11.29	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 11.29
28.0	0,00280	11.75	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 11.75
30.0	0,00300	11.96	\ (CH_3CO_2H\) 2" стиль = "вирівнювання тексту: центр; "> 11.96
35.0	0,00350	12.22	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 12.22
40.0	0,00400	12.36	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 12.36
45.0	0,00450	12.46	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 12,46
50.0	0,00500	12.52	\ (CH_3CO_2H\) 2" стиль = «вирівнювання тексту: центр;" > 12.52
\ (CH_3CO_2H\) 2" style="вирівнювання тексту: центр; "> Титрування 25,00 мл 0,100 М HCl (0,00250 моль HCL) з 0,100 М NaOH. Титрування 25,00 мл 0,100 М СН ₃ СО ₂ Н (0,00250 моль СН ₃ СО ₂ Н) з 0,100 М NaOH.

Найпростіші кислотно-лужні реакції - це сильна кислота з сильною основою. У таблиці\(\PageIndex{1}\) наведені дані для титрування 25,0-мл проби 0,100 М соляної кислоти з 0,100 М гідроксиду натрію. Значення рН, виміряні після послідовного додавання невеликих кількостей NaOH, наведені в першому стовпці цієї таблиці, і зображені на малюнку\(\PageIndex{1}\), у вигляді, який називається кривою титрування. РН збільшується спочатку повільно, швидко зростає в середній частині кривої, а потім знову повільно збільшується. Точка перегину (розташована в середній точці вертикальної частини кривої) - точка еквівалентності титрування. Він вказує, коли присутні еквівалентні кількості кислоти та основи. Для титрування сильної кислоти з сильною основою точка еквівалентності настає при рН 7,00 і точки на кривій титрування можна розрахувати за допомогою стехіометрії розчину (Таблиця\(\PageIndex{1}\) і рис.\(\PageIndex{1}\)).

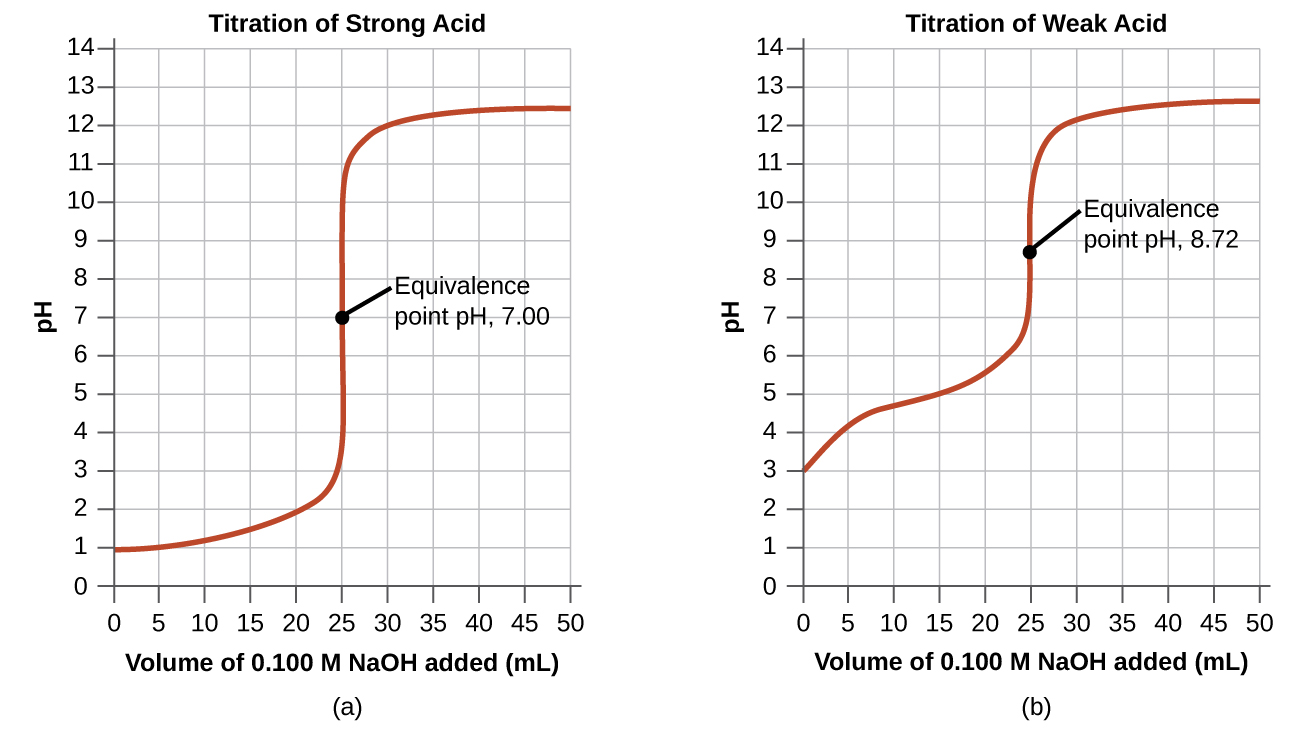
Рисунок\(\PageIndex{1}\): (а) Крива титрування для титрування 25,00 мл 0,100 М HCl (сильна кислота) з 0.100 M NaOH (сильна основа) має точку еквівалентності 7,00 рН. (б) Крива титрування для титрування 25,00 мл 0,100 М CH ₃ CO ₂ H (слабка кислота) з 0,100 М NaOH (сильна основа) має точку еквівалентності 8,72 рН.

Титрування слабкої кислоти з міцною основою (або слабкої основи з сильною кислотою) дещо складніше, ніж тільки що обговорювалося, але воно слідує тим же загальним принципам. Розглянемо титрування 25,0 мл 0,100 М оцтової кислоти (слабкої кислоти) з 0,100 М гідроксиду натрію і порівняємо криву титрування з кривою титрування сильної кислоти. Таблиця\(\PageIndex{1}\) дає значення рН при титруванні, на малюнку\(\PageIndex{1b}\) показана крива титрування.

Хоча початковий об'єм і молярність кислот однакові, між двома кривими титрування існують важливі відмінності. Крива титрування для слабкої кислоти починається з більш високого значення (менш кислотного) і підтримує більш високі значення рН аж до точки еквівалентності. Це пояснюється тим, що оцтова кислота є слабкою кислотою, яка іонізується лише частково. РН в точці еквівалентності також вище (8,72, а не 7,00) через гідролізу ацетату, слабкої основи, що підвищує рН:

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(l)+\ce{OH-}(aq) \nonumber \]

Після точки еквівалентності дві криві ідентичні, оскільки рН залежить від надлишку гідроксид-іона в обох випадках.

Приклад\(\PageIndex{2}\): Titration of a Weak Acid with a Strong Base

Крива титрування, показана на малюнку,\(\PageIndex{1b}\) призначена для титрування 25,00 мл 0,100 M CH ₃ CO ₂ H з 0.100 M NaOH. Реакцію можна уявити у вигляді:

\[\ce{CH3CO2H + OH- ⟶ CH3CO2- + H2O} \nonumber \]

Який початковий рН до додавання будь-якої кількості розчину NaOH? К _а = 1,8 × 10 ⁻⁵ для СН ₃ СО ₂ Н.
Знайдіть рН після додавання 25,00 мл розчину NaOH.
Знайдіть рН після додавання 12,50 мл розчину NaOH.
Знайдіть рН після того, як було додано 37,50 мл розчину NaOH.

Рішення

(а) Припускаючи, що дисоційована сума невелика порівняно з 0.100 M, ми виявляємо, що:

\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}≈\ce{\dfrac{[H3O+]^2}{[CH3CO2H]_0}} \nonumber \]

\[\ce{[H3O+]}=\sqrt{K_\ce{a}×\ce{[CH3CO2H]}}=\sqrt{1.8\times 10^{-5}×0.100}=1.3\times 10^{-3} \nonumber \]

\[\mathrm{pH=-\log(1.3\times 10^{-3})=2.87} \nonumber \]

(б) Після додавання 25,00 мл NaOH кількість молів NaOH і CH ₃ CO ₂ H дорівнює, оскільки кількості розчинів і їх концентрації однакові. Усі CH ₃ CO ₂ H було перетворено в\(\ce{CH3CO2-}\). Концентрація\(\ce{CH3CO2-}\) іона становить:

\[\mathrm{\dfrac{0.00250\: mol}{0.0500\: L}=0.0500\: \ce{MCH3CO2-}} \nonumber \]

Рівновага, на якій слід зосередитися зараз, є рівновагою основності для\(\ce{CH3CO2-}\):

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \nonumber \]

тому ми повинні визначити K _b для основи, використовуючи постійну іонного продукту для води:

\[K_\ce{b}=\ce{\dfrac{[CH3CO2H][OH- ]}{[CH3CO2- ]}} \nonumber \]

\[K_\ce{a}=\ce{\dfrac{[CH3CO2- ][H+]}{[CH3CO2H]}},\textrm{ so }\ce{\dfrac{[CH3CO2H]}{[CH3CO2- ]}}=\dfrac{\ce{[H+]}}{K_\ce{a}}. \nonumber \]

Оскільки K _w = [H ⁺] [ОН ⁻]:

\[\begin{align} K_\ce{b} &=\dfrac{\ce{[H+][OH- ]}}{K_\ce{a}} \\ &=\dfrac{K_\ce{w}}{K_\ce{a}} \\ &=\dfrac{1.0\times 10^{-14}}{1.8\times 10^{-5}} \\ &=5.6\times 10^{-10} \end{align} \nonumber \]

Позначимо концентрацію кожного з продуктів цієї реакції, СН ₃ СО ₂ Н і ОН ⁻, як х. Використовуючи припущення, що х малий в порівнянні з 0,0500 М\(K_\ce{b}=\dfrac{x^2}{0.0500\:M}\), а потім:

\[x=\ce{[OH- ]}=5.3\times 10^{−6} \nonumber \]

\[\ce{pOH}=-\log(5.3\times 10^{-6})=5.28 \nonumber \]

\[\ce{pH}=14.00−5.28=8.72 \nonumber \]

Зверніть увагу, що рН в точці еквівалентності цього титрування значно перевищує 7.

(c) В (а) було додано 25,00 мл розчину NaOH, і тому практично всі CH ₃ CO ₂ H були перетворені в\(\ce{CH3CO2-}\). При цьому введено всього 12,50 мл базового розчину, і тому тільки половина всіх СН ₃ СО ₂ Н перетворюється в\(\ce{CH3CO2-}\). Загальна початкова кількість молів СН ₃ СО ₂ Н становить 0,02500Л × 0,100 М = 0,00250 моль, і тому після додавання NaOH числа родимок СН ₃ СО ₂ Н і\(\ce{CH3CO2-}\) обидва приблизно рівні\(\mathrm{\dfrac{0.00250\: mol}{2}=0.00125\: mol}\), і їх концентрації однакові.

Оскільки кількість доданої основи менше початкової кількості кислоти, точка еквівалентності не досягнута, розчин залишається буфером, і ми можемо використовувати рівняння Гендерсона-Хассельбальха:

\(\ce{pH}=\ce p K_\ce{a}+\log\ce{\dfrac{[Base]}{[Acid]}}=-\log(\mathit{K}_\ce{a})+\log\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]}}=-\log(1.8\times 10^{-5})+\log(1)\)

(так як концентрації СН _{3\(\ce{CH3CO2-}\)} і СО ₂ Н однакові)

Таким чином:

\[\ce{pH}=−\log(1.8\times 10^{−5})=4.74 \nonumber \]

(рН = р К _а на півдорозі при титруванні слабкої кислоти)

(г) Після додавання 37,50 мл NaOH кількість NaOH становить 0,03750 л × 0,100 М = 0,003750 моль NaOH. Оскільки це минуло точку еквівалентності, надлишок іонів гідроксиду зробить розчин основним, і ми можемо знову використовувати стехіометричні розрахунки для визначення рН:

\(\mathrm{[OH^-]=\dfrac{(0.003750\: mol−0.00250\: mol)}{0.06250\: L}}=2.00\times 10^{−2}\:M\)

Отже:

\(\mathrm{pOH=−\log(2.00\times 10^{−2})=1.70,\: and\: pH=14.00−1.70=12.30}\)

Зверніть увагу, що цей результат такий же, як і для наведеного прикладу титрування сильної кислотної основи, оскільки кількість доданої міцної основи переміщує розчин повз точку еквівалентності.

Вправа\(\PageIndex{2}\)

Розрахуйте рН для титрування слабкої кислоти/сильної основи між 50,0 мл 0,100 M HCOOH (aq) (мурашина кислота) і 0,200 M NaOH (титрант) при перерахованих обсягах доданої основи:

0,00 мл,
15,0 мл,
25,0 мл, а
30.0 мл.

Відповідь на: 0,00 мл: 2,37
Відповідь б: 15,0 мл: 3,92
Відповідь c: 25.00 мл: 8.29
Відповідь d: 30,0 мл: 12,097

Кислотно-лужні показники

Деякі органічні речовини змінюють колір в розведеному розчині, коли концентрація іонів гідронію досягає певного значення. Наприклад, фенолфталеїн - безбарвна речовина в будь-якому водному розчині з концентрацією іонів гідронію більше 5,0 × 10 ⁻⁹ М (рН < 8,3). У більш основних розчинах, де концентрація іонів гідронію менше 5,0 × 10 ⁻⁹ М (рН > 8,3), вона буває червоною або рожевою. Такі речовини, як фенолфталеїн, за допомогою яких можна визначити рН розчину, називають кислотно-лужними показниками. Кислотно-лужні показники - це або слабкі органічні кислоти, або слабкі органічні основи.

Рівновага в розчині кислотно-лужного показника метилового апельсина, слабкої кислоти, може бути представлено рівнянням, в якому ми використовуємо\(\ce{HIn}\) як просте уявлення для складної молекули метилового апельсина:

\[\underbrace{\ce{HIn (aq)}}_{\ce{red}}+\ce{H2O (l)}⇌\ce{H3O^{+} (aq)}+\underbrace{\ce{In^{-} (aq)}}_{\ce{yellow}} \nonumber \]

\[K_\ce{a}=\ce{\dfrac{[H3O+][In- ]}{[HIn]}}=4.0\times 10^{−4} \nonumber \]

Аніон метилового апельсина\(\ce{In^{-}}\), жовтий, а неіонізована форма - червоний.\(\ce{HIn}\) Коли ми додаємо кислоту до розчину метилового апельсина, підвищена концентрація іонів гідронію зміщує рівновагу до неіонізованої червоної форми, відповідно до принципу Ле Шательє. Якщо додати базу, зміщуємо рівновагу в сторону жовтої форми. Така поведінка повністю аналогічно дії буферів.

Колір індикатора є видимим результатом співвідношення концентрацій двох видів In ⁻ і\(\ce{HIn}\). Якщо більша частина показника (зазвичай близько 60− 90% або більше) присутня як\(\ce{In^{-}}\), то ми бачимо колір\(\ce{In^{-}}\) іона, який буде жовтим для метилового оранжевого. Якщо більшість присутній як\(\ce{HIn}\), то ми бачимо колір\(\ce{HIn}\) молекули: червоний для метилового оранжевого. Для метилового апельсина ми можемо переставити рівняння для K _a і записати:

\[\mathrm{\dfrac{[In^-]}{[HIn]}=\dfrac{[substance\: with\: yellow\: color]}{[substance\: with\: red\: color]}=\dfrac{\mathit{K}_a}{[H_3O^+]}} \label{ABeq2} \]

Рівняння\ ref {abeQ2} показує нам, як співвідношення\(\ce{\dfrac{[In- ]}{[HIn]}}\) змінюється в залежності від концентрації іона гідронію. Вищевказане вираз, що описує рівновагу індикатора, можна переставити:

\[ \begin{align} \dfrac{[H_3O^+]}{\mathit{K}_a} &=\dfrac{[HIn]}{[In^- ]} \\[8pt] \log\left(\dfrac{[H_3O^+]}{\mathit{K}_a}\right) &= \log\left(\dfrac{[HIn]}{[In^- ]}\right) \\[8pt] \log([H_3O^+])-\log(\mathit{K}_a) &=-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] -pH+p\mathit{K}_a & =-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] pH &=p\mathit{K}_a+\log\left(\dfrac{[In^-]}{[HIn]}\right) \end {align} \nonumber \]

або в загальних рисах

\[pH=p\mathit{K}_a+\log\left(\dfrac{[base]}{[acid]}\right) \label{HHeq} \]

Рівняння\ ref {hHeQ} таке ж, як і рівняння Гендерсона-Хассельбальха, яке може бути використано для опису рівноваги показників.

Коли [H ₃ O ⁺] має таке ж числове значення, що і K _a, відношення [In ⁻] до [HiN] дорівнює 1, тобто 50% показника присутній у червоній формі (HiN), а 50% - в жовтій іонній формі (In ⁻), і розчин з'являється помаранчевий за кольором. При збільшенні концентрації іонів гідронію до 8 × 10 ⁻⁴ М (рН 3,1) розчин стає червоним. Ніяких змін кольору не видно при подальшому збільшенні концентрації іонів гідронію (зниження рН). При концентрації іонів гідронію 4 × 10 ⁻⁵ М (рН 4,4) більша частина показника знаходиться в жовтій іонній формі, а подальше зниження концентрації іонів гідронію (підвищення рН) не призводить до видимої зміни кольору. Діапазон рН між 3,1 (червоний) і 4,4 (жовтий) є інтервалом зміни кольору метилового оранжевого; виражена зміна кольору відбувається між цими значеннями рН.

Існує безліч різних кислотно-лужних показників, які охоплюють широкий діапазон значень рН і можуть бути використані для визначення приблизного рН невідомого розчину шляхом процесу усунення. Універсальні індикатори і pH папір містять суміш показників і демонструють різні кольори при різних рН. \(\PageIndex{2}\)На малюнку представлено кілька показників, їх кольори та інтервали зміни кольору.

альт — Малюнок\(\PageIndex{2}\): Ця діаграма ілюструє діапазони зміни кольору для декількох кислотно-лужних показників.

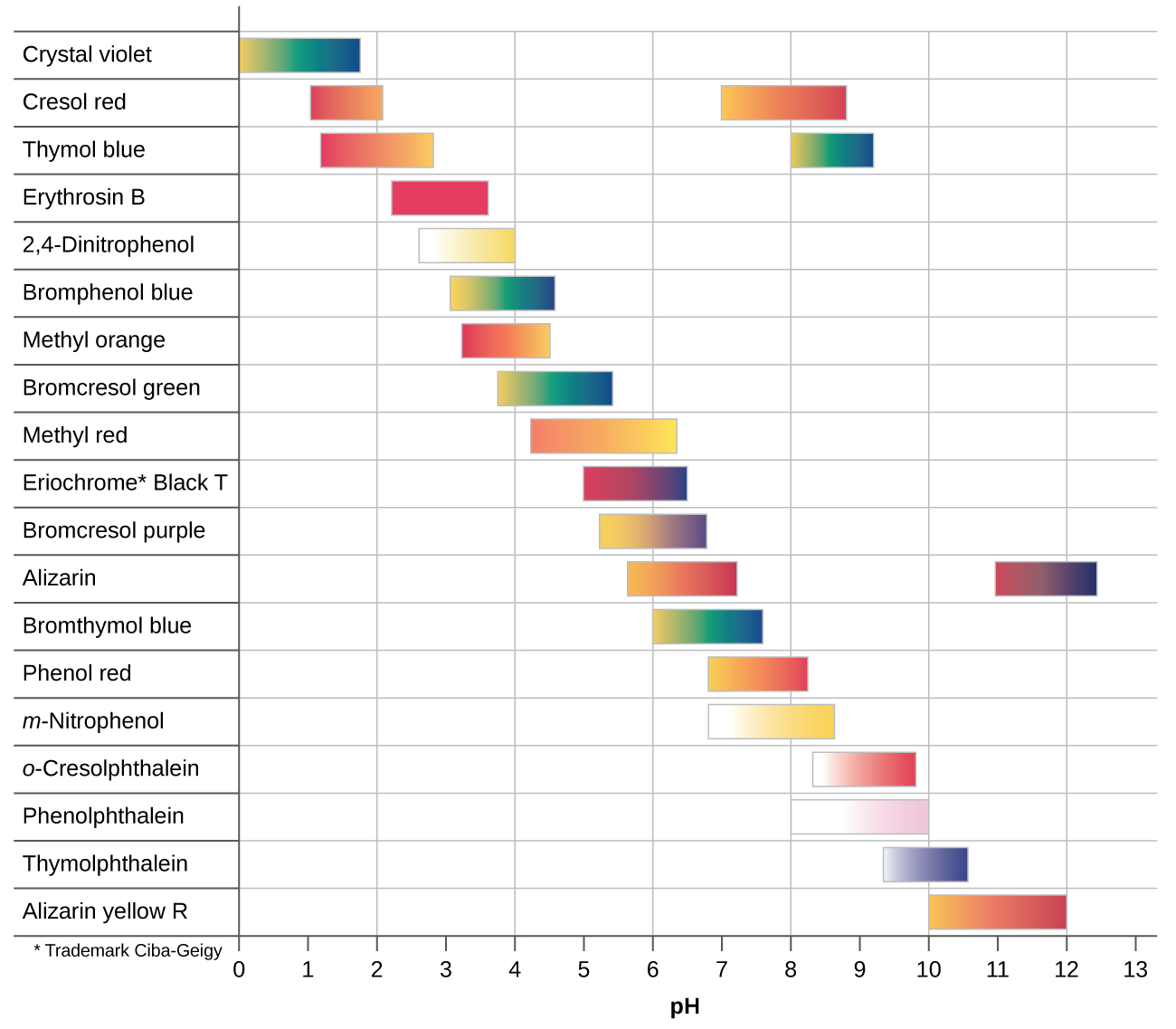
Криві титрування допомагають нам вибрати індикатор, який забезпечить різку зміну кольору в точці еквівалентності. Найкращим вибором буде індикатор, який має інтервал зміни кольору, який дугує рН у точці еквівалентності титрування.

Інтервали зміни кольору трьох показників показані на малюнку\(\PageIndex{3}\). Точки еквівалентності як титрування сильної кислоти, так і слабкої кислоти розташовані в інтервалі зміни кольору фенолфталеїну. Ми можемо використовувати його для титрування або сильної кислоти з сильною основою, або слабкої кислоти з сильною основою.

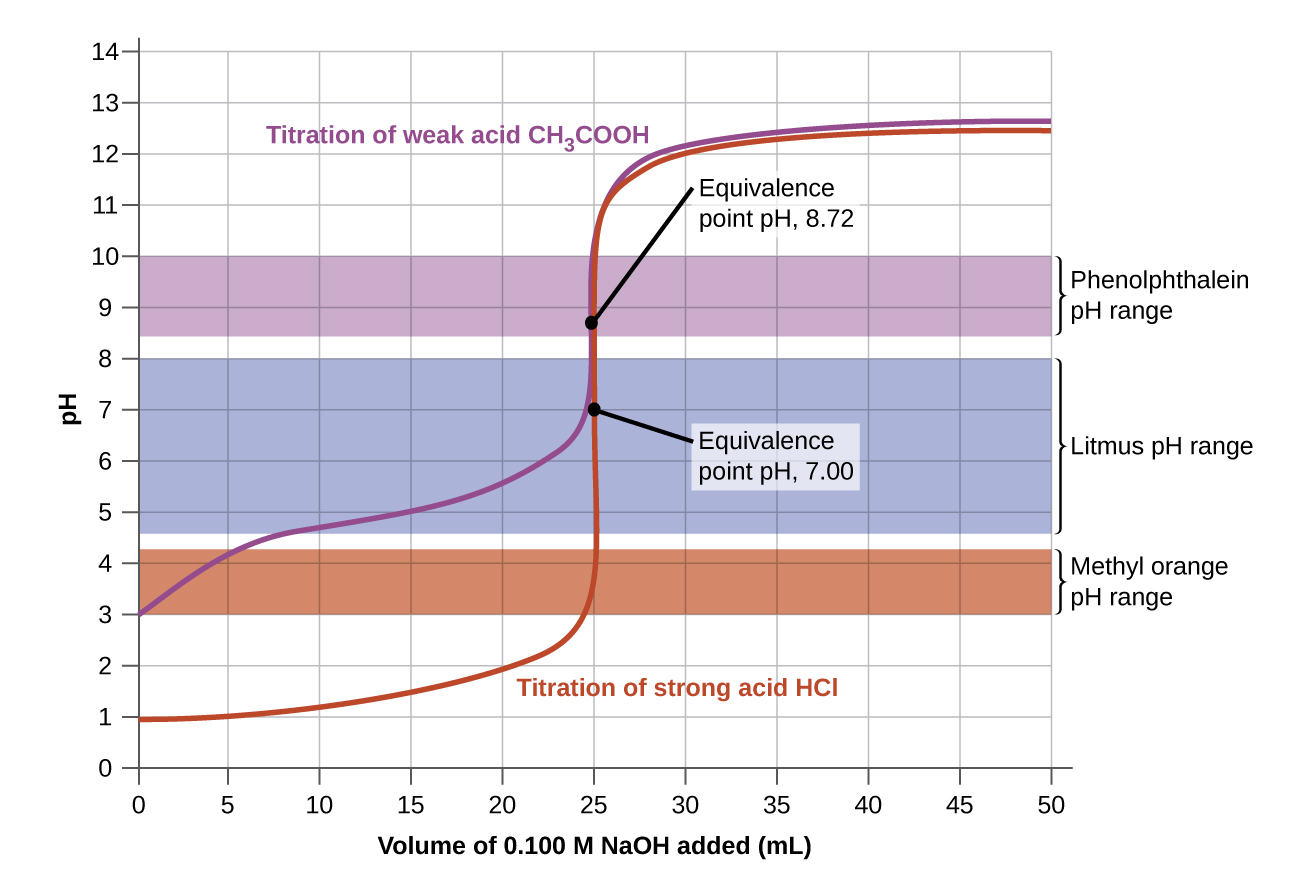
На малюнку\(\PageIndex{3}\): Графік показує криву титрування для титрування 25,00 мл 0,100 M CH ₃ CO ₂ H (слабка кислота) з 0.100 M NaOH (сильна основа) і крива титрування для титрування HCl (сильна кислота) з NaOH (сильна основа). Діапазони рН для зміни кольору фенолфталеїну, лакмусу та метилового апельсина позначаються затіненими ділянками.

Лакмус є підходящим показником для титрування HCl, оскільки його зміна кольору дужки точки еквівалентності. Однак ми не повинні використовувати лакмус для титрування CH ₃ CO ₂ H, оскільки рН знаходиться в межах інтервалу зміни кольору лакмусу, коли було додано лише близько 12 мл NaOH, і він не залишає діапазон, поки не буде додано 25 мл. Зміна кольору була б дуже поступовою, що відбувається під час додавання 13 мл NaOH, що робить лакмус марним як показник точки еквівалентності.

Ми могли б використовувати метиловий апельсин для титрування HCl, але це не дасть дуже точних результатів: (1) Він трохи завершує зміну кольору до досягнення точки еквівалентності (але дуже близько до неї, тому це не надто серйозно); (2) він змінює колір, як\(\PageIndex{2}\) показує малюнок, під час додавання майже 0,5 мл NaOH, що не настільки різке зміна кольору, як лакмус або фенолфталеїн; і (3) він переходить від жовтого до оранжевого до червоного, що робить виявлення точної кінцевої точки набагато складнішим, ніж безбарвна до рожева зміна фенолфталеїну. Малюнок\(\PageIndex{2}\) показує нам, що метиловий апельсин був би абсолютно марним як показник для титрування CH ₃ CO ₂ H. Його зміна кольору починається після додавання приблизно 1 мл NaOH і закінчується, коли було додано близько 8 мл. Зміна кольору завершується задовго до досягнення точки еквівалентності (яка виникає, коли 25,0 мл NaOH було додано) і, отже, не дає вказівки на точку еквівалентності.

Ми базуємо свій вибір індикатора на розрахунковому рН, рН в точці еквівалентності. У точці еквівалентності еквівалентні кількості кислоти та основи були змішані, і розрахунок стає рН розчину солі, отриманого в результаті титрування.

Резюме

Крива титрування - це графік, який пов'язує зміну рН кислого або основного розчину з об'ємом доданого титранту. Характеристики кривої титрування залежать від конкретних розв'язків, які титруються. РН розчину в точці еквівалентності може бути більше, рівним або менше 7,00. Вибір показника для даного титрування залежить від очікуваного рН в точці еквівалентності титрування, і діапазону зміни кольору індикатора.

Глосарій

кислотно-лужний показник: органічна кислота або основа, колір якої змінюється в залежності від рН розчину він знаходиться в

інтервал зміни кольору: діапазон pH, над яким відбувається зміна кольору індикатора

крива титрування: ділянка рН розчину кислоти або основи в порівнянні з об'ємом основи або кислоти, доданої під час титрування