13.4: Розрахунки рівноваги

Цілі навчання

• Написати рівняння, що представляють зміни концентрації та тиску для хімічних видів у рівноважних системах
• Використовуйте алгебру для виконання різних типів розрахунків рівноваги

Ми знаємо, що при рівновазі значення коефіцієнта реакції будь-якої реакції дорівнює її константі рівноваги. Таким чином, ми можемо використовувати математичний вираз для Q для визначення ряду величин, пов'язаних з реакцією при рівновазі або наближенні рівноваги. Хоча ми навчилися визначати, в якому напрямку реакція зміститься, щоб досягти рівноваги, ми хочемо розширити це розуміння на кількісні розрахунки. Ми робимо це, оцінюючи способи зміни концентрацій продуктів та реагентів у міру наближення реакції до рівноваги, маючи на увазі стехіометричні співвідношення реакції. Цей алгебраїчний підхід до розрахунків рівноваги буде досліджений у цьому розділі.

Зміни концентрацій або тиску реагентів і продуктів відбуваються, коли реакційна система наближається до рівноваги. У цьому розділі ми побачимо, що ми можемо пов'язати ці зміни один з одним, використовуючи коефіцієнти збалансованого хімічного рівняння, що описує систему. Використовуємо в якості прикладу розкладання аміаку.

При нагріванні аміак оборотно розкладається на азот і водень згідно з таким рівнянням:

\[\ce{2NH3}(g)⇌\ce{N2}(g)+\ce{3H2}(g) \nonumber \]

Якщо зразок аміаку розкладається в замкнутій системі і концентрація N ₂ збільшується на 0,11 М, зміна концентрації N ₂, Δ [N ₂], кінцевої концентрації мінус початкової концентрації, становить 0,11 М. Зміна позитивна, оскільки концентрація N ₂ збільшується.

Зміна концентрації Н ₂, Δ [H ₂], також є позитивним - концентрація Н ₂ збільшується в міру розкладання аміаку. Хімічне рівняння говорить нам, що зміна концентрації Н ₂ втричі перевищує зміну концентрації N ₂, оскільки для кожного виробленого моля N ₂ виробляється 3 молі Н ₂.

\[ \begin{align*} \ce{Δ[H2]} &=3×\ce{Δ[N2]} \\[4pt] &=3×(0.11\:M) \\[4pt] &=0.33\:M \end{align*} \nonumber \]

Зміна концентрації NH ₃, Δ [NH ₃] вдвічі більше, ніж Δ [N ₂]; рівняння вказує на те, що 2 молі NH ₃ повинні розкладатися для кожного утвореного моля N ₂. Однак зміна концентрації NH ₃ є негативним, оскільки концентрація аміаку зменшується в міру його розкладання.

\[ \begin{align*} Δ[\ce{NH3}] &=−2×Δ[\ce{N2}] \\[4pt] &=−2×(0.11\:M) \\[4pt] &=−0.22\:M \end{align*} \nonumber \]

Ми можемо співвідносити ці відносини безпосередньо з коефіцієнтами в рівнянні.

\ [\ почати {вирівняти}
&\ фантом {Δ [NH3}\ ce {2NH3} (г)

&&&\ фантом {Δ [N2}\ ce {N2} (г)

&&&&\ фантом {Δ [H2]}\ ce {3H2} (г)\\
&Δ [ce {NH3}] =−2×Δ {ce N2}] & & Δ [\ ce {N2}] =0,1\ :М & підсилювач; & Δ [\ ce {H2}] = 3 × Δ [\ ce {N2}]
\ кінець {вирівняти}\ номер\]

Зверніть увагу, що всі зміни з одного боку стрілок мають один і той же знак і що всі зміни на іншій стороні стрілок мають протилежний знак.

Якби ми не знали величини зміни концентрації N ₂, ми могли б уявити її символом x.

\(Δ[\ce{N2}]=x\)

Зміни в інших концентраціях будуть представлені у вигляді:

\(Δ[\ce{H2}]=3×Δ[\ce{N2}]=3x\)

\(Δ[\ce{NH3}]=−2×Δ[\ce{N2}]=−2x\)

Коефіцієнти в членах Δ ідентичні тим, що в збалансованому рівнянні для реакції.

\ (\ почати {вирівняти} {3}
&\ ce {2NH3} (г)\ :&&\ ce {N2} (г) +\ :&&\ ce {3H2} (г)\\
&&2x &x &3x
\ кінець {вирівняти}\)

Найпростіший для нас спосіб знайти коефіцієнти на зміни концентрації в будь-якій реакції - використовувати коефіцієнти в збалансованому хімічному рівнянні. Ознака коефіцієнта позитивний при збільшенні концентрації; він негативний при зменшенні концентрації.

Приклад\(\PageIndex{1}\): Determining Relative Changes in Concentration

Завершіть зміни концентрацій для кожної з наступних реакцій.

(а)\ (\ почати {вирівняти} {3}
&\ ce {C2H2} (г) +\ :&&\ ce {2Br2} (г)\ :&&\ ce {C2H2Br4} (г)\\
&x &&\ підкреслення {\ hspace {40px}} &&\ підкреслення {\ hspace {40px}}
\ кінець {вирівняти}\)

(b)\ (\ почати {вирівняти} {3}
&\ ce {I2} (aq) +\ :&&\ ce {I-} (aq)\ :&&\ ce {I3-} (aq)\\
&\ підкреслення {\ hspace {40px}} &&\ підкреслення {\ hspace {40px}} &X
\ кінець {вирівняти}\)

(c)\ (\ почати {вирівняти} {3}
&\ ce {C3H8} (г) +\ :&&\ ce {5O2} (г)\ :&&\ ce {3CO2} (г) +\ :&&\ ce {4H2O} (г)\\
&x &&\ підкреслення {\ hspace {40px}} &\ підкреслення {\ hspace 40px}} &&\ підкреслення {\ hspace {40px}}
\ end {вирівняти}\)

S рішення

(а)\ (\ почати {вирівняти} {3}
&\ ce {C2H2} (г) +\ :&&\ ce {2Br2} (г)\ :&&\ ce {C2H2Br4} (г)\\
&х &&&-х
\ кінець {вирівняти}\)

(b)\ (\ почати {вирівняти} {3}
&\ ce {I2} (aq) +\ :&&\ ce {I-} (aq)\ :&&\ ce {I3-} (aq)\\
&&-х &х
\ кінець {вирівняти}\)

(c)\ (\ почати {вирівняти} {3}
&\ ce {C3H8} (г) +\ :&&\ ce {5O2} (г)\ :&&\ ce {3CO2} (г) +\ :&&\ ce {4H2O} (г)\\
&х &&-3x &-4x
\ кінець {вирівняти}\

Вправа\(\PageIndex{1}\)

Завершіть зміни концентрацій для кожної з наступних реакцій:

(a)\ (\ почати {вирівняти} {3}
&\ ce {2SO2} (г) +\ :&&\ ce {O2} (г)\ :&&\ ce {2SO3} (г)\\
&\ підкреслення {\ hspace {40px}} &x &\ підкреслення {\ hspace {40px}}
\ кінець {вирівняти}\)

(b)\ (\ почати {вирівняти} {3}
&\ ce {C4H8} (г)\ :&&\ ce {2C2H4} (г)\\
&\ підкреслення {\ hspace {40px}} &&-2x
\ end {вирівняти}\)

(c)\ (\ почати {вирівняти} {3}
&\ ce {4NH3} (г) +\ :&&\ ce {7H2O} (г)\ :&&\ ce {4NO2} (г) +\ :&&\ ce {6H2O} (г)\\ &\ підкреслення {\ hspace {40px}} &\ підкреслення {\ hspace {40px}} &\ підкреслення {\ hspace {40px} px}} &\ підкреслення {\ hspace {40px}} &&\ підкреслення {\ hspace {40px}}
\ end {
вирівняти}\)

Відповідь

2 х, х, −2 х

Відповідь б

x, −2 х

Відповідь c

4 x, 7 x, −4 x, −6 x або −4 x, −7 x, 4 x, 6 x

Розрахунки за участю рівноваги

Оскільки значення коефіцієнта реакції будь-якої реакції при рівновазі дорівнює її константі рівноваги, ми можемо використовувати математичний вираз для Q _c (тобто закон масової дії) для визначення ряду величин, пов'язаних з реакцією при рівновазі. Це може допомогти, якщо мати на увазі, що Q _c = K _c (при рівновазі) у всіх цих ситуаціях і що існує лише три основні типи розрахунків:

1. Розрахунок постійної рівноваги. Якщо відомі концентрації реагентів і продуктів при рівновазі, можна розрахувати значення константи рівноваги для реакції.
2. Розрахунок відсутніх рівноважних концентрацій. Якщо відомо значення постійної рівноваги і всіх рівноважних концентрацій, крім однієї, можна розрахувати решту концентрації.
3. Розрахунок рівноважних концентрацій від початкових концентрацій. Якщо відомо значення константи рівноваги і сукупність концентрацій реагентів і продуктів, які не знаходяться в рівновазі, можна розрахувати концентрації при рівновазі.

Подібний список може бути сформований за допомогою Q _P, K _P та парціального тиску. Ми розглянемо вирішення кожного з цих випадків послідовно.

Розрахунок постійної рівноваги

Оскільки закон масової дії є єдиним рівнянням, яке ми повинні описати взаємозв'язок між K _c і концентраціями реагентів і продуктів, будь-яка проблема, яка вимагає від нас вирішення для K _c, повинна надавати достатньо інформації для визначення реагенту і концентрації продукту при рівновазі. Озброївшись концентраціями, ми можемо вирішити рівняння для K _c, оскільки воно буде єдиним невідомим.

Приклад\(\PageIndex{1}\) показав нам, як визначити константу рівноваги реакції, якщо ми знаємо концентрації реагентів і продуктів в рівновазі. Наступний приклад показує, як використовувати стехіометрію реакції і комбінацію початкових концентрацій і рівноважних концентрацій для визначення константи рівноваги. Ця методика, яка зазвичай називається таблицею ICE - для I початкового, C change, і E рівноваги - буде корисним у вирішенні багатьох проблем рівноваги. Діаграма генерується, починаючи з відповідної реакції рівноваги. Під реакцією перераховані початкові концентрації реагентів та продуктів - ці умови, як правило, передбачені в проблемі, і ми вважаємо, що не відбулося зсуву до рівноваги. Наступним рядком даних є зміна, яка відбувається, коли система зміщується в бік рівноваги—не забудьте розглянути стехіометрію реакції, як описано в попередньому розділі цієї глави. Останній рядок містить концентрації після досягнення рівноваги.

Приклад\(\PageIndex{2}\): Calculation of an Equilibrium Constant

Молекули йоду оборотно реагують з йодидними іонами, утворюючи іони трийодидів.

\[\ce{I2}(aq)+\ce{I-}(aq)⇌\ce{I3-}(aq) \nonumber \]

Якщо розчин з концентраціями I ₂ і I ⁻ обидва рівні 1,000 × 10 ⁻³ М перед реакцією дає рівноважну концентрацію I ₂ 6,61 × 10 ⁻⁴ М, яка постійна рівноваги для реакції?

Рішення

Ми почнемо цю задачу з розрахунку змін концентрації в міру переходу системи до рівноваги. Потім визначаємо рівноважні концентрації і, нарешті, постійну рівноваги. Спочатку ми створили таблицю з початковими концентраціями, змінами концентрацій та рівноважними концентраціями, використовуючи − x як зміну концентрації I ₂.

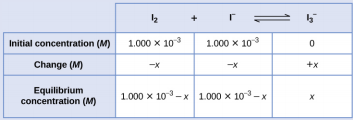
Оскільки задана рівноважна концентрація I ₂, ми можемо вирішити для х. При рівновазі концентрація I ₂ дорівнює 6,61 × 10 ⁻⁴ М так, щоб

\(1.000×10^{−3}−x=6.61×10^{−4}\)

\(x=1.000×10^{−3}−6.61×10^{−4}\)

\(=3.39×10^{−4}\:M\)

Тепер ми можемо заповнити таблицю з концентраціями при рівновазі.

Тепер обчислимо значення константи рівноваги.

\(K_c=Q_c=\ce{\dfrac{[I3- ]}{[I2][I- ]}}\)

\(=\dfrac{3.39×10^{−4}\:M}{(6.61×10^{−4}\:M)(6.61×10^{−4}\:M)}=776\)

Вправа\(\PageIndex{2}\)

Етанол та оцтова кислота реагують і утворюють воду та етилацетат, розчинник, відповідальний за запах деяких засобів для зняття лаку.

\(\ce{C2H5OH + CH3CO2H ⇌ CH3CO2C2H5 + H2O}\)

Коли 1 моль кожного з С ₂ Н ₅ ОН і СН ₃ СО _{2 Н 2} Н дають вступати в реакцію в 1 л розчинника діоксану, рівновага встановлюється, коли залишається\(\dfrac{1}{3}\) моль кожного з реагентів. Обчисліть постійну рівноваги для реакції. (Примітка: Вода не є розчинником у цій реакції.)

Відповідь

_{К с} = 4

Розрахунок відсутньої рівноважної концентрації

Якщо ми знаємо постійну рівноваги для реакції і знаємо концентрації при рівновазі всіх реагентів і продуктів, крім одного, ми можемо обчислити відсутню концентрацію.

Приклад\(\PageIndex{3}\): Calculation of a Missing Equilibrium Concentration

Оксиди азоту - забруднювачі повітря, що утворюються в результаті реакції азоту і кисню при високих температурах. При 2000° С, значення константи рівноваги для реакції\(\ce{N2}(g)+\ce{O2}(g)⇌\ce{2NO}(g)\), становить 4,1 × 10 ⁻⁴. Знайти концентрацію NO (g) в рівноважної суміші з повітрям при тиску 1 атм при цій температурі. На повітрі [N ₂] = 0,036 моль/л і [O ₂] 0,0089 моль/л.

Рішення

Нам дано всі рівноважні концентрації, крім концентрації NO. Таким чином, ми можемо вирішити для відсутньої рівноважної концентрації шляхом перестановки рівняння для константи рівноваги.

\(K_c=Q_c=\ce{\dfrac{[NO]^2}{[N2][O2]}}\)

\(\ce{[NO]^2}=K_c\ce{[N2][O2]}\)

\(\ce{[NO]}=\sqrt{K_c\ce{[N2][O2]}}\)

\(=\sqrt{(4.1×10^{−4})(0.036)(0.0089)}\)

\(=\sqrt{1.31×10^{−7}}\)

\(=3.6×10^{−4}\)

Таким чином, [NO] становить 3,6 × 10 ⁻⁴ моль/л при рівновазі в цих умовах.

Ми можемо перевірити нашу відповідь, підставивши всі концентрації рівноваги у вираз для коефіцієнта реакції, щоб побачити, чи дорівнює він постійній рівноваги.

\[ \begin{align*} Q_c=\ce{\dfrac{[NO]^2}{[N2][O2]}} \\[4pt] &=\dfrac{(3.6×10^{−4})^2}{(0.036)(0.0089)} \\[4pt] &=4.0×10^{−4}=K_c \end{align*} \nonumber \]

Відповідь перевіряє; наше обчислене значення дає константу рівноваги в межах похибки, пов'язаної зі значними цифрами в задачі.

Вправа\(\PageIndex{3}\)

Константа рівноваги для реакції азоту і водню з отриманням аміаку при певній температурі становить 6,00 × 10 ⁻². Обчисліть рівноважну концентрацію аміаку, якщо рівноважні концентрації азоту і водню складають 4,26 М і 2,09 М відповідно.

Відповідь

1,53 моль/л

Розрахунок змін концентрації

Якщо ми знаємо постійну рівноваги для реакції і набір концентрацій реагентів і продуктів, які не знаходяться в рівновазі, ми можемо обчислити зміни концентрацій у міру досягнення системи рівноваги, а також нові концентрації при рівновазі. Типову процедуру можна узагальнити в чотири етапи.

1. Визначте напрямок, в якому протікає реакція, щоб прийти до рівноваги.
   • Напишіть збалансоване хімічне рівняння для реакції.
   • Якщо напрямок, в якому повинна протікати реакція для досягнення рівноваги, не очевидний, обчисліть Q _c з початкових концентрацій і порівняти з K _c, щоб визначити напрямок зміни.
2. Визначте відносні зміни, необхідні для досягнення рівноваги, потім запишіть концентрації рівноваги з точки зору цих змін.
   • Визначте зміни початкових концентрацій, які необхідні для того, щоб реакція досягла рівноваги. Як правило, ми представляємо найменшу зміну символом x і виражаємо інші зміни з точки зору найменшої зміни.
   • Визначте відсутні рівноважні концентрації з точки зору початкових концентрацій та змін концентрації, визначених у (а).
3. Вирішити для зміни і рівноваги концентрації.
   • Підставте концентрації рівноваги у вираз для константи рівноваги, вирішіть для x та перевірте будь-які припущення, які використовуються для пошуку x.
   • Обчисліть рівноважні концентрації.
4. Перевірте арифметику.
   • Перевірте розраховані концентрації рівноваги, підставивши їх у вираз рівноваги і визначивши, чи дають вони постійну рівноваги.

Іноді певний крок може відрізнятися від проблеми до проблеми - він може бути більш складним у деяких проблемах і менш складним в інших. Однак кожен розрахунок рівноважних концентрацій з набору початкових концентрацій буде включати ці кроки.

При вирішенні задач рівноваги, які передбачають зміни концентрації, іноді зручно налаштувати таблицю ДВС, як описано в попередньому розділі.

Приклад\(\PageIndex{4}\): Calculation of Concentration as a Reaction Equilibrates

При певних умовах константа рівноваги для розкладання pCl ₅ (g) на pCl ₃ (g) і Cl ₂ (g) становить 0,0211. Які рівноважні концентрації pCl ₅, pCl ₃ і Cl ₂, якщо початкова концентрація pCl ₅ становила 1,00 М?

Рішення

Скористайтеся покроковим процесом, описаним раніше.

1. Збалансоване рівняння для розкладання pCl ₅ дорівнює
   \(\ce{PCl5}(g)⇌\ce{PCl3}(g)+\ce{Cl2}(g)\)

Оскільки у нас немає продуктів спочатку, Q _c = 0 і реакція буде протікати вправо.

• Уявімо збільшення концентрації pCl ₃ символом х. Інші зміни можуть бути записані через x, враховуючи коефіцієнти в хімічному рівнянні.
  \ (\ почати {вирівняти} {3}
  &\ ce {pCl5} (г)\ :&&\ ce {pCl3} (г) +\ :&&\ ce {Cl2} (г)\\
  &&-х &х
  \ кінець {вирівняти}\)

• Зміни концентрації та вирази для рівноважних концентрацій:

   

  

  Ця таблиця складається з двох основних стовпців і чотирьох рядків. Перший рядок для першого стовпця не має заголовка, а потім має наступне в першому стовпці: Початкова концентрація (M), Зміна (M), Рівноважна концентрація (M). Другий стовпець має заголовок «P C l індекс 5 рівноважна стрілка P C l індекс 3 плюс C l індекс 2.» Під другим стовпцем знаходиться підгрупа з трьох рядків і трьох стовпців. Перший стовпець має такі параметри: 1,00, від'ємний x, 1,00 мінус x. Другий стовпець має такі значення: 0, позитивний x, 0 плюс x дорівнює x. Третій стовпець має такі значення: 0, позитивний x, 0 плюс x дорівнює x.

• Підстановка рівноважних концентрацій на рівняння рівноваги дає
  \(K_c=\ce{\dfrac{[PCl3][Cl2]}{[PCl5]}}=0.0211\)
  \(=\dfrac{(x)(x)}{(1.00−x)}\)

  Це рівняння містить тільки одну змінну, x, зміна концентрації. Ми можемо записати рівняння як квадратне рівняння і вирішити для x за допомогою квадратичної формули.

  \(0.0211=\dfrac{(x)(x)}{(1.00−x)}\)
  \(0.0211(1.00−x)=x^2\)
  \(x^2+0.0211x−0.0211=0\)

  Рівняння виду ax ² + bx + c = 0 можна переставити для розв'язання для x:

  \(x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}\)

  У цьому випадку a = 1, b = 0,0211, а c = −0,0211. Підстановка відповідних значень для a, b і c дає:

  \(x=\dfrac{−0.0211±\sqrt{(0.0211)^2−4(1)(−0.0211)}}{2(1)}\)
  \(=\dfrac{−0.0211±\sqrt{(4.45×10^{−4})+(8.44×10^{−2})}}{2}\)
  \(=\dfrac{−0.0211±0.291}{2}\)

  Звідси

  \(x=\dfrac{−0.0211+0.291}{2}=0.135\)

  або

  \(x=\dfrac{−0.0211−0.291}{2}=−0.156\)

  Квадратні рівняння часто мають два різних рішення, одне фізично можливо і інше, яке фізично неможливо (сторонній корінь). У цьому випадку друге рішення (−0,156) фізично неможливо, оскільки ми знаємо, що зміна повинна бути позитивним числом (інакше ми отримаємо негативні значення для концентрацій продуктів). Таким чином, х = 0,135 М.

  Рівноважні концентрації

  \(\ce{[PCl5]}=1.00−0.135=0.87\:M\)
  \(\ce{[PCl3]}=x=0.135\:M\)
  \(\ce{[Cl2]}=x=0.135\:M\)
• Підстановка у вираз для K _c (для перевірки обчислення) дає
  \(K_c=\ce{\dfrac{[PCl3][Cl2]}{[PCl5]}}=\dfrac{(0.135)(0.135)}{0.87}=0.021\)

  Константа рівноваги, розрахована з рівноважних концентрацій, дорівнює значенню K _c, заданому в задачі (при округленні до належної кількості значущих цифр). Таким чином, розрахункові концентрації рівноваги перевіряють.

Вправа\(\PageIndex{4A}\)

Оцтова кислота, СН ₃ СО ₂ Н, вступає в реакцію з етанолом, C ₂ H ₅ OH, з утворенням води і етилацетату, CH ₃ CO _{2 C 2} H ₅.

\[\ce{CH3CO2H + C2H5OH ⇌ CH3CO2C2H5 + H2O} \nonumber \]

Константа рівноваги для цієї реакції з діоксаном як розчинником дорівнює 4,0. Які рівноважні концентрації при отриманні суміші, яка становить 0,15 М в СН ₃ СО ₂ Н, 0,15 М в С ₂ Н ₅ ОН, 0,40 М в СН ₃, СО _{2 С 2} Н ₅, і 0,40 М в Н ₂ O змішують в достатній кількості діоксану, щоб зробити 1,0 л розчину?

Відповідь

[СН ₃ СО ₂ Н] = 0,36 М, [С ₂ Н ₅ ОН] = 0,36 М, [СН ₃ СО ₂ С ₂ Н ₅] = 0,17 М, [Н ₂ О] = 0,17 М

Вправа\(\PageIndex{4B}\)

Колба об'ємом 1,00 л заповнюється 1,00 молями Н ₂ і 2,00 молями I ₂. Значення константи рівноваги для реакції водню і йоду, що реагують з утворенням йодистого водню, становить 50,5 при заданих умовах. Які рівноважні концентрації Н ₂, I ₂ і HI в моль/л?

\[\ce{H2}(g)+\ce{I2}(g)\rightleftharpoons\ce{2HI}(g) \nonumber \]

Відповідь

[Н ₂] = 0,06 М, [Я ₂] = 1,06 М, [ПРИВІТ] = 1,88 М

Іноді можна використовувати хімічне розуміння для пошуку рішень задач рівноваги, фактично не вирішуючи квадратичного (або більш складного) рівняння. По-перше, однак, корисно перевірити, що рівновага може бути отримана, починаючи з двох крайнощів: всіх (або в основному) реагентів і всіх (або в основному) продуктів.

Розглянемо іонізацію 0,150 М ГА, слабку кислоту.

\(\ce{HA}(aq)⇌\ce{H+}(aq)+\ce{A-}(aq) \hspace{20px} K_c=6.80×10^{−4}\)

Найбільш очевидним способом визначення рівноважних концентрацій було б почати тільки з реагентів. Це можна було б назвати відправною точкою «всіх реагентів». Використовуючи x для кількості кислоти, іонізованої при рівновазі, це таблиця ДВС і розчин.

 

Ця таблиця складається з двох основних стовпців і чотирьох рядків. Перший рядок для першого стовпця не має заголовка, а потім має наступне: Початковий тиск (M), Зміна (M), Рівновага (M). Другий стовпець має заголовок: «H A (a q) рівноважна стрілка H верхній індекс плюс (a q) плюс A нижній негативний знак (a q)». Під другим стовпцем знаходиться підгрупа з трьох стовпців і трьох рядків. Перший стовпець має такі значення: 0,150, від'ємний x, 0,150 мінус x. Другий стовпець має такі значення: 0, x, x. Третій стовпець має такі значення: 0, x, x.

Налаштування та розв'язування квадратного рівняння дає

\(K_c=\ce{\dfrac{[H+][A- ]}{[HA]}}=\dfrac{(x)(x)}{(0.150−x)}=6.80×10^{−4}\)

\(x^2+6.80×10^{−4}x−1.02×10^{−4}=0\)

\(x={−6.80×10^{−4}±\sqrt{(6.80×10^{−4})^2−(4)(1)(−1.02×10^{−4})}}{(2)(1)}\)

\(x=0.00977\:M\textrm{ or }−0.0104\:M\)

Використовуючи позитивний (фізичний) корінь, концентрації рівноваги

\(\ce{[HA]}=0.150−x=0.140\:M\)

\(\ce{[H+]}=\ce{[A- ]}=x=0.00977\:M\)

Менш очевидним способом вирішення проблеми було б припустити, що спочатку всі ГК іонізуються, потім система приходить до рівноваги. Це можна було б назвати відправною точкою «весь продукт». Припускаючи, що всі ГК іонізує дає

\(\ce{[HA]}=0.150−0.150=0\:M\)

\(\ce{[H+]}=0+0.150=0.150\:M\)

\(\ce{[A- ]}=0+0.150=0.150\:M\)

Використовуючи їх як початкові концентрації та «y» для представлення концентрації ГК при рівновазі, це таблиця ICE для цієї відправної точки.

 

Ця таблиця складається з двох основних стовпців і чотирьох рядків. Перший рядок для першого стовпця не має заголовка, а потім має наступне: Початковий тиск (M), Зміна (M), Рівновага (M). Другий стовпець має заголовок: «H A (a q) рівноважна стрілка H верхній індекс плюс (a q) плюс A нижній негативний знак (a q)». Під другим стовпцем знаходиться підгрупа з трьох стовпців і трьох рядків. Перший стовпець має такі значення: 0, додатне y, y. Другий стовпець має такі значення: 0,150, від'ємний y, 0,150 мінус y. Третій стовпець має такі значення: 0,150, від'ємний y та 0,150 мінус y.

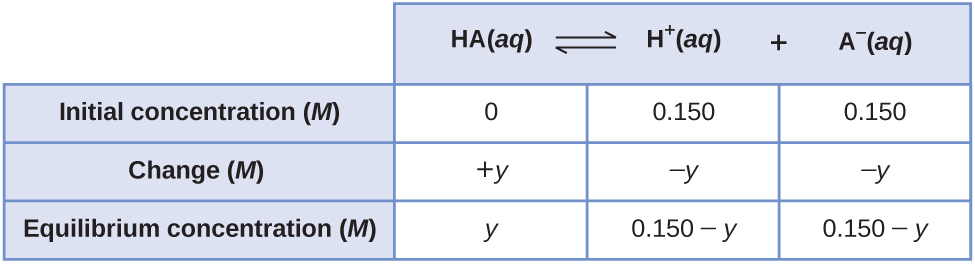
Налаштування та розв'язування квадратного рівняння дає

\(K_c=\ce{\dfrac{[H+][A- ]}{[HA]}}=\dfrac{(0.150−y)(0.150−y)}{(y)}=6.80×10^{−4}\)

\(6.80×10^{−4}y=0.0225−0.300y+y^2\)

Зберігайте кілька додаткових значущих цифр, щоб мінімізувати проблеми з округленням.

\(y^2−0.30068y+0.022500=0\)

\(y=\dfrac{0.30068±\sqrt{(0.30068)^2−(4)(1)(0.022500)}}{(2)(1)}\)

\(y=\dfrac{0.30068±0.020210}{2}\)

Округлення кожного рішення до трьох значущих цифр дає

\(y=0.160\:M\textrm{ or }y=0.140\:M\)

Використання фізично значущого кореня (0,140 М) дає рівноважні концентрації як

\(\ce{[HA]}=y=0.140\:M\)

\(\ce{[H+]}=0.150−y=0.010\:M\)

\(\ce{[A- ]}=0.150−y=0.010\:M\)

Таким чином, два підходи дають однакові результати (до трьох знаків після коми), і показують, що обидві початкові точки ведуть до однакових умов рівноваги. Початкова точка «всіх реагентів» призвела до відносно невеликої зміни (x), оскільки система була близькою до рівноваги, тоді як вихідна точка «весь продукт» мала відносно велику зміну (y), яка була майже розміром початкових концентрацій. Можна сказати, що система, яка починає «близько» до рівноваги, зажадає лише «невеликої» зміни умов (х) для досягнення рівноваги.

Нагадаємо, що малий K _c означає, що дуже мало реагентів утворюють продукти, а великий K _c означає, що більшість реагентів утворюють продукти. Якщо система може бути влаштована так, що вона починає «близько» до рівноваги, то якщо зміна (х) невелика в порівнянні з будь-якими початковими концентраціями, нею можна знехтувати. Малий зазвичай визначається як результат помилки менше 5%. Наступні два приклади демонструють це.

Приклад\(\PageIndex{5}\): Approximate Solution Starting Close to Equilibrium

Які концентрації при рівновазі 0,15 М розчину HCN?

\[\ce{HCN}(aq)⇌\ce{H+}(aq)+\ce{CN-}(aq) \hspace{20px} K_c=4.9×10^{−10} \nonumber \]

Рішення в

Використання «x» для представлення концентрації кожного продукту в рівновазі дає цю таблицю ICE.

 

Ця таблиця складається з двох основних стовпців і чотирьох рядків. Перший рядок для першого стовпця не має заголовка, а потім має наступне: Початковий тиск (M), Зміна (M), Рівновага (M). Другий стовпець має заголовок: «H C N (a q) рівноважна стрілка H верхній індекс плюс (a q) плюс C N підрядковий негативний знак (a q)». Під другим стовпцем знаходиться підгрупа з трьох стовпців і трьох рядків. Перший стовпець має такі значення: 0,15, від'ємний x, 0,15 мінус x. Другий стовпець має такі значення: 0, x, x. Третій стовпець має такі значення: 0, x, x.

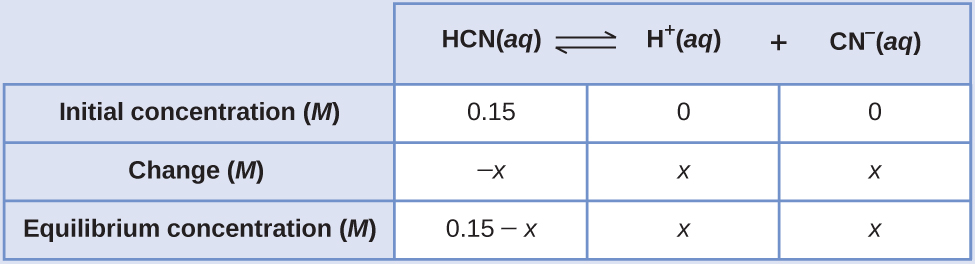
Точне рішення може бути отримано за допомогою квадратичної формули з

\[K_c=\dfrac{(x)(x)}{0.15−x} \nonumber \]

вирішення

\[x^2+4.9×10^{−10}−7.35×10^{−11}=0 \nonumber \]

\[x=8.56×10^{−6}\:M\textrm{ (3 sig. figs.)}=8.6×10^{−6}\:M\textrm{ (2 sig. figs.)} \nonumber \]

Таким чином [Н ⁺] = [СН ^—] = х = 8,6 × 10 ^—6 М і [HCN] = 0,15 - х = 0,15 М.

В цьому випадку хімічна інтуїція може забезпечити більш просте рішення. Від постійної рівноваги і початкових умов х повинен бути малим в порівнянні з 0,15 М. Більш формально, якщо\(x≪0.15\), то 0,15 — х ≈ 0,15. Якщо це припущення вірно, то воно спрощує отримання х

\[K_c=\dfrac{(x)(x)}{0.15−x}≈\dfrac{x^2}{0.15} \nonumber \]

\[4.9×10^{−10}=\dfrac{x^2}{0.15} \nonumber \]

\[x^2=(0.15)(4.9×10^{−10})=7.4×10^{−11} \nonumber \]

\[x=\sqrt{7.4×10^{−11}}=8.6×10^{−6}\:M \nonumber \]

У цьому прикладі рішення точного (квадратичного) рівняння і використання наближень дало однаковий результат двом значущим фігурам. Хоча більшу частину часу наближення трохи відрізняється від точного рішення, якщо похибка менше 5%, приблизне рішення вважається дійсним. У цій задачі 5% застосовується до ПЧ (0,15 — х) ≈ 0,15 М, тому якщо

\[\dfrac{x}{0.15}×100\%=\dfrac{8.6×10^{−6}}{0.15}×100\%=0.006\% \nonumber \]

становить менше 5%, як і в даному випадку, припущення є дійсним. Таким чином, приблизне рішення є дійсним рішенням.

Вправа\(\PageIndex{5}\)

Які рівноважні концентрації в розчині 0,25 М NH ₃?

\(\ce{NH3}(aq)+\ce{H2O}(l)⇌\ce{NH4+}(aq)+\ce{OH-}(aq) \hspace{20px} K_c=1.8×10^{−5}\)

Припустимо, що х набагато менше 0,25 М і обчислити похибку в своєму припущенні.

Відповідь

\(\ce{[OH- ]}=\ce{[NH4+]}=0.0021\:M\); [NH ₃] = 0,25 М, похибка = 0,84%

Другий приклад вимагає, щоб вихідна інформація була трохи оброблена, але її все одно можна вирішити за допомогою невеликого наближення x.

Приклад\(\PageIndex{6}\): Approximate Solution After Shifting Starting Concentration

Іони міді (II) утворюють комплексний іон в присутності аміаку

\[\ce{Cu^2+}(aq)+\ce{4NH3}(aq)⇌\ce{Cu(NH3)4^2+}(aq) \hspace{20px} K_c=5.0×10^{13}=\ce{\dfrac{[Cu(NH3)4^2+]}{[Cu^2+(aq)][NH3]^4}} \nonumber \]

Якщо 0,010 моль Cu ^{2 +} додають до 1,00 л розчину, що становить 1,00 М NH ₃, які концентрації, коли система приходить до рівноваги?

Розчин. Початкова концентрація міді (II) становить 0,010 М. Константа рівноваги дуже велика, тому краще було б почати з якомога більшої кількості продукту, оскільки «всі продукти» набагато ближче до рівноваги, ніж «всі реагенти». Зверніть увагу, що Cu ^{2 +} є граничним реагентом; якщо всі 0,010 М його реагують на формування продукту, концентрації будуть

\[\ce{[Cu^2+]}=0.010−0.010=0\:M \nonumber \]

\[\ce{[Cu(NH3)4^2+]}=0.010\:M \nonumber \]

\[\ce{[NH3]}=1.00−4×0.010=0.96\:M \nonumber \]

Використання цих «зрушених» значень як початкових концентрацій з x як концентрація вільних іонів міді (II) при рівновазі дає цю таблицю ДВС.

 

Ця таблиця складається з двох основних стовпців і чотирьох рядків. Перший рядок для першого стовпця не має заголовка, а потім має наступне: Початковий тиск (M), Зміна (M), Рівновага (M). Другий стовпець має заголовок: «C u верхній індекс 2 позитивний знак (a q) плюс 4 N H індекс 3 (a q) рівноважна стрілка C u (N H індекс 3) підстроковий 4 верхній індекс 2 позитивний знак (a q).» Під другим стовпцем знаходиться підгрупа з трьох стовпців і трьох рядків. Перший стовпець має такі значення: 0, додатне x, x. Другий стовпець має такі значення: 0,96, позитивний 4 х, 0,96 плюс 4 х. Третій стовпець має такі значення: 0,010, від'ємний x, 0,010 мінус x.

Оскільки ми починаємо близько до рівноваги, х повинен бути малим, щоб

\(0.96+4x≈0.96\:M\)

\(0.010−x≈0.010\:M\)

\(K_c=\dfrac{(0.010−x)}{x(0.96−4x)^4}≈\dfrac{(0.010)}{x(0.96)^4}=5.0×10^{13}\)

\(x=\dfrac{(0.010)}{K_c(0.96)^4}=2.4×10^{−16}\:M\)

Виберіть найменшу концентрацію для правила 5%.

\(\dfrac{2.4×10^{−16}}{0.010}×100\%=2×10^{−12}\%\)

Це набагато менше 5%, тому припущення дійсні. Концентрації при рівновазі

\(\ce{[Cu^2+]}=x=2.4×10^{−16}\:M\)

\(\ce{[NH3]}=0.96−4x=0.96\:M\)

\(\ce{[Cu(NH3)4^2+]}=0.010−x=0.010\:M\)

Починаючи з максимальної кількості продукту, ця система була близькою до рівноваги, а зміна (х) була дуже маленькою. З лише невеликою зміною, необхідною для досягнення рівноваги, рівняння для x було значно спрощено і дало дійсний результат добре в межах максимальної похибки 5%.

Вправа\(\PageIndex{6}\)

Які рівноважні концентрації при додаванні 0,25 моль Ni ^{2 +} до 1,00 л 2,00 М розчину NH ₃?

\[\ce{Ni^2+}(aq)+\ce{6NH3}(aq)⇌\ce{Ni(NH3)6^2+}(aq) \nonumber \]

с\(K_c=5.5×10^8\).

При такій великій постійній рівноваги спочатку формують якомога більше продукту, потім припускають, що лише невелика кількість (х) вироби зміщується вліво. Обчисліть похибку в своєму припущенні.

Відповідь

\(\ce{[Ni(NH3)6^2+]}=0.25\:M\), [NH ₃] = 0,50 М, [Ni ^{2 +}] = 2,9 × 10 ^—8 М, похибка = 1,2 × 10 ^—5%

Резюме

Співвідношення швидкості зміни концентрацій реакції рівні співвідношенням коефіцієнтів в збалансованому хімічному рівнянні. Ознака коефіцієнта Х позитивний при збільшенні концентрації і негативний при її зменшенні. Ми навчилися підходити до трьох основних типів задач рівноваги. Коли задано концентрації реагентів та продуктів в рівновазі, ми можемо вирішити для постійної рівноваги; коли задано постійну рівноваги та деякі концентрації, що беруть участь, ми можемо вирішити для відсутніх концентрацій; і коли задано постійну рівновагу та початкові концентрації, ми можемо вирішити для концентрацій в рівновазі.