Основні математики
- Page ID
- 22612
Експоненціальна арифметика
Експоненціальне позначення використовується для вираження дуже великих і дуже малих чисел як добуток двох чисел. Перше число твору, термін цифри, зазвичай є числом не менше 1 і не більше 10. Друге число добутку, експоненціальний термін, записується як 10 з показником. Деякі приклади експоненціальних позначень:
\ [\ почати {вирівнювати*}
1000&=1 × 10^3\\
100&= 1 × 10 ^ 2\\
10&=1 × 10^1\ 1
& = 1×10^0\
0,1 &=1×10^ {−1}\\
0,001&=1 × 10^ {−3}\\
2386 &=2.386×1000=2.38610×3\\
0.123&=1,23 × 0,1 = 1,23 × 10^ { −1}
\ end {align*}\ nonumber\]
Потужність (показник) 10 дорівнює кількості розрядів, котрі зсувається, щоб дати цифрове число. Експоненціальний метод є особливо корисним позначенням для кожного великого і дуже малого числа. Наприклад, 1 230 000 000 = 1,23 × 10 9, і 0,00000000036 = 3,6 × 10 −10.
Додавання експоненціальних чисел
Перетворіть всі числа в однакову ступінь 10, додайте цифри термінів чисел і, якщо це доречно, перетворіть термін цифри назад в число між 1 і 10, регулюючи експоненціальний член.
Додайте 5,00 × 10 −5 і 3,00 × 10 −3.
Рішення в
\ [\ почати {вирівнювати*}
3,00×10^ {−3} &=300×10^ {−5}\
(5.00×10^ {−5}) + (300 × 10^ {−5}) &=305×10^ {−5} =3.05×10^ {−3}
\ кінець {вирівнювати*}\ nonumber\]
Віднімання експоненціальних
Перетворіть всі числа в однакову ступінь 10, візьміть різницю цифр термінів і, якщо доречно, перетворіть термін цифри назад в число між 1 і 10, регулюючи експоненціальний термін.
Відніміть 4,0 × 10 −7 з 5,0 × 10 −6.
Рішення в
\ [4.0×10^ {−7} =0,40 × 10^ {−6}\
(5.0×10^ {−6}) − (0,40×10^ {−6}) =4,6×10^ {−6}\ nonumber\]
Множення експоненціальних
Помножте цифри звичайним способом і складіть показники експоненціальних членів.
Помножте 4,2 × 10 −8 на 2,0 × 10 3.
Рішення в
\[(4.2×10^{−8})×(2.0×10^3)=(4.2×2.0)×10^{(−8)+(+3)}=8.4×10^{−5} \nonumber \]
Розподіл експоненціальних чисел
Розділіть розрядний член чисельника на розрядний член знаменника і відніміть показники експоненціальних членів.
Розділіть 3,6 × 10 5 на 6,0 × 10 −4.
Рішення в
\[\dfrac{3.6×10^{−5}}{6.0×10^{−4}}=\left(\dfrac{3.6}{6.0}\right)×10^{(−5)−(−4)}=0.60×10^{−1}=6.0×10^{−2} \nonumber \]
Квадратування експоненціальних
Квадратуйте розрядний член звичайним способом і помножте показник експоненціального члена на 2.
Квадрат числа 4,0 × 10 −6.
Рішення в
\[(4.0×10^{−6})^2=4×4×10^{2×(−6)}=16×10^{−12}=1.6×10^{−11} \nonumber \]
Кубірування експоненціальних чисел
Кубик числового члена звичайним способом і помножте показник експоненціального члена на 3.
Куб цифра 2 × 10 4.
Рішення в
\[(2×10^4)^3=2×2×2×10^{3×4}=8×10^{12} \nonumber \]
Беручи квадратні корені експоненціальних чисел
При необхідності зменшіть або збільште експоненціальний термін так, щоб потужність 10 рівномірно ділилася на 2. Витягніть квадратний корінь цифрового члена і розділіть експоненціальний член на 2.
Знайти квадратний корінь розміром 1,6 × 10 −7.
Рішення в
\ [\ почати {вирівнювати*}
1,6 × 10^ {−7} &=16×10^ {−8}\
\ sqrt {16×10^ {−8}} =\ sqrt {16} ×\ sqrt {10^ {−8}} &=\ sqrt {16} ×10^ {−\ великий {\ frac {8} {2}}} =4.0×10^ {−4}
\ end {align*}\ nonumber\]
Значні цифри
Бджоляр повідомляє, що у нього 525 341 бджіл. Останні три цифри числа явно неточні, бо за час, коли зберігач підраховував бджіл, деякі з них загинули, а інші вилупилися; це досить ускладнює визначення точної кількості бджіл. Точніше було б, якби бджоляр повідомив число 525 000. Іншими словами, останні три цифри не є значними, хіба що задати позицію десяткової крапки. Їх точні значення не мають корисного в даній ситуації сенсу. Повідомляючи будь-яку інформацію як цифри, використовуйте лише стільки значущих цифр, скільки гарантує точність вимірювання.
Важливість значущих цифр полягає в їх застосуванні до фундаментальних обчислень. Крім того, сума або віднімання, сума або різниця повинні містити стільки цифр праворуч від десяткового числа, скільки в найменшому з чисел, використовуваних при обчисленні (зазначено підкресленням у наступному прикладі).
Додати 4,383 г і 0,0023 г.
Рішення в
\ [\ begin {align*}
&\ mathrm {4.38\ підкреслення {3}\ :g}\\
&\ mathrm {\\ підкреслення {0.002\ підкреслення {3}\ :g}}\\
&\ mathrm {4.38\ підкреслення {5}\ :g}
\ end {align*}\ nonumber\]
При множенні і діленні добуток або частка повинні містити не більше цифр, ніж у коефіцієнті, що містить найменшу кількість значущих цифр.
Помножте 0,6238 на 6,6.
Рішення в
\[0.623\underline{8}×6.\underline{6}=4.\underline{1} \nonumber \]
При округленні чисел збільште збережену цифру на 1, якщо за нею слідує число більше 5 («округлити вгору»). Не змінюйте збережену цифру, якщо наступні цифри менше 5 («округлити вниз»). Якщо за збереженою цифрою слідує 5, округляйте вгору, якщо збережена цифра непарна, або округляйте вниз, якщо вона парна (після округлення збережена цифра, таким чином, завжди буде парною).
Використання логарифмів та експоненціальних чисел
Загальний логарифм числа (log) - це ступінь, до якої 10 потрібно підняти, щоб дорівнювати цьому числу. Наприклад, загальний логарифм 100 дорівнює 2, тому що 10 потрібно підняти на другу ступінь, рівну 100. Далі наступні додаткові приклади.
| Число | Число, виражене експоненціально | Загальний логарифм |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 −1 | −1 |
| 0,001 | 10 −3 | −3 |
Що таке загальний логарифм 60? Оскільки 60 лежить між 10 і 100, які мають логарифми 1 і 2 відповідно логарифм 60 дорівнює 1.7782; тобто,
\[60=10^{1.7782} \nonumber \]
Загальний логарифм числа менше 1 має від'ємне значення. Логарифм 0,03918 дорівнює −1.4069, або
\[0.03918=10^{-1.4069}=\dfrac{1}{10^{1.4069}} \nonumber \]
Щоб отримати загальний логарифм числа, скористайтеся кнопкою журналу на калькуляторі. Щоб обчислити число з його логарифма, візьміть зворотний журнал логарифма, або обчисліть 10 х (де х - логарифм числа).
Натуральний логарифм числа (ln) - це ступінь, до якої e потрібно підняти рівне число; e - постійна 2.7182818. Наприклад, натуральний логарифм 10 дорівнює 2,303; тобто
\[10=e^{2.303}=2.7182818^{2.303} \nonumber \]
Щоб отримати натуральний логарифм числа, скористайтеся кнопкою ln на калькуляторі. Щоб обчислити число з його натурального логарифма, введіть натуральний логарифм і візьміть обернений ln натурального логарифма, або обчисліть e x (де x - натуральний логарифм числа).
Логарифми є показниками; таким чином, операції з логарифмами дотримуються тих же правил, що й операції з експонентами.
- Логарифм добутку двох чисел - це сума логарифмів двох чисел. \[\log xy= \log x + \log y, \textrm{ and }\ln xy=\ln x + \ln y \nonumber \]
- Логарифм числа, отриманого в результаті ділення двох чисел, є різницею між логарифмами двох чисел. \[\log\dfrac{x}{y}=\log x-\log y,\textrm{ and } \ln\dfrac{x}{y}=\ln x-\ln y \nonumber \]
- Логарифм числа, зведеного до показника, є добутком показника і логарифма числа. \[\log x^n=n\log x \textrm{ and }\ln x^n=n\ln x \nonumber \]
Розв'язок квадратних рівнянь
Математичні функції цієї форми відомі як поліноми другого порядку або, частіше, квадратичні функції.
\[ax^2+bx+c=0 \nonumber \]
Розв'язок або коріння для будь-якого квадратного рівняння можна обчислити за такою формулою:
\[x=\dfrac{-b±\sqrt{b^2−4ac}}{2a} \nonumber \]
Розв'язування квадратних рівнянь Розв'яжіть квадратне рівняння 3 x 2 + 13 x − 10 = 0.
Розчин Підставивши значення a = 3, b = 13, c = −10 в формулу, отримаємо
\[x=\dfrac{−13±\sqrt{(13)^2−4×3×(−10)}}{2×3} \nonumber \]
\[x=\dfrac{−13±\sqrt{169+120}}{6}=\dfrac{−13±\sqrt{289}}{6}=\dfrac{−13±17}{6} \nonumber \]
Отже, два корені
\[x=\dfrac{−13+17}{6}=\dfrac{2}{3}\textrm{ and }x=\dfrac{−13−17}{6}=−5 \nonumber \]
Квадратичні рівняння, побудовані на фізичних даних, завжди мають реальне коріння, і з цих реальних коренів часто тільки ті, що мають позитивні значення, мають будь-яке значення.
Двовимірна (x - y) графіка
Зв'язок між будь-якими двома властивостями системи може бути представлений графічно двовимірним графіком даних. Такий графік має дві осі: горизонтальну, відповідну незалежній змінній, або змінну, значення якої контролюється (x), і вертикальну вісь, відповідну залежної змінної, або змінну, значення якої спостерігається або вимірюється (y).
Коли значення y змінюється як функція x (тобто різні значення x відповідають різним значенням y) графік цієї зміни може бути нанесений або ескізний. Графік може бути створений за допомогою певних значень для пар даних (x, y).
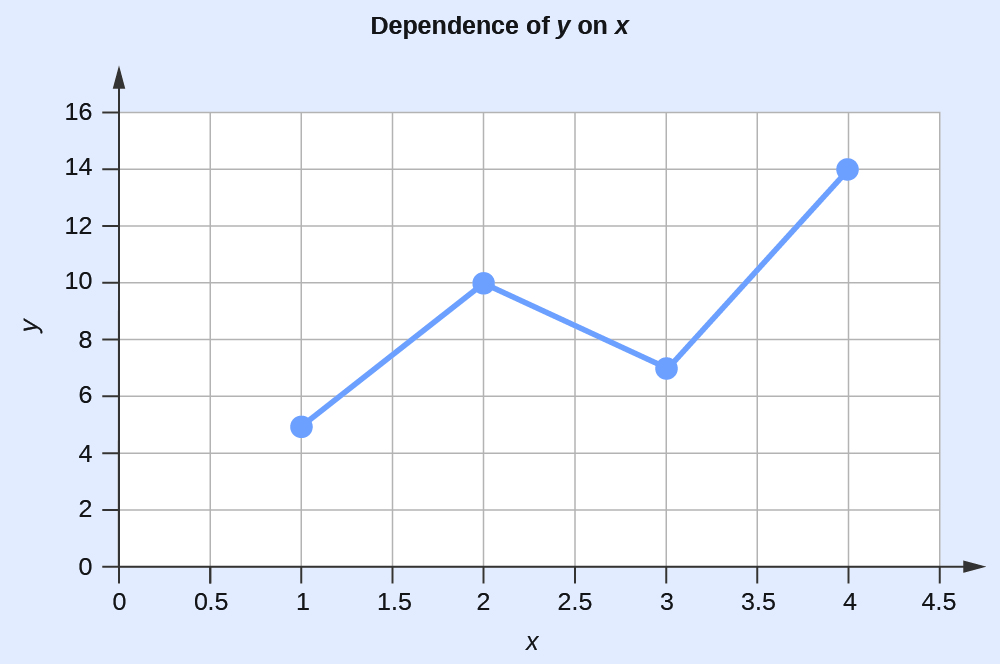
Графік залежності y від x
| х | у |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | 7 |
| 4 | 14 |
Ця таблиця містить наступні пункти: (1,5), (2,10), (3,7) та (4,14). Кожна з цих точок може бути побудована на графіку і з'єднана для отримання графічного зображення залежності y від x.
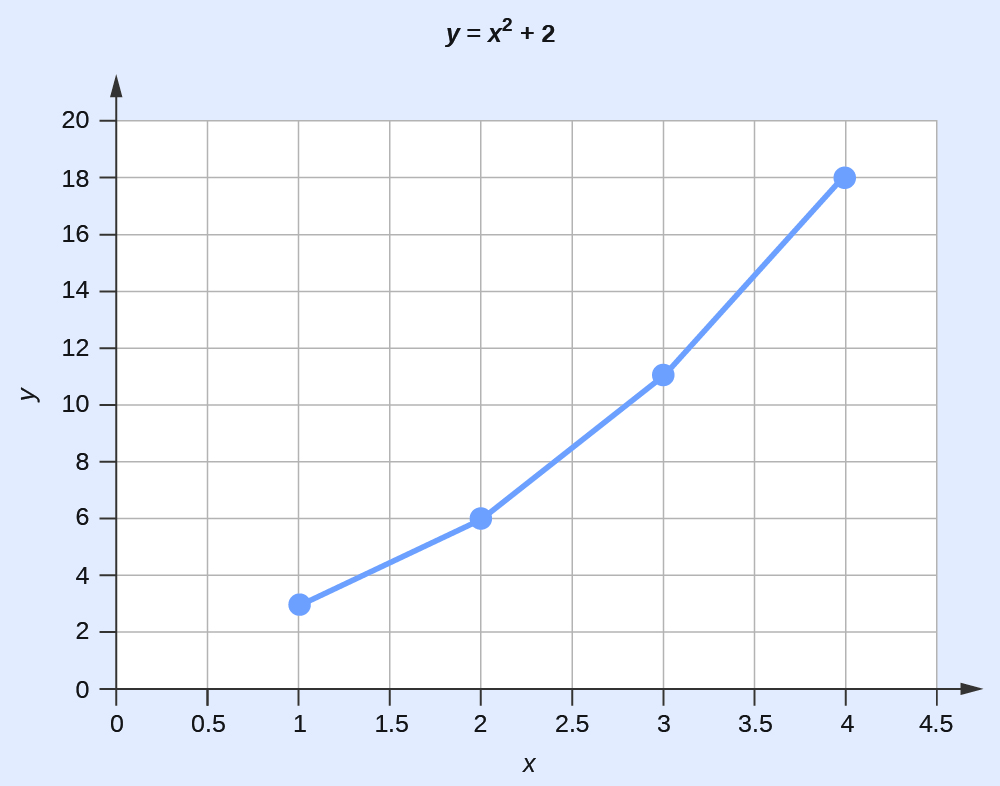
Якщо відома функція, яка описує залежність y від x, вона може бути використана для обчислення пар даних x, y, які згодом можуть бути побудовані.
Plotting Data Pairs If we know that y = x2 + 2, we can produce a table of a few (x,y) values and then plot the line based on the data shown here.
| x | y = x2 + 2 |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 11 |
| 4 | 18 |