9.3: Тиск

Ви, напевно, знайомі із загальним уявленням про тиск від досвіду в накачуванні шин або стисканні повітряних куль. Газ чинить силу на будь-якій поверхні, з якою він контактує. Сила на одиницю площі поверхні називається тиском і представлена P. Символи F і A представляють силу і площу відповідно. На зображенні нижче сила штовхає вниз на кругову область барометра. Тиск - це величина сили, що штовхає на одиницю площі кола барометра.

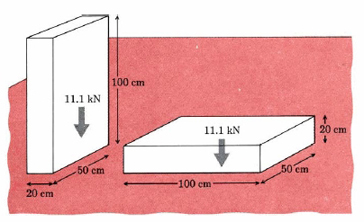
\[\text{Pressure}=\frac{\text{force}}{\text{area}}\text{ }P=\frac{F}{A} \nonumber \]Як простий приклад тиску розглянемо прямокутний блок свинцю, який вимірює 20,0 см на 50,0 см на 100,0 см (рис.\(\PageIndex{1}\)). Обсяг V блоку 1,00 × 10 ⁵ см ³, а так як щільність ρ Pb дорівнює 11,35 г см ^—3, маса m дорівнює

\[m=V\rho =\text{1}\text{.00 }\times \text{ 10}^{\text{5}}\text{ cm}^{\text{3}}\text{ }\times \text{ }\frac{\text{11}\text{.35 g}}{\text{1 cm}^{\text{3}}}\text{ }\label{1} =\text{1}\text{.135 }\times \text{ 10}^{\text{6}}\text{ g}=\text{1}\text{.135 }\times \text{ 10}^{\text{3}}\text{ kg} \]

Малюнок\(\PageIndex{1}\) Коли блок стоїть вертикально, вага блоку (11,1 кН) розподіляється на площі 0,1 м ³. Покладена рівно, ця ж сила тепер чиниться на площі в 5 разів більше (0,5 м ³), надаючи тиск в 5 разів менше, ніж раніше, навіть незважаючи на те, що вага блоку залишається колишнім.

Згідно з другим законом руху, виявленим британським фізиком Ісааком Ньютоном, сила на предмет є добутком маси об'єкта і його прискорення a:

\[F = ma\label{4} \]
На поверхні землі прискорення сили тяжіння становить 9,81 м с ^—2. Підставляємо масу свинцевого блоку в Eq. \(\ref{4}\), у нас є

\[F = 1.135 \times 10^{3} \text{ kg} \times \text{ m }\text{s}^{\text{-2}} = 11.13 \times 10 \text{ kg} \text{ m}\text{ s}^\text{-2} \nonumber \]Одиницям кілограма на квадратний секунду дається назва Ньютон в Міжнародній системі і скорочено N. Таким чином сила, яку сила тяжіння чинить на свинцевий блок (вага блоку) становить 11,13 × 10 ³ Н. Блок, який спирається на підлогу, буде завжди надають низхідну силу 11,13 кН. Тиск, що чиниться на підлогу, залежить від площі, на яку ця сила чиниться. Якщо блок спирається на 20,0 см на сторону 50,0 см (рис. 9.2 а), його вага розподіляється по площі 20,0 см × 50,0 см = 1000 см ³. Таким чином:

\[P=\frac{F}{A}=\frac{\text{11}\text{.13 kN}}{\text{1000 cm}^{\text{2}}}=\frac{\text{11}\text{.13 kN}}{\text{1000 cm}^{\text{2}}}\text{ }\times \text{ }\left( \frac{\text{100 cm}}{\text{1 m}} \right)^{\text{2}} =\frac{\text{11}\text{.13 kN}}{\text{10}^{\text{3}}\text{ cm}^{\text{2}}}=\frac{\text{10}^{\text{4}}\text{ cm}^{\text{2}}}{\text{1 m}^{\text{2}}}=\text{111}\text{.3 }\frac{\text{kN}}{\text{m}^{\text{2}}} =\text{111}\text{.3 }\times \text{ 10}^{\text{3}}\text{ N m}^{-\text{2}} \nonumber \]

Таким чином ми бачимо, що тиск можна виміряти в одиницях ньютонів (сили) на квадратний метр (площа). Одиниці Ньютон на квадратний метр використовуються в Міжнародній системі для вимірювання тиску, і їм дається назва паскаль (скорочено Па). Як і ньютон, Паскаль вшановує відомого вченого, в даному випадку Блеза Паскаля (1623 - 1662), одного з найдавніших дослідників тиску рідин і газів.

Якщо свинцевий блок прокладений на бік (рис. 1 б), тиск змінюється. Площа зіткнення з підлогою тепер становить 50,0 см × 100,0 см = 5000 см ², і так

\[P=\frac{F}{A}=\frac{\text{11}\text{.13 }\times \text{ 10}^{\text{3}}\text{ N}}{\text{5000 cm}^{\text{2}}}=\frac{\text{11}\text{.13 }\times \text{ 10}^{\text{3}}\text{ N}}{\text{0}\text{.500 m}^{\text{2}}} =\text{22}\text{.26 }\times \text{ 10}^{\text{3}}\text{ N m}^{-\text{2}}=\text{22}\text{.26 kPa} \nonumber \]Коли блок лежить рівно, його тиск на підлогу (22,26 кПа) становить лише одну п'яту таку ж велику, як тиск (111,3 кПа), коли він стоїть на кінці. Це пояснюється тим, що площа контакту в 5 разів більше.

Повітря, що оточує землю, тягнеться до поверхні гравітацією так само, як і головний блок, який ми обговорювали. Отже, повітря також чинить тиск на поверхню. Це називається атмосферним тиском.

У наступному відео показана «сила» атмосферного тиску. Металева банка, наповнена водою, нагрівається до тих пір, поки вода всередині не закипить, створюючи високий внутрішній тиск. Банку покласти догори дном в миску з холодною крижаною водою, в результаті чого раніше гаряча водяна пара охолоджується і зменшується в об'ємі. Таке охолодження викликає зниження внутрішнього тиску банки. Нижній тиск надає меншу силу на банку і більше не може протистояти атмосферному тиску, що надходить ззовні банки, який штовхає всередину, роздавлюючи банку.

Оскільки вітри можуть додавати більше повітря або забирати трохи від вертикальної колони над заданою площею на поверхні, атмосферний тиск буде змінюватися вище і нижче результату, отриманого в прикладі 9.1. Тиск також зменшується, коли людина рухається на більш високі висоти. Вершини Гімалаїв, найвищих гір у світі на відстані близько 8000 м (майже 5 миль), знаходяться вище більш ніж половини атмосфери. Нижній тиск на таких висотах дуже ускладнює дихання - навіть найменша напруга залишає одне задихається і слабке. З цієї причини реактивні літаки, які регулярно літають на висотах від 8 до 10 км, мають обладнання для штучного підтримки тиску повітря в своїх кабінках.

Часто зручно виражати тиск за допомогою одиниці, яка приблизно така ж, як середній атмосферний тиск на рівні моря. Як ми бачили в прикладі 1, атмосферний тиск становить близько 101 кПа, а стандартна атмосфера (скорочено атм) визначається як рівно 101,325 кПа. Так як даний агрегат використовується часто, корисно пам'ятати, що

\[1 \text{ atm} = 101.325 \text{ kPa} \nonumber \]

Приклад\(\PageIndex{1}\): Atmospheric Pressure

Загальна маса повітря безпосередньо над ділянкою Атлантичного океану 30 см на 140 см становила 4,34 × 10 ³ кг 27 липня 1977 року. Розрахуйте тиск, що чиниться на поверхню води атмосферою.

Рішення Спочатку розрахуйте силу гравітаційного тяжіння на повітрі:

\[F = ma = 4.34 \times 10^{3} \text{ kg} \times 9.81 \text{ m }\text{s}^{\text{-2}} = 4.26 \times 10^{4} \text{ kg m s}^\text{-2} = 4.26 \times 10^{4} \text{ N} \nonumber \]Площа - це

\[A=\text{30 cm }\times \text{ 140 cm}=\text{4200 cm}^{\text{2}}\text{ }\times \text{ }\left( \frac{\text{1 m}}{\text{100 cm}} \right)^{\text{2}}\text{ }=\text{0}\text{.42 m}^{\text{2}} \nonumber \]

Таким чином тиск\[P=\frac{F}{A}=\frac{\text{4}\text{.26 }\times \text{ 10}^{\text{4}}\text{ N}}{\text{0}\text{.42 m}^{\text{2}}}=\text{1}\text{.01 }\times \text{ 10}^{\text{5}}\text{ Pa}=\text{101 kPa} \nonumber \]