15.3: Другий закон термодинаміки
- Page ID
- 19341
Очікується, що ви зможете визначити та пояснити значення термінів, визначених зеленим типом.
- При будь-якому макроскопічному зміні ентропія світу (тобто система + оточення) завжди збільшується; вона ніколи не зменшується.
- Процеси, які не обмінюються теплом з навколишнім середовищем (наприклад, вільне розширення газу у вакуум), передбачають зміну ентропії системи самостійно і завжди спонтанні.
- Тепловий двигун - це пристрій, який перетворює тепло в роботу. Частка тепла, яка може бути перетворена в роботу, обмежується падінням температури між входом в двигун і вихлопом.
- Згідно з Другим Законом термодинаміки, повне перетворення тепла в роботу спонтанним циклічним процесом неможливо.
Перший закон термодинаміки, виражений як Δ U = q + w, по суті є твердженням закону збереження енергії. Значення цього закону полягає в тому, що він говорить нам про те, що будь-який запропонований процес, який би порушив цю умову, може бути відхилений як неможливий, навіть не допитуючись до деталей процесу.
Чому Першого Закону недостатньо?
Для простих механічних операцій на макроскопічних об'єктах Перший Закон, збереження енергії - це все, що нам зазвичай потрібно для визначення таких речей, як скільки джоулів енергії потрібно, щоб підняти вагу або закип'ятити трохи води, скільки грамів глюкози ви повинні метаболізувати, щоб піднятися на гірку, або скільки палива. ваш автомобіль повинен проїхати задану відстань.
Але якщо задуматися, існує ряд «простих механічних операцій», які ніколи не відбуваються, навіть якщо вони не порушували б енергозбереження.
- Припустимо, ви кидаєте книгу на стільницю. Кінетична енергія, що міститься в падаючій книзі, розсіюється як теплова енергія, злегка зігріваючи книгу і стільницю. Згідно з Першим Законом, немає причин, чому розміщення попередньо розігрітої книги на утепленій стільниці не повинно мати можливості повернути книгу назад в повітря. Так само, чому не може енергія, що передається цвяху (і дереву) молотком, не може вискочити цвях назад?
- Можна запропонувати схему руху судна за допомогою машини, яка приймає морську воду, витягує частину її теплової енергії, яка використовується для обертання гвинта, а потім кидає отримані кубики льоду за борт. Поки робота, виконана для повороту гвинта, не перевищує тепло, необхідне для розтоплення льоду, Перший Закон задовольняється.
- Оскільки рух молекул повітря є абсолютно випадковим, немає жодної причини, чому всі молекули в одній половині кімнати не можуть раптово «вирішити» перейти в іншу половину, задушивши нещасних мешканців цієї сторони. (В тій мірі, в якій повітря поводиться як ідеальний газ, це взагалі не стосується Першого Закону.)
Що спільного у всіх цих сценаріях, які відповідають Першому Закону, але, тим не менш, ніколи не зустрічаються? У кожному випадку енергія стає менш розкинутою, менше «розбавляється». У перших двох прикладах теплова енергія (дисперсна) концентрується в організовану кінетичну енергію макроскопічного об'єкта — книги, пропелера. У третьому випадку теплова енергія концентрується в меншому обсязі в міру контракту газу.
Другий закон термодинаміки фактично говорить, що ступінь, в якій може відбуватися будь-який природний процес, обмежується розведенням теплової енергії (збільшення ентропії), яка супроводжує її, і як тільки зміна відбулася, вона ніколи не може бути знята, не поширюючи ще більше енергії навколо. Це один з найглибших законів природи, і повинен бути частиною світогляду кожної освіченої людини. Прикро, що цей закон настільки широко спотворюється, як просто визначив збільшення «безладу». Більш коротке твердження Другого Закону (для тих, хто знає значення «ентропія») є
Другий закон термодинаміки: Ентропія світу лише збільшується і ніколи не зменшується.
Більш формальні та історичні способи викладання Другого Закону будуть представлені далі після того, як ми ознайомимо з темою теплових двигунів. Також варто знати це важливе наслідок Другого Закону: Просто тому, що енергія «там», не означає, що вона буде доступна робити що-небудь корисне.
Ентропія і спонтанні зміни
Ми пояснили, як процеси, які відбуваються спонтанно, завжди протікають у напрямку, що призводить до поширення та обміну тепловою енергією.
- Книга падає на стільницю (а не поглинає тепло і стрибає з неї), оскільки її кінетична енергія змінюється в теплову енергію, яка широко розсіюється в молекулах книги та столу.
- Газ розширюється і розчини змішуються, оскільки теплова енергія, яку мають їх молекули, поширюється на більший об'єм простору.
- Газ водню дисоціюється на атоми Н, які поділяють теплову енергію між більшою кількістю частинок і більшим об'ємом простору. (Але тільки якщо температура досить висока, щоб зробити величезну кількість нових мікростанів енергетично доступними.)
Оскільки всі природні процеси призводять до поширення і обміну теплової енергії, а тому, що ентропія є мірою того, наскільки енергія розсіюється в світі, випливає, що:
При будь-якому спонтанному макроскопічному зміні ентропія світу збільшується.
Всі природні процеси, що дозволяють вільний обмін тепловою енергією між хімічно значущими числами частинок, супроводжуються поширенням або «розведенням» енергії, яка залишає світ назавжди зміненим. Іншими словами, всі спонтанні зміни призводять до збільшення ентропії світу. На перший погляд це може здатися невідповідним нашим спостереженням дуже поширених випадків, коли спостерігається явне зниження ентропії, наприклад, заморожування рідини, утворення осаду або зростання організму.
Система + оточення = світ!
... але це ентропія системи плюс оточення, що враховує! Важливо розуміти, що критерієм спонтанної зміни є зміна ентропії системи та оточення— тобто «світу», який ми позначимо загальним Δ S:
\[ΔS_{total} = ΔS_{system} + ΔS_{surroundings} \label{23.1}\]
Єдиний спосіб вплинути на ентропію оточення - це обмін теплом з системою:
\[ΔS_{surroundings} = \dfrac{q_{surr}}{ T} \label{23.2}\]
Таким чином, замерзання води супроводжується потоком тепла (теплотою плавлення) в навколишнє середовище, що призводить до збільшення ΔS surr. При температурах нижче температури замерзання це підвищення з лишком компенсує зниження ентропії самої води, тому ΔsWorld перевищує нуль і процес мимовільний. Приклад проблеми нижче детально опрацьовує це для конкретного прикладу.
Зверніть увагу, що не має значення, чи відбувається зміна системи оборотно чи необоротно; як згадувалося раніше, завжди можна визначити альтернативний (незворотний) шлях, в якому кількість тепла, що обмінюється з навколишнім середовищем, така ж, як q rev; тому що Δ S - функція стану, зміна ентропії оточення матиме те саме значення, що і для нездійсненного оборотного шляху.
Якщо немає потоку тепла в навколишнє середовище або з нього, зміна ентропії системи та системи світу ідентичні. Прикладами таких процесів, які завжди є спонтанними, є вільне розширення ідеального газу в вакуум, і змішування двох ідеальних газів. На практиці практично всі процеси, пов'язані з змішуванням і дифузією, можуть розглядатися як обумовлені виключно ентропійним збільшенням системи.
Більшість процесів, що включають хімічні та фазові зміни, включають обмін теплом з навколишнім середовищем, тому їх тенденцію до виникнення не завжди можна передбачити, зосередивши увагу лише на системі. Далі, завдяки терміну — Q/t в середовищі Δ S спонтанність усіх таких процесів буде залежати від температури, як ми проілюстрували для дисоціації H 2 раніше.
Як кількісний приклад розглянемо замерзання води. Ми знаємо, що рідка вода мимовільно перетворюється на лід, коли температура опуститься нижче 0° C при тиску 1 атм. Оскільки ентропія твердої речовини менше, ніж у рідини, ми знаємо, що ентропія води (система тут) зменшиться при замерзанні. Величина зниження виявляється шляхом ділення тепла злиття льоду на температуру для оборотного шляху, що відбувається при нормальній точці замерзання:
\[ΔS_{system} = \dfrac{-6000 \; J/mol}{273 \;K} = -21.978 \; J/mol\]
Якщо процес фактично здійснюється при 0° C, то тепло плавлення передається навколишньому середовищу при тій же температурі, а ентропія оточення збільшується на
\[ΔS_{surroundings} = \dfrac{6000 \; J/mol}{273 \;K} = 21.979\; J/mol\]
так що Δ S загальна = 0. За цих умов процес може протікати в будь-якому напрямку (заморожування або танення), не впливаючи на ентропію світу; це означає, що і лід, і рідка вода можуть бути присутніми одночасно без будь-яких змін; система, як кажуть, знаходиться в рівновазі.
Припустимо тепер, коли вода переохолоджується до —1°C, перш ніж вона замерзне. Зміна ентропії води все ще відповідає оборотному значенню q rev/T = (—6000J)/(273K). Однак ентропійна зміна оточення тепер дається
\[ΔS_{surroundings} = \dfrac{6000 \; J/mol}{273 \;K} = 22.059\; J/mol\]
Загальна зміна ентропії зараз
\[ΔS_{total} = (–21.978 + 22.059) J;\ K^{–1} mol^{–1} = +0.081\; J \;K^{–1} mol^{–1}\]
вказуючи на те, що процес тепер може відбуватися («спонтанно») тільки в одному напрямку.
Чому ми використовували 273 K при оцінці Δ S системи і 272 K для обчислення Δ S оточення? В останньому випадку можна сформулювати оборотний шлях, за допомогою якого тепло може передаватися навколишньому середовищу при будь-якій температурі. Δ S система, однак, є державною функцією води, і буде змінюватися в залежності від температури лише незначно.
Зверніть увагу, що для того, щоб насправді заморозити воду, її потрібно охолодити до дуже трохи нижче нормальної температури замерзання, стан, відомий як переохолодження. Заморожування переохолодженої води, звичайно, є незворотним процесом (як тільки він почнеться, його не можна зупинити, крім як піднявши температуру на кінцеву кількість), і позитивне значення\(ΔS_{total}\) говорить нам про те, що цей процес буде відбуватися спонтанно при температурах нижче 273 К. При цих умовах процес обумовлюється збільшенням ентропії навколишнього середовища в результаті потоку тепла злиття води в навколишнє середовище.
Чи зменшується ентропія світу коли-небудь?
Принцип, згідно з яким теплова енергія (і несучі її молекули) має тенденцію до поширення, заснований на простій статистиці. Однак слід пам'ятати, що закони ймовірності мають значуще застосування лише до систем, що складаються з великої кількості незалежних суб'єктів. Якщо ви вловлюєте сотню мух у пляшці, вони, як правило, розподіляться більш-менш рівномірно по всьому контейнеру; однак, якщо мух всього чотири, цілком ймовірно, що всі вони зрідка будуть розташовуватися в одній конкретній половині пляшки.
Чому небо синє
Точно так само можна з повною впевненістю довіряти, що мимовільного руху половини молекул повітря в одну сторону кімнати, яку ви зараз займаєте, не відбудеться, навіть незважаючи на те, що молекули рухаються безладно і самостійно. З іншого боку, якщо розглядати коробку, розміри якої становлять лише кілька молекулярних діаметрів, то ми очікуємо, що випадкове та короткочасне зміщення невеликої кількості частинок, які вона містить, на одну сторону коробки відбуватиметься досить часто. Це, по суті, причина блакитності неба: випадкові коливання щільності повітря над крихітними обсягами простору, розміри яких можна порівняти з довжиною хвилі світла, призводить до вибіркового розсіювання коротших довжин хвиль, так що синє світло розсіюється, залишаючи червоне світло для насолода спостерігачами заходу сонця на схід.
Броунівський рух
Це стосується нерегулярного зигзагоподібного руху надзвичайно дрібних частинок, таких як пилок рослин, коли вони підвішені в краплі рідини. Будь-яка така частинка постійно буферується тепловими рухами навколишніх молекул рідини. Якщо розмір частинки дуже великий в порівнянні з молекулами рідини, сили, що виникають в результаті зіткнення цих молекул з частинкою, скасуються, і частка залишається непорушеною. Якщо ж частка дуже мала (можливо, всього в тисячу разів більше молекули рідини), то шанси на те, що вона зазнає досить більше ударів з одного боку, ніж з іншого за короткий проміжок часу, стають значними.
У цих двох прикладах ентропія системи зменшується без будь-якого компенсуючого потоку тепла в навколишнє середовище, що призводить до чистого (але лише тимчасового) зниження ентропії світу. Однак це не є провалом Другого Закону, оскільки ніхто ніколи не придумував спосіб витягти корисну роботу з цих процесів.
Теплові двигуни
Промислова революція 19 століття багато в чому була викликана винаходом парового двигуна. Першим основним використанням таких двигунів було відкачування води з шахт, затоплення яких від природного просочування серйозно обмежувало глибини, на які вони могли бути загнані, і, таким чином, наявність металевих руд, які мали важливе значення для розширення промислової діяльності. Паровий двигун - це тип теплового двигуна, пристрій, який перетворює тепло, що забезпечується спалюванням палива, в механічну роботу, як правило, доставляється через рух поршня на противагу силі. Таким чином, двигун є пристроєм перетворення енергії, в якому, в ідеалі, кожен джоуль тепла, що виділяється при згорянні палива, може бути витягнутий як робота на вихідному валу; такий двигун буде працювати зі 100-відсотковою ефективністю.
Однак інженери того часу були здивовані, виявивши, що ККД парових двигунів був досить низьким (зазвичай близько 20%), причому більша частина тепла вичерпується марно в навколишнє середовище. Всі розуміли, що ККД, що перевищує 100%, буде неможливим (що порушить збереження енергії, а отже, і Перший закон), але не було зрозуміло, чому ефективність не може значно піднятися за межі малих значень, що спостерігаються навіть у міру вдосконалення механічних конструкцій.

Відповідь знайшов молодий французький інженер Саді Карно, який у 1824 році опублікував аналіз ідеалізованого теплового двигуна, який, як правило, вважається основою науки про термодинаміку - незважаючи на те, що Карно все ще прийняв переконання, що тепло - це рідинна речовина, яка називається «калорійність». Ми не будемо копіювати його аналіз тут (це зазвичай робиться на більш просунутих курсах з фізичної хімії), а просто викладемо його висновок у власних [перекладених] словах:
«Виробництво рушійної сили відбувається тоді в парових двигунів не фактичним споживанням калорій, а її транспортуванням від теплого тіла до холодного тіла... вироблення тепла одного недостатньо, щоб народити силу, що штовхає: необхідно, щоб також було холодно; без нього спека була б марною. Гранична досяжна ефективність будь-якого теплового двигуна буде залежати від температур, при яких тепло подається і відводиться з нього».
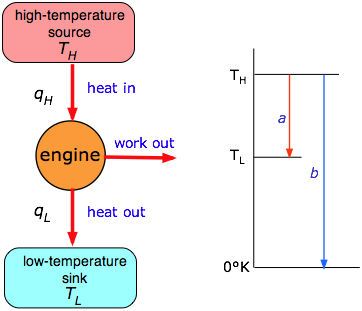
Ліва частина малюнка представляє узагальнений тепловий двигун, в який кількість тепла q H, витягнутого з джерела або «резервуара» при температурі T H, частково перетворюється в роботу w. Залишок тепла q L відводиться в резервуар при більш низькій температурі T L. На практиці T H буде температурою пари в паровому двигуні, або температурою суміші згоряння в двигуні внутрішнього згоряння або турбіни. Низькотемпературний резервуар, як правило, є резервуаром місцевого середовища. ККД ε (епсилон) теплового двигуна - це частка тепла, відведеного з високотемпературного резервуара, яке може бути перетворено в роботу:
\[ ε = \dfrac{w}{q_H} \label{3.3}\]
Найважливіший висновок Карно (за який він, безумовно, заслужив би Нобелівську премію, якби вони існували в той час) полягає в тому, що ефективність пропорційна «відстані» температури, яку тепло може «впасти», коли воно проходить через двигун:
\[ ε = 1 - \dfrac{T_L}{T_H} \label{3.4}\]
Це проілюстровано графічно в правій половині цифри трохи вище, в якій ККД - це просто частка «повного» падіння (в температурі) до абсолютного нуля (стрілка b), що тепло зазнає в двигуні (стрілка а.) Зрозуміло, що єдиним способом досягти 100% ефективності було б встановити температуру витяжного резервуара до 0° К, що було б неможливо. Для більшості наземних теплових двигунів T L - це лише температура навколишнього середовища, як правило, близько 300 К, тому єдиний практичний спосіб підвищити ефективність - зробити T H якомога вище. Це є причиною того, що на комерційних теплових електростанціях віддають перевагу пара високого тиску (перегріта). Найвищі температури (і найбільший ККД) отримують в газотурбінних двигунів. Однак, коли робочі температури зростають, витрати на боротьбу з більш високим тиском пари та здатність матеріалів, таких як лопатки турбін, витримувати високі температури, стають значними факторами, ставлячи верхню межу близько 600K на T H, таким чином встановлюючи максимум близько 50 відсотків. ККД на виробленні теплової енергії.
Для атомних станцій, в яких міркування безпеки вимагають більш низького тиску пари, ККД нижче. Одним з наслідків цього є те, що більша частка тепла вичерпується в навколишнє середовище, що може призвести до більшої шкоди водним організмам при поверненні охолоджуючої води в потік або лиман.
Було зроблено кілька пропозицій щодо побудови теплового двигуна, який використовує різницю температур між поверхневими водами океану та прохолоднішими водами, які, будучи більш щільними, проживають на більшій глибині. Якщо температура вихлопних газів становить 5° C, який максимальний обсяг роботи може бути витягнутий з 1000 л поверхневої води при 10° C? (Питома теплоємність води 4,184 Дж г —1 К —1.)
Рішення
Кількість тепла (q H), яке необхідно витягти для охолодження води на 5 К, становить (4,184 Дж г —1 К —1) (10 6 г) (5 К) = 2,09 × 10 7 Дж. Ідеальна термодинамічна ефективність задається
\[ 1 -\dfrac{278 \;K}{283\; K} = 0.018\]
Обсяг роботи, який можна було б виконати
\[(0.018)(2.09 \times 10^7 \;J) = 3.7 \times 10^6 \;J\]
Коментар: Це може бути лише 1.8% ефективним, але це безкоштовно!
Птах, що п'є як тепловий двигун
Мало хто з іграшок ілюструє стільки принципів фізичної науки, скільки це популярний пристрій, який існує вже багато років. На перший погляд це може здатися вічною машиною руху, але це насправді просто простий тепловий двигун. Сучасні «діппі птахи» (як їх іноді називають) використовують в якості робочої рідини дихлорметан.

Ця рідина закипає при 39° С, а тому має досить високий тиск пари при кімнатній температурі. Рідина (до якої часто додають барвник для драматичного ефекту) зберігається в резервуарі на дні птиці. Дзьоб птиці покритий повстю, який, на мить занурюючись у воду, створює охолоджуючий ефект у міру випаровування води. Це призводить до того, що деякі пари CH 2 Cl 2 конденсуються в голівці, знижуючи тиск всередині пристрою, внаслідок чого більше рідини википає і знову конденсується в голівці. Перерозподіл рідини порушує рівновагу, змушуючи птицю занурювати дзьоб назад у воду. Як тільки голова наповнюється рідиною, вона стікає назад в дно, перекидаючи птицю вертикально, щоб повторити цикл.
Ми залишимо вам пов'язати це з наведеною вище схемою теплового двигуна, визначивши джерело тепла та раковину, і оцінити термодинамічний ККД двигуна.
Теплові насоси
Якщо тепловий двигун запускається «в зворотному напрямку», виконуючи на ньому роботи (тобто змінюючи «відпрацювання» на «працювати в» на рис. 8), він стає пристроєм для транспортування тепла проти теплового градієнта. Холодильники і кондиціонери - найбільш часто зустрічаються теплові насоси. Тепловий насос також може бути використаний для обігріву інтер'єру будівлі. При цьому застосуванні низькотемпературний резервуар може бути теплообмінником, заглибленим в землю або зануреним в колодязь. При цьому застосування теплові насоси більш ефективні, ніж печі або електричне опалення, але капітальні витрати досить високі.
Другий закон: що він означає
Саме вищевказане спостереження Карно в кінцевому підсумку призвело до формулювання Другого закону термодинаміки ближче до кінця 19 століття. Одне з тверджень цього закону (Кельвіна і Планка) полягає в наступному:
Не можна, щоб циклічний процес, підключений до резервуара при одній температурі, виробляв позитивний обсяг роботи в навколишньому середовищі.
Щоб допомогти вам зрозуміти це твердження і те, як воно відноситься до теплових двигунів, розглянемо схему теплового двигуна на малюнку, в якому робоча рідина (гази згоряння або пара) розширюється проти стримуючої сили ваги, механічно пов'язаної з поршнем. З термодинамічної точки зору робоча рідина - це система, а все інше - оточення. Розширення рідини відбувається, коли вона поглинає тепло з навколишнього середовища; повернення системи в початковий стан вимагає, щоб навколишні робили роботу над системою. Тепер перечитайте вищевикладене твердження Другого Закону, звернувши особливу увагу на курсивом фрази, які пояснюються нижче:
- Циклічний процес - це той процес, при якому система повертається в початковий стан. Простий паровий двигун зазнає крок розширення (силовий хід), після чого відбувається стиснення (хід вихлопу), при якому поршень, а значить і двигун, повертається в початковий стан до повторення процесу.
- «При одній температурі» означає, що ступені розширення і стиснення працюють ізотермічно. Це означає, що ΔU = 0; якраз достатньо тепла поглинається системою для виконання робіт, необхідних для підняття ваги, тому для цього кроку q = —w.
- «Позитивний обсяг роботи в оточенні» означає, що двигун робить більше роботи над оточенням, ніж оточення робить на двигуні. Без цієї умови двигун був би марним.
Уважно зауважте, що Другий Закон застосовується лише до циклічного процесу - ізотермічне розширення газу проти ненульового тиску завжди працює на навколишньому середовищі, але двигун повинен повторювати цей процес постійно; для цього його потрібно повернути до початкового стану наприкінці кожного циклу. При роботі ізотермічно робота - w вона робить на навколишньому середовищі на етапі розширення (силовий удар) зводиться нанівець роботою + w оточення повинно зробити в системі, щоб завершити цикл. Другий Закон також може бути викладений альтернативним способом:
Неможливо сконструювати машину, що працює циклами, яка буде перетворювати тепло в роботу, не виробляючи ніяких інших змін.
Таким чином, Другий Закон дозволяє двигуну перетворювати тепло в роботу, але тільки якщо дозволені «інші зміни» (передача частини тепла безпосередньо в навколишнє середовище). А оскільки тепло може тільки мимовільно надходити від джерела при більш високій температурі до раковини при більш низькій температурі, мається на увазі неможливість ізотермічного перетворення тепла в роботу.
