15.2: Правила ентропії
- Page ID
- 19345
Очікується, що ви зможете визначити та пояснити значення термінів, виділених жирним шрифтом.
- Реверсивний процес - це той, що здійснюється в нескінченнімалі етапи, після яких при скасуванні і система, і оточення (тобто світ) залишаються незмінними (див. Приклад газового розширення-стиснення нижче). Хоча справжня оборотна зміна не може бути реалізована на практиці, її завжди можна наблизити.
- ((В якому здійснюється процес.
- Оскільки процес здійснюється більш оборотним способом, значення w наближається до максимально можливого значення, а q наближається до мінімально можливого значення.
- Хоча q не є функцією стану, частка q rev/T є і відома як ентропія.
- енергії всередині системи.
- Ентропія речовини збільшується з його молекулярною масою та складністю, а також з температурою. Ентропія також збільшується, оскільки тиск або концентрація стають меншими. Ентропії газів набагато більше, ніж у конденсованих фаз.
- Абсолютна ентропія чистої речовини при заданій температурі - це сума всієї ентропії, яку вона придбає при потеплінні від абсолютного нуля (де S = 0) до конкретної температури.
Ентропія - одна з найбільш фундаментальних концепцій фізичної науки, з далекосяжними наслідками, починаючи від космології до хімії. Він також широко неправильно представлений як міра «розладу», про що ми обговорюємо нижче. Німецький фізик Рудольф Клаузіус зародив поняття як «енергія пішла в даремно» на початку 1850-х років, і його визначення пройшло через ряд більш точних визначень протягом наступних 15 років.
Раніше ми пояснювали, як схильність теплової енергії до максимально широкого розсіювання - це те, що рухає всіма спонтанними процесами, включаючи, звичайно, хімічні реакції. Тепер нам потрібно зрозуміти, як напрямок та ступінь поширення та розподілу енергії можуть бути пов'язані з вимірюваними термодинамічними властивостями речовин - тобто реагентів та продуктів.
Ви нагадаєте, що коли кількість тепла q тече від більш теплого тіла до більш прохолодного, що дозволяє наявної теплової енергії поширюватися в і заселяти більше мікростанів, це співвідношення q/T вимірює ступінь поширення цієї енергії. Виявляється, ми можемо узагальнити це і на інші процеси, але є труднощі з використанням q, оскільки це не функція стану; тобто її значення залежить від шляху або способу здійснення процесу. Це, звичайно, означає, що частка q/T також не може бути функцією стану, тому ми не можемо використовувати його для отримання відмінностей між реагентами та продуктами, як ми робимо з іншими функціями стану. Спосіб навколо цього полягає в тому, щоб обмежити наш розгляд особливим класом шляхів, які описуються як оборотні.
Оборотні та незворотні зміни
Кажуть, що зміна відбувається оборотно, коли вона може бути здійснена низкою нескінченно малих кроків, кожен з яких можна скасувати, зробивши аналогічну хвилину зміни умов, які призводять до змін. Наприклад, реверсивне розширення газу може бути досягнуто шляхом зменшення зовнішнього тиску в серії нескінченно малих кроків; реверсивний будь-який крок поверне систему та оточення до попереднього стану. Аналогічно, тепло може передаватися оборотно між двома тілами, змінюючи різницю температур між ними нескінченно малими кроками, кожен з яких може бути скасований шляхом зміни різниці температур.
Найбільш широко наведений приклад незворотної зміни - вільне розширення газу в вакуум. Хоча систему завжди можна відновити до початкового стану шляхом повторного стиснення газу, для цього буде потрібно, щоб оточення виконувало роботу на газі. Оскільки газ не працює на навколишнє у вільному розширенні (зовнішній тиск дорівнює нулю, тому P Δ V = 0,) відбудеться постійна зміна оточення. Іншим прикладом незворотних змін є перетворення механічної роботи в тепло тертя; немає можливості, повертаючи рух ваги вздовж поверхні, щоб тепло, що виділяється внаслідок тертя, не може бути відновлено системі.
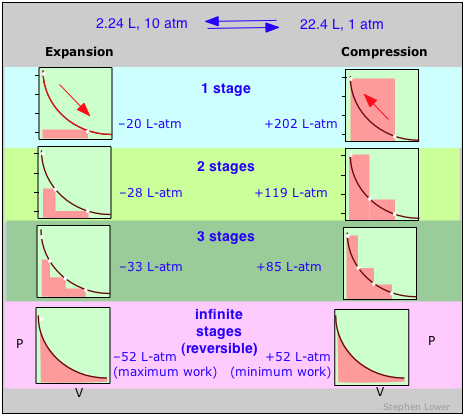
Ці діаграми показують однакове розширення і стиснення ± ΔV, що виконуються в різній кількості кроків, починаючи від одного кроку вгорі до «нескінченного» числа кроків внизу. Зі збільшенням кількості кроків процеси стають менш незворотними; тобто різниця між роботою, виконаною при розширенні, і необхідною для повторного стиснення газу зменшується. У межі «нескінченного» числа кроків (знизу) ці терміни роботи ідентичні, і як система, так і оточення («світ») незмінні циклом розширення-стиснення. У всіх інших випадках система (газ) відновлюється до початкового стану, але оточення назавжди змінено.
Оборотна зміна здійснюється таким чином, що при скасуванні і система, і оточення (тобто світ) залишаються незмінними.
Звичайно, слід сказати, що будь-який процес, який протікає нескінченно малими кроками, займе нескінченно багато часу, тому термодинамічна оборотність - це ідеалізація, яка ніколи не досягається в реальних процесах, за винятком випадків, коли система вже знаходиться в рівновазі, і в цьому випадку ніяких змін не відбудеться. ! Так чому ж поняття оборотного процесу так важливо?
Відповідь можна побачити, нагадавши, що зміна внутрішньої енергії, що характеризує будь-який процес, може розподілятися в нескінченності шляхів між тепловим потоком через межі системи і роботою, виконаною на або системою, що виражається Першим Законом Δ U = q + ш. Кожна комбінація q і w являє собою різний шлях між початковим і кінцевим станами. Можна показати, що оскільки такий процес, як розширення газу, здійснюється послідовно довшими серіями менших кроків, абсолютне значення q наближається до мінімуму, а значення w наближається до максимуму, характерного для конкретного процесу.
Таким чином, коли процес здійснюється оборотно, w -термін у виразі Першого Закону має своє максимально можливе значення, а q -член - найменший. Ці спеціальні величини w max і q min (які ми позначаємо як q rev і вимовляємо «q-оборотний») мають унікальні значення для будь-якого заданого процесу і тому є функціями стану.
Робота і оборотність
Для процесу, який оборотно обмінюється кількістю тепла q rev з оточенням, зміна ентропії визначається як
\[ \Delta S = \dfrac{q_{rev}}{T} \label{23.2.1}\]
Це основний спосіб оцінки Δ S для процесів з постійною температурою, таких як фазові зміни або ізотермічне розширення газу. Для процесів, в яких температура не є постійною, таких як нагрівання або охолодження речовини, рівняння повинна бути інтегрована в необхідний температурний діапазон, як розглянуто нижче.
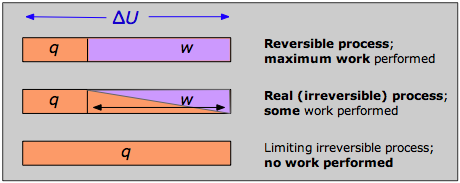
Якщо жоден реальний процес не може відбутися оборотно, яке використання є виразом, що включає q rev? Це досить тонкий момент, який ви повинні зрозуміти: хоча передача тепла між системою та навколишнім середовищем неможливо досягти по-справжньому оборотним чином, цей ідеалізований шлях має вирішальне значення лише для визначення Δ S; в силу того, що він є функцією стану, те саме значення з Δ S застосовуватиметься, коли система зазнає тієї ж чистої зміни через будь-який шлях. Наприклад, зміна ентропії газу зазнає, коли його обсяг подвоюється при постійній температурі, буде однаковою незалежно від того, чи здійснюється розширення в 1000 крихітних кроків (настільки оборотним, як терпіння, ймовірно, дозволить) або однокроковим (як незворотний шлях, який ви можете отримати!) розширення в вакуум.
Фізичний сенс ентропії
Ентропія - це міра ступеня поширення і розподілу теплової енергії всередині системи. Це «поширення та обмін» може бути поширенням теплової енергії у більший об'єм простору або її розподілом між раніше недоступними мікростанами системи. Наступна таблиця показує, як це поняття застосовується до ряду загальних процесів.
| система і процес | джерело ентропії підвищення системи |
|---|---|
| Колода карт перетасовується, або 100 монет, спочатку головами вгору, випадковим чином кидаються. | Це не має нічого спільного з ентропією, оскільки макрооб'єкти не в змозі обмінюватися тепловою енергією з оточенням протягом часового масштабу процесу. |
| Два однакових блоку з міді, один при 20°C, а інший при 40°С, розміщені в контакті. | Блок кулера містить більше незайнятих мікростанів, тому тепло тече від більш теплого блоку до тих пір, поки в двох блоках не буде заселено рівну кількість мікростанів. |
| Газ розширюється ізотермічно до подвійного його початкового об'єму. | Постійна кількість теплової енергії поширюється на більший обсяг простору |
| 1 моль води нагрівається на 1С°. | Збільшена теплова енергія робить доступними додаткові мікростани. (Збільшення становить приблизно 10 20 000 000 000 000 000 000 000 000 000.) |
| Рівні обсяги двох газів допускаються до змішування. | Ефект такий же, як дозволяє кожному газу розширюватися вдвічі більше його обсягу; теплова енергія в кожному тепер поширюється на більший обсяг. |
| Один моль дигідрогену, Н 2, поміщають в ємність і нагрівають до 3000К. | Частина Н 2 дисоціює до Н, оскільки при цій температурі в 2 молі H є більш термічно доступні мікростани. |
| Вищевказану реакційну суміш охолоджують до 300К. | Склад зміщується назад практично до всіх Н 2, оскільки ця молекула містить більш термічно доступні мікростану при низьких температурах. |
Ентропія - це велика кількість; тобто вона пропорційна кількості речовини в системі; таким чином, 100 г металевої міді має вдвічі більшу ентропію 50 г при тій же температурі. Це має сенс, оскільки більший шматок міді містить вдвічі більше квантованих рівнів енергії, здатних утримувати теплову енергію.
Ентропія і «розлад»
Ентропія все ще описується, особливо в старих підручниках, як міра розладу. У вузькому технічному сенсі це правильно, оскільки поширення та розподіл теплової енергії має ефект рандомізації розподілу теплової енергії всередині системи. Але просто прирівняти ентропію до «розладу» без подальшої кваліфікації вкрай оманливо, оскільки занадто легко забути, що ентропія (і термодинаміка взагалі) відноситься тільки до систем молекулярного рівня, здатних обмінюватися тепловою енергією з навколишнім середовищем. Перенесення цих понять до макросистем може дати переконливі аналогії, але це вже не наука. набагато краще взагалі уникати терміну «розлад» при обговоренні ентропії.

Ентропія і ймовірність
Розподіл теплової енергії в системі характеризується кількістю квантованих мікростанів, які доступні (тобто серед яких енергія може бути розділена); чим їх більше, тим більша ентропія системи. Це основа альтернативного (і більш фундаментального) визначення ентропії
\[\color{red} S = k \ln Ω \label{23.2.2}\]
в якій k - постійна Больцмана (газова константа на молекулу, 1,38 10 —23 J K —1) і Ω (омега) - кількість мікростанів, які відповідають заданому макростану системи. Чим більше таких мікростанів, тим більша ймовірність знаходження системи у відповідному макростані. Для будь-якого фізично реалізованого макростану величина Ω - це неймовірно велика кількість, як правило, навколо\(10^{10^{25}}\) для одного моля. Для порівняння, кількість атомів, що складають землю, приблизно\(10^{50}\). Але навіть незважаючи на те, що порівнювати цифри, які, здається, межують з нескінченністю, теплова енергія, що міститься в реальних фізичних системах, вдається виявити найбільшу з цих величин без особливих труднощів, швидко оселившись до найбільш ймовірного макростану для даного набору умови.
Причина S залежить від логарифма Ω легко зрозуміти. Припустимо, у нас дві системи (ємності з газом, скажімо) з S 1, Ω 1 і S 2, Ω 2. Якщо ми зараз переосмислимо це як єдину систему (фактично без змішування двох газів), то ентропія нової системи буде
\[S = S_1 + S_2\]
але кількість мікростанів буде добуток Ω 1 Ω 2 тому що для кожного стану системи 1 система 2 може бути в будь-якому з Ω 2 станів. Тому що
\[\ln(Ω_1Ω_2) = \ln Ω_1 + \ln Ω_2\]
Значить, адитивність ентропії зберігається.
Якщо хтось міг зняти фільм, який показує рухи окремих атомів газу або хімічної реакційної системи в її рівноважному стані, ви не зможете визначити, переглядаючи його, чи фільм грає в прямому чи зворотному напрямку. Фізики описують це тим, що такі системи мають симетрію зміни часу; ні класична, ні квантова механіка не дає жодної підказки до напрямку часу.
Однак, коли фільм, який показує зміни на макроскопічному рівні, відтворюється назад, дивацтво яскраво очевидно для будь-кого; якщо ви бачите книги, що злітають зі стільниці, або чай засмоктується назад у чайний пакетик (або хімічна реакція, що працює у зворотному напрямку), ви негайно дізнаєтесь, що щось не так. На цьому рівні час явно має напрямок, і часто відзначається, що оскільки ентропія світу в цілому завжди збільшується і ніколи не зменшується, саме ентропія дає час свій напрямок. Саме з цієї причини ентропію іноді називають «стрілою часу».
Але тут є проблема: звичайна термодинаміка здатна визначити зміну ентропії лише для оборотних процесів, які, як відомо, займають нескінченно багато часу. Тому ми стикаємося з очевидним парадоксом, що термодинаміка, яка займається лише відмінностями між станами, а не подорожами між ними, не в змозі описати той самий процес змін, за допомогою якого ми усвідомлюємо перебіг часу.
Напрямок часу виявляється хіміку прогресом реакції до її стану рівноваги; як тільки рівновага досягається, чиста зміна, яка призводить до неї, припиняється, і з точки зору цієї конкретної системи потік часу припиняється. Якщо поширити ту ж ідею на набагато більшу систему світу в цілому, то це призводить до поняття «теплової смерті Всесвіту», про яке коротко говорилося в попередньому уроці.
Абсолютні ентропії
Енергетичні значення, як відомо, всі відносні і повинні бути визначені за шкалою, яка є абсолютно довільною; немає такого поняття, як абсолютна енергія речовини, тому ми можемо довільно визначити ентальпію або внутрішню енергію елемента в його найбільш стабільній формі при 298K і 1 атм тиску як нуль. Те ж саме не стосується ентропії; оскільки ентропія є мірою «розведення» теплової енергії, то випливає, що чим менше теплової енергії, доступної для поширення через систему (тобто чим нижче температура), тим меншою буде її ентропія. Іншими словами, як абсолютна температура речовини наближається до нуля, так і його ентропія. Цей принцип лежить в основі Третього закону термодинаміки, який стверджує, що ентропія ідеально впорядкованого твердого тіла при 0 К дорівнює нулю.
Третій закон термодинаміки
Ентропія ідеально впорядкованого твердого тіла при 0 К дорівнює нулю.
Абсолютну ентропію речовини при будь-якій температурі вище 0 К необхідно визначити шляхом розрахунку приростів теплоти q, необхідних для доведення речовини від 0 К до потрібної температури, а потім підсумовуючи співвідношення q/T. Потрібні два види експериментальних вимірювань:
- Ентальпії, пов'язані з будь-якими фазовими змінами речовини, можуть зазнати в діапазоні температур, що цікавить. Плавлення твердої речовини та випаровування рідини відповідають значному збільшенню кількості мікростанів, доступних для прийняття теплової енергії, тому, як ці процеси відбуваються, енергія буде надходити в систему, заповнюючи ці нові мікростани в обсязі, необхідному для підтримки постійної температури (заморожування або температура кипіння); ці притоки теплової енергії відповідають теплом плавлення і випаровування. Збільшення ентропії, пов'язане з плавленням, наприклад, становить just t ΔH плавлення /T m.
- Теплоємність С фази виражає кількість тепла, необхідного для зміни температури на невелику величину Δ T, а точніше, на нескінченно малу величину dT. Таким чином, збільшення ентропії, спричинене нагріванням речовини в діапазоні температур, який не охоплює фазовий перехід, задається сумою величин C dT/t для кожного приросту температури dT. Це, звичайно, просто невід'ємна
\[ S_{0^o \rightarrow T^o} = \int _{o^o}^{T^o} \dfrac{C_p}{T} dt \]
Оскільки сама по собі теплоємність трохи залежить від температури, найбільш точні визначення абсолютних ентропій вимагають, щоб функціональна залежність С від Т використовувалася в вищезгаданому інтегралі замість постійної С.
\[ S_{0^o \rightarrow T^o} = \int _{o^o}^{T^o} \dfrac{C_p(T)}{T} dt \]
Коли це невідомо, можна провести серію вимірювань теплоємності над вузькими температурними кроками Δ T і виміряти площу під кожним ділянкою кривої на малюнку\(\PageIndex{3}\).
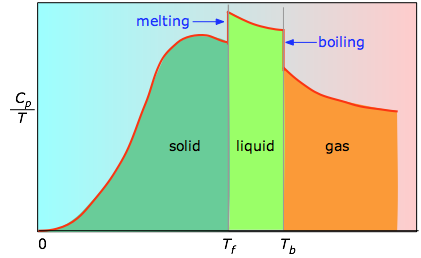
Площа під кожною ділянкою ділянки являє собою зміну ентропії, пов'язану з нагріванням речовини через інтервал Δ T. До цього слід додати ентальпії плавлення, випаровування та будь-яких змін твердої та твердої фази. Значення C p для температур поблизу нуля не вимірюються безпосередньо, але можуть бути оцінені з квантової теорії.
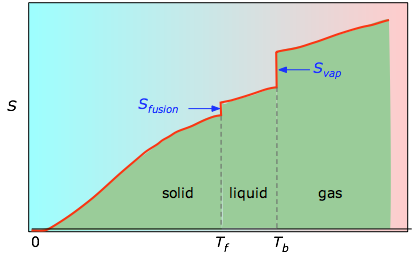
/Т б додаються для отримання абсолютної ентропії при температурі T. Як показано на малюнку\(\PageIndex{4}\) вище, ентропія речовини збільшується з температурою, і це відбувається з двох причин:
- З підвищенням температури стає доступним більше мікростанів, що дозволяє більш широко розсіюватися тепловій енергії. Це відбивається на поступовому збільшенні ентропії з температурою.
- Молекули твердих тіл, рідин та газів мають все більшу свободу пересування, полегшуючи поширення та обмін тепловою енергією. Тому фазові зміни супроводжуються масивним і переривчастим збільшенням ентропії.
Стандартні ентропії речовин
Стандартна ентропія речовини - його ентропія при тиску в 1 атм. Значення, знайдені в таблицях, зазвичай є значеннями для 298K, і виражаються в одиницях J K —1 моль —1. У таблиці нижче наведені деякі типові значення для газоподібних речовин.
| Він | 126 | Н 2 | 131 | СН 4 | 186 |
|---|---|---|---|---|---|
| Ne | 146 | N 2 | 192 | Н 2 О (г) | 187 |
| Ар | 155 | КО | 197 | СО 2 | 213 |
| Кр | 164 | Ф 2 | 203 | С 2 Ч 6 | 229 |
| Xe | 170 | О 2 | 205 | п -С 3 Н 8 | 270 |
| Сл 2 | 223 | п -С 4 Н 10 | 310 |
Особливо зверніть увагу на те, як значення, наведені в цій таблиці \(\PageIndex{2}\): ілюструють ці важливі моменти:
- Хоча стандартні внутрішні енергії та ентальпії цих речовин були б нульовими, ентропії не є. Це відбувається тому, що абсолютного масштабу енергії немає, тому ми умовно ставимо «енергії утворення» елементів в їх стандартних станах на нуль. Ентропія, однак, вимірює не саму енергію, а її розгін серед різних квантових станів, доступних для її прийняття, і вони існують навіть у чистих елементах.
- Очевидно, що ентропії, як правило, збільшуються з молекулярною масою. Для благородних газів це, звичайно, пряме відображення принципу, що поступальні квантові стани більш тісно упаковані в більш важкі молекули, що дозволяє їх займати.
- Ентропії двоатомних і багатоатомних молекул показують додаткові ефекти обертальних квантових рівнів.
| C (алмаз) | C (графіт) | Fe | Пб | Na | S (ромбічний) | СІ | Ш |
|---|---|---|---|---|---|---|---|
| 2.5 | 5.7 | 27.1 | 51.0 | 64.9 | 32.0 | 18.9 | 33.5 |
На ентропії твердих елементів сильно впливає спосіб, яким атоми пов'язані один з одним. Контраст між алмазом і графітом особливо вражає; графіт, який складається з нещільно зв'язаних штабелів гексагональних листів, здається більш ніж вдвічі краще при поглинанні теплової енергії, ніж алмаз, в якому атоми вуглецю щільно замкнені в тривимірну решітку, таким чином забезпечуючи їм менше можливості вібрувати навколо своїх рівноважних положень. Дивлячись на всі приклади в наведеній вище таблиці, ви відзначите загальну зворотну кореляцію між твердістю твердого тіла і його ентропією. Таким чином, натрій, який можна різати ножем, має майже вдвічі більшу ентропію заліза; набагато більша ентропія свинцю відображає як його високу атомну вагу, так і відносну м'якість цього металу. Ці тенденції узгоджуються з часто вираженим принципом, що чим більше «невпорядкована» речовина, тим більше його ентропія.
| твердий | рідкий | газ |
|---|---|---|
| 41 | 70 | 186 |
Гази, які служать ефективними транспортними засобами для поширення теплової енергії по великому об'єму простору, мають набагато вищі ентропії, ніж конденсовані фази. Аналогічно, рідини мають вищі ентропії, ніж тверді речовини, завдяки кратності способів взаємодії молекул (тобто накопичувати енергію).
Як ентропія залежить від концентрації
Оскільки речовина стає більш диспергованим у просторі, теплова енергія, яку вона несе, також поширюється на більший об'єм, що призводить до збільшення його ентропії. Оскільки ентропія, як і енергія, є великою властивістю, розбавлений розчин даної речовини цілком може володіти меншою ентропією, ніж той же обсяг більш концентрованого розчину, але ентропія на моль розчиненої речовини (молярна ентропія), звичайно, завжди буде збільшуватися як розчин стає більш розбавлений.
Для газоподібних речовин обсяг і тиск є відповідно прямими і зворотними показниками концентрації. Для ідеального газу, який розширюється при постійній температурі (це означає, що він поглинає тепло з навколишнього середовища, щоб компенсувати роботу, яку він виконує під час розширення), збільшення ентропії задається
\[ \Delta S = R \ln \left( \dfrac{V_2}{V_1} \right) \label{23.2.4}\]
Примітка: Якщо газу дозволяється охолонути під час розширення, співвідношення ускладнюється і найкраще буде обговорюватися в більш просунутому курсі.
Оскільки тиск газу обернено пропорційний його об'єму, ми можемо легко змінити вищевказане відношення, щоб висловити зміну ентропії, пов'язану зі зміною тиску ідеального газу:
\[ \Delta S = R \ln \left( \dfrac{P_1}{P_2} \right) \label{23.2.5}\]
Висловлюючи зміну ентропії безпосередньо в концентраціях, ми маємо аналогічне відношення
\[ \Delta S = R \ln \left( \dfrac{c_1}{c_2} \right) \label{23.2.6}\]
Хоча ці рівняння строго застосовуються тільки до досконалим газам і взагалі не можуть застосовуватися для рідин і твердих речовин, виявляється, що в розбавленому розчині розчинений розчин часто можна розглядати як газ, диспергований в обсязі розчину, тому останнє рівняння дійсно може дати досить точне значення для ентропії розведення розчину. Пізніше ми побачимо, що це має важливі наслідки при визначенні рівноважних концентрацій в однорідній реакційній суміші.
Як теплова енергія зберігається в молекулах
Теплова енергія - це частина енергії молекули, яка пропорційна її температурі, і, таким чином, відноситься до руху в молекулярному масштабі. Які види молекулярних рухів можливі? Для одноатомних молекул існує лише одне: фактичне переміщення з одного місця в інше, яке ми називаємо перекладом. Оскільки в просторі три напрямки, всі молекули володіють трьома режимами поступального руху.
Для багатоатомних молекул можливі два додаткових види рухів. Однією з них є обертання; лінійна молекула, така як CO 2, в якій всі атоми викладені вздовж осі x, може обертатися вздовж y- і z-осей, тоді як молекули, що мають меншу симетрію, можуть обертатися навколо всіх трьох осей. При цьому лінійні молекули мають два режими обертального руху, в той час як нелінійні мають три обертальні. Нарешті, молекули, що складаються з двох і більше атомів, можуть піддаватися внутрішнім коливанням. Для вільно рухаються молекул в газі кількість коливальних режимів або закономірностей залежить як від кількості атомів, так і від форми молекули, і вона швидко збільшується, оскільки молекула ускладнюється.
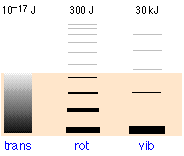
Відносні популяції квантованих станів поступальної, обертальної та коливальної енергій типової двоатомної молекули зображені товщиною ліній на цій схемі (не до масштабу!) діаграма. Кольорове затінення вказує на загальну теплову енергію, наявну при заданій температурі. Числа вгорі показують відстані порядку величини між сусідніми рівнями. Легко видно, що практично вся теплова енергія знаходиться в поступальних станах.
Зверніть увагу на різний інтервал трьох видів енергетичних рівнів. Це надзвичайно важливо, оскільки визначає кількість квантів енергії, які може прийняти молекула, і, як показано на наступній ілюстрації, кількість різних способів розподілу цієї енергії між молекулами.
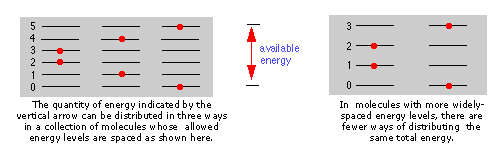
Чим ближче розташовані квантовані енергетичні стани молекули, тим більшою буде кількість способів, за допомогою яких задана кількість теплової енергії може бути розподілена між колекцією цих молекул.
Відстань між станами молекулярної енергії стає ближче в міру збільшення маси і кількості зв'язків в молекулі, тому можна взагалі сказати, що чим складніше молекула, тим більша щільність її енергетичних станів.
Квантові стани, мікростани та поширення енергії
На атомному і молекулярному рівні вся енергія квантована; кожна частинка володіє дискретними станами кінетичної енергії і здатна приймати теплову енергію тільки в пакетах, значення яких відповідають енергіям одного або декількох з цих станів. Багатоатомні молекули можуть зберігати енергію в обертальних і коливальних рухах, а всі молекули (навіть одноатомні) будуть володіти поступальною кінетичною енергією (тепловою енергією) при всіх температурах вище абсолютного нуля. Різниця енергій між сусідніми поступальними станами настільки хвилинна, що поступальну кінетичну енергію можна розглядати як безперервну (неквантовану) для більшості практичних цілей.
Кількість способів розподілу теплової енергії між дозволеними станами в межах колекції молекул легко обчислюється з простої статистики, але ми обмежимося прикладом тут. Припустимо, що у нас є система, що складається з трьох молекул і трьох квантів енергії, щоб поділитися між ними. Ми можемо віддати всю кінетичну енергію будь-якій одній молекулі, залишивши інші без жодної, ми можемо дати дві одиниці одній молекулі і одну одиницю іншій, або ми можемо розділити енергію порівну і дати одну одиницю кожній молекулі. Все сказане, існує десять можливих способів розподілу трьох одиниць енергії між трьома однаковими молекулами, як показано тут:

Кожна з цих десяти можливостей являє собою окремий мікростан, який опише систему в будь-який момент часу. Ті мікростану, які володіють однаковими розподілами енергії між доступними квантовими рівнями (і відрізняються лише тим, які саме молекули займають рівні) відомі як конфігурації. Оскільки всі мікростану однаково вірогідні, ймовірність будь-якої однієї конфігурації пропорційна кількості мікростанів, які можуть її виробляти. Таким чином, у наведеній вище системі конфігурація з маркуванням ii буде спостерігатися 60% часу, тоді як iii буде відбуватися лише 10% часу.
Зі збільшенням кількості молекул і кількості квантів кількість доступних мікростанів зростає вибухонебезпечно; якщо 1000 квантів енергії поділяють 1000 молекул, кількість доступних мікростанів буде близько 10 600 - число, яке значно перевищує кількість атомів у спостережуваному Всесвіт! Кількість можливих конфігурацій (як визначено вище) також збільшується, але таким чином, щоб значно знизити ймовірність всіх, крім найбільш ймовірних конфігурацій. Таким чином, для зразка газу, достатньо великого, щоб його можна було спостерігати в нормальних умовах, потрібно враховувати лише одну конфігурацію (розподіл енергії між квантовими станами); навіть другою найбільш ймовірною конфігурацією можна знехтувати.
Суть: будь-яка колекція молекул, досить великих за кількістю, щоб мати хімічне значення, матиме свою теплову енергію, розподілену по неймовірно великій кількості мікростанів. Кількість мікростанів збільшується експоненціально, оскільки більша кількість енергетичних станів («конфігурацій», як визначено вище) стає доступним завдяки
- Додавання квантів енергії (більш висока температура),
- Збільшення кількості молекул (в результаті дисоціації, наприклад).
- збільшується обсяг системи (що зменшує інтервал між енергетичними станами, дозволяючи заселятися більшій їх кількості при заданій температурі.
Тепло смерті: поширення енергії змінює світ
Енергія зберігається; якщо підняти книгу зі столу, і дати їй впасти, загальна кількість енергії в світі залишається незмінним. Все, що ви зробили, - це перенести його з форми, в якій вона зберігалася в глюкозі у вашому тілі, до ваших м'язів, а потім до книги (тобто ви працювали над книгою, перемістивши її вгору проти гравітаційного поля землі). Після того, як книга впала, існує така ж кількість енергії, як і теплова енергія (тепло) в книзі і стільниці.
Що змінилося, однак, - це доступність цієї енергії. Після того, як енергія поширилася на величезну кількість теплових мікростанів в розігрітих об'єктах, ймовірність її спонтанно (тобто випадково) стати нерозсіяною, по суті, дорівнює нулю. Таким чином, хоча енергія все ще «там», вона назавжди виходить за межі використання або відновлення. Глибина цього висновку була визнана приблизно в 1900 році, коли він вперше був описаний при «теплової смерті» світу. Мається на увазі те, що кожен спонтанний процес (по суті кожна зміна, що відбувається) супроводжується «розведенням» енергії. Очевидним наслідком є те, що вся кінетична енергія молекулярного рівня буде розподілена повністю, і більше нічого не станеться.
Чому гази мають тенденцію розширюватися, але ніколи не скорочуватися?
Всім відомо, що газ, якщо його залишити собі, буде прагнути розширюватися і заповнювати обсяг, в межах якого він обмежений повністю і рівномірно. Що «рухає» це розширення? На найпростішому рівні зрозуміло, що при більшій кількості вільного простору випадкові рухи окремих молекул неминуче розійдуть їх по всьому простору. Але як ми вже згадували вище, дозволені енергетичні стани, які можуть займати молекули, розташовані ближче в більшому обсязі, ніж в меншому. Чим більше обсяг, доступний газу, тим більшу кількість мікростанів може займати його теплова енергія. Оскільки всі подібні стани в межах термічно доступного діапазону енергій однаково вірогідні, розширення газу можна розглядати як наслідок тенденції теплової енергії поширюватися і розподілятися якомога ширше. Як тільки це сталося, ймовірність того, що цей розподіл енергії зміниться сам по собі (тобто, що газ спонтанно стиснеться), настільки хвилинна, щоб бути немислимою.

Уявіть собі газ, спочатку обмежений однією половиною коробки (рис.\(\PageIndex{7}\)). Потім бар'єр знімається, щоб він міг розширитися в повний обсяг ємності. Ми знаємо, що ентропія газу буде збільшуватися в міру поширення теплової енергії його молекул в збільшеному просторі. З точки зору поширення теплової енергії може бути корисним малюнок 23.2.X. Тенденція газу до розширення обумовлена більш близькими станами теплової енергії в більшому обсязі .
.

Ентропія змішування і розведення
Змішування та розведення дійсно означають одне і те ж, особливо для ідейних газів. Замініть пару контейнерів, показаних вище, на один, що містить два види молекул в окремих розділах (рис.\(\PageIndex{9}\)). Коли ми знімемо бар'єр, «червоні» і «сині» молекули будуть розширюватися в простір іншого. (Нагадаємо, Закон Далтона про те, що «кожен газ є вакуумом для іншого газу».) Однак зауважте, що хоча кожен газ зазнав розширення, загальний процес становить те, що ми називаємо «змішуванням».

Те, що вірно для газоподібних молекул, може, в принципі, стосуватися і розчинених в розчиннику молекул розчинених речовин. Але майте на увазі, що в той час як ентальпія, пов'язана з розширенням ідеального газу, за визначенням нуль, Δ H змішування двох рідин або розчинення розчиненої речовини в розчиннику мають кінцеві значення, які можуть обмежити змішуваність рідин або розчинність розчинної речовини. Але що дійсно драматично, так це те, що коли в ємність вводять лише одну молекулу другого газу (на малюнку\(\PageIndex{8}\)), стає можливим неймовірно величезна кількість нових конфігурацій, значно збільшуючи кількість мікростанів, які є термічно доступними (як зазначено по рожевому відтінку вище).
в ємність вводять лише одну молекулу другого газу (на малюнку\(\PageIndex{8}\)), стає можливим неймовірно величезна кількість нових конфігурацій, значно збільшуючи кількість мікростанів, які є термічно доступними (як зазначено по рожевому відтінку вище).
Чому тепло тече з гарячого в холодне
Подібно до того, як гази спонтанно змінюють свої обсяги від «меншого до більшого», потік тепла від більш теплого тіла до більш холодного завжди працює в напрямку «тепліше до охолоджувача», оскільки це дозволяє тепловій енергії заповнювати більшу кількість енергетичних мікростанів, оскільки нові стають доступними шляхом приведення більш прохолодний корпус контактує з теплим; по суті, теплова енергія стає більш «розбавленою».
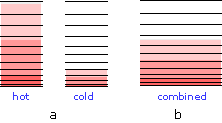
При введенні тіл в тепловий контакт (б) теплова енергія надходить з більш високих займаних рівнів в більш теплому об'єкті в незайняті рівні кулера до тих пір, поки в обох тілах не будуть зайняті рівні числа, доводячи їх до однакової температури. Як і слід було очікувати, збільшення кількості поширення та розподілу енергії пропорційно кількості тепла, що передається q, але є ще один фактор, який бере участь, і це температура, при якій відбувається передача. Коли кількість тепла q переходить в систему при температурі T, ступінь розрідження теплової енергії задається
\[\dfrac{q}{T}\]
Щоб зрозуміти, чому доводиться ділити на температуру, розглянемо вплив дуже великих і дуже малих значень T в знаменнику. Якщо організм, який отримує тепло, спочатку знаходиться при дуже низькій температурі, спочатку зайнято відносно мало станів теплової енергії, тому кількість енергії, що поширюється в вакантні стани, може бути дуже великим. І навпаки, якщо температура спочатку велика, всередині неї вже поширюється більше теплової енергії, і поглинання додаткової енергії матиме відносно невеликий вплив на ступінь теплового розладу всередині організму.
Хімічні реакції: чому постійна рівноваги залежить від температури
Коли відбувається хімічна реакція, беруть участь два види змін, що стосуються теплової енергії:
- Способи, якими теплова енергія може зберігатися в реагентах, як правило, відрізнятимуться від способів, пов'язаних з продуктами. Наприклад, в реакції H 2 → 2 H реагент дигідроген має коливальну і обертальну енергетичні стани, тоді як атомний водень в продукті має тільки поступальні стани— але загальна кількість поступальних станів у двох молів Н вдвічі більше, ніж в одному молі Н 2. . Через їх надзвичайно близький інтервал поступальні стани є єдиними, які дійсно враховуються при звичайних температурах, тому можна сказати, що теплова енергія може стати вдвічі розведеною («розкинутою») у продукті, ніж у реагенті. Якби це був єдиний фактор, який слід враховувати, то дисоціація диводню завжди була б спонтанною, і цієї молекули б не існувало.
- Однак для того, щоб ця дисоціація відбулася, кількість теплової енергії (тепла) q = Δ U повинна бути взята з оточення, щоб розірвати зв'язок H—H. Іншими словами, стан землі (енергія, при якій починається різноманіття енергетичних станів) вище в Н, про що вказує вертикальне зміщення правої половини в кожній з чотирьох панелей нижче.
На малюнку\(\PageIndex{11}\) а повторно схематичні зображення рівнів поступальної енергії двох компонентів H і H 2 реакції дисоціації водню. Затінення показує, як відносні популяції займаних мікростанів змінюються залежно від температури, внаслідок чого рівноважний склад змінюється на користь продукту дисоціації.
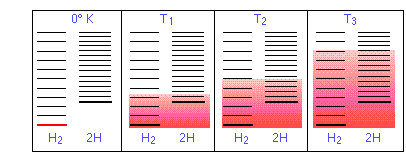
Здатність енергії поширюватися в молекули продукту обмежується наявністю достатньої теплової енергії для отримання цих молекул. Саме тут і надходить температура. При абсолютному нулі ситуація дуже проста; теплова енергія не доступна, щоб викликати дисоціацію, тому єдиним присутнім компонентом буде дигідроген.
- Зі збільшенням температури кількість заселених енергетичних станів зростає, про що вказує затінення на діаграмі. При температурі Т 1 число заселених станів Н 2 більше, ніж у 2Н, тому деякі з останніх будуть присутні в рівноважної суміші, але тільки як меншість компонента.
- При деякій температурі T 2 числа заселених станів в двох компонентах реакційної системи будуть ідентичними, тому рівноважна суміш буде містити Н 2 і «2Н» в рівних кількостях; тобто мольне співвідношення Н 2 /Н складе 1:2.
- Коли температура піднімається до T 3 і вище, ми бачимо, що кількість енергетичних станів, які є термічно доступними в продукті, починає перевищувати кількість для реагенту, тим самим сприяючи дисоціації.
Результат - саме те, що передбачає принцип Лешательє: рівноважний стан ендотермічної реакції зміщується вправо при більш високих температурах.
Наступна таблиця узагальнює ці відносини для чотирьох знакових комбінацій Δ H і Δ S. (Зверніть увагу, що використання стандартних значень Δ H° і Δ S° у прикладі реакцій не є суворо правильним тут і може дати оманливі результати при загальному використанні.)

Ця реакція горіння, як і більшість таких реакцій, є мимовільною при будь-яких температурах. Позитивна зміна ентропії обумовлена головним чином більшою масою молекул СО 2 порівняно з молекулами O 2.
< 0

- Δ Н° = -46,2 кДж
- Δ С° = —389 ДЖ К —1
- Δ G° = -16,4 кДж при 298 К
Зменшення молів газу в синтезі аміаку Хабера призводить до негативної зміни ентропії, роблячи реакцію спонтанною лише при низьких температурах. При цьому більш високий Т, який прискорює реакцію, також зменшує її протяжність.
> 0

- Δ Н° = 55,3 кДж
- Δ С° = +176 ДЖ К —1
- Δ G° = +2,8 кДж при 298 К
Реакції дисоціації, як правило, ендотермічні з позитивною зміною ентропії, і тому спонтанні при високих температурах. Зрештою, всі молекули розкладаються до своїх атомів при досить високих температурах.
< 0

- Δ Н° = 33,2 кДж
- ΔС° = —249 ДЖ, К — 1
- Δ G° = +51,3 кДж при 298 К
Ця реакція не є спонтанною при будь-якій температурі, а це означає, що її зворотний завжди спонтанний. Але оскільки зворотна реакція кінетично гальмується, NO 2 може існувати нескінченно довго при звичайних температурах, навіть якщо вона термодинамічно нестабільна.
фазові зміни
Всім відомо, що тверда речовина є стійкою формою речовини при низьких температурах, в той час як газоподібний стан переважає при високих температурах. Чому це повинно бути? Діаграма на малюнку\(\PageIndex{12}\) показує, що
- щільність енергетичних станів найменша в твердому тілі і найбільша (набагато, набагато більше) в газі, а
- наземні стани рідини і газу компенсуються від попереднього стану теплом плавлення і випаровування відповідно.

Зміни фази передбачають обмін енергією з оточенням (енергетичний вміст якого щодо системи вказано (з великим перебільшенням!) по висоті жовтих вертикальних смуг на рис\(\PageIndex{13}\). Коли тверде тіло і рідина знаходяться в рівновазі (середній розділ діаграми нижче), є достатня теплова енергія (позначена рожевим затіненням) для заповнення енергетичних станів обох фаз. Якщо тепло дозволяється надходити в навколишнє середовище, воно вибірково виводиться з більш рясно заселених рівнів рідкої фази, внаслідок чого кількість цієї фази зменшується на користь твердої речовини. Температура залишається постійною, оскільки тепло плавлення повертається в систему в точній компенсації тепла, втраченого в навколишнє середовище. Нарешті, після того, як останній слід рідини зник, єдиними залишеними станами є тверде тіло. Будь-яке подальше відведення тепла призводить до зниження температури, оскільки стани твердого тіла знежирюються.

Колігативні властивості розчинів
Зниження тиску пари, підвищення температури кипіння, депресія температури замерзання та осмос - відомі явища, які виникають, коли нелеткі розчинені речовини, такі як цукор або сіль, розчиняються в леткому розчиннику, такому як вода. Всі ці ефекти виникають внаслідок «розведення» розчинника доданою розчиненою речовиною, і через цю спільність їх відносять до колігативних властивостей (лат. з лігаром, підключений до.) Ключова роль концентрації розчинника прихована значно спрощеними виразами, що використовуються для обчислення величини цих ефектів, в яких з'являється лише концентрація розчиненої речовини. Деталі того, як проводити ці розрахунки та багато важливих застосувань колігативних властивостей, розглядаються в інших місцях. Наша мета тут - запропонувати більш повне пояснення того, чому відбуваються ці явища.
В основному, все це є результатом впливу розведення розчинника на його ентропію, а отже, збільшення щільності енергетичних станів системи в розчині в порівнянні з такою в чистій рідині. Рівновага між двома фазами (рідина-газ для кипіння і тверда рідина для заморожування) виникає, коли енергетичні стани в кожній фазі можуть бути заселені з однаковою щільністю. Температури, при яких це відбувається, зображуються затіненням.

Розведення розчинника додає рідини нові енергетичні стани, але не впливає на парову фазу. Це підвищує температуру, необхідну для того, щоб зробити рівну кількість мікростанів доступними в двох фазах.

Розведення розчинника додає рідини нові енергетичні стани, але не впливає на тверду фазу. Це знижує температуру, необхідну для того, щоб зробити рівну кількість станів доступними в двох фазах.
Вплив тиску на ентропію: Осмотичний тиск
Коли рідина піддається гідростатичному тиску - наприклад, інертним, що не розчиняється газом, який займає паровий простір над поверхнею, тиск пари рідини підвищується (рис.\(\PageIndex{16}\)). Тиск діє на стиснення рідини дуже незначно, ефективно звужуючи потенційну енергетичну свердловину, в якій проживають окремі молекули, і тим самим збільшуючи їх схильність до виходу з рідкої фази. (Оскільки рідини не дуже стисливі, ефект досить малий; застосований тиск 100 атм підніме тиск пари води при 25° C лише приблизно на 2 торр.) З точки зору ентропії можна сказати, що прикладається тиск зменшує розміри «коробки», всередині якої основні поступальні рухи молекул обмежені всередині рідини, тим самим знижуючи щільність енергетичних станів в рідкій фазі.

Застосування гідростатичного тиску до рідини збільшує відстань її мікростанів, так що кількість енергетично доступних станів в газі, хоча і незмінних, є відносно більшою - тим самим збільшуючи тенденцію молекул до виходу в парову фазу. Що стосується вільної енергії, то більш високий тиск підвищує вільну енергію рідини, але не впливає на енергію газової фази.

Цим явищем можна пояснити осмотичний тиск. Осмотичний тиск, слід нагадати студентам, - це не те, що рухає осмосом, а, скоріше, гідростатичний тиск, який необхідно застосовувати до більш концентрованого розчину (більш розбавленого розчинника), щоб зупинити осмотичний потік розчинника в розчин. Ефект цього тиску\(\Pi\) полягає в тому, щоб трохи збільшити відстань між енергетичними станами розчинника на стороні мембрани високого тиску (розбавлений розчинник), щоб відповідати рівновазі чистого розчинника, відновлюючи осмотичну рівновагу.
