4.7: Моделювання експозиції
- Page ID
- 18331
3.8. Моделювання експозиції
3.8.1. Як оцінити викиди?
У підготовці
3.8.2. Мультікамерне моделювання
Автори: Дік ван де Меент та Майкл Меттіс
Рецензент: Джон Парсонс
Цілі навчання:
Ви повинні вміти
- пояснити, що таке рівняння балансу маси
- опишіть, як рівняння балансу маси використовуються в мультимедійному моделюванні до
- пояснити поняття термодинамічної рівноваги і сталого стану
- наведіть кілька прикладів використання мультимедійного моделювання балансу маси
Ключові слова: модель природоохоронної долі, рівняння балансу маси
Рівняння балансу маси
Багатокамерне (або мультимедійне) моделювання балансу маси починається з універсального принципу збереження, сформульованого як рівняння балансу. Керівний принцип полягає в тому, що швидкість зміни (будь-якої сутності, у будь-якій системі) дорівнює різниці між сумою всіх входів (цієї сутності) до системи та сумою всіх виходів з неї. Екологічні моделісти використовують рівняння балансу для прогнозування концентрацій впливу хімічних речовин у навколишньому середовищі шляхом вирахування зі знань про швидкість вхідних і вихідних процесів, що можна зрозуміти найпростіше з розгляду рівняння балансу маси для одного єдиного екологічного відсіку (рис. 1) :
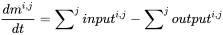(ур. 1)
де d m i, j /d t являє собою зміну маси хімічної речовини i в відсіку j (кг) з плином часу (s), а вхід i, j і вихід i, j позначають швидкості введення і виведення хімічної речовини в і з відсіку j відповідно.
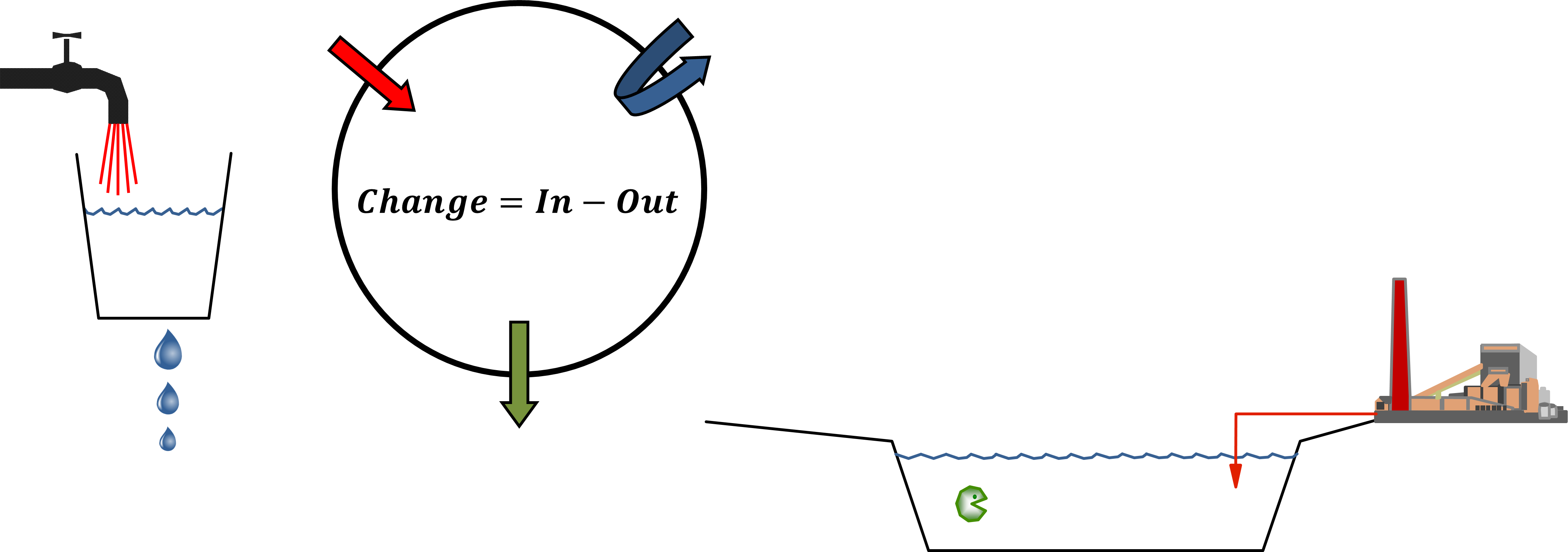
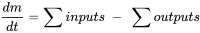.Модель з одним купе
У мультимедійному моделюванні балансу маси формулюються рівняння балансу маси (типу, показаного в рівнянні 1) для кожного екологічного відсіку. Відтоки хімічної речовини з відсіків часто пропорційні кількості хімічної речовини, присутньої в відсіках, тоді як зовнішні входи (викиди) часто можна вважати постійними. У таких випадках, тобто при застосуванні кінетики першого порядку (див. Розділ 3.3 про екологічну долю хімічних речовин), рівняння балансу маси приймають форму рівняння 1 розділу 3.3. Тільки для одного відсіку (наприклад, озера, як на рис. 1):
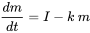(ур. 2)
в якому d m /d t (кг.с -1) - швидкість зміни маси (кг) хімічної речовини в озері, I (кг.с -1) - (постійна) швидкість викиду, а твір k. m (kg.s -1) позначає швидкість втрати хімічної речовини першого порядку з озера. Очевидно, що з часом повинен розвинутися стійкий стан, при якому маса хімічної речовини в озері досягає передбачуваного максимуму.
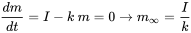(ур. 2а)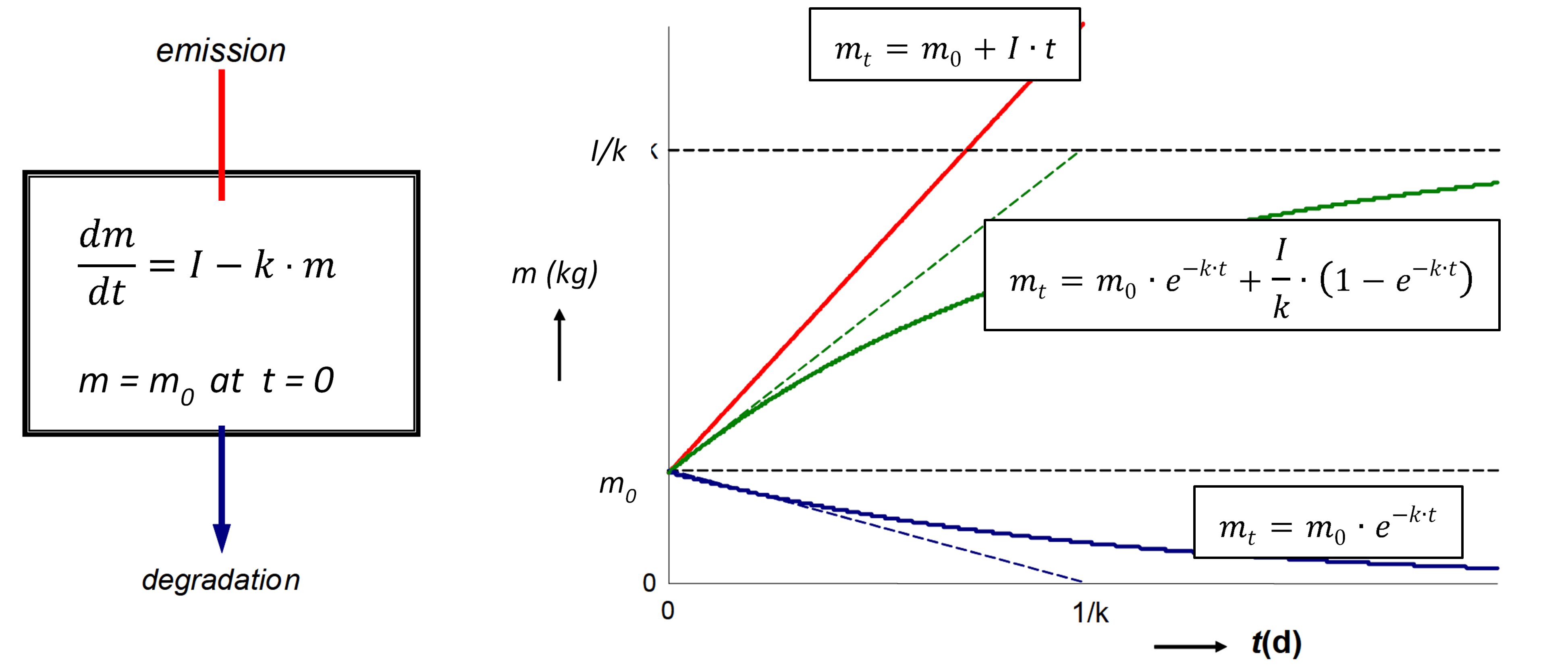
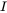, який буде досягнутий при нескінченний час 
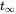. Після Ван де Меент та ін. (2011). 
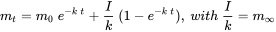(ур. 3)
Коли вхідна швидкість (емісія) постійна, тобто що вона не змінюється з часом, і не залежить від маси присутніх хімічних речовин, маса хімічної речовини в системах, як очікується, збільшиться в геометричній прогресії, від початкового значення при
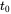, до стійкого рівня на 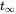. Згідно з рівнянням 3, слід очікувати кінцевого рівня маси, рівного.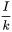 
Модель з декількома відсіками
Префікс 'multi' вказує на те, що зазвичай (багато) розглядається більше одного екологічного відсіку. Unit World (див. Нижче) містить повітря, воду, біоту, осад і ґрунт; більш досконалі глобальні системи моделювання можуть використовувати сотні відсіків. Корпус трьох відсіків (зазвичай один повітряний, один водяний, один грунт) схематично опрацьований на малюнку 3.
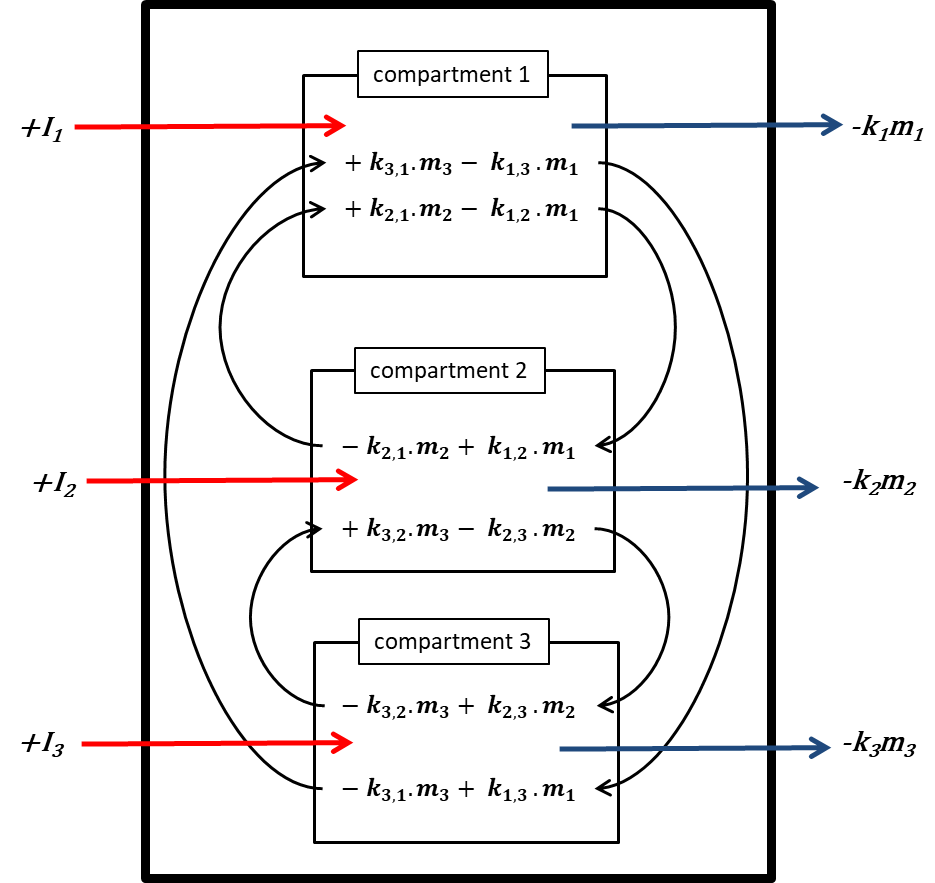
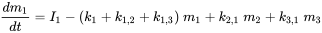
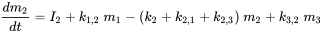
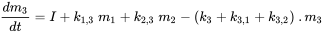
Кожен відсік може отримувати постійні входи (викиди, імпорт), а хімічні речовини можуть експортуватися з кожного відсіку шляхом деградації або адвективного відтоку, як в однокамерній моделі. Крім того, хімічні речовини можуть перевозитися між відсіками (одночасний імпорт-експорт). Всі масові потоки характеризуються (псевдо-) константами швидкості першого порядку (див. Розділ 3.3 про процеси природоохоронної долі). Три рівняння балансу маси в кінцевому підсумку балансують до нуля в нескінченний час:
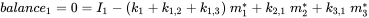
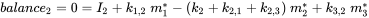
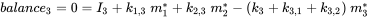(ур. 4)
де символи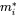 
позначають масу в відсіках i в сталому стані. Множини n лінійних рівнянь з n невідомими можуть бути вирішені алгебраїчно, вручну маніпулюючи рівняннями 4, поки не будуть отримані чисті вирази для кожного з трьох m i значень, що неминуче стає нудним, як тільки потрібно вирішити більше двох рівнянь балансу маси - це не утримав одного з найвідоміших аспірантів професора Маккея від успішного вирішення набору з 14 рівнянь! Більш простий спосіб розв'язання множин n лінійних рівнянь з n невідомими є за допомогою лінійної алгебри. Використовуючи лінійне алгебраїчне векторно-матричне числення, рівняння 4 можна переписати в одне лінійно-алгебраїчне рівняння:
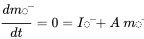(ур. 5)
в якому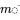 
знаходиться вектор мас в трьох відсіках, 
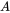являє собою модельну матрицю відомих швидкісних констант і 
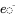є вектором відомих швидкостей викидів:
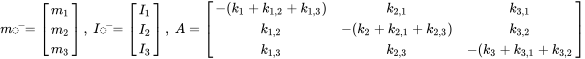
Розв'язок рівняння 5 дорівнює
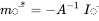
в якому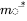 
є вектором мас при сталому стані і 
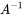є оберненою матрицею моделі 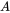. Лінійний алгебраїчний метод розв'язання лінійних рівнянь балансу маси легко переноситься за допомогою програмного забезпечення електронних таблиць (наприклад MS Excel, LibreOffice Calc або Google Sheets), які містять вбудовані функції масиву для інвертування матриць і множення їх на вектори.
Підрозділ Світ моделювання
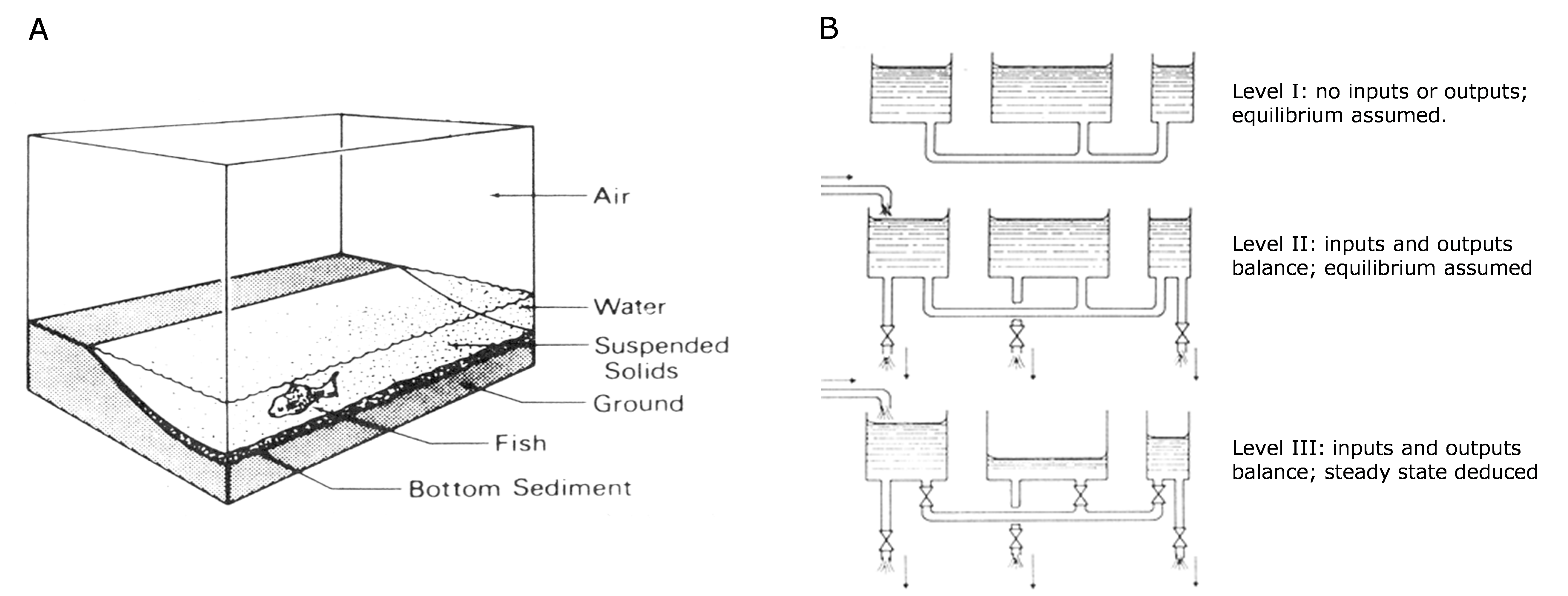
Наприкінці 1970-х років новаторські вчені-екологи Лабораторії екологічних досліджень USEPA в Афіні, GA, визнали, що універсальне (масове) рівняння балансу, застосоване до відсіків екологічних середовищ (повітря, вода, біота, осад, ґрунт) може служити засобом для аналізу та розуміння відмінностей в екологічній поведінці і долі хімічних речовин. Їх «оцінювальний Unit World Modeling» (Baughman and Lassiter, 1978; Neely and Blau, 1985) став початком того, що зараз відомо як мультимедійне моделювання балансу маси. Концепція Unit World була розроблена та відшліфована Маккеєм та колегами (Нілі та Маккей, 1982; Маккей і Патерсон, 1982; Маккей та співавт., 1985; Патерсон і Маккей, 1985, 1989). У моделюванні Unit World навколишнє середовище розглядається як сукупність добре змішаних хімічних реакторів, кожен з яких представляє одне середовище навколишнього середовища (відсік), до і з якого хімічні потоки, керовані «відходом від рівноваги» - це хімічна технологія жаргону для вираження ступеня, до якої термодинамічний Рівноважні властивості, такі як «хімічний потенціал» або «нечіткість», відрізняються (рис. 4). Маккей та колеги використовували fugacity у моделюванні балансу маси як центральну змінну стану. Незабаром після публікації цього «підходу до невимушеності» (Mackay, 1991) термін «модель невимушеності» став широко використовуватися для назви всіх моделей «типу Маккея», який застосовував «Unit World моделювання балансу маси», хоча більшість цих моделей продовжували використовувати більш традиційну хімічну масу як змінну стану.
Рівні складності
Хоча концептуально простий (екологічна доля схожа на витікання ковша, в тому сенсі, що його стабільна висота води передбачувана з кінетики першого порядку), динамічний характер моделювання балансу маси часто не настільки інтуїтивно зрозумілий. Абстрактна математична перспектива може найкращим чином пояснити моделювання балансу маси, але це може бути не практичним для всіх студентів. У своїй книзі про мультимедійне моделювання балансу маси Маккей вирішив навчити своїх учнів інтуїтивному підходу за допомогою своєї знаменитої аналогії з резервуаром для води (рис. 4B).
Відповідно до цього інтуїтивного підходу, моделювання балансу маси можна проводити на рівнях зростаючої складності, де найнижчий, найпростіший рівень, який служить меті, повинен розглядатися як найбільш підходящий. Найменш складним є рівень I, який передбачає відсутність входу та виходу. Хімічна речовина може вільно (тобто без обмежень) перетікати з одного екологічного відсіку в інший, поки не досягне свого стану найнижчої енергії: стану термодинамічної рівноваги. У такому стані хімічна речовина має рівний хімічний потенціал і неміцність у всіх середовищах навколишнього середовища. Система знаходиться в стані спокою; за гідравлічною аналогією вода має рівні рівні у всіх резервуарах. Це найнижчий рівень складності моделі, оскільки ця модель вимагає лише знання кількох термодинамічних констант рівноваги, що можна аргументувати з основних властивостей фізичної речовини.
Більш складний рівень моделювання III описує середовище, в якому потік хімічної речовини між відсіками відчуває опір потоку, так що стійкий стан балансу між виходами і входами досягається лише ціною постійного «відходу від рівноваги». Також розглядаються деградація у всіх відсіках та адвективні потоки, наприклад, падіння дощу або вітрові та водні течії. Сталий стан III рівня - це той, при якому неміцності хімічної речовини в відсіках нерівні (немає термодинамічної рівноваги); в гідравлічній аналогії вода в баках відпочиває на різній висоті. Природно, що рішення рівня моделювання III вимагає детального знання входів (в який відсік (и) викидається хімічна речовина?) , Виходи (з якими темпами хімічна деградація в різних відсіках?) і опори перенесення (наскільки швидким або повільним є перенесення маси між різними відсіками?). Моделісти рівня III отримують винагороду за це, отримуючи більш реалістичні результати моделі.
Четвертий комплексний рівень мультимедійного моделювання балансу маси (рівень IV, не показаний на малюнку 4В) створює перехідні (залежні від часу) рішення. Модельне моделювання починається (t = 0) з нульовим хімічним (m = 0; порожні резервуари для води). Відсіки (резервуари), заповнюються поступово, поки система не прийде в сталий стан, в якому зазвичай один або кілька відсіків відходять від рівноваги, як при моделюванні III рівня. Рівень IV є найбільш реалістичним відображенням екологічної долі хімічних речовин, але вимагає найбільш детальних знань про масові потоки та опори масоперенесення. Більш того, змінні в часі стани найменш легко інтерпретувати і не завжди найбільш інформативні хімічної долі. Найважливішою інформацією, яку слід отримати від моделювання рівня IV, є вказівка часу на сталий стан: скільки часу потрібно, щоб очистити навколишнє середовище від стійких хімічних речовин, які більше не використовуються?
Маккей описує проміжний рівень складності (рівень II), при якому виходи (деградація, адвективні відтоки) балансують входи (як на рівні III), а хімічні дозволяється вільно протікати між відсіками (як на рівні I). Сталий стан розвивається на рівні II і постійно існує термодинамічна рівновага. Моделювання на рівні II не вимагає знання опорів масоперенесення (крім цього опори незначні!) , але темпи деградації та відтоку збільшують складність моделі порівняно з рівнем I. У багатьох ситуаціях моделювання рівня II дає напрочуд реалістичні результати.
Використання мультимедійних моделей балансу маси
Незабаром після публікації першого використання «оцінювального моделювання Unit World» (Mackay and Paterson, 1982) почали з'являтися специфічні застосування «Маккейського підходу» до мультимедійного моделювання балансу маси. Група Mackay опублікувала кілька моделей для оцінки хімічних речовин в Канаді, з яких ChemCan (Mackay et al., 1995) відомий найбільше. Ще до ChemCan вийшли каліфорнійська модель CalTox (Mckone, 1993) та голландська модель SimpleBox (Van de Meent, 1993) з подальшою публікацією моделі HAZCHEM Європейським центром екотоксикології та токсикології хімічних речовин (ECETOC, 1994) та німецької моделі Umwelt Bundesamt ELPOS (Beyer and Меттіс, 2002). По суті, всі ці моделі служать тій самій меті, що і оригінальна модель Unit World, а саме надання стандартизованих платформ моделювання для оцінки можливих екологічних ризиків від соціального використання хімічних речовин.
Мультимедійні моделі балансу маси стали важливим інструментом у прийнятті нормативних екологічних рішень щодо хімічних речовин. У Європі хімічні речовини можуть бути зареєстровані для збуту відповідно до регламенту REACH лише тоді, коли буде продемонстровано, що хімічна речовина може бути використана безпечно. Важливу роль у реєстрації відіграє мультимедійне моделювання балансу маси за допомогою SimpleBox (Hollander et al., 2014) та SimpleTreat (Struijs et al., 2016).
Хоча ранні мультимедійні моделі балансу маси пішли по стопах концепції Mackay Unit World (приймаючи сталий підхід і використовуючи один відсік на навколишнє середовище), пізніші моделі стали більшими, просторово і тимчасово явними, і були використані для поглибленого аналізу хімічної долі.
Наприкінці 1990-х років Ваня та його колеги розробили глобальну модель розподілу стійких органічних забруднювачів (GloboPop). Вони використовували свою глобальну мультимедійну модель балансу маси для дослідження так званого ефекту холодної конденсації, за допомогою якого вони пояснили виникнення відносно великої кількості стійких органічних хімічних речовин в Арктиці, де їх ніхто ніколи не використовував (Wania, 1999). Шерінгер та колеги використовували свою модель ClimoChem для дослідження переносу стійких хімічних речовин на великі відстані в альпійські регіони (Scheringer, 1996; Wegmann et al., 2005). MacLeod та колеги (Toose et al., 2004) побудували глобальну мультимедійну модель балансу маси (BETR World) для вивчення глобального переносу забруднюючих речовин на великі відстані.
Посилання
Бойман, Г.Л., Ласситер, Р. (1978). Прогнози концентрацій забруднюючих речовин навколишнього середовища. В: Оцінка небезпеки хімічних речовин для водного життя. АСТМ СТП 657, с. 35-54.
Байєр, А., Меттіс М. (2002). Критерії атмосферного переносного потенціалу та стійкості пестицидів та промислових хімічних речовин. Умвельтбундесамт Беріхте 7/2002, Е. Шмідт-Верлаг, Берлін. ІСБН 3-503-06685-3.
ЕКЕТОК (1994). HAZCHEM, Математична модель для використання в оцінці ризику речовин. Європейський центр екотоксикології та токсикології хімічних речовин, Брюссель.
Холландер, А., Schoorl, М., Ван де Меент, Д. SimpleBox 4.0: Поліпшення моделі, зберігаючи її простою... Хемосфера 148, 99-107.
Маккей, Д. (1991). Мультимедійні моделі екологічної долі: підхід Fugacity. Льюїс Видавці, Челсі, Мічиган
Маккей, Д., Патерсон С. Розрахунок неміцності. Екологічна наука і технологія 16, 274-278.
Маккей, Д., Патерсон, С., Чунг, Б., Нілі, В.Б. (1985). Оцінка екологічної поведінки хімічних речовин за допомогою моделі неміцності III рівня. Хемосфера 14, 335-374.
Маккей, Д., Патерсон, С., Там, Д.Д., Ді Гвардо, А., Кейн, Д. (1995). ChemCan: Регіональна модель незахищеності рівня III для оцінки хімічної долі в Канаді. Екологічна токсикологія та хімія 15, 1638-1648.
Макконе, Т.Є. CALTOX, мультимедійна модель загального впливу для небезпечних відходів сайтів. Національна лабораторія Лоуренса Лівермора. Лівермор, Каліфорнія.
Нілі, В.Б., Блау, Г.Є. Вступ до впливу хімічних речовин. В: Нілі, В.Б., Блау, Г.Є. (ред.). Навколишнє середовище від хімічних речовин Том I, CRC Прес, Бока-Ратон, Флорида, стор 1-10.
Нілі, В.Б., Маккей, Д. (1982). Оцінювальна модель оцінки екологічної долі. В: Моделювання долі хімічних речовин у водному середовищі. Енн-Арбор Наука, Енн-Арбор, Мічиган, стор. 127-144.
Патерсон С. Моделі рівноваги для початкового інтегрування фізико-хімічних властивостей. В: Нілі, В.Б., Блау, Г.Є. (ред.). Вплив на навколишнє середовище від хімічних речовин Том I, CRC Press, Бока-Ратон, Флорида, стор 218-231.
Патерсон С., Маккей Д. Модель, що ілюструє екологічну долю, вплив та поглинання людиною стійких органічних хімічних речовин. Екологічне моделювання 47, 85-114.
Шерінгер, М. Стійкість та просторовий діапазон як кінцеві точки оцінки органічних хімічних речовин на основі впливу. Екологічна наука і технологія 30, 1652-1659.
Струйс, Дж., Ван де Меент, Д., Шованек, Д., Бухгольц, Х., Пату, Р., Вольф, Т., Остін, Т., Толлс, Дж., Ван Леувен, К., Галай-Бургос, М. (2016). Адаптація SimpleTreat для моделювання поведінки хімічних речовин під час очищення промислових стічних вод. Хемосфера 159:619-627.
Туз, Л., Вудфайн, Д.Г., Маклауд, М., Маккей, Д., Гуін, Дж. (2004). Бетр-світ: географічно явна модель хімічної долі: застосування для транспортування альфа-ГХГ до забруднення навколишнього середовища Арктики 128, 223-40.
Ван де Меент Д. (1993). SimpleBox: Загальна мультимедійна модель оцінки долі. Національний інститут охорони здоров'я та навколишнього середовища. Звіт РВМ 672720 001. Білтховен, Н.Л.
Ван де Меент, Д., МакКоне, Т.Е., Паркертон, Т., Меттіс, М., Шерінгер, М., Ваня, Ф., Перді, Р., Беннетт, Д. (2000). Стійкість та транспортний потенціал хімічних речовин у мультимедійному середовищі. В: Клецька, г. та ін. (ред.) Оцінка стійкості та переносного потенціалу органічних хімічних речовин у довкіллі. Преса SETAC, Пенсакола FL, глава 5, стор. 169-204.
Ван де Меент, Д., Холландер, А., Пайненбург, В., Брейр, Т. Доля і транспортування забруднень. В: Санчес-Байо, Ф., Ван ден Брінк, П.Дж., Манн, Р.М. (ред.) , Екологічний вплив токсичних хімічних речовин, Bentham Science Publishers, стор. 13-42.
Ваня, Ф. (1999). Про походження підвищеного рівня стійких хімічних речовин в навколишньому середовищі. Наука про навколишнє середовище та дослідження забруднення 6, 11-19.
Вегман, Ф., Шерінгер, М., Хунгербюлер, К. Перші дослідження впливу гірської холодної конденсації за допомогою моделі ClimoChem. Екотоксикологія та екологічна безпека 63, 42-51.
Опишіть, використовуючи власні слова, істотні характеристики рівнянь балансу маси.
Що таке «сталий стан»? Що таке «рівновага»? Використовуйте кілька рядків тексту, щоб описати найнеобхідніше, вказавши відмінності та спільні риси.
Рівняння балансу маси використовуються в моделями для розрахунку концентрацій речовин в навколишньому середовищі, враховуючи знання про норми викидів. Наведіть відпрацьований приклад для ситуації з одним відсіком, наприклад, прісноводного озера.
Назвіть та опишіть один (або декілька) прикладів мультимедійного моделювання балансу маси.
3.8.3. Моделі металевих видів
Автори: Вілько Вервей
Рецензенти: Джон Парсонс, Стівен Лофтс
Цілі навчання:
Ви повинні вміти
- Розуміти основи моделювання видоутворення
- Зрозумійте фактори, що визначають видоутворення та способи їх обчислення
- Зрозумійте, в яких типах ситуацій моделювання видоутворення може бути корисним
Ключові слова: видоутворення, розчинність, органічне комплексоутворення
Вступ
Моделі видоутворення дозволяють користувачам розраховувати видоутворення розчину, а не вимірювати його хімічним способом або оцінювати його опосередковано за допомогою біоаналізів (див. Розділ 3.5). Як правило, моделі видоутворення приймають загальні концентрації як вхідні дані та обчислюють видові концентрації.
Моделі видоутворення використовують термодинамічні дані про хімічні рівноваги для розрахунку видоутворення. Ці дані, виражені у вільній енергії або у вигляді констант рівноваги, можна знайти в літературі. Термін «константа» трохи вводить в оману, оскільки константи рівноваги залежать від температури та іонної сили розчину. Іонна сила розраховується з концентрацій (С) і зарядів (Z) іонів в розчині за допомогою рівняння:
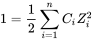
Для багатьох рівноваг немає інформації для корекції температури. Для корекції іонної сили доступно безліч напівемпіричних методів, жоден з яких не є ідеальним.
Як працюють ці моделі
Для кожної реакції рівноваги може бути визначена постійна рівноваги. Наприклад, за реакцію
Cu 2+ 4 Сл - КуСл 4 2-
константу рівноваги можна визначити як
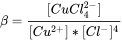
Отже, коли відомі концентрації вільних Cu 2+ і вільного Cl -, концентрацію CuCl 4 2- можна легко розрахувати як:
[CuCl 4 2-] = β * [Cu 2+] * [Кл -] 4
Насправді концентрації вільних Cu 2+ та вільного Cl - часто НЕ відомі, але відомі загальні концентрації Cu та Cl в системі. Для того, щоб знайти видобуток, нам потрібно налаштувати набір рівнянь балансу маси, наприклад:
[загальний Cu] = [вільний Cu 2+] + [CuOH +] + [Cu (OH) 2] + [Cu (OH) 3 -] (..) + [CuCl +] + [CuCl 2] (..) і т.д.
[загальна Cl] = (..)
Кожна концентрація комплексу є функцією вільних концентрацій іонів, що входять до його складу. Таким чином, ми можемо сказати, що якщо ми знаємо концентрації всіх вільних іонів, ми можемо обчислити концентрації всіх комплексів, а потім ми можемо обчислити загальні концентрації. Рішення задачі неможливо знайти шляхом перестановки рівнянь балансу мас, оскільки вони є нелінійними. Модель видоутворення полягає в тому, щоб багаторазово оцінювати концентрації вільних іонів, на кожному циклі коригуючи їх так, щоб розраховані загальні концентрації більш точно відповідали відомим підсумкам. Коли розраховані та відомі загальні концентрації всі узгоджуються з певною точністю, видоутворення було розраховано. Важливою частиною розрахунку є коригування концентрацій вільних іонів розумним та ефективним способом, щоб якомога швидше знайти рішення. Для вирішення цього є кілька більш-менш складних методів, але зазвичай застосовується метод Ньютона-Рафсона.
Вплив температури і іонної сили
Насправді пояснення вище занадто просте. Константи Equilbrium дійсні в конкретних умовах для температури та іонної сили (наприклад, стандартні умови 25 o C і [endif] —> і повинні бути перетворені в температуру та іонну силу системи, для якої обчислюється видобуток. Можна адаптувати константи рівноваги для нестандартних температур, але для цього потрібно знання даних теплоємності (ΔH) кожної рівноваги. Ці знання часто недоступні. Константи можна перетворити від 25° C до інших температур за допомогою рівняння Ван Гофа:
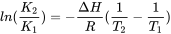
де K 1 і K 2 - константи, T 1 і T 2 температури, Δ H - ентальпія реакції і R - газова константа.
Константи рівноправності також дійсні для одного конкретного значення іонної сили. Для перетворення з одного значення іонної сили в інше може використовуватися безліч різних підходів. Ця конверсія є досить важливою, оскільки вже при відносно низьких іонних силах відхилення від ідеальності стають значними, і активність виду починає відхилятися від його концентрації. Отже, внутрішні, або термодинамічні, константи рівноваги (тобто константи при гіпотетичній іонній силі нуля) вже не діють і активність а іонів при ненульовій іонній силі потрібно розраховувати з концентрації та коефіцієнта активності:
а = γ * с
де γ - коефіцієнт активності (безрозмірний; іноді ще називають f) і c - концентрація; а і с знаходяться в моль/літр.
Перше рішення для розрахунку коефіцієнтів активності для ненульової іонної сили було запропоновано Дебаєм і Хюкелем в 1923 році. Теорія Дебея-Хюкеля передбачає, що іони є точковими зарядами, тому вона не враховує обсяг, який займають ці іони, ні об'єм оболонки лігандів та/або молекул води навколо них. Debye-Hückel дає хороші наближення, до приблизно 0,01 М для 1:1 -електроліту, але лише до близько 0,001 М для електроліту 2:2. Коли іонна сила перевищує ці значення, коефіцієнти активності, які прогнозує наближення Дебея-Хюкеля, значно відхиляються від експериментальних значень. Багато екологічних застосувань вимагають перетворення для більш високих іонних сильних сторін, що робить рівняння Дебея-Гюккеля недостатнім. Щоб подолати цю проблему, багато дослідників запропонували інші методи, такі як розширене рівняння Дебе - Гюккеля, рівняння Гюнтельберга та рівняння Девіса, а також рівняння Бромлі, рівняння Пітцера та теорія конкретної взаємодії іонів (SIT).
Багато програм використовують рівняння Девіса, яке обчислює коефіцієнти активності γ наступним чином:
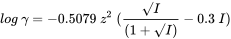
де z - заряд виду, а I - іонна сила. Іноді використовується 0,2 замість 0,3. В основному всі ці підходи приймають рівняння Дебія-Гюкеля як відправну точку і додають один або кілька термінів для виправлення відхилень при більш високих іонних силах. Хоча багато хто з цих методів здатні досить добре передбачити активність іонів, насправді вони є переважно емпіричними розширеннями без міцної теоретичної основи.
Розчинність
Більшість солей мають обмежену розчинність; в декількох випадках розчинність також важлива в умовах, що відбуваються в навколишньому середовищі. Наприклад, для CaCo 3 продукт розчинності становить 10 -8,48, що означає, що коли [Ca 2+] * [CO 3 2-] > 10 -8,48, CaCo 3 випаде в осад, поки [Ca 2+] * [CO 3 2-] = 10 -8 4.8. Але це також працює навпаки: якщо твердий CaCo 3 присутній у розчині, де [Ca 2+] * [CO 3 2-] < 10 -8.48 (зверніть увагу на знак «<'--), твердий CaCo 3 розчиниться, поки [Ca 2+] * [CO 3] 2-] = 10 -8.48. Зверніть увагу, що Ca і CO 3 у формулі тут відносяться до вільних іонів. Наприклад, 10 -13 М розчин Ag 2 S призведе до осадження Ag 2 S. Вільні концентрації Ag і S становлять 6,5*10 -15 М і 1,8*10 -22 М відповідно. (Що відповідає продукту розчинності 10 -50.12, але розчинені концентрації Ag і S становлять 7,1*10 -15 М і 3,6*10 -15 М відповідно, тому для S на сім порядку вище. Це обумовлено утворенням S-комплексів з протонами (HS - і H 2 S (aq)) і в меншій мірі з Ag.
Комплексоутворення органікою
Комплексоутворення з розчиненим органічним вуглецем (DOC) відрізняється від неорганічного комплексоутворення або комплексоутворення з чітко визначеними сполуками, такими як ацетат або NTA. Причини такої різниці полягають у наступному.
- DOC дуже неоднорідний; DOC, ізольований на двох ділянках, може сильно відрізнятися (не кажучи вже про складність вибору процедур ізоляції).
- Комплексоутворення з DOC зазвичай показує безперервний діапазон рівноважних констант через хімічні та стеричні відмінності в сусідніх групах.
- Підвищення катіонного зв'язування і/або іонна сила розчину змінюють електростатичні взаємодії між функціональними групами в DOC-молекулах, що впливає на константи рівноваги.
- Крім того, зміна електростатичних взаємодій може спричинити конформаційні зміни молекул.
Серед найпопулярніших моделей для оцінки органічного комплексоутворення - Модель V (1992), VI (1998) та VII (2011), також відома як WHAM, написана Чайовими та співавторами (Tipping & Hurley, 1992; Чайові, 1994, 1998; Чайові, Лофти та Сонке, 2011). Всі ці моделі припускають, що відбувається два види зв'язування: специфічне зв'язування і накопичення в дифузному подвійному шарі. Специфічне зв'язування - це утворення хімічного зв'язку між іоном і функціональною групою (або групами) на органічній молекулі. Дифузне двошарове накопичення - це накопичення іонів протилежного електричного заряду, прилеглих до молекули, без утворення хімічного зв'язку (електричний заряд зазвичай негативний, тому іони, які накопичуються, є катіонами).
Для специфічного зв'язування всі ці моделі розрізняють фульвокислоти (ФА) і гумінові кислоти (ГК), які обробляються окремо. Ці два класи DOC, як правило, є найпоширенішими компонентами природних органічних речовин у навколишньому середовищі - у поверхневих прісних водах фульвокислоти, як правило, найбільш поширені. Для кожного класу в моделі використовується вісім різних дискретних вузлів прив'язки. Ділянки мають цілу низку кислотно-лужних властивостей. Метали зв'язуються з цими ділянками, або з однією ділянкою окремо (монодентат), до двох ділянок (бідентат) або, починаючи з моделі VI, до трьох (тридентат). На частці ділянок допускається формування дводентатних комплексів. Починаючи з моделі VI, для кожної бідентатної і тризубчастої групи передбачається присутність трьох підгруп - це ще більше збільшує діапазон міцності зв'язування металів.
Константи зв'язування залежать від іонної сили і електростатичних взаємодій. Умовні константи обчислюються аналогічним чином в моделі V, VI і VII наступним чином:
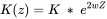
де:
- Z - заряд органічної кислоти (в молі на грам органіки);
- w обчислюється за допомогою:
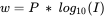
де:
- P - постійний термін (різний для FA і HA, і різний для кожної моделі);
- Це іонна сила.
Тому умовна константа залежить від заряду органічних кислот, а також від іонної сили. Для зв'язування металів розрахунок умовної постійної відбувається аналогічним чином.
Дифузний подвійний шар зазвичай негативно заряджений, тому він зазвичай заселяється катіонами, щоб підтримувати електричну нейтральність. Розрахунки для дифузного подвійного шару однакові для моделі V, моделі VI та моделі VII. Обсяг дифузного подвійного шару розраховується окремо для кожного виду кислоти наступним чином:
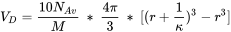
де:
- N Av - число Авогадро;
- М - молекулярна маса кислоти;
- r - радіус молекули (0,8 нм для фульвокислот, 1,72 для гумінових кислот);
- - параметр Дебея-Хюкеля, який залежить від іонної сили.
Просте застосування цієї формули в ситуаціях низької іонної міцності та високого вмісту органічної кислоти призведе до виникнення артефактів (де обсяг дифузного шару може бути розрахований на більше 1 літр/літр). Тому реалізовані деякі «хитрощі», щоб обмежити обсяг дифузного подвійного шару до 25% від загальної кількості.
У разі, якщо кислота має негативний заряд (як це має в більшості випадків), позитивним і нейтральним видам дозволяється входити в дифузний подвійний шар, достатньо, щоб зробити дифузний подвійний шар електрично нейтральним. Коли кислота має позитивний заряд, присутні негативні і нейтральні види.
Концентрація видів у дифузному подвійному шарі розраховується, якщо припустити, що концентрація цього виду в дифузному подвійному шарі залежить від концентрації в об'ємному розчині і шихті.
У формулі:
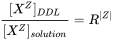
де R обчислюється итеративно, щоб забезпечити дифузний подвійний шар електрично нейтральним.
Додатки
Моделі видоутворення можуть використовуватися для багатьох цілей. В основному можна виділити дві групи додатків. Перша група складається з додатків, призначених для розуміння хімічної поведінки будь-якої системи. Друга група орієнтована на біодоступність.
Хімічна поведінка; лабораторні ситуації
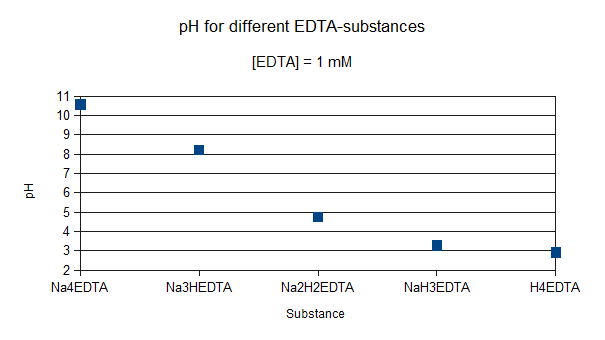
Моделі видоутворення можуть бути корисними для розуміння хімічної поведінки в лабораторних ситуаціях або польових ситуаціях. Наприклад, якщо ви хочете додати ЕДТА до розчину, щоб запобігти випаданню металів, вибір ЕДТА-речовини також визначає рН кінцевого розчину. На малюнку 1 показаний рН 1 мМ розчину ЕДТА для п'яти різних ЕДТА-солей. Це показує, що якщо ви хочете, щоб в кінцевому підсумку з майже нейтральним рішенням, найкращим вибором є додавання ЕДТА як Na 3 Hedta-солі. Додавання іншої солі вимагає додавання або кислоти або основи, або більшої буферної ємності, що, в свою чергу, вплине на хімічну поведінку розчину.
Якщо у вас є польові вимірювання окислювально-відновного потенціалу, моделі видоутворення можуть допомогти передбачити, чи буде залізо присутнім як Fe (II) або Fe (III), що важливо, оскільки Fe (II) поводиться зовсім інакше, ніж Fe (III), а також має зовсім іншу біодоступність. Те ж саме стосується інших елементів, які проходять окислювально-відновні рівноваги, такі як N, S, Cu або Mn.
Фазові реакції можна прогнозувати за допомогою моделей видоутворення, наприклад розчинення карбонату внаслідок реакції газового розчину СО 2. Іншим прикладом є видоутворення в голландській стандартній воді (DSW), часто використовуваному тестовому середовищі для екотоксикологічних експериментів, яке перенасичене по відношенню до CaCo 3 і тому відображає частину Са як осад. Фракція, яка випадає в осад, дуже мала (менше 2% Са), тому на перший погляд здається неважливою, але осад індукує зсув рН 0,22, коефіцієнт майже два в концентрації вільного Н +.
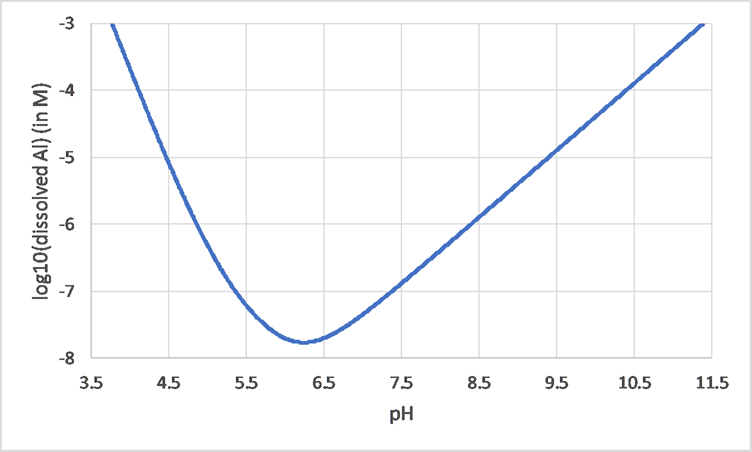
Багато металів є амфотерними і, отже, мають мінімальну розчинність при помірному рН, при цьому розчиняючи більше як при більш високих, так і при нижчих значеннях рН. Це можна легко побачити у випадку Al: на малюнку 2 показана концентрація розчиненого Al як функція рН (зверніть увагу на шкалу журналу для осі Y). Близько рН 6,2, розчинність знаходиться на мінімальному рівні. При більш високих і нижчих значеннях рН розчинність (набагато) вище.
Моделі видоутворення також можуть допомогти зрозуміти відмінності в зростанні організмів або несприятливий вплив на організми, в різних хімічних розчині. Наприклад, на малюнку 3 показано, що зміни видоутворення бору можна очікувати лише між приблизно рН 8 і 10,5, тому, коли ви спостерігаєте біологічну різницю між рН 7 і 8, навряд чи є причиною бору. Мідь з іншого боку (див. Рис. 4) показує відмінності в видоутворенні між рН 7 і 8, тому є більш імовірною причиною різної біологічної поведінки.
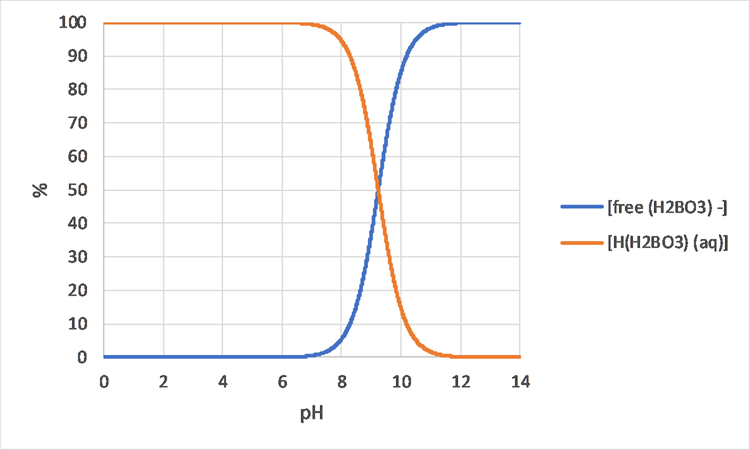
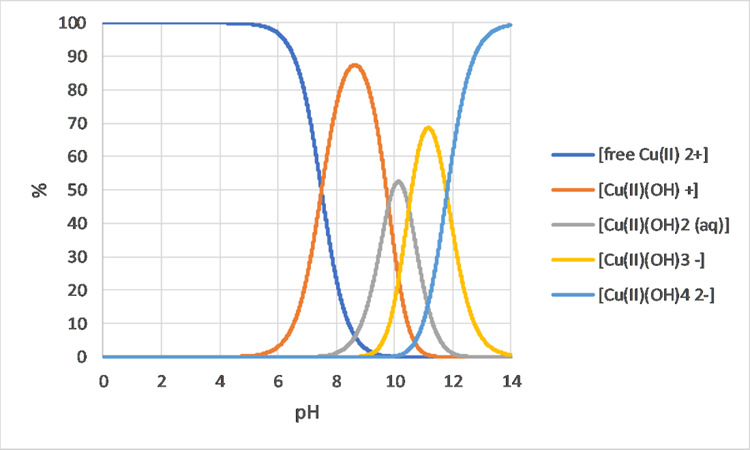
Хімічна поведінка: польові ситуації
У польових ситуаціях хімія зазвичай набагато складніше, ніж в лабораторних умовах. Розпад організмів (включаючи рослини) призводить до величезної різноманітності органічних сполук, таких як фульвокислоти, гумінові кислоти, білки, амінокислоти, вуглеводи тощо Багато з цих сполук сильно взаємодіють з катіонами, деякі також з аніонами або незарядженими молекулами. Крім того, метали легко адсорбуються до глинистих і піщаних частинок, які зустрічаються повсюдно в природі. Щоб зробити його більш складним, суспензія може містити високий вміст органічного матеріалу, який також здатний зв'язувати катіони.
Для комплексоутворення фульвовими та гуміновими кислотами Чайові та колеги розробили об'єднуючу модель (Tipping & Hurley, 1992; Чайові, 1994, 1998; Чайові, Лофти та Сонке, 2011). Найновіша версія, WHAM 7 (Tipping, Lofts & Sonke, 2011), здатна прогнозувати комплексоутворення катіонів фульвокислотами і гуміновими кислотами в широкому діапазоні хімічних обставин, незважаючи на велику різницю в складі цих кислот. Ця модель тепер включена в кілька програм видоутворення.
Суспензія може мати органічний або неорганічний характер. Неорганічна речовина зазвичай складається з (гідр) оксидів металів, таких як Mn, Fe, Al, Si або Ti, і глинистих мінералів. На практиці (гідр) оксиди і глини зустрічаються разом, але взаємні пропорції можуть різко відрізнятися в залежності від джерела. Так як хімічні властивості цих металів (гідр) оксидів глин досить різні, існує величезна різниця в хімічних властивостях неорганічних зважених речовин в різних місцях і різний час. Як наслідок, моделювання взаємодії між розчиненими складовими та зваженими неорганічними речовинами є складним завданням. Тільки вимірюючи деякі властивості зважених неорганічних речовин, моделювання може бути успішно застосовано. Для зважених органічних речовин варіація властивостей також велика, і моделювання є складним завданням.
Біодоступність
Моделі видоутворення корисні для розуміння та оцінки біодоступності металів та інших елементів у тестових середовищах. Тестові середовища часто містять речовини, такі як ЕДТА, щоб тримати метали в розчині. ЕДТА-комплекси взагалі не є біодоступними, тому крім утримання металів у розчині вони також змінюють свою біодоступність. Моделі можуть обчислити видоутворення і допомогти вам оцінити, що насправді відбувається в тестовому середовищі. Часто забутим аспектом є вплив CO 2. СО 2 з атмосфери навколишнього середовища може надходити в розчин або карбонат в розчині (якщо перевищує рівноважну концентрацію) може виходити в атмосферу. Ступінь, до якої відбувається цей обмін, впливає на рН розчину, а також кількість карбонату, який залишається в розчині (карбонати часто погано розчинні).
Аналогічно, в польових ситуаціях моделі можуть допомогти зрозуміти біодоступність елементів. Як зазначалося вище, вплив DOC в даний час можна оцінити належним чином у багатьох ситуаціях, вплив підвішеної речовини залишається складнішим для оцінки. Тим не менш, моделі можуть доставити уявлення за лічені секунди, які в іншому випадку можна отримати лише з великими труднощами.
Моделі
Існує багато програм видоутворення, і кілька з них знаходяться у вільному доступі. Зазвичай вони приймають набір загальних концентрацій в якості вхідних даних, а також інформацію про такі параметри, як рН, окислювально-відновлювально-відновлювальні, концентрація органічного вуглецю і т.д. потім програми обчислюють видоутворення і представляють їх користувачеві. Рівняння не можуть бути розв'язані аналітично, тому потрібна ітераційна процедура. Хоча використовуються різні числові підходи, більшість програм будують набір нелінійних рівнянь балансу маси і вирішують їх простою або вищою математикою. Ускладненням цієї процедури є те, що константи рівноваги залежать від іонної сили розчину, і що цю іонну силу можна обчислити лише тоді, коли відоме видоутворення. Те ж саме стосується осадження твердих тіл. Процедура показана на малюнку 5.
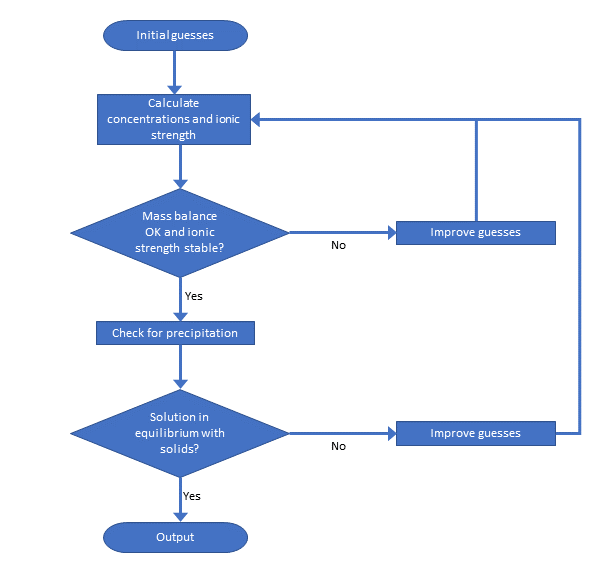
Обмеження
Для моделювання видоутворення необхідні термодинамічні дані для всіх відповідних реакцій рівноваги. Для багатьох рівноваг ця інформація доступна, але не для всіх. Це ускладнює корисність моделювання видоутворення. Крім того, можуть бути великі варіації термодинамічних значень, знайдених в літературі, що призводить до невизначеності щодо правильного значення. Коефіцієнт 10 між найвищим і найнижчим знайденими значеннями не є винятком. Це, звичайно, впливає на надійність розрахунків видоутворення. Для багатьох рівноваг термодинамічні дані доступні лише для стандартної температури 25° C, і немає інформації для оцінки даних при інших температурах, хоча вплив температури може бути досить сильним. Також іонна сила має великий вплив на рівновагу «константи»; існує багато методів, доступних для виправлення впливу іонної сили, але більшість з них в кращому випадку напівемпіричні. Симонін (2017) нещодавно запропонував метод з міцною теоретичною основою; однак дані, необхідні для його методу, доступні лише для кількох комплексів поки що.
Більш принципово, ви повинні розуміти, що програми видоутворення зазвичай обчислюють ситуацію рівноваги, в той час як деякі реакції дуже повільні і, що більш важливо, природа насправді дуже динамічна система і тому ніколи не знаходиться в рівновазі. Якщо система близька до рівноваги, програми видоутворення часто можуть зробити хорошу оцінку фактичної ситуації, але чим динамічніше система, тим більше обережності ви повинні взяти на себе, вважаючи результати програм. Тим не менш, добре усвідомлювати, що хімічна система завжди буде рухатися до ситуації рівноваги, тоді як організми можуть відсунути їх від рівноваги. Фототрофи здатні зрушити систему від її рівноваги ситуації, тоді як декомпозитори та гетеротрофи, як правило, допомагають перемістити систему до її рівноважного стану.
Посилання
Симонін, Ж.-П. Термодинамічна консистенція при моделюванні видоутворення в самокомплексуючих електролітах. Інд. англ. Хім. Рез. 56, 9721-9733.
Чайові, Е., Херлі, М.А. (1992). Уніфікуюча модель катіонного зв'язування гумінових речовин. Геохіміка і Космохіміка Акта 56, 3627 - 3641.
Чайові, Е. WHAM - модель хімічної рівноваги та комп'ютерний код для вод, відкладень та ґрунтів, що включають дискретну сайту/електростатичну модель іонного зв'язування гуміновими речовинами. Комп'ютери та науки про Землю 20, 973 - 1023.
Чайові, Е. Гумінова іонзв'язуюча модель VI: покращений опис взаємодії протонів та іонів металів з гуміновими речовинами. Водна геохімія 4, 3 - 48.
Чайові, Е., Лофтс, С., Сонке, Дж. Гумінова іонзв'язуюча модель VII: переглянута параметризація катион-зв'язування гуміновими речовинами. Хімія навколишнього середовища 8, 228 - 235.
Подальше читання
Штумм, В., Морган, Дж. Дж. (1981). Водна хімія. Джон Вілі та сини, Нью-Йорк.
Море, Ф.М.М., Херінг, Дж. Г. Принципи та застосування водної хімії. Джон Вілі та сини, Нью-Йорк.
Коротко опишемо, що таке моделі видоутворення.
Які фактори визначають видоутворення і як вони можуть бути враховані?
Наведіть два приклади ситуацій, коли моделювання видоутворення може бути корисним.
3.8.4. Моделювання впливу в екологічних масштабах
У підготовці