6.5: Обмеження реагенту та відсотка виходу

Last updated
Save as PDF

Page ID: 21757

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте та визначте теоретичну врожайність, фактичну врожайність та відсоток врожайності.
Визначте обмежуючий реагент з набору реагентів.
Розрахуйте, скільки продукту буде вироблено з граничного реагенту.
Обчисліть, скільки реагенту (ів) залишається, коли реакція завершиться.

врожайність

У всіх попередніх розрахунках, які ми виконували за допомогою збалансованих хімічних рівнянь, ми зробили два припущення:

Реакція йде точно так, як написано.
Реакція протікає повністю.

Насправді відбуваються такі речі, як побічні реакції, які роблять деякі хімічні реакції досить безладними. Наприклад, при фактичному згорянні деяких вуглецевмісних сполук, таких як метан, виробляється деяка кількість СО, а також СО ₂. Однак ми будемо продовжувати ігнорувати побічні реакції, якщо не зазначено інше. Друге припущення, що реакція протікає повністю, більш клопітно. Багато хімічних реакцій не приступають до завершення, як написано, з різних причин. Коли ми розраховуємо кількість продукту, припускаючи, що весь реагент реагує, ми обчислюємо теоретичний вихід - кількість, яка теоретично виробляється, як розрахована за допомогою збалансованої хімічної реакції.

Однак у багатьох випадках це не те, що насправді відбувається. У багатьох випадках під час хімічної реакції виробляється менше - іноді, набагато менше - продукту. Кількість, яка фактично виробляється в реакції, називається фактичним виходом. За визначенням, фактична прибутковість менше або дорівнює теоретичній прибутковості. Якщо його немає, значить, допущена помилка.

І теоретичні врожаї, і фактичні врожаї виражаються в одиницях кротів або грамах. Також часто можна побачити щось, що називається відсотковою прибутковістю. Відсоток прибутковості являє собою порівняння між фактичною прибутковістю і теоретичною прибутковістю і визначається як

\[ \text{percent yield} = \dfrac{\text{actual yield}}{\text{theoretical yield}} \times 100\% \label{yield}\]

Не має значення, чи виражені фактична і теоретична врожайність в кротах або грамах, якщо вони виражені в одних і тих же одиницях. Однак процентна прибутковість завжди має одиниці відсотків. Правильний відсоток врожайності становить від 0% до 100%. У лабораторії студент іноді отримуватиме врожайність, яка, здається, перевищує 100%. Зазвичай це відбувається, коли продукт нечистий або змочений розчинником, таким як вода. Якщо це не так, то учень, мабуть, допустив помилку при зважуванні або реагентів, або продуктів. Закон збереження маси поширюється навіть на бакалаврат хімії лабораторних експериментів. 100% вихід означає, що все працювало ідеально, і хімік отримав весь продукт, який міг бути проведений. Той, хто намагався зробити щось таке просте, як наповнити сільничку або додати масло в двигун автомобіля, не проливаючи, знає невірогідність 100% виходу. З іншого боку, вихід 0% означає, що продукт не був отриманий. Відсоток прибутковості 80% - 90% зазвичай вважається хорошим до відмінним; прибутковість 50% є лише справедливою. Частково через проблеми та витрати на утилізацію відходів промислові виробничі об'єкти стикаються зі значним тиском для оптимізації врожайності продукції та їх максимально наближення до 100%.

Приклад\(\PageIndex{1}\):

Робочий реагує 30,5 г Zn з азотною кислотою і випаровує воду, що залишилася з отриманням 65,2 г Zn (NO ₃) ₂. Що таке теоретична прибутковість, фактична прибутковість і відсоток прибутковості?

\[\ce{Zn(s) + 2HNO_3(aq) → Zn(NO_3)_2(aq) + H_2(g)} \nonumber \]

Рішення

Масово-масовий розрахунок може бути виконаний для визначення теоретичного виходу. Нам потрібні молярні маси Zn (65,39 г/моль) і Zn (NO ₃) ₂ (189,41 г/моль). У три етапи розрахунок маси і маси відбувається:

\[30.5\cancel{g\, Zn}\times \frac{1\, \cancel{mol\, Zn}}{65.39\cancel{g\, Zn}}\times \frac{1\, \cancel{mol\, Zn(NO_{3})_{2}}}{1\cancel{mol\, Zn}}\times \frac{189.41\, g\, Zn(NO_{3})_{2}}{1\cancel{mol\,Zn(NO_{3})_{2}}}=88.3\, g\, Zn(NO_{3})_{2}\nonumber \]

Таким чином, теоретичний вихід становить 88,3 г Zn (NO ₃) ₂. Фактична врожайність - це сума, яка була фактично зроблена, яка склала 65,2 г Zn (NO ₃) ₂. Для обчислення процентної прибутковості беремо фактичну прибутковість і ділимо її на теоретичну дохідність і множимо на 100 (Equation\ ref {yield}):

\[\frac{65.2\, g\, Zn(NO_{3})_{2}}{88.3\, g\,Zn(NO_{3})_{2}}\times 100\%=73.8\%\nonumber \]

Працівник досяг майже трьох чверті можливого врожаю.

Вправа\(\PageIndex{1}\)

Синтез одержав 2,05 г NH ₃ з 16,5 г N ₂. Що таке теоретична прибутковість і процентна прибутковість?

\[N_2(g) + 3H_2(g) → 2NH_3(g)\nonumber \]

*Технічно це оборотна реакція (з подвійними стрілками), але для цієї вправи вважають її незворотною (одинарна стрілка).

Відповідь

теоретичний вихід = 20,1 г; відсоток врожайності = 10,2%

Хімія всюди: фактичні врожаї в синтезі та очищенні наркотиків

Багато препаратів є продуктом декількох етапів хімічного синтезу. Кожен крок зазвичай відбувається з менш ніж 100% прибутковістю, тому загальний відсоток прибутковості може бути дуже малим. Загальне правило полягає в тому, що загальний відсоток виходу є добутком відсотків врожайності окремих етапів синтезу. Для синтезу наркотиків, який має багато кроків, загальний відсоток виходу може бути дуже крихітним, що є одним з факторів величезної вартості деяких препаратів. Наприклад, якщо 10-ступінчастий синтез має відсотковий вихід 90% для кожного кроку, загальний вихід для всього синтезу становить лише 35%. Багато вчених щодня працюють, намагаючись покращити відсоткову врожайність кроків синтезу, щоб зменшити витрати, покращити прибуток та мінімізувати відходи.

Навіть очищення складних молекул в лікарську чистоту підлягають відсоткової врожайності. Розглянемо очищення від нечистого альбутеролу. Альбутерол (C ₁₃ H ₂₁ NO ₂; супутній малюнок) - це інгаляційний препарат, який використовується для лікування астми, бронхіту та інших обструктивних захворювань легень. Він синтезується з норадреналіну, природного гормону і нейромедіатора. Його початковий синтез робить дуже нечистий альбутерол, який очищається в п'ять хімічних етапів. Деталі кроків нас не стосуються; лише відсотки врожайності роблять:

нечистий альбутерол → проміжний А	відсоток прибутковості = 70%
проміжний A → проміжний B	відсоток прибутковості = 100%
проміжний B → проміжний C	відсоток прибутковості = 40%
проміжний С → проміжний D	відсоток прибутковості = 72%
проміжний продукт D → альбутерол очищений	відсоток прибутковості = 35%
загальний відсоток прибутковості = 70% × 100% × 40% × 72% × 35% = 7,5%

Тобто лише близько однієї чотирнадцятої частини вихідного матеріалу було перетворено в очищений препарат. Це демонструє одну з причин, чому деякі препарати настільки дорогі - багато матеріалу втрачається при виготовленні фармацевтичної високої чистоти.

Дитина, яка використовує альбутерол інгалятор, контейнер альбутеролу ліки та молекулярну модель молекули альбутеролу показані на трьох комбінованих зображеннях. — \(\PageIndex{1}\)Малюнок Дитина, яка використовує альбутерол інгалятор, контейнер альбутеролу ліки та молекулярну модель молекули альбутеролу. Джерело: Фото ліворуч © Thinkstock. Фото в центрі люб'язно надано Інтропін, http://commons.wikimedia.org/wiki/Fi...te_%281%29.JPG.

обмежувальний реагент

У всіх розглянутих до цього часу прикладах реагенти передбачалися присутніми в стехіометричних кількостях. Отже, жоден з реагентів не залишився після закінчення реакції. Це часто бажано, як у випадку з космічним човником, де надлишок кисню або водню був не тільки додатковим вантажем для перевезення на орбіту, але і небезпечним для вибуху. Однак частіше реагенти присутні в мольних співвідношеннях, які не збігаються зі співвідношенням коефіцієнтів в збалансованому хімічному рівнянні. Як результат, один або кілька з них не будуть повністю використані, а залишаться після завершення реакції. У цій ситуації кількість продукту, яке можна отримати, обмежується кількістю тільки одного з реагентів. Реагент, який обмежує кількість одержуваного продукту, називається граничним реагентом. Реагент, який залишається після того, як реакція пішла до завершення, знаходиться в надлишку.

Розглянемо нехімічний приклад. Припустимо, ви запросили друзів на вечерю і хочете спекти тістечка на десерт. Ви знайдете дві коробки суміші брауні у своїй коморі і бачите, що кожна упаковка вимагає двох яєць. Таким чином, збалансоване рівняння для приготування брауні

\[ 1 \,\text{box mix} + 2 \,\text{eggs} \rightarrow 1 \, \text{batch brownies} \label{3.7.1}\]

Якщо у вас десяток яєць, який інгредієнт визначить кількість партій тістечок, які ви зможете приготувати? Оскільки кожна коробка суміші брауні вимагає двох яєць, а у вас є дві коробки, вам потрібно чотири яєць. Дванадцять яєць - це на вісім більше яєць, ніж потрібно. Хоча співвідношення яєць до коробок в 2:1, співвідношення у вашому розпорядженні становить 6:1. Отже, яєчка є інгредієнтом (реагентом), присутнім у надлишку, а суміш брауні є обмежуючим реагентом. Навіть якщо у вас був холодильник, повний яєць, ви могли зробити тільки дві партії тістечок.

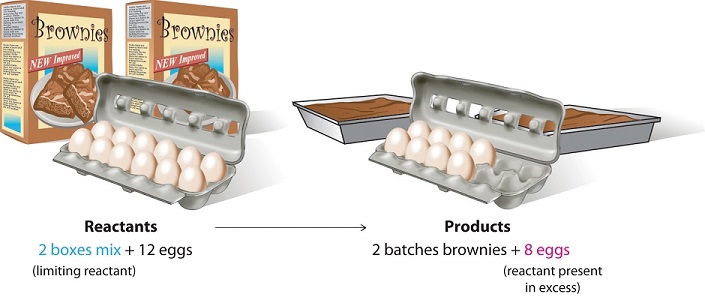
Малюнок \(\PageIndex{1}\): Поняття обмежуючого реагенту при приготуванні тістечок

Подібна ситуація існує для багатьох хімічних реакцій: зазвичай у вас закінчується один реагент, перш ніж всі інші реагенти відреагують. Реагент, з якого ви закінчуєте, називається обмежуючим реагентом; т інші реагенти або реагенти вважаються надлишковими. Найважливішим навиком оцінки умов хімічного процесу є визначення того, який реагент є граничним реагентом, а який в надлишку.

Ключ до визнання того, який реагент є обмежуючим реагентом, базується на розрахунку моль-маси або маси маси: залежно від того, який реагент дає меншу кількість продукту, є граничним реагентом. Що нам потрібно зробити, це визначити кількість одного продукту (або молі, або маси), припускаючи, що всі кожен реагент реагує. Який би реагент не дає найменшу кількість цього конкретного продукту, є граничним реагентом. Не має значення, який продукт ми використовуємо, якщо ми використовуємо один і той же кожен раз. Не має значення, чи ми визначаємо кількість моль або грамів цього продукту; однак незабаром ми побачимо, що знання кінцевої маси продукту може бути корисним.

Наприклад, розглянемо таку реакцію:

\[4As(s) + 3O_2(g) → 2As_2O_3(s)\nonumber \]

Припустимо, ми починаємо реакцію з 50,0 г As і 50,0 г O ₂. Який з них є обмежуючим реагентом? Потрібно виконати два розрахунки моль-маси, кожен з яких припускає, що кожен реагент реагує повністю. Потім порівнюємо кількість виробленого кожним продукту і визначаємо, яке менше.

Розрахунки такі:

\[50.0\cancel{g\, As}\times \frac{1\cancel{mol\, As}}{74.92\cancel{g\, As}}\times \frac{2\, mol\, As_{2}O_{3}}{4\cancel{mol\, As}}=0.334\, mol\, As_{2}O_{3}\nonumber \]

\[50.0\cancel{g\, O_{2}}\times \frac{1\cancel{mol\, O_{2}}}{32.00\cancel{g\, O_{2}}}\times \frac{2\, mol\, As_{2}O_{3}}{3\cancel{mol\, O_{2}}}=1.04\, mol\, As_{2}O_{3}\nonumber \]

Порівнюючи ці дві відповіді, зрозуміло, що 0,334 моль As ₂ O ₃ менше 1,04 моль As ₂ O ₃, тому миш'як є граничним реагентом. Якщо ця реакція буде проведена в цих початкових умовах, миш'як закінчиться до того, як закінчиться кисень. Ми говоримо, що кисень «в надлишку».

Визначення граничного реагенту, значить, нескладне. Однак зазвичай виникають два пов'язаних питання: (1) яка маса продукту (або продуктів) тоді фактично формується? і (2) яка маса якого реагенту залишилася? На перше питання однозначно відповісти: просто виконайте перетворення від кількості молей утворився продукту в його масу, використовуючи його молярну масу. Для As ₂ O ₃ молярна маса становить 197,84 г/моль; знаючи, що ми сформуємо 0,334 моль As ₂ O ₃ за заданих умов, отримаємо

\[0.334\cancel{mol\, As_{2}O_{3}}\times \frac{197.84\, g\, As_{2}}{\cancel{1\, mol\, As_{2}O_{3}}}=66.1\, g\, As_{2}O_{3}\nonumber \]

Друге питання дещо заплутаніше, щоб відповісти. По-перше, ми повинні зробити розрахунок маси маси, що стосується граничного реагенту (тут, As) з іншим реагентом (O ₂). Після того, як ми визначимо масу O ₂, яка відреагувала, ми віднімаємо її з початкової суми, щоб визначити суму, що залишилася. Згідно з розрахунком мас-маса,

\[50.0\cancel{g\, As}\times \frac{1\cancel{mol\, As}}{74.92\cancel{g\, As}}\times \frac{3\cancel{mol\, O_{2}}}{4\cancel{mol\, As}}\times \frac{32.00\, g\, O_{2}}{\cancel{1\, mol\, O_{2}}}=16.0\, g\, O_{2}\; reacted\nonumber \]

Оскільки ми відреагували 16,0 г нашого вихідного O ₂, ми віднімаємо це з початкової кількості, 50,0 г, щоб отримати масу O ₂, що залишилася:

50,0 г О ₂ − 16,0 г О ₂ відреагував = 34,0 г О ₂ залишилося

Ви повинні пам'ятати, щоб виконати це остаточне віднімання, щоб визначити суму, що залишилася; поширеною помилкою є повідомлення про 16,0 г як суму, що залишилася.

Приклад\(\PageIndex{1}\):

Кількість 5,00 г Rb поєднується з 3,44 г MgCl ₂ відповідно до цієї хімічної реакції:

\[2R b(s) + MgCl_2(s) → Mg(s) + 2RbCl(s) \nonumber\nonumber \]

Яка маса Mg утворюється, і яка маса якого реагенту залишилася?

Рішення

Оскільки питання задається питанням, яка маса магнію утворюється, ми можемо виконати два розрахунки мас-маса і визначити, яка кількість менше.

\[5.00\cancel{g\, Rb}\times \frac{1\cancel{mol\, Rb}}{85.47\cancel{g\, Rb}}\times \frac{1\cancel{mol\, Mg}}{2\cancel{mol\, Rb}}\times \frac{24.31\, g\, Mg}{\cancel{1\, mol\, Mg}}=0.711\, g\, Mg \nonumber \]

\[3.44\cancel{g\, MgCl_{2}}\times \frac{1\cancel{mol\, MgCl_{2}}}{95.21\cancel{g\, MgCl_{2}}}\times \frac{1\cancel{mol\, Mg}}{1\cancel{mol\, MgCl_{2}}}\times \frac{24.31\, g\, Mg}{\cancel{1\, mol\, Mg}}=0.878\, g\, Mg \nonumber \]

0,711 г Mg є меншою кількістю, тому асоційований реагент - 5,00 г RB - є граничним реагентом. Щоб визначити, скільки залишилося іншого реагенту, ми повинні зробити ще один розрахунок маси маси, щоб визначити, яка маса MgCl2 вступила в реакцію з 5,00 г Rb, а потім відняти кількість, що відреагувала від початкової кількості.

\[5.00\cancel{g\, Rb}\times \frac{1\cancel{mol\, Rb}}{85.47\cancel{g\, Rb}}\times \frac{1\cancel{mol\, MgCl_{2}}}{2\cancel{mol\, Rb}}\times \frac{95.21\, g\, Mg}{\cancel{1\, mol\, MgCl_{2}}}=2.78\, g\, MgCl_{2}\: \: reacted \nonumber \]

Тому що ми почали з 3,44 г MgCl2, ми маємо

3,44 г MgCl2 − 2,78 г MgCl2 відреагували = 0,66 г MgCl2 ліворуч

Вправа\(\PageIndex{1}\)

З огляду на перераховані початкові кількості, що таке граничний реагент, і яка маса залишкового реагенту?

\[\underbrace{22.7\, g}_{MgO(s)}+\underbrace{17.9\, g}_{H_2S}\rightarrow MgS(s)+H_{2}O(l) \nonumber \]

Відповідь: Н ₂ S є граничним реагентом; 1,5 г MgO залишаються.

Резюме

Теоретичний вихід - це розрахунковий вихід за допомогою збалансованої хімічної реакції. Фактичний вихід - це те, що насправді виходить в хімічній реакції. Відсоток прибутковості - це порівняння фактичної прибутковості з теоретичною прибутковістю.

Граничним реагентом є реагент, який виробляє найменшу кількість продукту. Масово-масові розрахунки дозволяють визначити, скільки виробляється продукту і скільки залишилося інших реагентів.