Skip to main content
LibreTexts - Ukrayinska

14.4: Закон Чарльза

  1. Last updated
  2. Save as PDF
  • Page ID
    19698

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Свіжовипечений хліб виходить легким і пухнастим в результаті дії дріжджів на цукор. Дріжджі перетворюють цукор в вуглекислий газ, який при високих температурах змушує тісто розширюватися. Кінцевий результат - приємне ласощі, особливо при покритті розтопленим вершковим маслом.

    Закон Чарльза

    Французький фізик Жак Шарль (1746-1823) вивчав вплив температури на об'єм газу при постійному тиску. Закон Чарльза стверджує, що обсяг даної маси газу змінюється безпосередньо в залежності від абсолютної температури газу, коли тиск підтримується постійним. Абсолютна температура - це температура, виміряна за шкалою Кельвіна. Шкала Кельвіна повинна використовуватися, оскільки нуль за шкалою Кельвіна відповідає повній зупинці молекулярного руху.

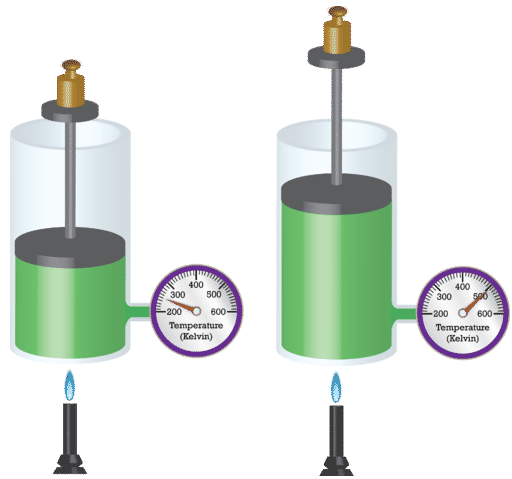
    Малюнок\(\PageIndex{1}\): Коли ємність замкнутого газу нагрівається, його молекули збільшуються кінетична енергія і виштовхують рухливий поршень назовні, в результаті чого збільшується об'єм. (КУБ.СМ ПО-НК; К-12)

    Математично прямий зв'язок Закону Карла можна представити наступним рівнянням:

    \[\frac{V}{T} = k\nonumber \]

    Як і у випадку з законом Бойла,\(k\) є постійним тільки для даного зразка газу. У таблиці нижче наведені дані про температуру і обсяг для заданої кількості газу при постійному тиску. Третій стовпець є постійною для цього конкретного набору даних і завжди дорівнює обсягу, поділеному на температуру Кельвіна.

    Температура\(\left( \text{K} \right)\) Обсяг\(\left( \text{mL} \right)\) \(\frac{V}{T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\)
    Таблиця\(\PageIndex{1}\): Дані про температуру та обсяг
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">50 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">20 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 100 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">40 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 150 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">60 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 200 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">80 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">300 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 120 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 500 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 200 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40
    \ (\ left (\ text {K}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; "> 1000 \ (\ left (\ text {mL}\ праворуч)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр; ">400 \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;" >0.40

    Коли ці дані позначені графіком, результатом є пряма лінія, що свідчить про пряму залежність, показану на малюнку нижче.

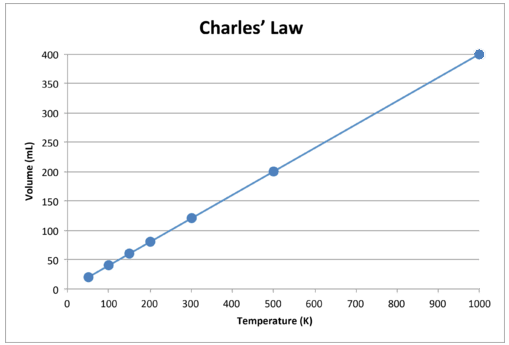
    Малюнок\(\PageIndex{2}\): Обсяг газу збільшується зі збільшенням температури Кельвіна.

    Зверніть увагу, що лінія йде точно до початку, а це означає, що в міру наближення абсолютної температури газу до нуля її обсяг наближається до нуля. Однак, коли газ доводиться до надзвичайно холодних температур, його молекули зрештою конденсуються в рідкому стані до досягнення абсолютного нуля. Температура, при якій відбувається ця зміна в рідкий стан, змінюється для різних газів.

    Закон Чарльза також може бути використаний для порівняння мінливих умов для газу. Тепер використовуємо\(V_1\) і\(T_1\) відстоювати початковий об'єм і температуру газу, поки\(V_2\) і\(T_2\) витримуємо кінцевий обсяг і температуру. Математичним співвідношенням Закону Чарльза стає:

    \[\frac{V_1}{T_1} = \frac{V_2}{T_2}\nonumber \]

    Це рівняння може бути використано для обчислення будь-якої з чотирьох величин, якщо відомі інші три. Пряма залежність буде триматися тільки в тому випадку, якщо температури виражені в Кельвіні. Температури в Цельсієм не працюватимуть. Згадайте відносини, які\(\text{K} = \: ^\text{o} \text{C} + 273\).

    Приклад\(\PageIndex{1}\)

    Повітряна куля наповнюється до обсягу при\(2.20 \: \text{L}\) температурі\(22^\text{o} \text{C}\). Потім балон нагрівають до температури\(71^\text{o} \text{C}\). Знайдіть новий обсяг повітряної кулі.

    Крок 1: Перерахуйте відомі величини та плануйте проблему.
    Відомий
    • \(V_1 = 2.20 \: \text{L}\)
    • \(T_1 = 22^\text{o} \text{C} = 295 \: \text{K}\)
    • \(T_2 = 71^\text{o} \text{C} = 344 \: \text{K}\)
    Невідомий

    Використовуйте закон Чарльза, щоб вирішити для невідомого тому\(\left( V_2 \right)\). Температури вперше були перетворені на Кельвіна.

    Крок 2: Вирішіть.

    По-перше, переставити рівняння алгебраїчно, щоб вирішити для\(V_2\).

    \[V_2 = \frac{V_1 \times T_2}{T_1}\nonumber \]

    Тепер підставляємо відомі величини в рівняння і вирішуємо.

    \[V_2 = \frac{2.20 \: \text{L} \times 344 \: \text{K}}{295 \: \text{K}} = 2.57 \: \text{L}\nonumber \]

    Крок 3: Подумайте про свій результат.

    Обсяг збільшується з підвищенням температури. Результат має три значущі цифри.

    Резюме