2.3: Бінарна рідина

Ентропія змішування

Термодинаміка процесу змішування важлива для фазових рівноваг, гідрофобності, розчинності та пов'язаних з ними проблем розв'язання. Процес змішування двох чистих речовин\(A\) і\(B\) показаний нижче. Визначаємо склад системи через кількість\(A\) і\(B\) частинок:\(N_A\)\(N_B\) і загальне число частинок\(N = N_A + N_B\), яке також дорівнює числу осередків. Починаємо з двох ємностей однорідних чистих рідин і змішуємо їх разом, зберігаючи загальну кількість клітин постійною. У випадку з чистими рідинами перед змішуванням спочатку заповнюються всі осередки ємності, тому є тільки один доступний мікростан\(\Omega_{\text{pure}} = 1\), і

\[S_{\text{pure}} = k_B \ln 1 = 0\nonumber\]

При змішуванні двох ємностей кількість можливих мікростанів задається біноміальним розподілом:\(\Omega_{\text{mix}} = N!/N_A! N_B!\).

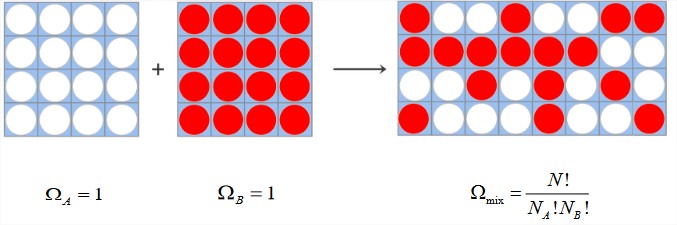
Якщо ці частинки не мають взаємодій, кожен мікростан однаково вірогідний, і подібно до екв. (2.2.2) ми отримуємо ентропію суміші як

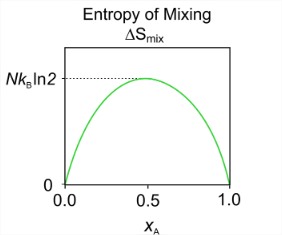
\[S_{\text{mix}}=-N k_{B}\left(x_{A} \ln x_{A}+x_{B} \ln x_{B}\right) \label{eq2.3.1}\]

Для суміші визначаємо мольні фракції для двох компонентів:\(x_A = N_A / N\) і\(x_B = N_B / N\). Як і раніше, з\(x_A\) і\(x_B < 1\), ентропія для суміші завжди позитивна. Ентропія змішування потім розраховується з\(\Delta S_{\text{mix}} = S_{\text{mix}} - (S_{\text{pure A}} + S_{\text{pure B}})\). Так як ентропія чистих речовин в цій моделі дорівнює нулю,\(\Delta S_{\text{mix}} = S_{\text{mix}}\). Ділянка цієї функції як функції мольних фракцій ілюструє, що максимальна ентропія має суміш\(x_A = x_B = 0.5\).

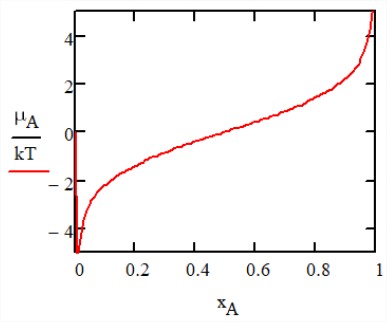
При відсутності взаємодій між частинками вільна енергія змішування чисто ентропна с\(\Delta F_{\text{mix}} = -T \Delta S_{\text{mix}}\). Хімічний потенціал\(A\) частинок\(\mu_A\) описує вільну енергію, необхідну для заміни частинки\(B\) додатковою\(A\) частинкою, і виходить з

\[\begin{array} {l} {\mu_i = \left (\dfrac{\partial F}{\partial N_i} \right )_{T, V, \{N_{j \ne i}\}}} \\ {\mu_A = -k_B T (\ln x_A - \ln x_B) = -\mu B} \end{array} \nonumber\]

Ця крива ілюструє зростаючу проблему пошуку доступного простору у міру збільшення фракції упаковки.

Міжмолекулярна взаємодія

Щоб подивитися на реальні системи, ми додаємо взаємодію між частинками, призначивши енергію взаємодії\(\omega\) між двома клітинами, які знаходяться в контакті. Енергія взаємодії може бути позитивною (дестабілізуючою) або негативною (сприятливою).

При додаванні міжмолекулярних взаємодій кожен мікростан матиме виразну енергію, канонічну функцію поділу можна отримати з еквалайзера. (2.1.1), і інші термодинамічні властивості слідують.

У випадку з сумішшю ми призначаємо окремі енергії взаємодії для кожного\(A-A\) прилеглого\(B-B\), або\(A-B\) пари в заданому мікростані:\(\omega_{AA}, \omega_{BB}, \omega_{AB}\). Як обчислити енергію мікростану? m - загальна кількість молекулярних контактів в обсязі, і їх можна розділити на\(A-A\)\(B-B\), або\(A-B\) контакти:

\[m = m_{AA} + m_{BB} + m_{AB} \nonumber\]

Хоча\(m\) постійний, кількість конкретних контактів\(m_{ij}\) варіюється в залежності від мікростану. Тоді енергію суміші для єдиного\(i^{th}\) мікростану можна записати як

\[E_{\text {mix}}=m_{A A} \omega_{A A}+m_{B B} \omega_{B B}+m_{A B} \omega_{A B} \label{eq2.3.2}\]

а внутрішня енергія походить від ансамблю в середньому з цієї величини. Точний розрахунок внутрішньої енергії від функції розділення вимагатиме суми над усіма можливими конфігураціями з їх індивідуальними контактними номерами. Натомість ми можемо використовувати простіший, приблизний підхід, який використовує стратегію, яка починається з вираження кожного терміна в еквалайзері. (\(\ref{eq2.3.2}\)) з точки зору\(m_{AB}\). Ми знаємо:

\[\begin{array} {rcl} {m_{AA}} & = & {\text{(Total contacts for A) - (Contacts of A with B)}} \\ {} & = & {\dfrac{zN_A}{2} - \dfrac{m_{AB}}{2}} \end{array}\]

\[m_{B B}=\dfrac{z N_{B}}{2}-\dfrac{m_{A B}}{2}\]

Тоді у нас є

\[\begin{array} {rcl} {E_{\text{mix}}} & = & {\left (\dfrac{z\omega_{AA} N_A}{2} \right ) + \left (\dfrac{z\omega_{BB} N_B}{2} \right ) + m_{AB} \left (\omega_{AB} - \dfrac{\omega_{AA} + \omega_{BB}}{2} \right )} \\ {} & = & {U_{\text{pure A}} + U_{\text{pure B}} + m_{AB} \Delta \omega} \end{array} \label{eq2.3.5}\]

Останній термін в цьому виразі - це половина зміни енергії взаємодії для перемикання\(A-A\) і\(B-B\) контакту для утворення двох\(A-B\) контактів:

\[\Delta \omega = \left (\omega_{A B} - \dfrac{\omega_{A A} + \omega_{B B}}{2} \right)\]

Ми також визнаємо, що перші два терміни - це лише енергія двох чистих рідин перед змішуванням. Вони обчислюються, взявши кількість осередків в чистій рідині (\(N_i\)) на кількість контактів на клітинку (\(z\)), а потім ділимо на два, щоб не подвоїти підрахунок контактів.

\[U_{\text{pure, i}} = \dfrac{z \omega_{ii} N_{i}}{2}\]

З цими виразами, ур. (\(\ref{eq2.3.5}\)) стає

\[E_{\text{mix}} = U_{\text{pure A}} + U_{\text{pure B}} + m_{AB} \Delta \omega \nonumber\]

Це рівняння описує енергію мікростану в перерахунку на кількість присутніх\(A-B\) контактів\(m_{AB}\).

На даний момент це не особливо корисно, оскільки не практично перераховувати всі можливі мікростани та їх відповідні\(m_{AB}\). Щоб спростити наш розрахунок\(U_{\text{mix}}\), ми робимо «наближення середнього поля», яке замінює\(m_{AB}\) його середнім статистичним\(\langle m_{AB} \rangle\):

\[\begin{array} {rcl} {\langle m_{AB} \rangle} & = & {\text{(# of contact sites for A)} \times \text{(probability of contact site being B)}} \\ {} & = & {(N_A z) \left (\dfrac{N_B}{N}\right ) = zx_A x_B N} \end{array}\]

Тоді за енергію для змішаного стану\(U_{\text{mix}} = \langle E_{\text{mix}} \rangle\) отримуємо:

\[U_{\text{mix}} = U_{\text{pure A}} + U_{\text{pure B}} + x_A x_B Nk_B T \chi_{AB}\]

Тут ми ввели параметр безодиничного обміну,

\[\chi_{A B}=\dfrac{z}{k_{B} T} \left (\omega_{A B} - \dfrac{\omega_{A A}+\omega_{B B}}{2} \right ) = \dfrac{z \Delta \omega}{k_{B} T} \label{eq2.3.10}\]

який виражає\(\Delta \omega\) (зміна енергії при перемиканні одного\(A\) і\(B\) з чистого стану в іншу рідину) в одиницях\(k_B T\). Ділення на\(z\) дає середню енергію взаємодії на контакт.

\[\begin{array} {l} {\chi_{AB} > 0 \to \text{unfavorable A-B interaction}} \\ {\chi_{AB} < 0 \to \text{favorable A-B interaction}} \end{array} \nonumber\]

Тепер ми можемо визначити зміну внутрішньої енергії при змішуванні:

\[\begin{array} {rcl} {\Delta U_{\text{mix}} } & = & {(U_{\text{mix}} - U_{\text{pure A}} - U_{\text{pure B}})} \\ {} & = & {x_A x_B N k_B T \chi_{AB}} \end{array} \label{eq2.3.11}\]

Примітка\(\Delta U_{mix}\) як функція складу має своє мінімальне значення для суміші з\(x_A = 0.5\), коли\(\chi_{AB} < 0\).

Зауважте, що в наближенні середнього поля функція канонічного розділу дорівнює

\[Q = \dfrac{N!}{N_A! N_B!} q_A^{N_A} q_B^{N_B} \exp [-U_{\text{mix}}/k_B T]\nonumber\]

Ми зберегли функції внутрішнього молекулярного розділення тут для повноти, але для простих частинок у цій моделі\(q_A = q_B = 1\).

Змішування вільної енергії ¹

Використання eqs. (\(\ref{eq2.3.1}\)) і (\(\ref{eq2.3.11}\)), тепер ми можемо отримати вільну енергію змішування

\[\begin{array} {rcl} {\Delta F_{\text{mix}} } & = & {\Delta U_{\text{mix}} - T \Delta S_{\text{mix}} } \\ {} & = & {Nk_B T (x_A x_B \chi_{AB} + x_A \ln x_A + x_B \ln x_B)} \end{array}\nonumber\]

Ця функція побудована нижче як функція мольного дробу для різних значень обмінного параметра. Коли немає міжмолекулярних взаємодій (\(\chi_{AB} = 0\)), змішування є спонтанним для будь-якої мольної фракції і чисто ентропним. Будь-яка сильно сприятлива\(A-B\) взаємодія (\(\chi_{AB} < 0\)) служить лише для подальшого зменшення вільної енергії для всіх мольних фракцій.

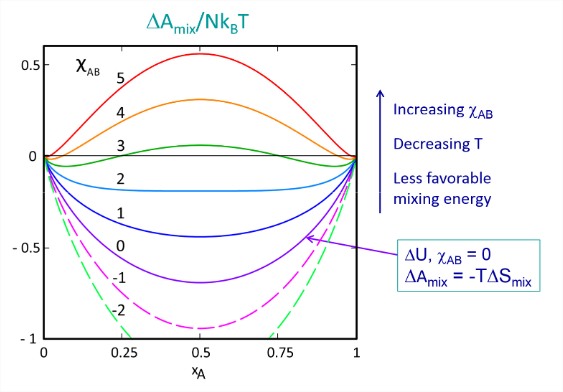
Зі\(\chi_{AB}\) збільшенням ми бачимо, що вільна енергія для змішування зростає, з найбільшими змінами для суміші 50/50. Щоб описати наслідки, давайте розглянемо криву для того\(\chi_{AB} = 3\), для чого певні склади змішуються,\((\Delta F_{\text{mix}} < 0)\) а інші незмішуються\((\Delta F_{\text{mix}} > 0)\).

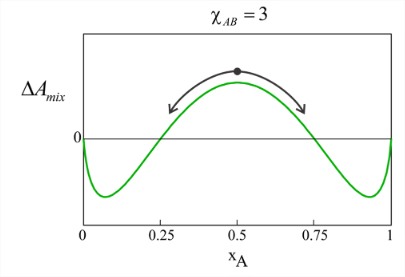
Розглянемо, що буде, якщо приготувати суміш 50/50 цього розчину. Вільна енергія перемішування позитивна при рівноважному складі\(x_A= 0.5\) однорідної суміші, що вказує на те, що два компоненти незмішуються. Однак є й інші склади суміші, які дійсно мають негативну вільну енергію змішування. У цих умовах розчин може розділятися на дві фази таким чином, що\((\Delta F_{\text{mix}}\) зводиться до мінімуму. Це відбувається при мольних частках\(x_A\) = 0,07 & 0,93, що показує нам, що одна фаза буде характеризуватися,\(x_A \gg x_B\) а інша с\(x_A \ll x_B\). Якщо ми приготуємо нерівну суміш з позитивом\((\Delta A_{\text{mix}}\), наприклад\(x_A = 0.3\), система все одно буде мимовільно розділяти фазу, хоча збереження маси буде диктувати, що загальна маса фракції з\(x_A = 0.07\) буде більше маси фракції при\(x_A = 0.93\). Зі\(\chi_{AB}\) збільшенням понад 3, мольна частка меншого компонента зменшується, як очікується, для гідрофобного ефекту. Розглянемо, якщо\(A\) = вода і\(B\) = масло. \(\omega_{BB}\)і\(\omega_{AB}\) бувають дрібними і негативними,\(\omega_{AA}\) бувають великими і негативними, і\(\chi_{AB} \gg 1\).

Критична поведінка

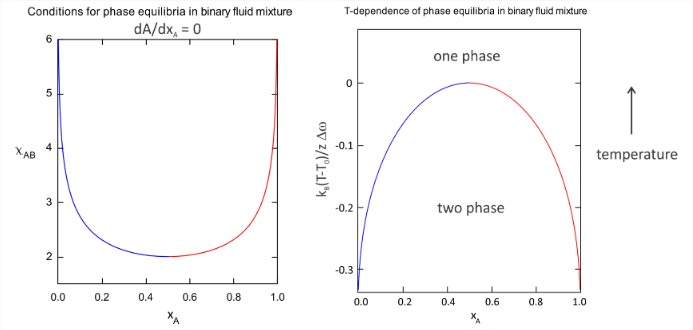
Зверніть увагу, що суміші 50/50 з\(2 < \chi_{AB} < 2.8\) мають негативну вільну енергію змішування для створення єдиної однорідної фази, але система все ще може знижувати вільну енергію далі шляхом фазового поділу. Як видно на малюнку,\(\chi_{AB} = 2\) позначає перехід від однофазних сумішей до двох фазових сумішей, що є підписом критичної точки. Ми можемо знайти умови для фазових рівноваг, розташувавши мінімуми вільної енергії як функцію\(\chi_{AB}\), що призводить до фазових діаграм як функції, так\(\chi_{AB}\) і\(T\) нижче. Критична температура для кросовера від одного до двофазного поведінки є\(T_0\), і\(\Delta \omega\) є середньою диференційованою зміною енергії взаємодії, визначеної в еквалайзері. (\(\ref{eq2.3.10}\)).

Читання

1. К.Ділл і С.Бромберг, Молекулярні рушійні сили: Статистична термодинаміка в біології, хімії, фізиці та нанонауці. (Тейлор і Френсіс Груп, Нью-Йорк, 2010).
2. Гресслі, Полімерні рідини та мережі: структура та властивості. (Гарленд Наука, Нью-Йорк, 2004), Гл. 3.

_____________________________________

1. Дж. Хільдебранд та Р.Л. Скотт, Регулярні рішення. (Прентіс-Холл, Енглвудські скелі, Нью-Джерсі, 1962).