10.3: Видалення фону

Last updated
Save as PDF

Page ID: 17998

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Ще одна форма шуму - систематичний фоновий сигнал, на який накладається цікавить аналітичний сигнал. Наприклад, на наступному малюнку показаний гаусовий сигнал з максимальним значенням 50 по центру при\(x = 125\) накладеному на експоненціальному тлі. Пунктирна лінія - це сигнал Гаусса, який має максимальне значення 50 в\(x = 125\), а суцільна лінія - сигнал, як виміряний, який має максимальне значення 57 ат\(x = 125\).

Малюнок\(\PageIndex{1}\): Гауссовий сигнал (пунктирна лінія) накладається на експоненціальний фон, що дає початок вимірюваному сигналу (суцільна лінія).

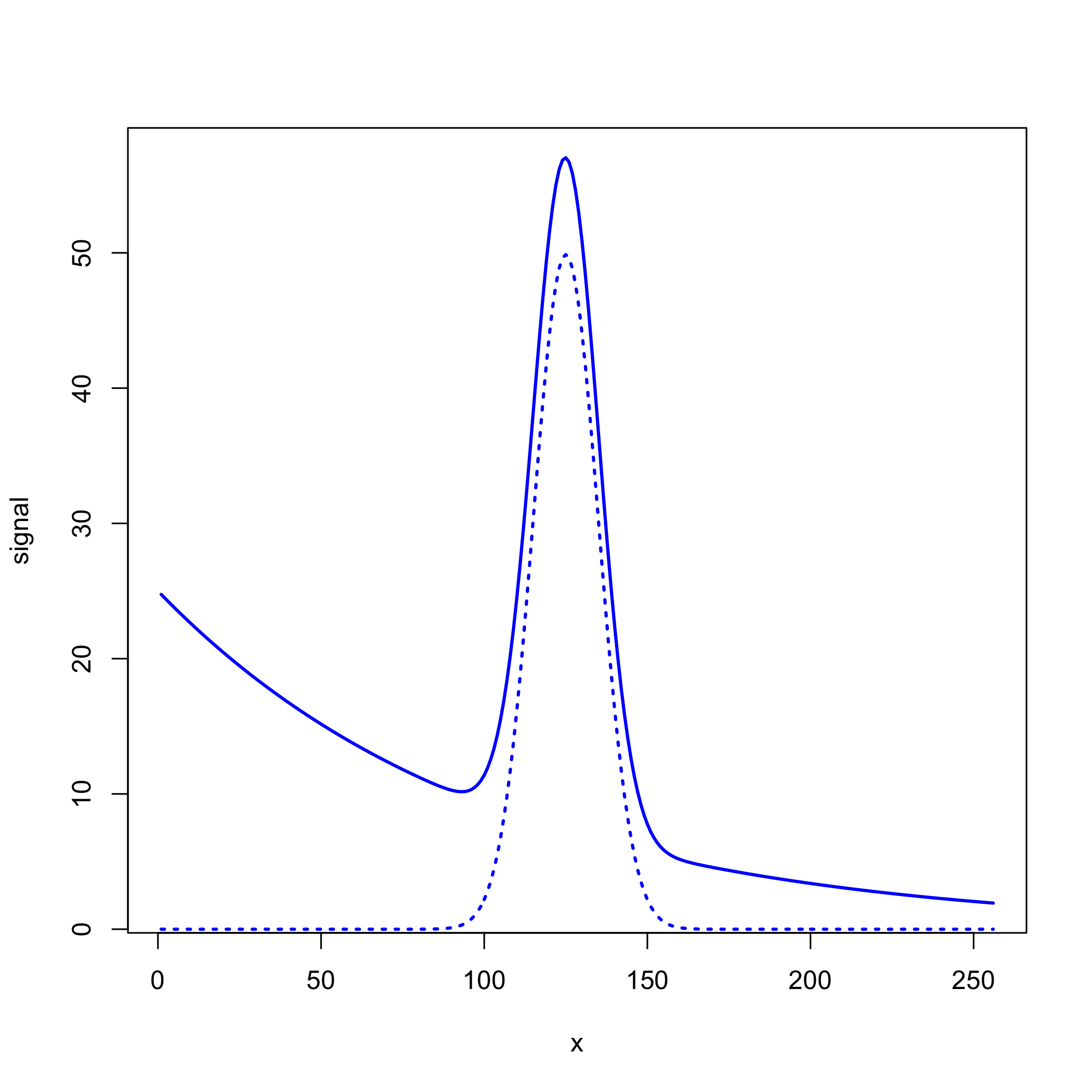
Якщо фоновий сигнал узгоджений у всіх зразках, то ми можемо проаналізувати дані без попереднього видалення його внеску. Наприклад, на наступному малюнку показаний набір калібрувальних стандартів і їх результуюча калібрувальна крива, для якої y -перехоплення 7 дає зміщення, введене фоном.

Малюнок\(\PageIndex{2}\): Коли фон однаковий для всіх калібрувальних стандартів і зразків, то ми можемо побудувати калібрувальну криву без урахування наявності фону.

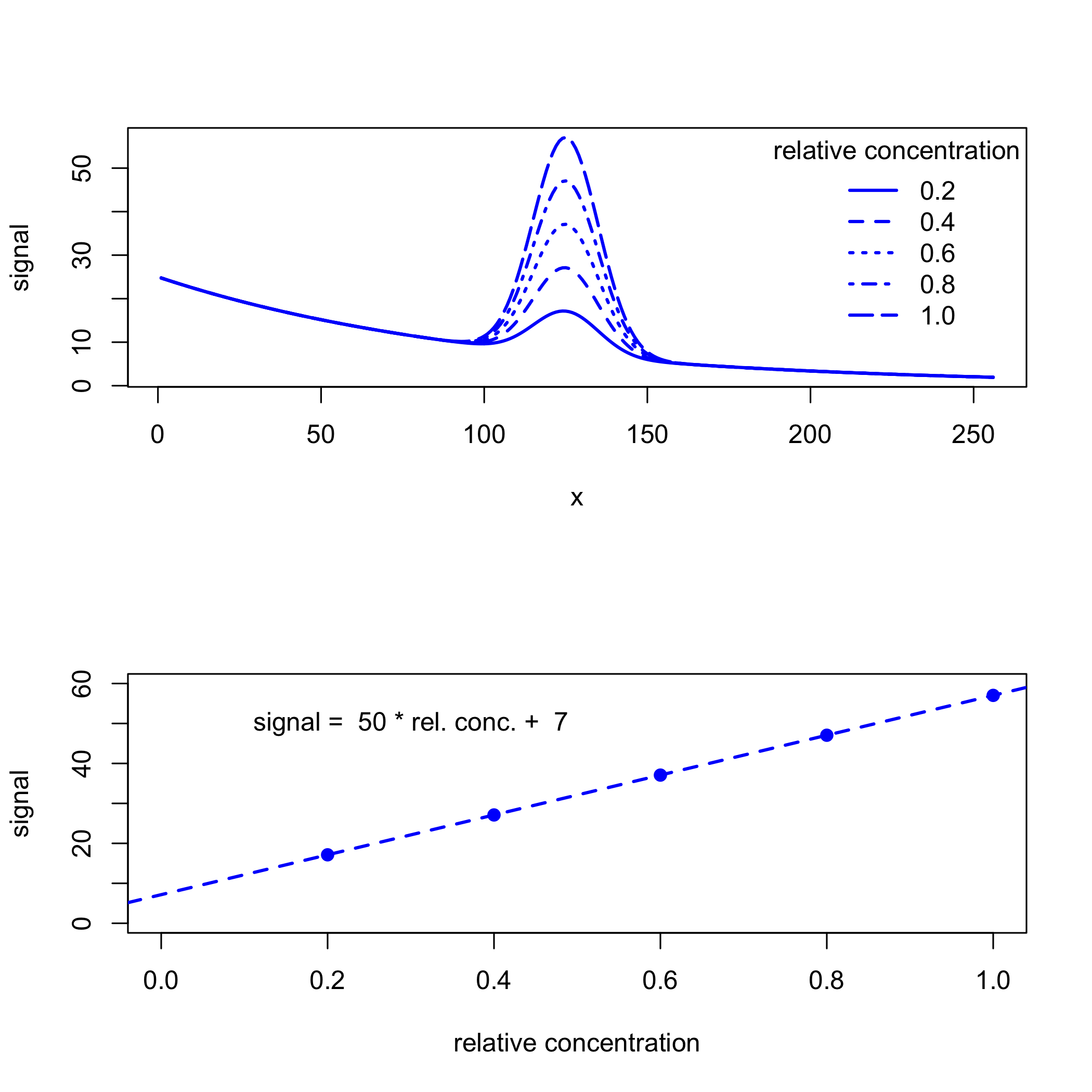
Але фонові сигнали часто не узгоджуються між зразками, особливо коли джерелом фону є властивість зразків, які ми збираємо (наприклад, зразки природної води можуть мати зміни кольору через різницю в концентрації розчиненої органічної речовини) або властивість інструмент, який ми використовуємо (наприклад, зміна інтенсивності джерела з часом). Якщо це правда, наші дані можуть виглядати більше як те, що ми бачимо на наступному малюнку, що призводить до калібрувальної кривої з більшою невизначеністю.

Малюнок\(\PageIndex{3}\): Коли фон не однаковий для всіх стандартів калібрування, якість калібрувальних кривих страждає, що робить його менш корисним для аналізу зразків.

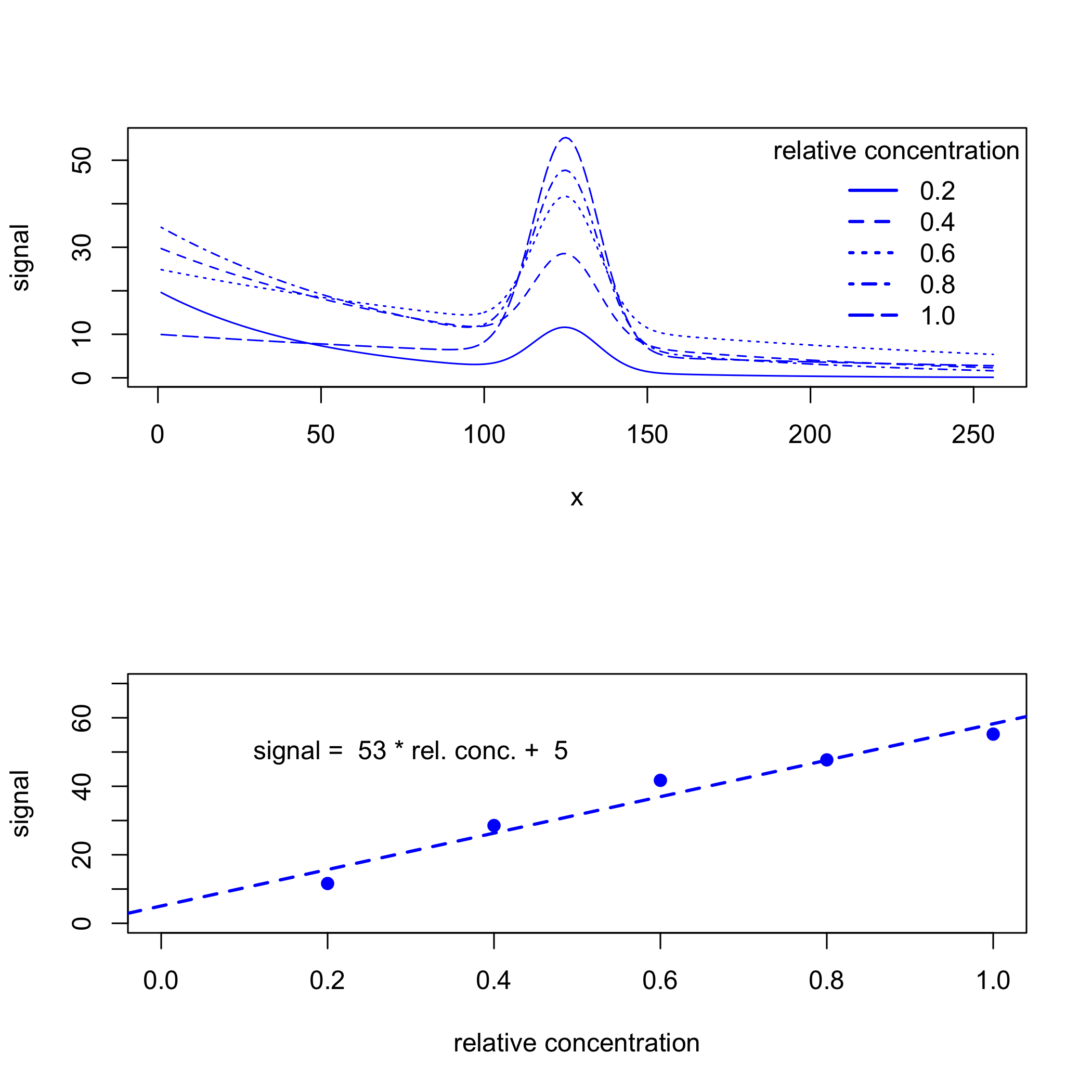
Оскільки фон поступово змінюється зі значеннями для x, тоді як сигнал аналіта швидко змінюється, ми можемо використовувати похідну для розрізнення двох. Один з підходів полягає у використанні фільтра похідних Савіцкі-Голая, використовуючи той самий підхід, описаний в останньому розділі. Наприклад, застосування 7-точкового першого похідного фільтра Савіцкого-Голая з вагами

\[ -3/28 \quad \quad -2/28 \quad \quad -1/28 \quad \quad 0/28 \quad \quad 1/28 \quad \quad 2/28 \quad \quad 3/28 \nonumber\]

до даних на малюнку наводяться результати,\(\PageIndex{3}\) наведені нижче. Калібрувальний сигнал в даному випадку - це різниця між максимальним сигналом і мінімальним сигналом, які показані пунктирними червоними лініями у верхній частині малюнка. Пристосування калібрувальної кривої до даних та y -перехоплення нульової кривої калібрувальної кривої показує, що ми успішно компенсували фонові сигнали.

Рисунок\(\PageIndex{4}\): Застосування фільтра похідних Савицького-Голая до даних калібрувальної кривої на малюнку\(\PageIndex{3}\) виправляє відмінності фонових сигналів, отримуючи покращену калібрувальну криву.

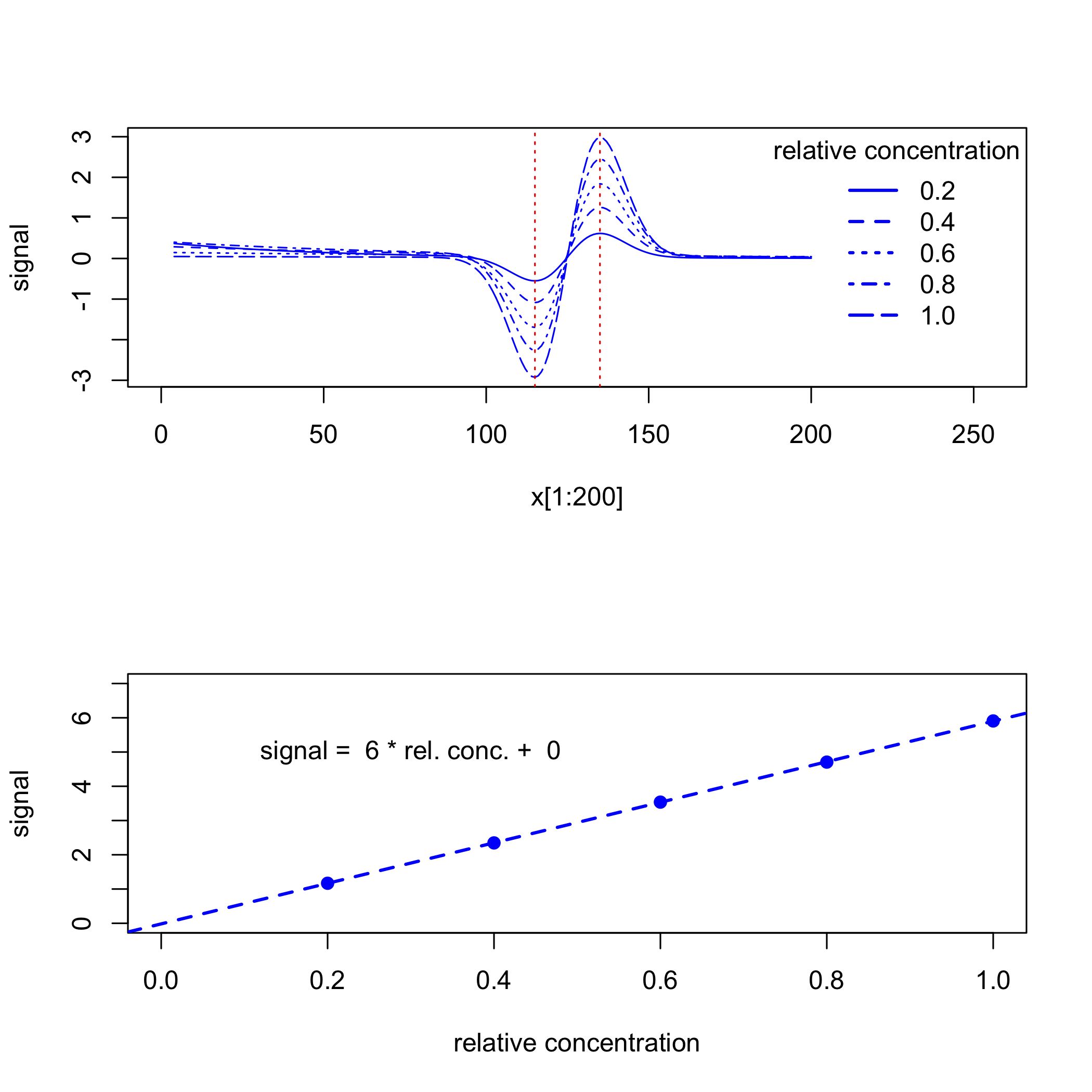
Інші похідні фільтри Савицького-Голая, включаючи фільтри другої похідної, див. Savitzky, A.; Golay, M.J. Anal Chem, 1964, 36, 1627-1639.