13.2: Хімічна кінетика

Найбільш ранні аналітичні методи, засновані на хімічній кінетиці, які вперше з'явилися наприкінці ХІХ ст., скористалися каталітичною активністю ферментів. У типовому методі тієї епохи до розчину додавали фермент, який містив відповідний субстрат, і їх реакція контролювалася протягом фіксованого часу. Активність ферменту визначалася зміною концентрації субстрату. Ферменти також використовувалися для кількісного аналізу перекису водню і вуглеводів. Розвиток хімічних кінетичних методів тривало в першій половині ХХ століття з введенням неферментативних каталізаторів і некаталітичних реакцій.

Незважаючи на різноманітність хімічних кінетичних методів, до 1960 року вони вже не були загального користування. Основним обмеженням для їх більш широкого прийняття була сприйнятливість до значних помилок від неконтрольованих або погано контрольованих змінних - температура і рН є двома такими прикладами - і наявність перешкод, які активують або інгібують каталітичні реакції. До 1980-х років вдосконалення приладобудування та методів аналізу даних компенсували ці обмеження, забезпечивши подальший розвиток хіміко-кінетичних методів аналізу [Pardue, H.L. Чим. Акт 1989, 2016, 69—107].

Теорія і практика

Кожна хімічна реакція відбувається з кінцевою швидкістю, що робить її потенційним кандидатом для хімічного кінетичного методу аналізу. Однак, щоб бути ефективною, хімічна реакція повинна відповідати трьом необхідним умовам: (1) реакція не повинна відбуватися занадто швидко або занадто повільно; (2) ми повинні знати закон швидкості реакції; і (3) ми повинні мати можливість контролювати зміну концентрації принаймні для одного виду. Давайте докладніше розглянемо кожне з цих вимог.

Матеріал в цьому розділі передбачає деяке знайомство з хімічною кінетикою, яка входить до складу більшості курсів загальної хімії. Огляд швидкості реакції, законів швидкості та інтегрованих законів швидкості див. Матеріал у Додатку 17.

Швидкість реакції

Швидкість хімічної реакції - як швидко змінюються концентрації реагентів та продуктів під час реакції - повинна бути досить швидкою, щоб ми могли завершити аналіз за розумний час, але також досить повільною, щоб реакція не досягала рівноваги, поки реагенти змішування. Як практична межа, непросто вивчити реакцію, яка досягає рівноваги протягом декількох секунд без допомоги спеціального обладнання для швидкого перемішування реагентів.

Два приклади приладобудування для вивчення реакцій з швидкою кінетикою ми розглянемо далі в цьому розділі.

Закон про ставку

Друга вимога полягає в тому, що ми повинні знати закон швидкості реакції - математичне рівняння, яке описує, як концентрації реагентів впливають на швидкість - за період, в якому ми проводимо вимірювання. Наприклад, закон швидкості для реакції, яка є першим порядком в концентрації аналіту, А, дорівнює

\[\text { rate }=-\frac{d[A]}{d t}=k[A] \label{13.1}\]

де k - константа швидкості реакції.

Оскільки концентрація А зменшується під час реакцій, d [A] є негативним. Знак мінус у Equation\ ref {13.1} робить швидкість позитивною. Якщо ми вирішимо слідувати продукту, P, то d [P] є позитивним, оскільки концентрація продукту збільшується протягом всієї реакції. В цьому випадку опускаємо знак мінус.

Інтегрований закон ставки часто є більш корисною формою закону ставки, оскільки він є функцією початкової концентрації аналіта. Наприклад, інтегрований закон швидкості для рівняння\ ref {13.1} дорівнює

\[\ln{[A]_t} = \ln{[A]_0} - kt \label{13.2}\]

або

\[[A]_{t}=[A]_{0} e^{-k t} \label{13.3}\]

де [A] ₀ - початкова концентрація аналіта, а [A] _t - концентрація аналіта під час t.

На жаль, більшість реакцій аналітичного інтересу не слідують простому нормовому закону. Розглянемо, наприклад, наступну реакцію між аналітом, А і реагентом, R, для утворення єдиного продукту, P

\[A + R \rightleftharpoons P \nonumber\]

де k _f - постійна швидкості для прямої реакції, а k _r - постійна швидкості для зворотної реакції. Якщо пряма і зворотна реакції відбуваються як поодинокі кроки, то закон ставки дорівнює

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A][R]-k_{r}[P] \label{13.4}\]

Перший член, k _f [A] [R] припадає на втрату А, оскільки він реагує з R, щоб зробити P, а другий член, k _r [P] припадає на формування A як P перетворює назад в A і в R.

Хоча ми знаємо закон швидкості реакції, не існує простої інтегрованої форми, яку ми можемо використовувати для визначення початкової концентрації аналіту. Ми можемо спростити Equation\ ref {13.4}, обмеживши наші вимірювання початком реакції, коли концентрація продукту незначна.

За цих умов ми можемо ігнорувати другий член в Equation\ ref {13.4}, що спрощує

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A][R] \label{13.5}\]

Інтегрований закон швидкості для Equation\ ref {13.5}, однак, все ще занадто складний, щоб бути аналітично корисним. Ми можемо ще більше спростити кінетику шляхом внесення подальших коригувань в умови реакції [Mottola, H.A. Anal. Чим. Акта 1993, 280, 279—287]. Наприклад, ми можемо забезпечити псевдо-кінетику першого порядку, використовуючи великий надлишок R так, щоб його концентрація залишалася по суті постійною протягом часу, коли ми контролюємо реакцію. За цих умов Equation\ ref {13.5} спрощує

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A][R]_{0}=k^{\prime}[A] \label{13.6}\]

де k ′ = к _ф [R] ₀. Інтегрований закон швидкості для рівняння\ ref {13.6} тоді дорівнює

\[\ln{[A]_t} = \ln{[A]_0} - k’t \label{13.7}\]

або

\[[A]_{t}=[A]_{0} e^{-k^{\prime} t} \label{13.8}\]

Можливо, навіть можна налаштувати умови так, щоб ми використовували реакцію в умовах псевдонульового порядку.

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A]_{0}[R]_{0}=k^{\prime \prime} t \label{13.9}\]

\[[A]_{t}=[A]_{0}-k^{\prime \prime} t \label{13.10}\]

де\(k^{\prime \prime}\) = k _f [A] ₀ [R] ₀.

Сказати, що реакція є псевдо-першим порядком в А означає, що реакція поводиться так, ніби вона першого порядку в A і нульовому порядку в R, хоча основна кінетика складніша. Ми називаємо\(k^{\prime}\) постійну швидкості псевдопершого порядку. Сказати, що реакція є псевдо-нульовим порядком означає, що реакція поводиться так, ніби вона нульового порядку в A і нульовому порядку в R, хоча основна кінетика є більш складною. Ми\(k^{\prime \prime}\) називаємо постійну швидкості псевдонульового порядку.

Моніторинг реакції

Остаточна вимога полягає в тому, що ми повинні мати можливість контролювати прогрес реакції, слідуючи за зміною концентрації принаймні для одного з її видів. Який вид ми вибираємо для моніторингу, не важливий: це може бути аналіт, реагент, який реагує з аналітом, або продукт. Наприклад, ми можемо визначити концентрацію фосфату, попередньо відреагувавши його з Mo (VI) з утворенням 12-молібдофосфорної кислоти (12-МПА).

\[\mathrm{H}_{3} \mathrm{PO}_{4}(a q)+6 \mathrm{Mo}(\mathrm{VI})(a q) \longrightarrow 12-\mathrm{MPA}(a q)+9 \mathrm{H}^{+}(a q) \label{13.11}\]

Далі зменшуємо 12-МПА до гетерополіфосгомолібденового синього, ПМБ. Швидкість утворення ПМБ вимірюється спектрофотометрично і пропорційна концентрації 12-МПА. Концентрація 12-МПА, в свою чергу, пропорційна концентрації фосфату [див., наприклад, (а) Крауч, С.Р.; Malmstadt, H.V. анал. Хім. 1967, 39, 1084—1089; (б) Крауч, С.Р.; Мальмштадт, Г.В. анал. Хім. 1967, 39, 1090—1093; (c) Мальмштадт, Г.В.; Кордос, Е. Хім. 1972, 44 (12), 26—41А]. Ми також можемо стежити за реакцією 13.11 спектрофотометрично, контролюючи утворення жовтого кольору 12-МПА [Хав'єр, А.С.; Крауч, С.Р.; Мальмштадт, Н. Хім. 1969, 41, 239—243].

Реакція\ ref {13.11}, звичайно, незбалансована; додаткові водень на правій стороні реакції походять від шести Mo (VI), які з'являються на лівій стороні реакції, де вважається, що Mo (VI) присутній як димер молібдату HMO ₂ O ₆ ⁺.

Класифікація хімічних кінетичних методів

Рисунок Template:index містить одну корисну схему класифікації хімічних кінетичних методів аналізу. Методи поділяються на дві великі категорії: методи прямого обчислення та методи підгонки кривих. У методі прямого обчислення ми обчислюємо початкову концентрацію аналіта, [A] ₀, використовуючи відповідний закон швидкості. Наприклад, якщо реакція першого порядку в аналіті, ми можемо використовувати Equation\ ref {13.2} для визначення [A] ₀ заданих значень для k, t і [A] _t. За допомогою методу підгонки кривої ми використовуємо регресію, щоб знайти найкраще відповідність між даними - наприклад, [A] _t як функція часу - і відомою математичною моделлю для закону швидкості. Якщо реакція в аналіті першого порядку, то ми підставляємо Equation\ ref {13.2} до даних, використовуючи k і [A] ₀ як регульовані параметри.

Рисунок Template:index. Класифікація хімічних кінетичних методів аналізу, адаптованих з Pardue, H.L. «Кінетичні аспекти аналітичної хімії», Anal. Чим. Акт 1989, 2016, 69—107.

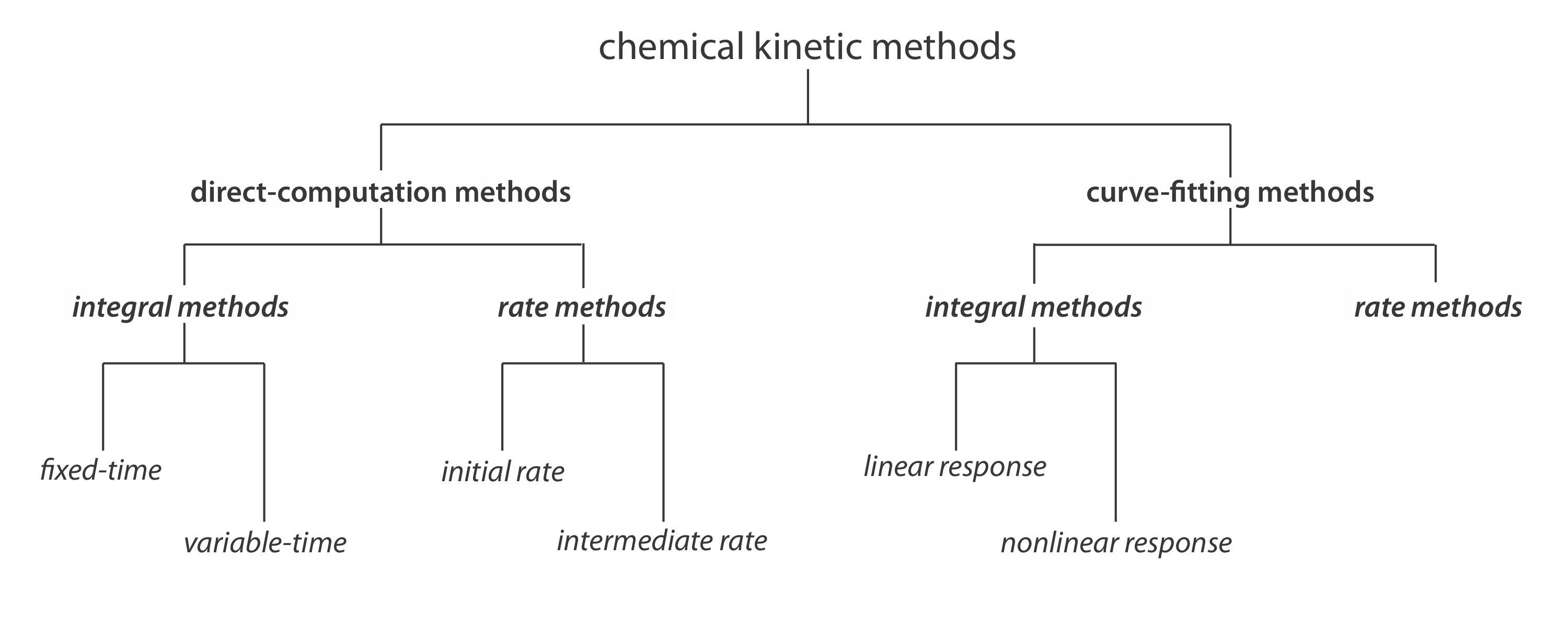
Прямі обчислення фіксованого часу інтегральних методів

Інтегральний метод прямого обчислення використовує інтегровану форму закону ставок. Наприклад, в одноточковому методі фіксованого часу ми визначаємо концентрацію аналіту за один раз і обчислюємо початкову концентрацію аналіту [A] ₀, використовуючи відповідний інтегрований закон швидкості. Для визначення константи швидкості реакції k проводимо окремий експеримент, використовуючи стандартний розчин аналіту. Крім того, ми можемо визначити початкову концентрацію аналіта шляхом вимірювання [A] _t для кількох стандартів, які містять відомі концентрації аналіту, і побудувати калібрувальну криву.

Приклад Template:index

Концентрацію нітрометану, CH ₃ NO ₂, визначають з кінетики реакції його розкладання. При наявності надлишку основи реакція є псевдо-першого порядку в нітрометані. Для стандартного розчину 0,0100 М нітрометану концентрація нітрометану через 2,00 с становить\(4.24 \times 10^{-4}\) М. При аналізі зразка, що містить невідому кількість нітрометану, концентрація нітрометану, що залишилася через 2,00 с, дорівнює\(5.35 \times10^{-4}\) М. в зразку?

Рішення

Спочатку визначаємо значення для постійної швидкості псевдопершого порядку,\(k^{\prime}\). Використовуючи Equation\ ref {13.7} і результат для стандарту, знайдемо його значення

\[k^{\prime} = \frac {\ln{[A]_0} - \ln{[A]_t}} {t} = \frac {\ln{(0.0100)} - \ln{(4.24 \times 10^{-4})}} {2.00 \text{ s}} = 1.58 \text{ s}^{-1} \nonumber\]

Далі ми використовуємо Equation\ ref {13.8} для обчислення початкової концентрації нітрометану в зразку.

\[[A]_0 = \frac {[A]_t} {e^{-k^{\prime}t}} = \frac {5.35 \times 10^{-4} \text{ M}} {e^{-(1.58 \text{ s}^{-1})(2.00 \text{ s})}} = 0.0126 \text{ M} \nonumber\]

Рівняння\ ref {13.7} та Equation\ ref {13.8} однаково відповідні інтегровані закони швидкості для реакції псевдопершого порядку. Рішення використовувати Equation\ ref {13.7} для обчислення\(k^{\prime}\) та Equation\ ref {13.8} для обчислення [A] ₀ є питанням зручності.

Вправа Template:index

В окремому визначенні для нітрометану ряд зовнішніх стандартів дає наступні концентрації нітрометану після розкладання 2,00 с в умовах псевдопершого порядку.

[СН 3 НІ 2] 0 (М)	[СН 3 НІ 2] т = 2,00 с (М)
0,0100	\(3.82 \times 10^{-4}\)
0,0200	\(8.19 \times 10^{-3}\)
0,0300	\(1.15 \times 10^{-3}\)
0,0400	\(1.65 \times 10^{-3}\)
0,0500	\(2.14 \times 10^{-3}\)
0.0600	\(2.53 \times 10^{-3}\)
0.0700	\(3.21 \times 10^{-3}\)
0.0800	\(3.35 \times 10^{-3}\)
0,0900	\(3.99 \times 10^{-3}\)
0.100	\(4.13 \times 10^{-3}\)

Аналіз зразка в тих же умовах дає концентрацію нітрометану\(2.21 \times 10^{-3}\) М через 2 с. яка початкова концентрація нітрометану в пробі?

Відповідь

Калібрувальна крива та рівняння калібрування для зовнішніх стандартів наведені нижче. Підстановка\(2.21 \times 10^{-3}\) М на [CH ₃ NO ₂] _{t = 2s} дає [CH ₃ NO ₂] ₀ як\(5.21 \times 10^{-2}\) M.

У прикладі Template:index ми визначаємо початкову концентрацію аналіту шляхом вимірювання кількості аналіту, який не відреагував. Іноді зручніше виміряти концентрацію реагенту, який вступає в реакцію з аналітом, або виміряти концентрацію одного з продуктів реакції. Ми можемо використовувати одноточковий інтегральний метод з фіксованим часом, якщо ми знаємо стехіометрію реакції. Наприклад, якщо виміряти концентрацію продукту, Р, в реакції

\[A+R \rightarrow P \nonumber\]

то концентрація аналіта в той час t

\[[A]_{t}=[A]_{0}-[P]_{t} \label{13.12}\]

тому що стехіометрія між аналітом і продуктом становить 1:1. Якщо реакція псевдо-першого порядку в A, то підстановка Equation\ ref {13.12} на Рівняння\ ref {13.7} дає

\[\ln \left([A]_{0}-[P]_{t}\right) = \ln{[A]_{0}} - k^{\prime} t \label{13.13}\]

який ми спрощуємо, написавши в експоненціальній формі.

\[[A]_0 - [P]_t = [A]_0 e^{-k^{\prime}t} \label{13.14}\]

Нарешті, розв'язування рівняння\ ref {13.14} для [A] ₀ дає наступне рівняння.

\[[A]_{0}=\frac{[P]_{t}}{1-e^{-k^{\prime}t}} \label{13.15}\]

Приклад Template:index

Концентрацію тіоцианату, SCN ^—, визначають з псевдо-кінетики його реакції з надлишком Fe ^{3 +} з утворенням червонуватого кольору комплексу Fe (SCN) ²⁺. Прогрес реакції контролюється шляхом вимірювання поглинання Fe (SCN) ²⁺ на довжині хвилі 480 нм. При застосуванні стандартного розчину 0,100 М SCN ^— концентрація Fe (SCN) ²⁺ через 10 с становить 0,0516 м Концентрація Fe (SCN) ²⁺ в зразку, що містить невідому кількість SCN ^— становить 0,0420 М через 10 с. ^— в зразку?

Рішення

По-перше, ми повинні визначити значення для псевдо-першого порядку постійної швидкості,\(k^{\prime}\). Використовуючи Equation\ ref {13.13}, ми знаходимо, що його значення

\[k^{\prime} = \frac{\ln{[A]_{0}} - \ln \left([A]_{0} - [P]_{1}\right)}{t}= \frac {\ln(0.100) - \ln(0.100 - 0.0516)} {10.0 \text{ s}} = 0.0726 \text{ s}^{-1} \nonumber\]

Далі ми використовуємо Equation\ ref {13.15} для визначення початкової концентрації SCN ^— у зразку.

\[[A]_{0}=\frac{[P]_{t}}{1-e^{-k^{\prime} t}}=\frac{0.0420 \mathrm{M}}{1-e^{-\left(0.0726 \text{ s}^{-1}\right)(10.0 \text{ s})}}=0.0868 \mathrm{M} \nonumber\]

Вправа Template:index

В окремому визначенні для SCN ^— серія зовнішніх стандартів дає наступні концентрації Fe (SCN) ²⁺ після реакції 10,0 с із надлишком Fe ^{3 +} в умовах псевдопершого порядку.

[СКН ^-] (М)	[Fe (СКН) ^2+] т = 10,0 с (М)
\(5.00 \times 10^{-3}\)	\(1.79 \times 10^{-3}\)
\(1.50 \times 10^{-2}\)	\(8.24 \times 10^{-3}\)
\(2.50 \times 10^{-2}\)	\(1.28 \times 10^{-2}\)
\(3.50 \times 10^{-2}\)	\(1.85 \times 10^{-2}\)
\(4.50 \times 10^{-2}\)	\(2.21 \times 10^{-2}\)
\(5.50 \times 10^{-2}\)	\(2.81 \times 10^{-2}\)
\(6.50 \times 10^{-2}\)	\(3.27 \times 10^{-2}\)
\(7.50\times 10^{-2}\)	\(3.91 \times 10^{-2}\)
\(8.50 \times 10^{-2}\)	\(4.23 \times 10^{-2}\)
\(9.50 \times 10^{-2}\)	\(4.89 \times 10^{-2}\)

Аналіз зразка за тих же умов дає Fe (SCN) ²⁺ концентрацію\(3.52 \times 10^{-2}\) M через 10 с Яка початкова концентрація SCN ^— у зразку?

Відповідь

Калібрувальна крива та рівняння калібрування для зовнішніх стандартів наведені нижче. Заміна\(3.52 \times 10^{-2}\) M на [Fe (SCN) ²⁺] _{t = 10 с} дає [SCN ^—] ₀ як\(6.87 \times 10^{-2}\) M.

Одноточковий інтегральний метод з фіксованим часом має перевагу простоти, оскільки нам потрібно лише одне вимірювання для визначення початкової концентрації аналіта. Як і будь-який метод, який спирається на єдине визначення, одноточковий інтегральний метод з фіксованим часом не може компенсувати постійну детермінантну похибку. У двоточковому методі фіксованого часу ми коректуємо постійні детермінантні похибки шляхом проведення вимірювань у двох точках часу та використовуємо різницю між вимірами для визначення початкової концентрації аналіту. Оскільки це впливає на обидва вимірювання однаково, різниця між вимірами не залежить від постійної помилки припинення. Для реакції псевдопершого порядку, в якій ми вимірюємо концентрацію аналіта в рази t ₁ і t ₂, ми можемо записати наступні два рівняння.

\[[A]_{t_{1}}=[A]_{0} e^{-k^{\prime} t_1} \label{13.16}\]

\[[A]_{t_{2}}=[A]_{0} e^{-k^{\prime} t_2} \label{13.17}\]

Віднімання рівняння\ ref {13.17} з рівняння\ ref {13.16} та розв'язування для [A] ₀ залишає нам

\[[A]_{0}=\frac{[A]_{t_1}-[A]_{t_2}}{e^{-k^{\prime} t_{1}}-e^{-k^{\prime} t_{2}}} \label{13.18}\]

Щоб визначити константу швидкості\(k^{\prime}\), виміряємо\([A]_{t_1}\) і\([A]_{t_2}\) для стандартного розчину аналіту. Отримавши значення для\(k^{\prime}\), ми можемо визначити [А] ₀ шляхом вимірювання концентрації аналіта при t ₁ і t ₂. Ми також можемо визначити початкову концентрацію аналіта за допомогою калібрувальної кривої, що складається з графіка (\([A]_{t_1}\)—\([A]_{t_2}\)) проти [A] ₀.

Інтегральний метод із фіксованим часом особливо корисний, коли сигнал є лінійною функцією концентрації, оскільки ми можемо замінити концентрацію реагенту відповідним сигналом. Наприклад, якщо ми стежимо за реакцією спектрофотометрично в умовах, коли концентрація аналіта підпорядковується закону Беера

\[(A b s)_{t}=\varepsilon b[A]_{t} \nonumber\]

тоді ми можемо переписати рівняння\ ref {13.8} і рівняння\ ref {13.18} як

\[(A b s)_{t}=[A]_{0} e^{-k^{\prime}} \varepsilon b=c[A]_{0} \nonumber\]

\[[A]_t = \frac {(Abs)_{t_1} - (Abs)_{t_2}} {e^{-k^{\prime}t_1} - e^{-k^{\prime}t_2}} \times (\epsilon b)^{-1} = c^{\prime}[(Abs)_{t_1} - (Abs)_{t_2}] \nonumber\]

де (Abs) _t - поглинання в момент t, а c і\(c^{\prime}\) є константами.

Прямі обчислення змінно-часу інтегральні методи

В інтегральному методі змінного часу вимірюється сумарний час\(\Delta_t\), необхідний для здійснення конкретної зміни концентрації для одного виду в хімічній реакції. Одним з важливих застосувань є кількісний аналіз каталізаторів, який використовує перевагу здатності каталізатора збільшувати швидкість реакції. Зі збільшенням концентрації каталізатора\(\Delta_t\) зменшується. Для багатьох каталітичних систем взаємозв'язок між концентрацією каталізатора\(\Delta_t\) та концентрацією

\[\frac {1} {\Delta t} = F_{cat}[A]_0 + F_{uncat} \label{13.19}\]

де [A] ₀ - концентрація каталізатора, а F _cat і F _uncat - константи, що складають швидкість каталізованої і некаталізованої реакцій [Mark, H. B.; Rechnitz, G. Кінетика в аналітичній хімії, Міжнаукові: Нью-Йорк, 1968].

Приклад Template:index

Санделл і Кольтофф розробили кількісний метод йодиду, заснований на його здатності каталізувати наступну окислювально-відновну реакцію [Санделл, Е. Б.; Колтофф, І.М. Хім. Соц. 1934, 56, 1426].

\[\mathrm{As}^{3+}(a q)+2 \mathrm{Ce}^{4+}(a q) \longrightarrow \mathrm{As}^{\mathrm{5+}}(a q)+2 \mathrm{Ce}^{3+}(a q) \nonumber\]

Криву калібрування зовнішніх стандартів готували шляхом додавання 1 мл стандарту KI до суміші 2 мл 0,05 М As ^{3 +}, 1 мл 0,1 M Ce ^{4 +}, 1 мл 3 M H 2 SO 4 і 1 мл 3 M H ₂ SO ₄, і вимірювання часу для жовтого кольору Ce ^{4 +} зникнути. Наступна таблиця підсумовує результати для одного аналізу.

[I ^-] (мкг/мл)	\(\Delta_t\)(хв)
5.0	\ (\ Дельта_T\) (хв) ">0.9
2.5	\ (\ Дельта_т\) (хв) ">1.8
1.0	\ (\ Дельта_т\) (хв) ">4.5

Яка концентрація I ^— у пробі, якщо\(\Delta_t\) становить 3,2 хв?

Рішення

На малюнку Template:index показано калібрувальну криву та калібрувальне рівняння для зовнішніх стандартів на основі Equation\ ref {13.19}. Заміна 3,2 хв на\(\Delta_t\) дає концентрацію I ^— у зразку як 1,4 мкг/мл.

Рисунок Template:index. Калібрувальна крива і калібрування рівняння для Приклад 13.2.3.

Методи прямого обчислення швидкості

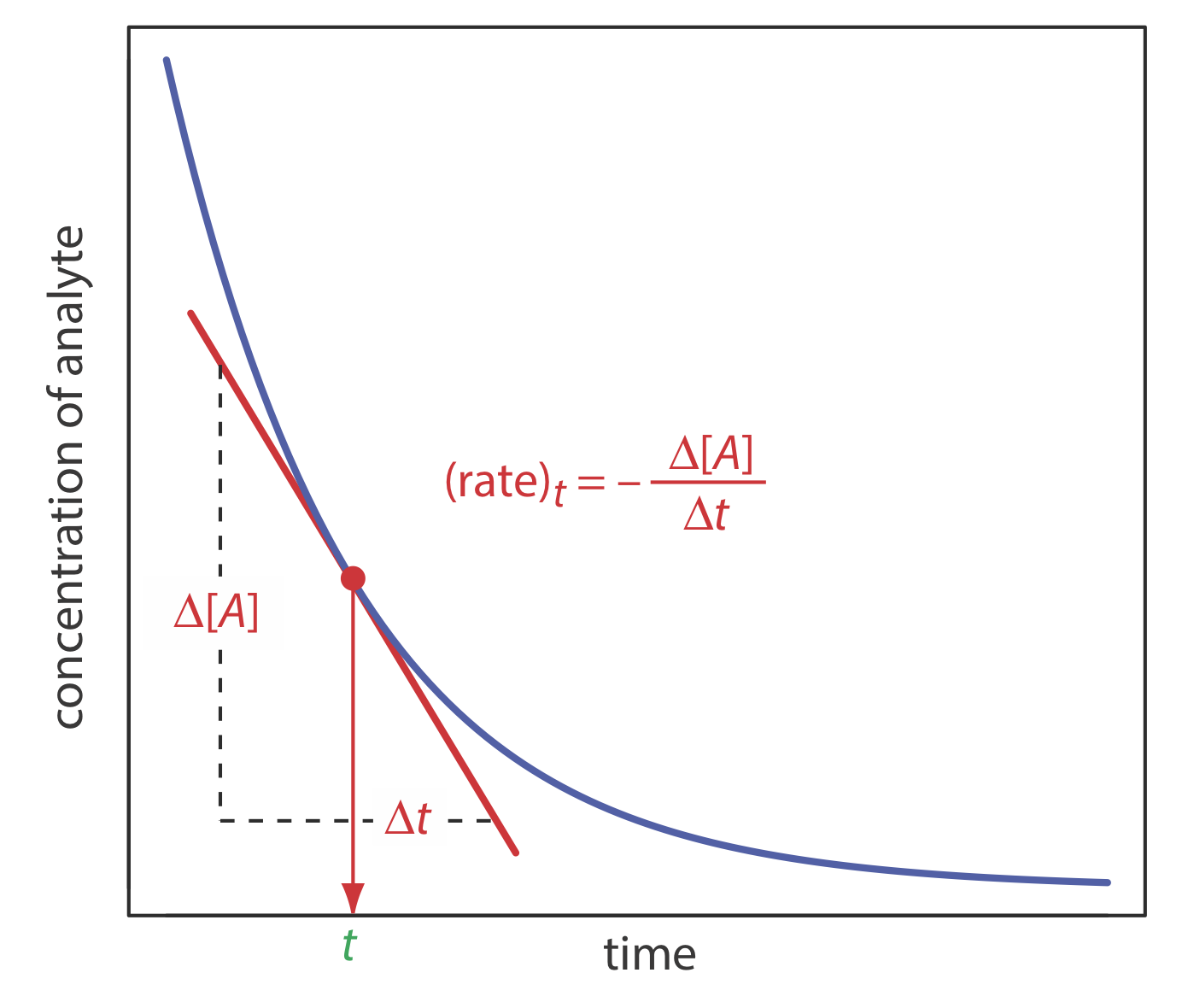
Для визначення концентрації аналіта в методі швидкості використовується диференціальна форма закону швидкості — рівняння\ ref {13.1} є одним із прикладів закону диференціальної швидкості. Як показано на малюнку Template:index, швидкість реакції в момент t, (швидкість) _t - це нахил прямої дотичної до кривої, яка показує зміну концентрації в залежності від часу. Для реакції, яка є першим порядком в аналіті, швидкість в той час це

\[(r a t e)_{t}=k[A]_{t} \nonumber\]

Підстановка в Equation\ ref {13.3} залишає нам наступне рівняння, що пов'язує швидкість часу t до початкової концентрації аналіта.

\[(\text {rate})_{t}=k[A]_{0} e^{-k t} \nonumber\]

Якщо виміряти швидкість у фіксований час, то і k, і e ^{— kt} є постійними, і ми можемо використовувати калібрувальну криву (швидкість) _t проти [A] ₀ для кількісного аналізу аналіт.

Рисунок Template:index. Визначення миттєвої швидкості реакції за час t від нахилу дотичної прямої до кривої, яка показує зміну концентрації аналіта як функції часу.

Є кілька переваг використання початкової швидкості реакції (t = 0). По-перше, оскільки швидкість реакції зменшується з часом, початкова швидкість забезпечує найбільшу чутливість. По-друге, оскільки початкова швидкість вимірюється в умовах майже псевдонульового порядку, в яких зміна концентрації з часом ефективно лінійна, легше визначити нахил. Нарешті, у міру прогресування реакції інтересу можуть розвиватися конкуруючі реакції, які ускладнюють кінетику: використання початкової швидкості усуває ці ускладнення. Одним з недоліків методу початкової швидкості є те, що може бути недостатньо часу для повного змішування реагентів. Цю проблему можна уникнути, використовуючи проміжний показник, виміряний пізніше (t > 0).

Як загальне правило (див. Mottola, H.A. «Кінетичні визначення реагентів, що використовують некаталізовані реакції,» Анальний. Чим. Acta 1993, 280, 279—287), час вимірювання початкової швидкості реакції має призвести до споживання не більше 2% реагентів. Чим менше цей відсоток, тим лінійніше зміна концентрації в залежності від часу.

Приклад Template:index

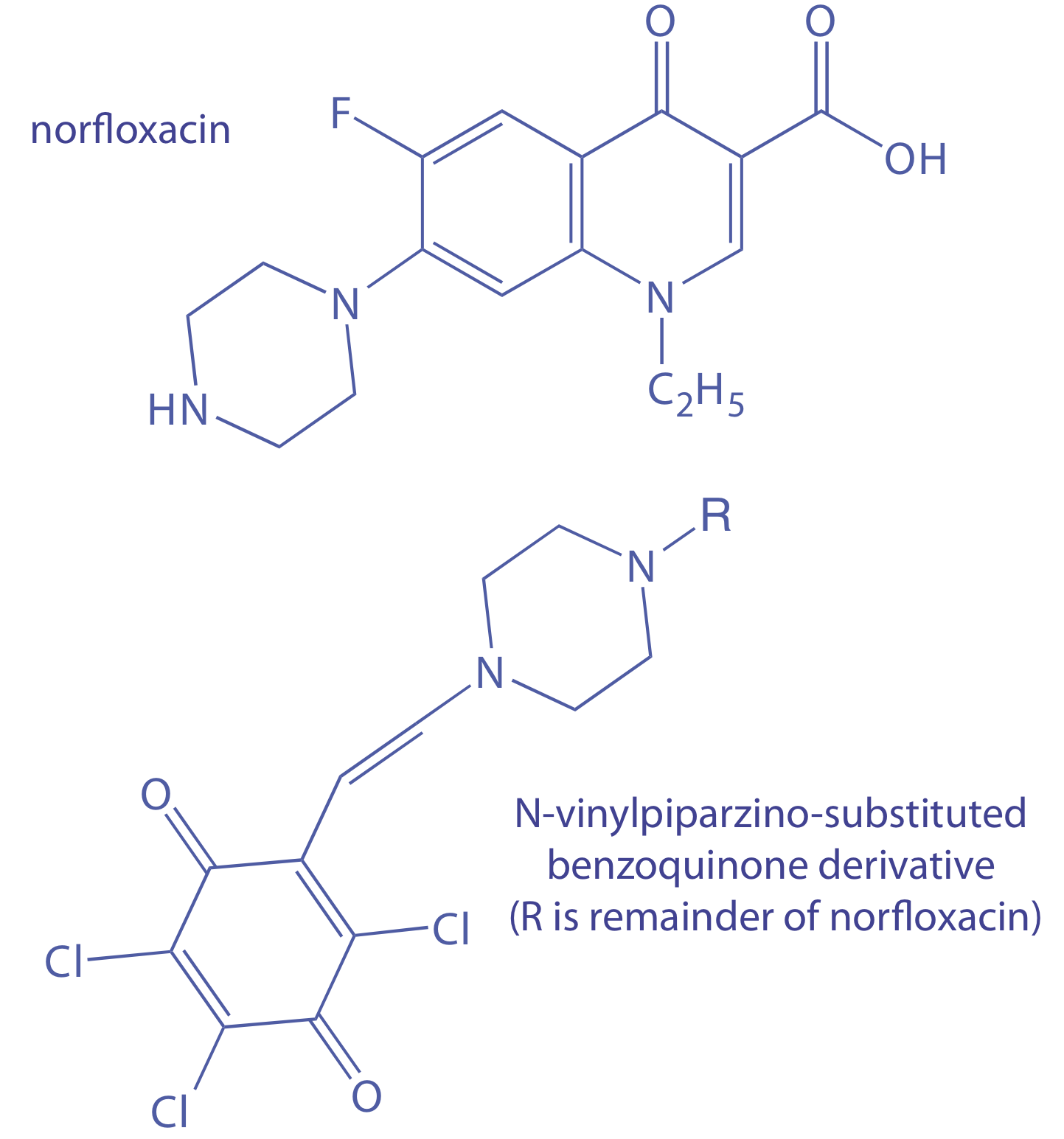
Концентрація норфлоксацину, зазвичай призначається антибактеріального засобу, визначається методом початкової норми. Норфлоксацин перетворюється на похідне N-вінілпіперазину і реагував з 2,3,5,6-тетра-хлор-1,4-бензохіноном з утворенням N-вінілпіперазино-заміщеного похідного бен-зохінону, яке сильно поглинається при 625 нм [Дарвіш, І.А.; Султан, М. 78, 1383—1388]. Початкова швидкість реакції - як вимірюється зміною поглинання як функція часу (AU/хв) - є псевдо-першим порядком у норфлоксацину. Наступні дані були отримані для ряду зовнішніх стандартів норфлоксацину.

[норфлоксацин] (мкг/мл)	початкова швидкість (AU/хв)
63	0.0139
125	0.0355
188	0.0491
251	0.0656
313	0.0859

Для аналізу зразка рецептурних очних крапель порцію 10,00 мл екстрагують дихлорметаном. Екстракт висушують і відновлюють норфлоксацин в метанолі і розводять до 10 мл у об'ємній колбі. 5,00-мл порцію цього розчину розводять до обсягу в об'ємній колбі об'ємом 100 мл. Аналіз цієї вибірки дає початкову швидкість 0,0394 аУ/хв.

Яка концентрація норфлоксацину в очних краплях в мг/мл?

Рішення

На малюнку Template:index показано калібрувальну криву та рівняння калібрування для зовнішніх стандартів. Заміна 0,0394 ау/хв на початкову швидкість і розчинивши для концентрації норфлоксацину дає результат 152 мкг/мл. Це концентрація в розведеному зразку екстракту. Концентрація в екстракті перед розведенням становить

\[\frac{152 \: \mu \text{g}}{\mathrm{mL}} \times \frac{100.0 \: \mathrm{mL}}{5.00 \: \mathrm{mL}} \times \frac{1 \:\mathrm{mg}}{1000 \: \mu \mathrm{g}}=3.04 \: \mathrm{mg} / \mathrm{mL} \nonumber\]

Оскільки сушений екстракт був відновлений за допомогою обсягу, ідентичного вихідному зразку, концентрація норфлоксацину в очних краплях становить 3,04 мг/мл.

Рисунок Template:index. Калібрувальна крива та калібрувальне рівняння для Приклад Template:index.

Методи підгонки кривої

У методі прямого обчислення ми визначаємо концентрацію аналіта шляхом вирішення відповідного рівняння швидкості в один-два дискретних рази. Зв'язок між концентрацією аналіта і виміряної відгуком - це функція константи швидкості, яку ми визначаємо в окремому експерименті за допомогою єдиного зовнішнього стандарту (див. Приклад 13.2.1 або Приклад 13.2.2), або калібрувальної кривої (див. Приклад 13.2.3 або приклад 13.2.4).

У методі підгонки кривої ми постійно контролюємо концентрацію реагенту або продукту як функцію часу і використовуємо регресійний аналіз, щоб пристосувати дані до відповідного закону диференціальної швидкості або інтегрованого закону швидкості. Наприклад, якщо ми відстежуємо концентрацію продукту для реакції, яка є псевдо-першого порядку в аналіті, то ми можемо пристосувати дані до наступної переставленої форми Equation\ ref {13.15}

\[[P]_{t}=[A]_{0}\left(1-e^{-k^{\prime} t}\right) \nonumber\]

використовуючи [A] ₀ і\(k^{\prime}\) як регульовані параметри. Оскільки ми використовуємо дані з більш ніж одного або двох дискретних разів, метод підгонки кривої здатний дати більш надійні результати.

Приклад Template:index

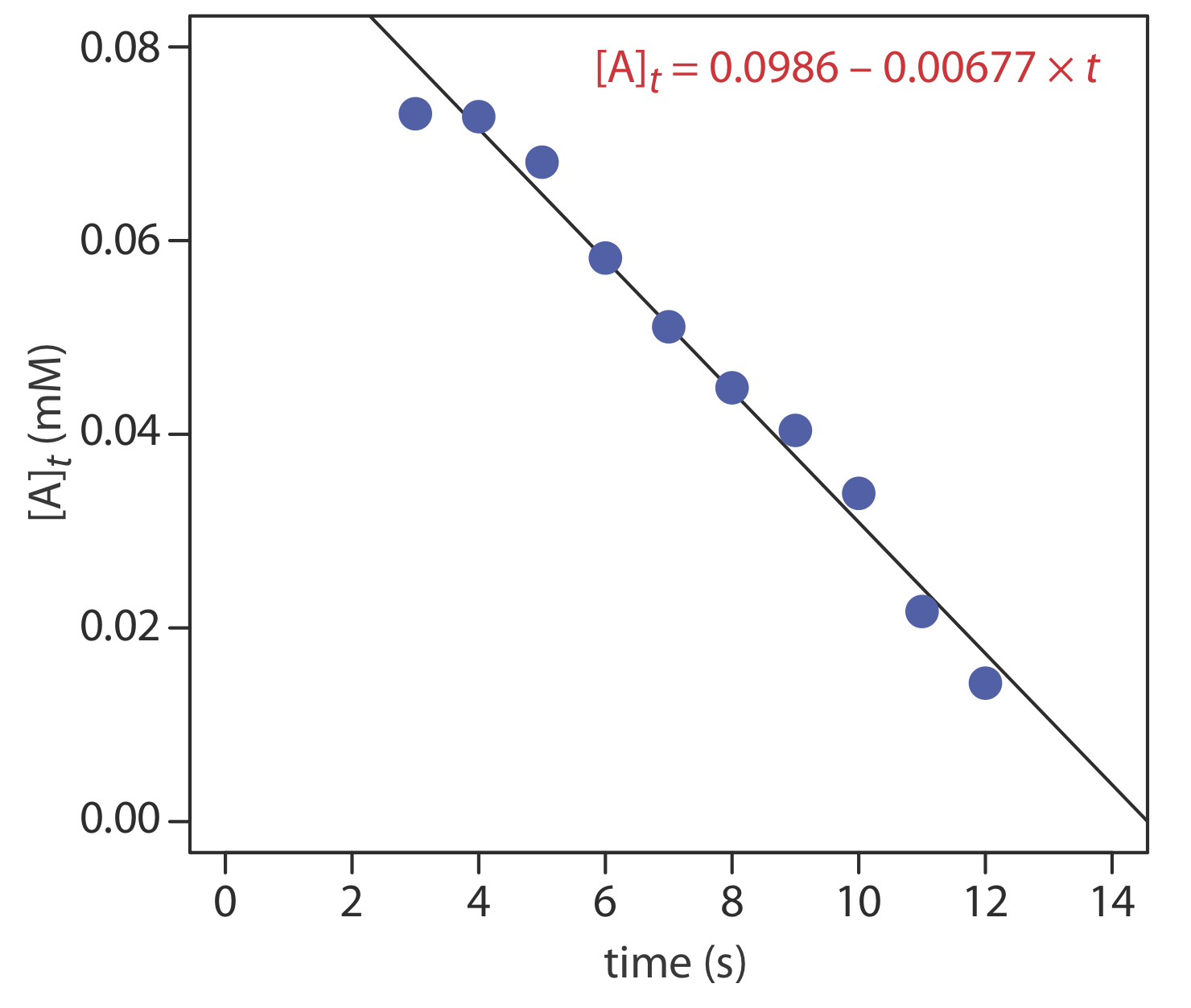
Дані, наведені в наступній таблиці, були зібрані для реакції, яка, як відомо, є псевдонульовим порядком в аналіті. Яка початкова концентрація аналіту в пробі і постійна швидкості для реакції?

час (и)	[А] т (мМ)	час (и)	[А] т (мМ)
3	0.0731	8	0.0448
4	0.0728	9	0.0404
5	0.0681	10	0.0339
6	0.0582	11	0.0217
7	0.0511	12	0.0143

Рішення

З Equation\ ref {13.10} ми знаємо, що для реакції псевдонульового порядку графік [A] _t проти часу є лінійним з нахилом\(-k^{\prime \prime}\) і y -перехопленням [A] ₀. Рисунок Template:index показує графік кінетичних даних і результат лінійного регресійного аналізу. Початкова концентрація аналіту становить 0,0986 мМ, а константа швидкості 0,00677 М ^—1 с ^—1.

Рисунок Template:index. Результат підгонки рівняння\ ref {13.10} до даних у прикладі Template:index.

Найкращий спосіб оцінити теоретичні та практичні деталі, розглянуті в цьому розділі, - це уважно вивчити типовий аналітичний метод. Хоча кожен метод унікальний, наступний опис визначення креатиніну в сечі дає повчальний приклад типової процедури. Опис тут базується на Diamandis, E.P.; Koupparis, M.A.; Hadjioannou, T P. «Кінетичні дослідження з іонно-селективними електродами: визначення креатиніну в сечі за допомогою пікратного іонного селективного електрода», J. Chem. Едук. 1983, 60, 74—76.

Представницький метод 13.2.1: Визначення креатиніну в сечі

Опис методу

Креатин - це органічна кислота в м'язовій тканині, яка постачає енергію для м'язових скорочень. Одним з продуктів його обміну є креатинін, який виводиться з сечею. Оскільки концентрація креатиніну в сечі і сироватці крові є важливим показником функції нирок, швидкий метод його аналізу має клінічно важливе значення. При цьому методі швидкість реакції між креатиніну і пікратом в лужному середовищі використовується для визначення концентрації креатиніну в сечі. В умовах аналізу реакція першого порядку на пітрат, креатинін та гідроксид.

\[\text { rate }=k[\text { picrate }][\text { creatinine }]\left[\mathrm{OH}^{-}\right] \nonumber\]

Реакція контролюється за допомогою пітратного іонно-селективного електрода.

Порядок дій

Готують комплекс зовнішніх стандартів, які містять 0,5-3,0 г/л креатиніну, використовуючи вихідний розчин 10,00 г/л креатиніну в 5 мМ Н ₂ SO ₄, розводячи кожен стандарт до обсягу за допомогою 5 мМ H ₂ SO ₄. Приготуйте розчин\(1.00 \times 10^{-2}\) М пітрату натрію. Піпет 25,00 мл 0,20 М NaOH, відрегульований до іонної сили 1,00 М за допомогою Na ₂ SO ₄, в термостатичну реакційну клітину при 25 ^o С. Додати 0,500 мл розчину\(1.00 \times 10^{-2}\) М пірату в реакційну клітину. Призупиніть селективний пікрат-іон у розчині та контролюйте потенціал, поки він не стабілізується. Коли потенціал стабільний, додайте 2,00 мл зовнішнього стандарту креатиніну і запишіть потенціал як функцію часу. Повторіть цю процедуру, використовуючи інші зовнішні стандарти. Побудувати калібрувальну криву\(\Delta E / \Delta t\) проти початкової концентрації креатиніну. Використовуйте ту ж процедуру для аналізу зразків, використовуючи 2,00 мл сечі замість зовнішнього стандарту. Визначте концентрацію креатиніну в зразку за допомогою калібрувальної кривої.

Питання

1. Аналіз проводиться в умовах, які знаходяться в псевдо-першому порядку в пікраті. Показати, що за цих умов зміна потенціалу як функція часу є лінійною.

Потенціал Е пітратного іонно-селективного електрода задається рівнянням Нернста

\[E=K-\frac{R T}{F} \ln{[\text { picrate }]} \nonumber\]

де K - константа, яка припадає на опорні електроди, потенціали переходу та потенціал асиметрії іонно-селективного електрода, R - газова константа, T - температура, а F - постійна Фарадея. З рівняння\ ref {13.7} відомо, що для реакції псевдо-першого порядку концентрація пірату в момент t дорівнює

\[\ln {[\text{picrate}]_t}=\ln{[\text {picrate}]}_{0}-k^{\prime} t \nonumber\]

де\(k^{\prime}\) - постійна швидкості псевдопершого порядку. Заміна цього інтегрованого закону швидкості в іонно-селективне електродне рівняння Нернста залишає нам наступний результат.

\[E_{t} = K - \frac{R T} {F} \left( \ln{[\text {picrate}]}_{0} - k^{\prime} t\right) \nonumber\]

\[E_{t} = K - \frac{R T} {F} \ln{[\text {picrate}]}_{0} + \frac{R T} {F} k^{\prime}t \nonumber\]

Оскільки K і (RT/F) ln [picrate] ₀ є константами, ділянка E _t проти t є прямою лінією з нахилом\(\frac{R T} {F} k^{\prime}\).

2. В умовах аналізу швидкість реакції псевдопершого порядку в пітраті і псевдо-нульового порядку в креатиніні і ОН ^—. Поясніть, чому можна підготувати калібрувальну криву\(\Delta E / \Delta t\) проти концентрації креатиніну.

Нахил ділянки E _{t проти t} дорівнює\(\Delta E / \Delta t = RTk^{\prime}/F\) = RTK ′/ F (див. попереднє питання). Оскільки реакція проводиться в умовах, коли вона є псевдонульовим порядком в креатиніні і ОН ^-, закон швидкості є

\[\text{rate} = k[\text{picrate}][\text{creatinine}]_0[\text{OH}^-]_0 = k^{\prime}[\text{picrate}] \nonumber\]

Постійна швидкості псевдопершого порядку\(k^{\prime}\),,

\[k^{\prime}=k[\text { creatinine }]_{0}\left[\mathrm{OH}^{-}\right]_{0}=c[\text {creatinine}]_{0} \nonumber\]

де c - константа, еквівалентна k [OH ^-] ₀. Отже, нахил ділянки E _t проти t є лінійною функцією початкової концентрації креатиніну

\[\frac{\Delta E}{\Delta t}=\frac{R T k^{\prime}}{F}=\frac{R T c}{F}[\text {creatinine}]_{0} \nonumber\]

а ділянка\(\Delta E / \Delta t\) проти концентрації креатиніну може служити калібрувальною кривою.

3. Навіщо потрібна терморегуляція реакційної клітини?

Швидкість реакції залежить від температури. Реакційна комірка термостатирована для підтримки постійної температури, щоб запобігти визначеній похибці від систематичної зміни температури та мінімізувати невизначені помилки від випадкових коливань температури.

4. Чому необхідно готувати розчин NaOH, щоб він мав іонну міцність 1,00 М?

Потенціал селективного електрода пікрат-іонів фактично реагує на активність пітратного аніону в розчині. Регулюючи розчин NaOH до високої іонної сили, ми підтримуємо постійну іонну силу у всіх стандартах та зразках. Оскільки зв'язок між активністю та концентрацією є функцією іонної сили, використання постійної іонної сили дозволяє нам писати рівняння Нернста з точки зору концентрації пірату замість його активності.

Виконання кінетичних вимірювань

При використанні репрезентативного методу 13.2.1 для визначення концентрації креатиніну в сечі стежимо за кінетикою реакцій за допомогою іоноселективного електрода. В принципі, ми можемо використовувати будь-який з аналітичних методів у розділах 8—12, щоб слідувати кінетиці реакції за умови, що реакція не протікає в помітній мірі протягом часу, необхідного для вимірювання. Як і слід було очікувати, ця вимога ставить серйозне обмеження на кінетичні методи аналізу. Якщо кінетика реакції повільна щодо часу аналізу, то ми можемо зробити вимірювання без того, щоб аналіт зазнав значної зміни концентрації. Якщо швидкість реакції занадто швидка - що часто буває - тоді ми вводимо значну помилку, якщо наш час аналізу занадто довгий.

Одним з рішень цієї проблеми є зупинка, або гасіння реакції шляхом коригування експериментальних умов. Наприклад, багато реакцій показують сильну залежність від рН і гасяться додаванням сильної кислоти або міцної основи. Рисунок Template:index показує типовий приклад для ферментативного аналізу р -нітрофенілфосфату, який використовує фермент кислої фосфатази зародків пшениці для гідролізу аналіту до р -нітрофенолу. Реакція має максимальну швидкість при рН 5. Підвищення рН шляхом додавання NaOH гасить реакцію і перетворює безбарвний р -нітрофенол в жовтого кольору р -нітрофенолат, який поглинається при 405 нм.

Рисунок Template:index. Початкова норма для ферментативного гідролізу р -нітрофенілфосфату з використанням кислої фосфатази зародків пшениці. Підвищення рН гасить реакцію і приховує безбарвний р -нітрофенол до р -нітрофенолату жовтого кольору, який поглинається при 405 нм.

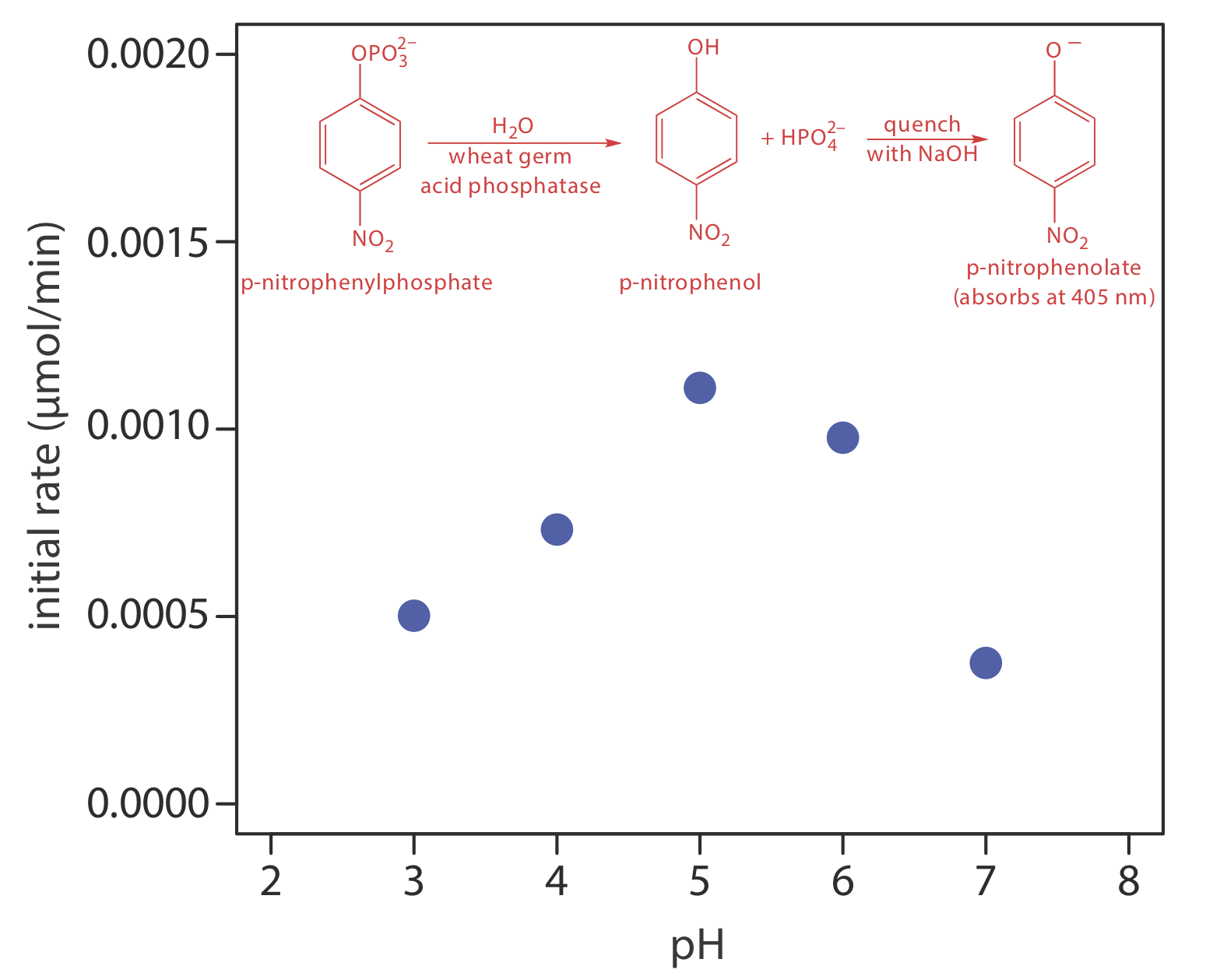
Додатковою проблемою, коли кінетика реакції швидка, є забезпечення швидкого та відтворюваного змішування зразка та реагентів. Для швидкої реакції нам потрібно провести вимірювання протягом декількох секунд - або навіть декількох мілісекунд - об'єднання зразка та реагентів. Це представляє нам проблему та перевагу. Проблема полягає в тому, що для швидкого і відтворюваного змішування зразка і реагенту потрібен спеціальний інструмент, який додає додаткових витрат на аналіз. Перевага полягає в тому, що швидкий автоматизований аналіз дозволяє забезпечити високу пропускну здатність зразків. Прилади для автоматизованого кінетичного аналізу фосфатів за допомогою реакції\ ref {13.11}, наприклад, мають швидкість відбору проб приблизно 3000 визначень на годину.

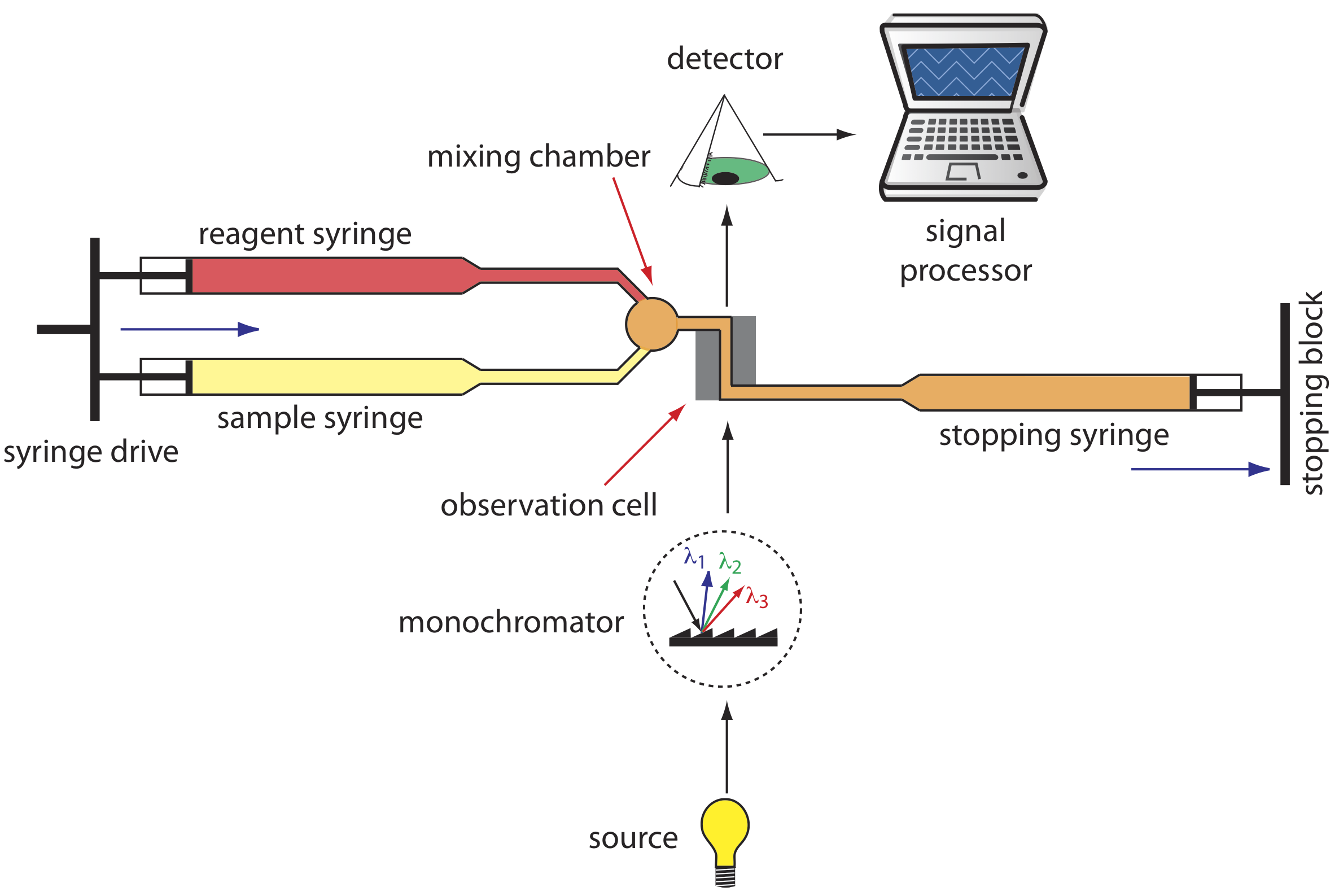
Розроблено безліч приладів для автоматизації кінетичного аналізу швидких реакцій. Одним із прикладів, який показано на рисунку Template:index, є аналізатор зупиненого потоку. Пробу і реагенти завантажують в окремі шприци і точно виміряні обсяги дозують в змішувальну камеру під дією привода шприца. Продовження дії приводу шприца виштовхує суміш через спостережну комірку і в стопорний шприц. Протитиск, що утворюється при попаданні стопорного шприца на зупинний блок, завершує змішування, після чого хід реакції контролюється спектрофотометрично. За допомогою аналізатора зупиненого потоку можна завершити змішування зразка та реагенту та ініціювати кінетичні вимірювання приблизно за 0,5 мс. Прикріпивши автопробовідбірник до шприца для зразків, можна аналізувати до декількох сотень зразків на годину.

Рисунок Template:index. Принципова схема аналізатора зупиненого потоку. Синіми стрілками показано напрямок, в якому рухаються шприци.

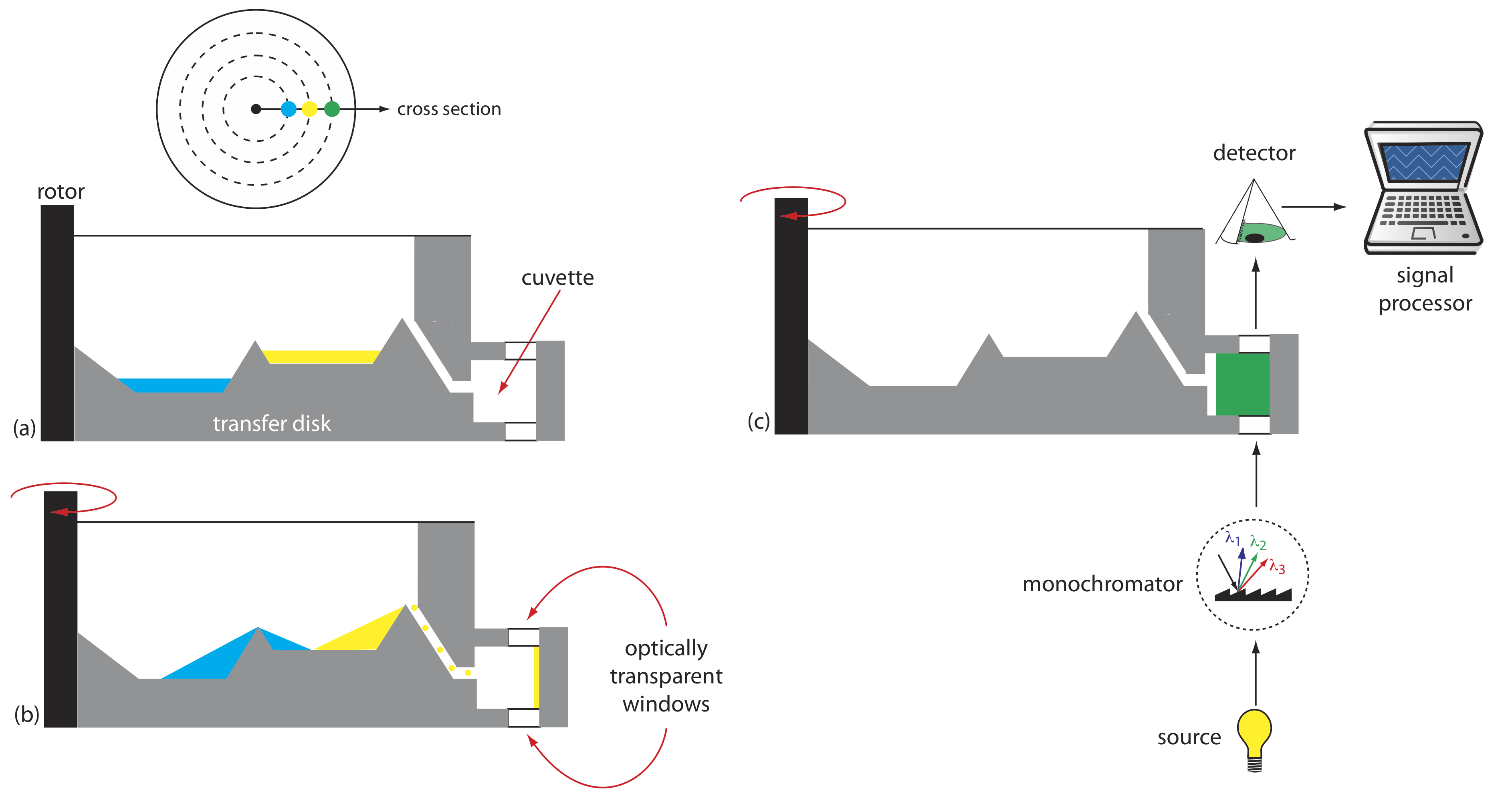
Іншим інструментом для кінетичних вимірювань є відцентровий аналізатор, частковий переріз якого наведено на малюнку Template:index. Зразок і реагенти поміщають в окремі свердловини, які орієнтовані радіально навколо кругового передавального диска. Коли центрифуга обертається, відцентрова сила тягне зразок та реагенти в кювету, де відбувається змішування. Одне оптичне джерело і детектор, розташовані нижче і над зовнішнім краєм передавального диска, вимірюють поглинання кожного разу, коли кювета проходить через оптичний промінь. При використанні передавального диска з 30 кюветами і обертається зі швидкістю 600 об/хв, ми можемо збирати 10 точок даних в секунду для кожного зразка.

Рисунок Template:index. Поперечні перерізи через відцентровий аналізатор, що показує (а) свердловини, які утримують зразок та реагенти, (б) змішування зразка та реагентів, і (в) конфігурацію спектрофотометричного детектора.

Можливість збирати багато даних і швидко їх збирати вимагає відповідного обладнання та програмного забезпечення. Не дивно, що автоматизовані кінетичні аналізатори розробляються паралельно з досягненнями аналогових та цифрових схем - апаратного забезпечення та комп'ютерного програмного забезпечення для згладжування, інтеграції та диференціації аналітичного сигналу. Для раннього обговорення важливості апаратного та програмного забезпечення див Мальмштадт, HV; Delaney, C J; Cordos, EA «Інструменти для визначення ставок» Anal. Хім. 1972, 44 (12), 79—89А.

Кількісні програми

Хімічні кінетичні методи аналізу продовжують знаходити застосування для аналізу різноманітних аналітів, особливо в клінічних лабораторіях, де автоматизовані методи допомагають обробляти великий обсяг зразків. У цьому розділі ми розглянемо кілька загальних кількісних застосувань.

Ферментно-каталізовані реакції

Ферменти є високоспецифічними каталізаторами біохімічних реакцій, причому кожен фермент демонструє селективність для одного реагенту або субстрату. Наприклад, фермент ацетилхолінестераза каталізує розкладання нейромедіатора ацетилхоліну на холін і оцтову кислоту. Багато реакцій фермент—субстрат слідують простому механізму, який складається з початкового формування комплексу фермент—субстрат, ES, який згодом розкладається з утворенням продукту, вивільняючи фермент знову реагувати.

\ [E + S\ нижня {k_ {-1}} {\ stackrel {k_1} {\ правий лівий гарпуни}} ES\ нижня {k_ {-2}} {\ stackrel {k_2} {\ rightleftharpoons}}} + P
\ етикетка {13.20}\]

де k ₁, k _—1, k ₂, а k _{—2 -} константи швидкості. Якщо зробити вимірювання на початку реакції, концентрація продуктів незначна, і ми можемо ігнорувати крок, описаний постійною швидкості k _—2. У цих умовах швидкість реакції становить

\[\text { rate }=\frac{d[P]}{d t}=k_{2}[E S] \label{13.21}\]

Щоб бути аналітично корисним, нам потрібно написати Equation\ ref {13.21} через концентрації ферменту, E, і субстрату, S. Для цього використовується стаціонарне наближення, в якому ми припускаємо, що концентрація ЕС залишається по суті постійною. Після початкового періоду, протягом якого спочатку утворюється комплекс фермент—субстрат, швидкість, з якою утворюється ЕС

\[\frac{d[E S]}{d t}=k_{1}[E][S]=k_{1}\left([E]_{0}-[E S]\right)[S] \label{13.22}\]

дорівнює швидкості, з якою вона зникає

\[-\frac{d[E S]}{d t}=k_{-1}[E S]+k_{2}[E S] \label{13.23}\]

де [E] ₀ - початкова концентрація ферменту. Поєднання рівняння\ ref {13.22} та рівняння\ ref {13.23} дає

\[k_{1}\left([E]_{0}-[E S]\right)[S]=k_{-1}[E S]+k_{2}[E S] \nonumber\]

які ми вирішуємо для концентрації комплексу фермент—субстрат

\[[E S]=\frac{[E]_{0}[S]}{\frac{k_{-1}+k_{2}}{k_{1}}+[S]}=\frac{[E]_{0}[S]}{K_{m}+[S]} \label{13.24}\]

де K _m - постійна Міхаеліса. Заміна рівняння\ ref {13.24} на рівняння\ ref {13.21} залишає нам остаточне рівняння швидкості.

\[\frac{d[P]}{d t}=\frac{k_{2}[E]_{0}[S]}{K_{m}+[S]} \label{13.25}\]

Графік Equation\ ref {13.25}, як показано на малюнку Template:index, допомагає нам визначити умови, в яких ми можемо використовувати швидкість ферментативної реакції для кількісного аналізу ферменту або субстрату. Для високих концентрацій субстрату, де [S] >> K _m, Equation\ ref {13.25} спрощує

\[\frac{d[P]}{d t}=\frac{k_{2}[E]_{0}[S]}{K_{m}+[S]} \approx \frac{k_{2}[E]_{0}[S]}{[S]}=k_{2}[E]_{0}=V_{\max } \label{13.26}\]

де V _max - максимальна швидкість для каталізованої реакції. За цих умов реакція є псевдонульовим порядком у субстраті, і ми можемо використовувати V _max для обчислення концентрації ферменту, як правило, за допомогою методу змінного часу. При більш низьких концентраціях субстрату, де [S] << K _м, рівняння\ ref {13.25} стає

\[\frac{d[P]}{d t}=\frac{k_{2}[E]_{0}[S]}{K_{m}+[S]} \approx \frac{k_{2}[E]_{0}[S]}{K_{m}}=\frac{V_{\max }[S]}{K_{m}} \label{13.27}\]

Оскільки реакція в субстраті першого порядку, ми можемо використовувати швидкість реакції для визначення концентрації субстрату за допомогою методу фіксованого часу.

Рисунок Template:index. Графік рівняння\ ref {13.25} показує межі для аналізу субстратів і ферментів в каталізованому ферментами хімічному кінетичному методі аналізу. Крива в області, виділеній червоним кольором, підпорядковується рівнянню\ ref {13.27}, а крива в області, виділеній зеленим кольором, відповідає рівнянню\ ref {13.26}.

Хімічні кінетичні методи були застосовані для кількісного аналізу ряду ферментів і субстратів [Guilbault, GG. Довідник з ферментативних методів аналізу, Марсель Деккер: Нью-Йорк, 1976]. Одним із прикладів є визначення глюкози на основі її окислення ферментом глюкозоксидазою.

\[\text{glucose}(aq) + \text{H}_2\text{O}(g) \xrightarrow{\text{glucose oxidase}} \text{gluconolactone}(aq) + \text{H}_2\text{O}_2(aq) \nonumber\]

за умов, коли рівняння\ ref {13.20} є дійсним. Реакція контролюється шляхом дотримання швидкості зміни концентрації розчиненого О ₂ за допомогою відповідної вольтамметричної методики.

Одним із способів вимірювання концентрації розчиненого O ₂ є амперометричний датчик Кларка, описаний в главі 11.

Неферментно-каталізовані реакції

Метод змінного часу також використовується для визначення концентрації неферментативних каталізаторів. Один із прикладів використовує відновлення H _{2 O 2} тіосульфатом, йодидом або гідрохіноном, реакцією, каталізованою слідовими кількостями обраних іонів металів. Наприклад, зменшення Н ₂ О ₂ на I ^—

\[2 \mathrm{I}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}_{2}(a q)+2 \mathrm{H}_{3} \mathrm{O}^{+}(a q) \longrightarrow 4 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{I}_{2}(a q) \nonumber\]

каталізується Mo (VI), W (VI) і Zr (IV). Аналіз зі змінним часом проводиться шляхом додавання в кожен розчин невеликої фіксованої кількості аскорбінової кислоти. У міру вироблення I ₂ він швидко окислює аскорбінову кислоту і відновлюється назад до I ^—. Як тільки вся аскорбінова кислота буде витрачена, наявність надлишку I ₂ забезпечує візуальну кінцеву точку.

Некаталітичні реакції

Хімічні кінетичні методи не настільки поширені для кількісного аналізу аналітів в некаталітичних реакціях. Оскільки їм не вистачає підвищення швидкості реакції, що дозволяє каталізатор, некаталітичний метод, як правило, не є корисним для визначення малих концентрацій аналіту. Некаталітичні методи для неорганічних аналітів зазвичай базуються на реакції комплексоутворення. Одним із прикладів є визначення алюмінію в сироватці крові шляхом вимірювання початкової швидкості утворення його комплексу з 2-гідрокси-1-нафтальдегідом р -метоксибензоїл-гідразоном [Іоанну. П. С.; Піперакі, Е.А. Клін. Хім. 1986, 32, 1481—1483]. Найбільша кількість некаталітичних методів, однак, призначено для кількісного аналізу органічних аналітів. Наприклад, інсектицид метилпаратіон був визначений шляхом вимірювання його швидкості гідролізу в лужних розчині [Cruces Blanco, C.; Garcia Sanchez, F. Int. Дж. Енвірон. Анальний. Хім. 1990, 38, 513—523].

Характеристика додатків

Хімічні кінетичні методи також знаходять застосування при визначенні констант швидкості і в з'ясуванні механізмів реакції. Два приклади з кінетичного аналізу ферментів ілюструють ці програми.

Визначення V _max і K _m для ферментно-каталізованих реакцій

Значення V _max і K _m для ферментативної реакції становлять значний інтерес при вивченні клітинної хімії. Для ферменту, який слідує механізму в реакції\ ref {13.20}, V _max еквівалентний k 2\(\times\) [E] ₀, де [E] ₀ - концентрація ферменту, а k ₂ - оборот ферменту число. Число обороту ферменту - це максимальна кількість молекул субстрату, перетворених у продукт одним активним сайтом на ферменті, за одиницю часу. Таким чином, число обороту забезпечує пряму вказівку каталітичної ефективності активного сайту. Константа Michaelis, K _m, є значною, оскільки вона забезпечує оцінку внутрішньоклітинної концентрації субстрату [(a) Northup, D.B. J. Chem. Едук. 1998, 75, 1153—1157; (б) Зубай, Г. Біохімія, Macmillan Publishing Co.: Нью-Йорк, 2-е видання, стор 269].

Число обороту ферменту також відомо як k _cat і дорівнює V _max/[E] ₀. Для механізму в реакції\ ref {13.20} k _cat еквівалентно k ₂. Для більш складних механізмів k _cat є функцією додаткових констант швидкості.

Як показано на малюнку Template:index, ми можемо знайти значення для V _max і K _m шляхом вимірювання швидкості реакції для малих і для великих концентрацій субстрату. На жаль, це не завжди практично, оскільки обмежена розчинність субстрату може перешкодити нам використовувати великі концентрації субстрату, необхідні для визначення V _max. Інший підхід полягає в тому, щоб переписати Equation\ ref {13.25}, приймаючи його взаємний

\ [\ розрив {1} {d [P]/d t} =\ гідророзриву {1} {v} =\ гідророзриву {K_ {m}} {V_ {\ max}}\ раз\ гідророзриву {1} {[S]} +\ розрив {1} {V_ {\ max}}\ етикетка {13.28}\]

де v - швидкість реакції. Як показано на малюнку Template:index}, ділянка 1/ v проти 1/ [S], який називається подвійним зворотним або лінією-Берком ділянкою, є прямою лінією з _{нахилом} K м/V _max, a y -перехоплення 1/ V _max, і x -перехоплення —1/ K _м.

Рисунок Template:index. Графік рівняння\ ref {13.25} з використанням рівняння\ ref {ref {13.28}.

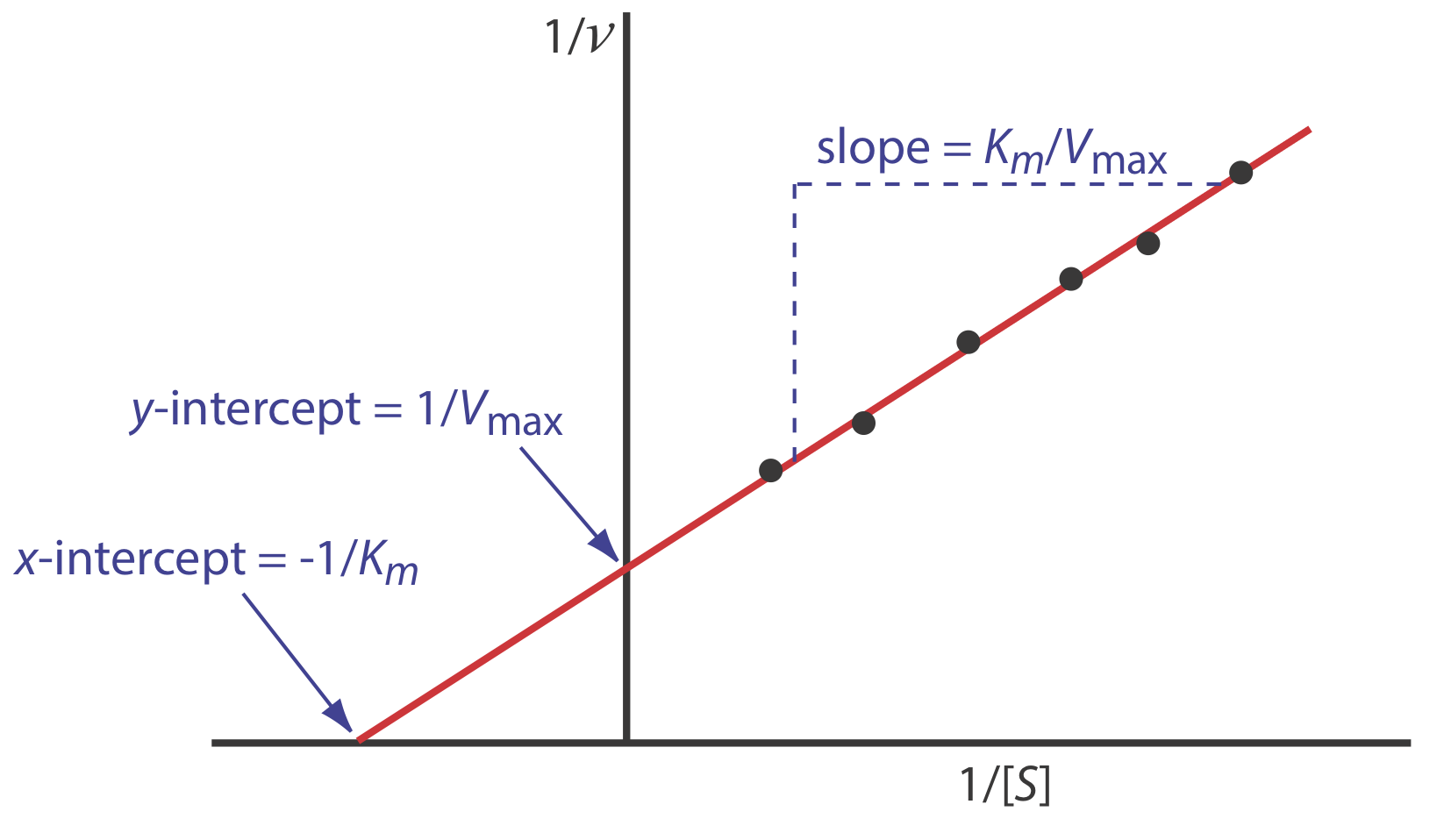
У главі 5 ми зазначили, що при зіткненні з нелінійною моделлю і Equation\ ref {13.25} є одним із прикладів нелінійної моделі, можливо, можна переписати рівняння в лінійній формі. Це стратегія, яка використовується тут. Лінеаризація нелінійної моделі не позбавлена обмежень, два з яких заслуговують на коротку згадку. По-перше, оскільки ми навряд чи матимемо дані для великих концентрацій субстрату, ми не матимемо багато точок даних для малих значень 1/ [S]. Як результат, наше визначення значення y -перехоплення спирається на значну екстраполяцію. По-друге, прийняття зворотної швидкості спотворює експериментальну помилку таким чином, що може знешкодити припущення про лінійну регресію. Нелінійна регресія забезпечує більш строгий метод пристосування Equation\ ref {13.25} до експериментальних даних. Деталі виходять за межі рівня цього підручника, але ви можете проконсультуватися з Massart, D.L.; Вандегінст, Б.Г.; Buydens, Л.М. Де Йонг, С.; Lewi, PJ; Смайер-Вербеке, J. «Нелінійна регресія», який є главою 11 в Довіднику з хемометрики та кваліметрії: Частина А, Elsevier: Амстердам, 1997, для отримання додаткової інформації. Симплексний алгоритм, описаний у главі 14 цього тексту, також може бути використаний для пристосування нелінійного рівняння до експериментальних даних.

Приклад Template:index

Реакція між мононуклеотидом нікотинаміду та АТФ з утворенням нікотинеаміду - аденіндинуклеотиду та пірофосфату каталізується ферментом нікотинамідмононуклеотид аденілілтрансферази [(а) Аткінсон, М.Р.; Джексон, Дж. Ф.; Мортон, Р.К. Дж. 1961, 80, 318—323; (б) Вілкінсон, Г.Н. Біохім. Дж. 1961, 80, 324—332]. У наступній таблиці наведені типові дані, отримані при рН 4,95. Субстратом, S, є мононуклеотид нікотинаміду, а початкова швидкість, v, - мкмоль нікотинаміду - аденіндинуклеотиду, утвореного в 3-хвилинному періоді реакції.

[S] (мМ)	v (мкмоль)	[S] (мМ)	v (мкмоль)
0.138	0,148	0,560	0,324
0,220	0.171	0.766	0,390
0,291	0,234	1.460	0,493

Визначити значення для V _max і K _м.

Рішення

На малюнку Template:index показано графік Linewaver—Burk для цих даних та рівняння регресії результату. Використовуючи y -перехоплення, обчислюємо V _max як

\[V_{\max }=\frac{1}{y\text {-intercept }}=\frac{1}{1.708 \: \mu \mathrm{mol}^{-1}}=0.585 \: \mu \mathrm{mol} \nonumber\]

і за допомогою ухилу знаходимо, що K _m

\[K_{m} = \text {slope} \times V_{\max}=0.7528 \: \mu \mathrm{mol}^{-1} \mathrm{mM} \times 0.585 \: \mu \mathrm{mol}=0.440 \mathrm{ mM} \nonumber\]

Рисунок Template:index. Графік Linewaver—Burk та рівняння регресії для даних у прикладі Template:index.

Вправа Template:index

Наступні дані були зібрані під час окислення катехолу (субстрату) до o -хінону ферментом o -дифенілоксидази. За реакцією слідував моніторинг зміни поглинання на 540 нм. Дані в цій вправі адаптовані з jkimball.

[катехол] (мМ):	0.3	0.6	1.2	4.8
швидкість (\(\Delta\)AU/хв):	0,020	0,035	0,048	0.081

Відповідь

На малюнку нижче показано графік Лінвівера — Берка та рівняння для даних. Y -перехоплення 9,974 хв/ (\(\Delta\)AU еквівалентно 1/ V _max; таким чином, V _max дорівнює 0,10\(\Delta\) AU/хв. Ухил 11,89 хв/ (\ Delta\) Au•мм еквівалентний K _м/ V _max; таким чином, K _m дорівнює 1,2 мм.

Вияснення механізмів інгібування ферментного каталізу

Коли інгібітор взаємодіє з ферментом, він знижує каталітичну ефективність ферменту. Незворотний інгібітор ковалентно зв'язується з активною ділянкою ферменту, виробляючи постійну втрату каталітичної ефективності, навіть якщо ми зменшуємо концентрацію інгібітора. Оборотний інгібітор утворює нековалентний комплекс з ферментом, в результаті чого відбувається тимчасове зниження каталітичної ефективності. Якщо видалити інгібітор, каталітична ефективність ферменту повертається до нормального рівня.

Існує кілька шляхів оборотного зв'язування інгібітора та ферменту, як показано на малюнку Template:index. У конкурентному інгібуванні субстрат і інгібітор конкурують за один і той же активний сайт на ферменті. Оскільки субстрат не може зв'язуватися з комплексом фермент-інгібітор, EI, каталітична ефективність ферменту для субстрату знижується. При неконкурентному інгібуванні субстрат і інгібітор зв'язуються з різними активними ділянками на ферменті, утворюючи фермент—субстрат-інгібітор, або комплекс ESI. Утворення комплексу ESI знижує каталітичну ефективність, оскільки тільки комплекс фермент—субстрат реагує на формування продукту. Нарешті, при неконкурентному інгібуванні інгібітор зв'язується з комплексом фермент—субстрат, утворюючи неактивний комплекс ESI.

Рисунок Template:index. Механізми оборотного інгібування ферментного каталізу. Е: фермент, S: субстрат, P: продукт, I: інгібітор, ES: фермент—субстратний комплекс, EI: фермент—інгібітор com- plex, ESI: фермент—субстрат-інгібіторний комплекс.

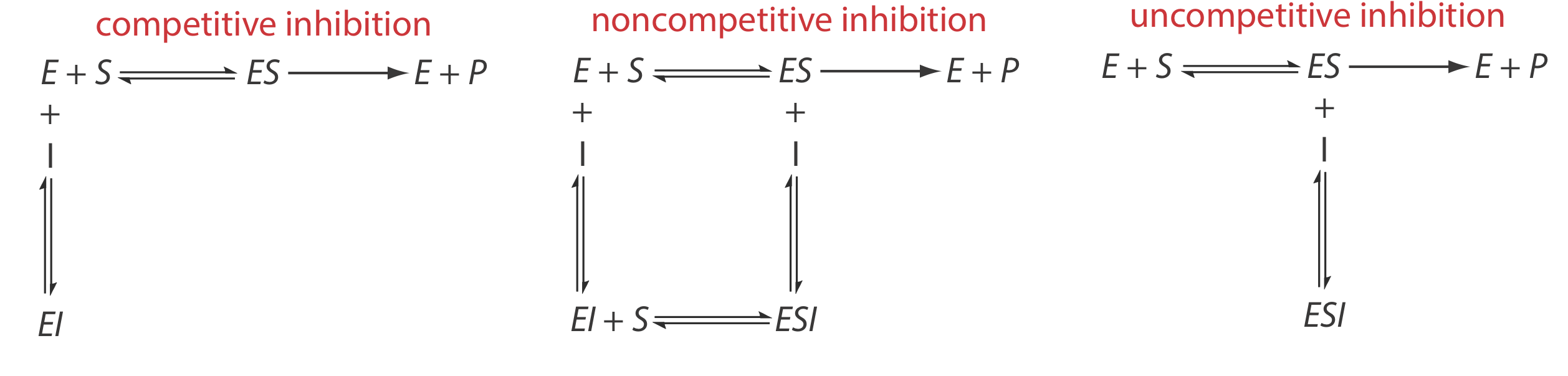
Ми можемо визначити тип оборотного гальмування, спостерігаючи, як зміна концентрації інгібітора впливає на взаємозв'язок між швидкістю реакції та концентрацією субстрату. Як показано на малюнку Template:index, коли ми показуємо кінетичні дані, використовуючи як графік Linewaver-Burk, легко визначити, який механізм діє. Наприклад, збільшення нахилу, зменшення x -перехоплення і відсутність зміни у -перехоплення вказує на конкурентне гальмування. Оскільки зв'язування інгібітора є оборотним, ми все ще можемо отримати ту саму максимальну швидкість - таким чином постійне значення для y -перехоплення - шляхом додавання достатньої кількості субстрату, щоб повністю витіснити інгібітор. Оскільки потрібно більше субстрату, значення K _m збільшується, що пояснює збільшення нахилу та зменшення значення x -перехоплення.

Рисунок Template:index. Linewaver - Burk ділянки для конкурентного гальмування, неконкурентного гальмування та неконкурентного гальмування. Товста синя лінія в кожному сюжеті показує кінетичну поведінку при відсутності інгібітора, а тонкі сині лінії в кожному сюжеті показують зміну поведінки для збільшення концентрації інгібітора. У кожному сюжеті концентрація інгібітора збільшується в напрямку зеленої стрілки.

Приклад Template:index

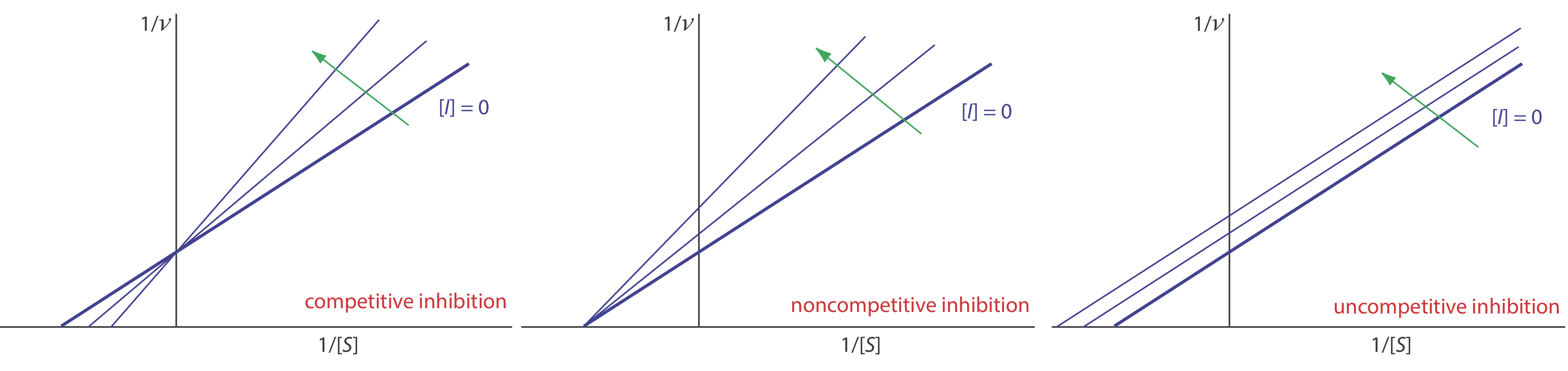
Вправа Template:index надає кінетичні дані для окислення катехолу (субстрату) до o -хінону ферментом o -дифенілоксидази за відсутності інгібітора. Наступні додаткові дані доступні при проведенні реакції в присутності р -гідроксибензойної кислоти, PBHA. Чи є PBHA інгібітором цієї реакції, і якщо так, то який тип інгібітора це? Дані в цій вправі адаптовані з jkimball.

[катехол] (мМ):	0.3	0.6	1.2	4.8
швидкість (\(\Delta\)AU/хв):	0.011	0.019	0,022	0,060

Рішення

Рисунок Template:index показує результуючий графік Linewaver—Burk для даних у Вправі Template:index і Приклад Template:index. Хоча два y -перехоплення не однакові за значенням - результат невизначеності у вимірюванні ставок - сюжет говорить про те, що PBHA є конкурентним інгібітором реакції ферменту з катехолом.

Рисунок Template:index. Linewaver — Берк будує графіки для даних у Вправі Template:index і Приклад Template:index.

Вправа Template:index

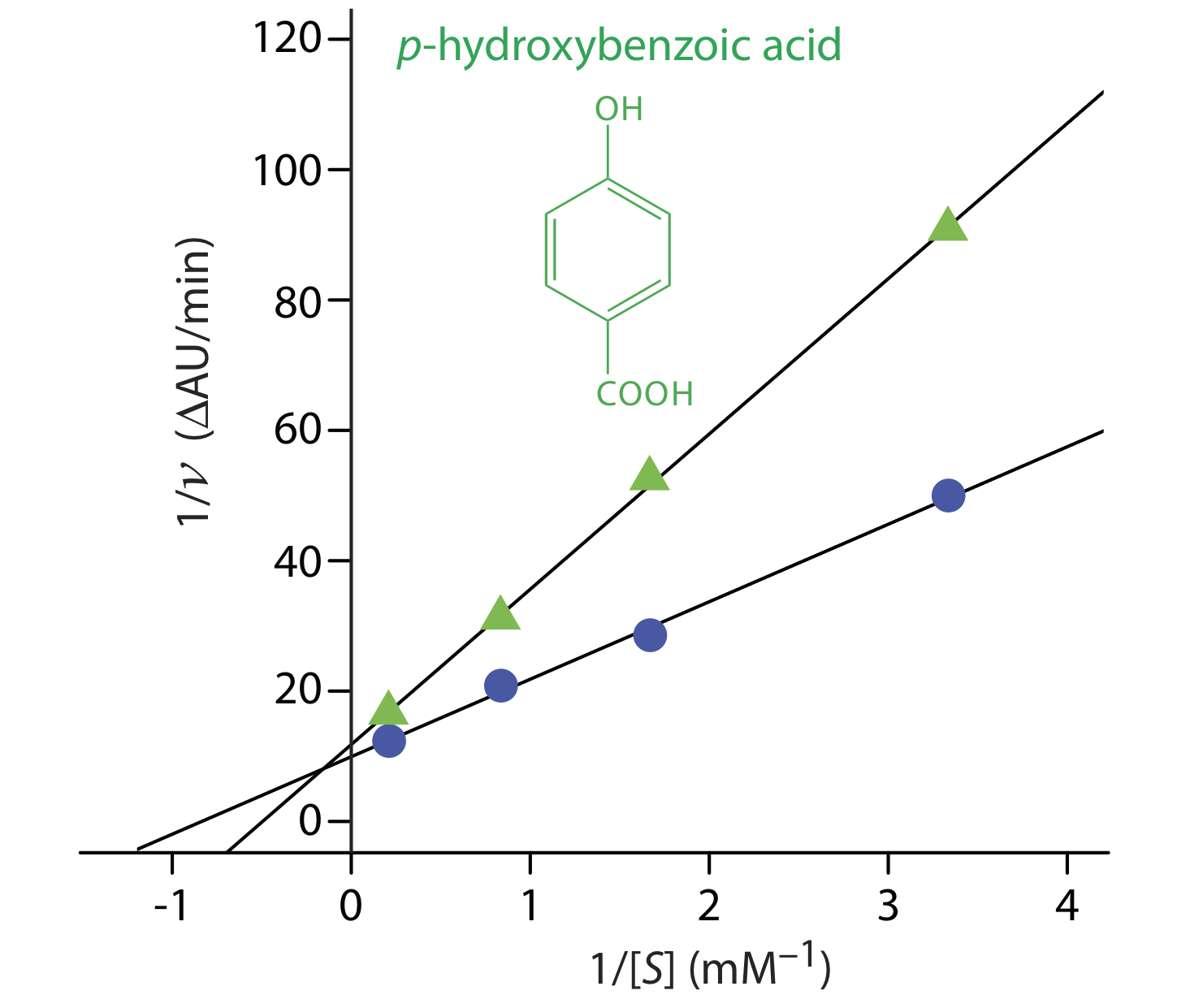
Вправа Template:index надає кінетичні дані для окислення катехолу (субстрату) до o -хінону ферментом o -дифенілоксидази за відсутності інгібітора. Наступні додаткові дані доступні при проведенні реакції в присутності фенілтіосечовини. Чи є фенілтіосечовина інгібітором цієї реакції, і якщо так, то який тип інгібітора це? Дані в цій вправі адаптовані з jkimball.

[катехол] (мМ):	0.3	0.6	1.2	4.8
швидкість (\(\Delta\)AU/хв):	0,010	0,016	0,024	0,040

Відповідь

На малюнку нижче показані графіки Linewaver — Burk для двох наборів даних. Майже ідентичні х -перехоплення говорять про те, що фенілтіосечовина є неконкурентним інгібітором.

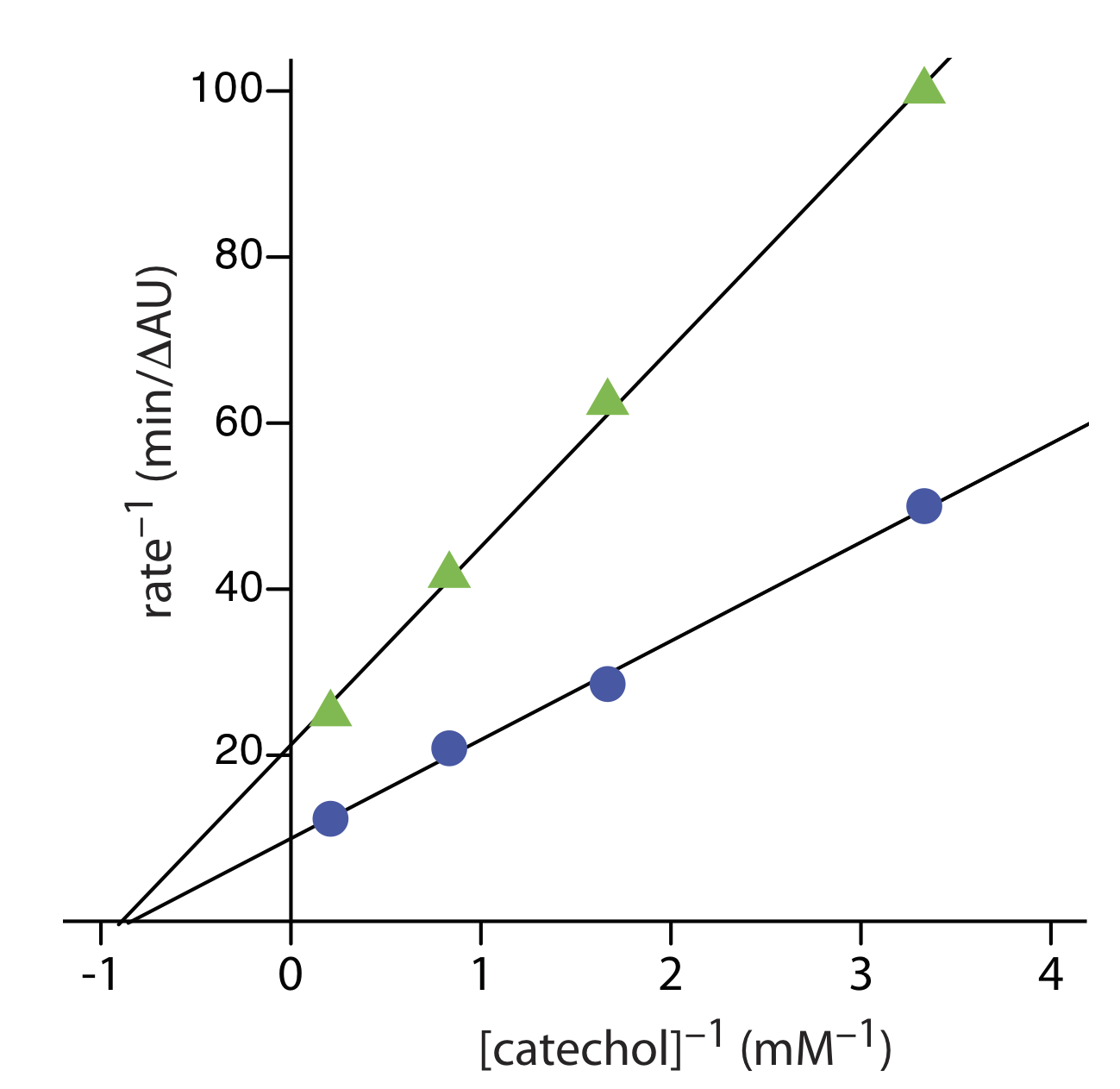
Оцінка хімічних кінетичних методів

Масштаб операції

Межа виявлення для хімічного кінетичного методу коливається від незначних компонентів до ультратрасових компонентів і визначається двома факторами: швидкістю реакції та інструментальною технікою, яка використовується для контролю швидкості. Оскільки сигнал прямо пропорційний швидкості реакції, швидша реакція, як правило, призводить до нижньої межі виявлення. При інших рівних факторах межі виявлення менші для каталітичних реакцій, ніж для некаталітичних реакцій. Не дивно, що деякі з найбільш ранніх хімічних кінетичних методів скористалися каталітичними реакціями. Наприклад, ультраслідові рівні Cu (<1 ppb) визначають шляхом вимірювання його каталітичного впливу на окислювально-відновну реакцію між гідрохіноном і H ₂ O ₂.

При відсутності каталізатора більшість хімічних кінетичних методів для органічних сполук використовують реакції з відносно повільними швидкостями, що обмежує аналіз незначними і більш високими концентраціями слідових аналітів. Некаталітичні хімічні кінетичні методи для неорганічних сполук, які використовують реакції комплексоутворення метал-ліганд, можуть бути швидкими або повільними, з межами виявлення варіюються від сліду до незначного аналіту.

Другим фактором, який впливає на межу виявлення методу, є прилади, що використовуються для контролю прогресу реакції. Більшість реакцій контролюються спектрофотометрично або електрохімічно. Масштаби роботи для цих методів розглядаються в главі 10 та главі 11.

Точність

Як зазначалося раніше, хімічний кінетичний метод потенційно піддається більшим похибкам, ніж метод рівноваги через вплив неконтрольованих або погано контрольованих змінних, таких як температура або рН. Хоча хімічний кінетичний метод прямого обчислення може досягти помірно точних результатів (відносна похибка 1— 5%), точність часто набагато гірша. Методи підгонки кривої забезпечують значне поліпшення точності, оскільки вони використовують більше даних. Наприклад, в одному дослідженні точність була покращена на два порядку величини - від помилок 500% до 5% - шляхом заміни аналізу прямого обчислення аналізом кривої [Pauch, J.B.; Margerum, D.W. Anal. Хім. 1969, 41, 226—232]. Хоча це не обговорюється в цьому розділі, методи аналізу даних, які включають здатність компенсувати експериментальні помилки, можуть призвести до значного поліпшення точності [(a) Holler, FJ; Calhoun, R.K.; McLanahan, SF Anal. Хім. 1982, 54, 755—761; (б) Вентцель, П.Д.; Крауч, С.Р. анал. Хім. 1986, 58, 2851—2855; (c) Вентцель, П.Д.; Крауч, С.Р. анал. Хім. 1986, 58, 2855—2858].

Точність

Точність хімічного кінетичного методу обмежена співвідношенням сигнал/шум приладу, що використовується для моніторингу прогресу реакції. При використанні інтегрального методу зазвичай можлива точність 1— 2%. Точність для диференціального методу може бути дещо біднішою, особливо якщо сигнал шумний.

Чутливість

Ми можемо покращити чутливість одноточкового інтегрального методу з фіксованим часом, зробивши вимірювання в умовах, коли концентрація контрольованих видів максимально велика. Під час моніторингу концентрації аналіту - або концентрації будь-якого іншого реагенту - ми хочемо провести вимірювання на початку реакції, перш ніж його концентрація зменшиться. З іншого боку, якщо ми вирішили контролювати один з продуктів реакції, то краще проводити вимірювання в більш тривалий час. Для двоточкового методу інтеграла з фіксованим часом ми можемо покращити чутливість, збільшивши різницю між кратами t ₁ і t ₂. Як обговорювалося раніше, чутливість методу швидкості покращується, коли ми вирішуємо виміряти початкову норму.

Вибірковість

Аналіз близькоспоріднених сполук, про що йшлося в попередніх розділах, часто ускладнюється їх схильністю заважати один одному. Щоб подолати цю проблему, нам зазвичай потрібно відокремити аналіт та інтерферент перед завершенням аналізу. Однією з переваг хімічного кінетичного методу є те, що часто можна регулювати умови реакції так, щоб аналіт і інтерферент мали різну швидкість реакції. Якщо різниця у відповідних швидкостях досить велика, то один вид повністю відреагує до того, як інший вид матиме шанс відреагувати.

Необхідність аналізу декількох аналітів у складних сумішах, звичайно, є однією з переваг методів поділу, висвітлених у главі 12. Кінетичні методики забезпечують альтернативний підхід для простих сумішей.

Ми можемо використовувати відповідні інтегровані закони швидкості, щоб знайти умови, необхідні для відокремлення швидше реагуючих видів від більш повільно реагуючих видів. Розглянемо систему, яка складається з аналіту, А та інтерферента, В, обидві з яких показують кінетику першого порядку із загальним реагентом. Щоб уникнути перешкод, відносні величини їх констант швидкості повинні бути досить різними. Дроби, f, A і B, які залишаються в будь-який момент часу, t, визначаються наступними рівняннями

\[\left(f_{A}\right)_{t}=\frac{[A]_{t}}{[A]_{0}} \label{13.29}\]

\[\left(f_{B}\right)_{t}=\frac{[B]_{t}}{[B]_{0}} \label{13.30}\]

де [A] ₀ і [B] ₀ - початкові концентрації A і B відповідно. Перевпорядкування рівняння\ ref {13.2} і заміна в Рівняння\ ref {13.29} або Equation\ ref {13.30} залишає використання з наступними двома рівняннями.

\[\ln \frac{[A]_{t}}{[A]_{0}}=\ln \left(f_{A}\right)_{t}=-k_{A} t \label{13.31}\]

\[\ln \frac{[B]_{t}}{[B]_{0}}=\ln \left(f_{B}\right)_{t}=-k_{B} t \label{13.32}\]

де k _A і k _B - константи швидкості для A і для B. Рівняння ділення\ ref {13.31} за рівнянням\ ref {13.32} залиште нам

\[\frac{k_{A}}{k_{B}}=\frac{\ln \left(f_{\mathcal{A}}\right)_{t}}{\ln \left(f_{B}\right)_{t}} \nonumber\]

Припустимо, ми хочемо, щоб 99% A реагували до того, як 1% B реагує. Частка А, яка залишається, становить 0,01, а частка B, яка залишається, становить 0,99, що вимагає, щоб

\[\frac{k_{A}}{k_{B}}=\frac{\ln \left(f_{A}\right)_{t}}{\ln \left(f_{B}\right)_{t}}=\frac{\ln (0.01)}{\ln (0.99)}=460 \nonumber\]

константа швидкості для А повинна бути не менше ніж в 460 разів більше, ніж для B. Коли ця умова виконується, ми можемо визначити концентрацію аналіта до того, як інтерферент почне реагувати. Якщо аналіт має більш повільну реакцію, то ми можемо визначити його концентрацію після того, як дозволимо інтерференту реагувати на завершення.

Цей метод регулювання швидкості реакції корисний, якщо нам потрібно проаналізувати аналіт у присутності інтерференту, але недоцільний, якщо і A, і B є аналітами, оскільки умова, яка сприяє аналізу А, не сприятиме аналізу B. Наприклад, якщо відрегулювати умови так, щоб 99% А реагували за 5 с, то 99% B повинні реагувати протягом 0,01 с, якщо він має більш швидку кінетику, або в 2300 с, якщо він має більш повільну кінетику. Реакція В занадто швидка або занадто повільна, щоб зробити це корисним аналітичним методом.

Що робити, якщо різниця в константах швидкості для A і B істотно не відрізняється? Ми все ще можемо завершити аналіз, якщо можемо одночасно контролювати обидва види. Оскільки і А, і В реагують одночасно, інтегрована форма закону про ставку першого порядку стає

\[C_{t}=[A]_{t}+[B]_{t}=[A]_{0} e^{-k_{A}t}+[B]_{0} e^{-k_{B}t} \label{13.33}\]

де C _t - сумарна концентрація А і В за часом, т. Якщо виміряти C _t в рази t ₁ і t ₂, ми можемо вирішити отриману пару одночасних рівнянь для визначення значень [A] ₀ і [B] ₀. Константи швидкості k _A і k _B визначаються в окремих експериментах з використанням стандартних розв'язків A і B.

Рівняння\ ref {13.33} також може служити основою для методу кривої підгонки. Як показано на малюнку Template:index, ділянка ln (C _t) як функція часу складається з двох областей. У коротші терміни графік викривлений, оскільки A і B реагують одночасно. Однак у більш пізні часи концентрація швидшого реагуючого компонента, A, зменшується до нуля, а Equation\ ref {13.33} спрощує

\[C_{t} \approx[B]_{t}=[B]_{0} e^{-k_{B}t} \nonumber\]

У цих умовах графік ln (C _t) проти часу є лінійним. Екстраполяція лінійної частини до t = 0 дає [B] ₀, причому [A] ₀ визначається різницею.

Рисунок Template:index. Кінетичне визначення повільніше реагуючого аналіту, В, в присутності більш швидкого реагуючого аналіту, А. Константи швидкості для двох аналітів: k _A = 1 min ^—1 і k _B = 0,1 хв ^—1.

Приклад Template:index

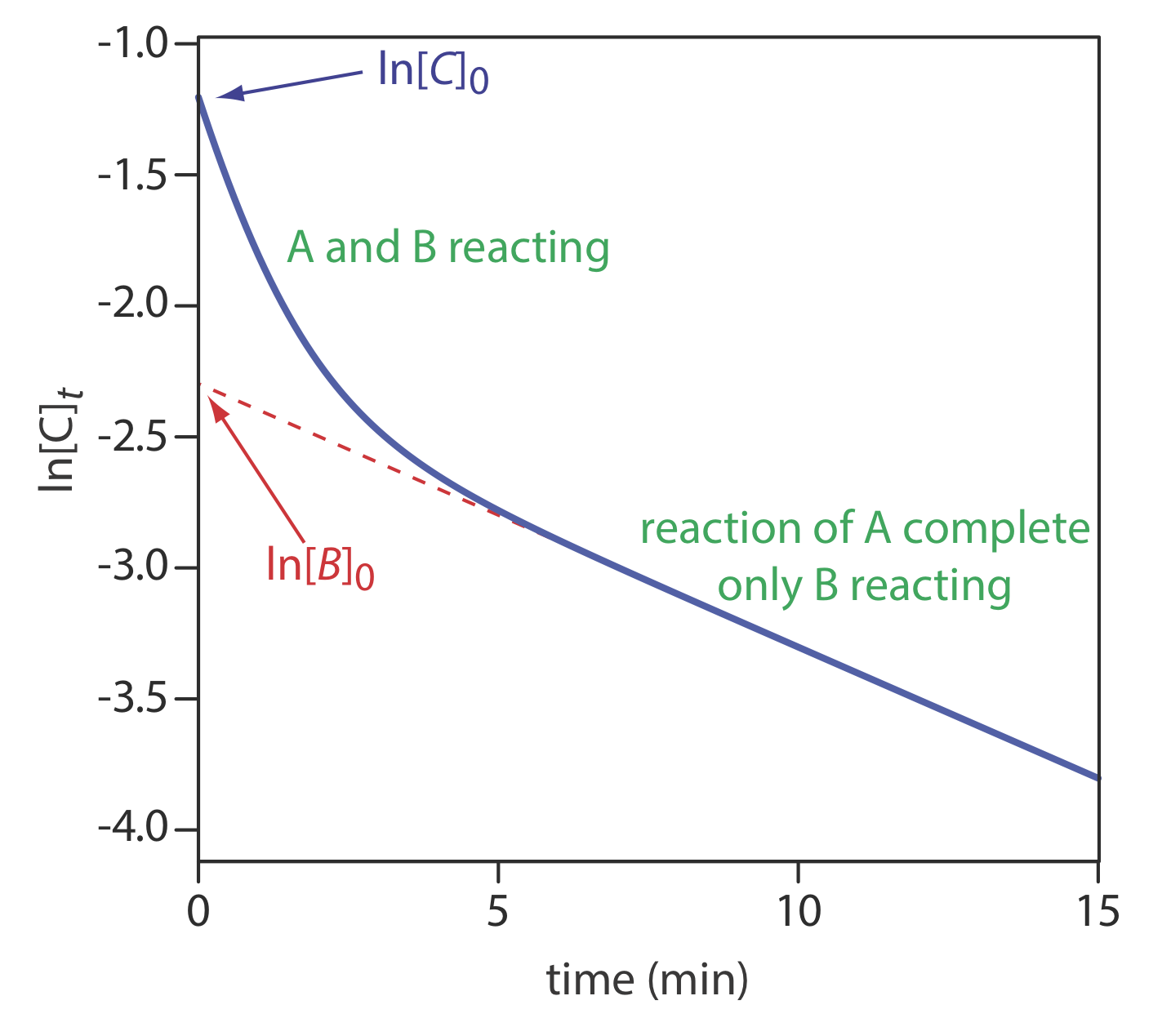
Використовуйте дані на рисунку Template:index для визначення концентрацій A та B у вихідному зразку.

Рішення

Екстраполяція лінійної частини кривої назад до t = 0 дає ln [B] ₀ як —2.3, або a [B] ₀ з 0,10 М. При t = 0, ln [C] ₀ дорівнює —1.2, що відповідає a [C] ₀ або 0.30 М. Тому що [C] ₀ = [A] ₀ + [B] ₀, концентрація А в вихідному зразку становить 0,20 М.

Час, вартість та обладнання

Автоматизований хіміко-кінетичний метод аналізу забезпечує швидкий засіб для аналізу зразків, пропускна здатність яких коливається від декількох сотень до декількох тисяч визначень на годину. Початкові витрати на запуск можуть бути досить високими, оскільки для автоматизованого аналізу потрібен спеціальний інструмент, призначений для задоволення конкретних потреб аналізу. Коли вимірювання обробляються вручну, хімічний кінетичний метод вимагає рутинно доступного обладнання та приладів, хоча пропускна здатність зразка набагато нижча, ніж при автоматизованому методі.