5.7: Проблеми

Last updated
Save as PDF

Page ID: 24959

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

1. Припустимо, ви використовуєте серійне розведення для приготування 100 мл кожного з серії стандартів з концентраціями\(1.00 \times10^{-5}\),\(1.00 \times10^{-4}\),\(1.00 \times10^{-3}\),, і\(1.00 \times10^{-2}\) M з 0.100 M вихідного розчину. Обчисліть невизначеність для кожного рішення, використовуючи поширення невизначеності, і порівняйте з невизначеністю, якщо ви готуєте кожне рішення як єдине розведення вихідного розчину. Допуски для різних видів об'ємного скляного посуду і цифрових піпетів ви знайдете в таблиці 4.2.1 і таблиці 4.2.2. Припустимо, що невизначеність у молярності вихідного розчину становить ± 0,0002.

2. Три повторювані визначення _{загальної} суми S для стандартного рішення, яке становить 10,0 проміле в аналіті, дають значення 0,163, 0,157 та 0,161 (довільні одиниці). Сигнал для заготовки реагенту - 0,002. Обчисліть концентрацію аналіту в пробі з сигналом 0,118.

3. 10,00-г проба, що містить аналіт, переносять в об'ємну колбу об'ємом об'ємом об'ємом об'ємом об'ємом 250 мл і розводять до об'єму. При розведенні 10,00 мл аліквота отриманого розчину до 25,00 мл він подає сигнал 0,235 (довільні одиниці). Другу 10,00-мл порцію розчину заливають 10,00 мл стандартного розчину аналіту 1.00-ppm і розводять до 25,00 мл. Сигнал для шипоподібного зразка - 0,502. Обчисліть ваговий відсоток аналіту в вихідному зразку.

4. Зразок 50,00 мл, який містить аналіт, дає сигнал 11,5 (довільні одиниці). Друга 50 мл аліквота зразка, яка шипується 1,00 мл стандартного розчину аналіту 10,0 ppm, дає сигнал 23,1. Яка концентрація аналіту в вихідному зразку?

5. Стандартна доповнення калібрувальної кривої на основі Рівняння 5.3.10 розміщує\(S_{spike} \times (V_o + V_{std})\) на осі y і\(C_{std} \times V_{std}\) на осі x. Виведіть рівняння для нахилу та y -перехоплення та поясніть, як можна визначити кількість аналіту у зразку за калібрувальною кривою. Крім того, чітко поясніть, чому ви не можете _{побудувати шип} S на осі y та\(C_{std} \times \{V_{std}/(V_o + V_{std})\}\) на осі x.

6. Стандартний зразок містить 10,0 мг/л аналіту і 15,0 мг/л внутрішнього стандарту. Аналіз вибірки дає сигнали для аналіта і внутрішнього стандарту 0,155 і 0,233 (довільні одиниці) відповідно. До зразка додають достатній внутрішній стандарт, щоб зробити його концентрацію 15,0 мг/л, аналіз зразка дає сигнали для аналіту і внутрішнього стандарту 0,274 і 0,198 відповідно. Повідомте про концентрацію аналіта в зразку.

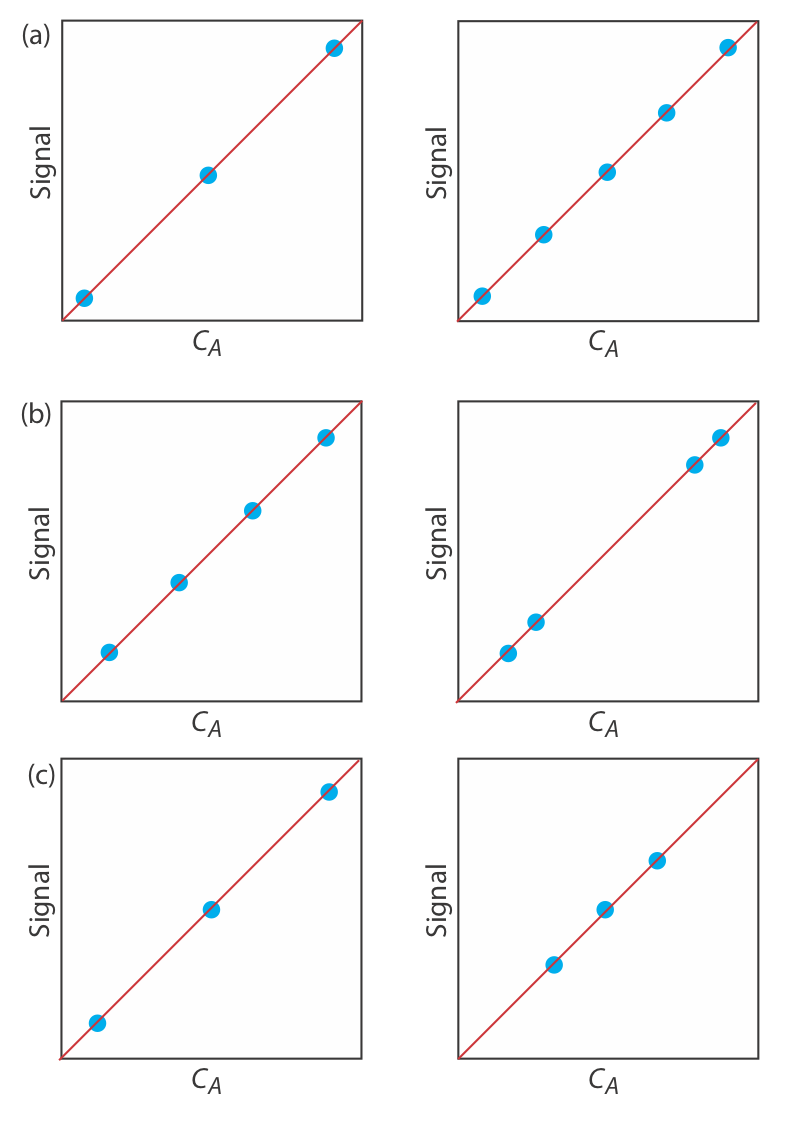
7. Для кожної пари калібрувальних кривих, показаних нижче, виберіть калібрувальну криву, яка використовує більш відповідний набір стандартів. Коротко поясніть причини вашого вибору. Шкали для осі x та осі y однакові для кожної пари.

8. Наступні дані призначені для серії зовнішніх стандартів Cd ² ⁺ буферизованих до рН 4,6.

[Кд ²⁺] (Нм)	15.4	30.4	44.9	59,0	72.7	86.0
\(S_{spike}\)(нА)	4.8	11.4	18.2	26.6	32.3	37.7

(a) Використовуйте лінійний регресійний аналіз, щоб визначити рівняння для калібрувальної кривої та повідомити довірчі інтервали для нахилу та перехоплення y.

(б) Побудувати сюжет залишків і прокоментувати їх значення.

При рН 3,7 були записані наступні дані для того ж набору зовнішніх стандартів.

[Кд ²⁺] (Нм)	15.4	30.4	44.9	59,0	72.7	86.0
\(S_{spike}\)(нА)	15,0	42.7	58.5	77.0	101	118

(d) Один зразок буферується до рН 3,7 і аналізується на кадмій, даючи сигнал 66,3 нА. Повідомте про концентрацію Cd ² ⁺ у зразку та його 95% довірчий інтервал.

Дані в цій проблемі взяті з Войцеховського, М.; Бальцерзака, J. Anal. Чим. Акт 1991, 249, 433—445.

9. Для визначення концентрації аналіту в пробі проводиться стандартне додавання. Аналізують порцію зразка 5,00 мл, а потім додають послідовні 0,10-мл шипи стандарту 600,0 ppb аналіту, аналізуючи після кожного спайка. У наступній таблиці наведені результати цього аналізу.

\(V_{spike}\)(мл)	0.00	0,10	0,20	0,30
\(S_{total}\)(довільні одиниці)	15,0	42.7	58.5	77.0

Побудувати відповідну стандартну криву калібрування доповнень і використовувати лінійний регресійний аналіз для визначення концентрації аналіту в вихідному зразку і його 95% довірчого інтервалу.

10. Трост і Олавесн досліджували застосування внутрішньої стандартизації до кількісного аналізу поліядерних ароматичних вуглеводнів. Наступні результати були отримані для аналізу фенантрину з використанням ізотопічно маркованого фенантрину як внутрішнього стандарту. Кожне рішення аналізувалося двічі.

\(C_A/C_{IS}\)

0,50

1,25

2.00

3.00

4.00

\(S_A/S_{IS}\)

0.514

0.522

0,993

1.024

1.486

1.471

2.044

2.080

2.342

2.550

(а) Визначте рівняння для калібрувальної кривої за допомогою лінійної регресії та повідомте довірчі інтервали для нахилу та перехоплення y. Середнє значення сигналів реплікації для кожного стандарту, перш ніж завершити аналіз лінійної регресії.

(б) На підставі ваших результатів поясніть, чому автори прийшли до висновку, що внутрішня стандартизація є недоречною.

Дані в цій задачі взяті від Troost, J.R.; Olavesen, Е. Хім. 1996, 68, 708—711.

11. У розділі 4.6. ми використовували парний t -тест для порівняння двох аналітичних методів, які використовувалися для самостійного аналізу ряду зразків змінного складу. Альтернативним підходом є побудова результатів для одного методу порівняно з результатами для іншого методу. Якщо два методи дають однакові результати, то графік повинен мати очікуваний нахил\(\beta_1\), 1,00 та очікуваний y -перехоплення\(\beta_0\), 0.0. Ми можемо використовувати t -тест для порівняння нахилу і y -перехоплення від лінійної регресії до очікуваних значень. Відповідну статистику тесту для y -перехоплення знайдено шляхом перестановки рівняння 5.4.10.

\[t_{exp} = \frac {|\beta_0 - b_0|} {s_{b_0}} = \frac {|b_0|} {s_{b_0}} \nonumber\]

Перестановка рівняння 5.4.9 дає статистику тесту для нахилу.

\[t_{exp} = \frac {|\beta_1 - b_1} {s_{b_1}} = \frac {|b_1|} {s_{b_1}} \nonumber\]

Переоцініть дані в задачі 25 з глави 4, використовуючи той самий рівень значущості, що і в початковій задачі.

Хоча це загальний підхід для порівняння двох аналітичних методів, він порушує одну з вимог до незваженої лінійної регресії - що невизначені помилки впливають лише на y. Оскільки невизначені помилки впливають на обидва аналітичні методи, результат незваженої лінійної регресії є упередженим. Більш конкретно, регресія занижує нахил, b ₁, і завищує y -перехоплення, b ₀. Ми можемо мінімізувати ефект цього зміщення, розмістивши більш точний аналітичний метод на осі x, використовуючи більше зразків для збільшення ступенів свободи та використовуючи зразки, які рівномірно охоплюють діапазон концентрацій.

Для отримання додаткової інформації див. Miller, J.C.; Міллер, J.N. Статистика аналітичної хімії, 3-е видання. Елліс Хорвуд PTR Прентіс-Холл: Нью-Йорк, 1993. Альтернативні підходи зустрічаються в Hartman, C.; Smeyers-Verbeke, J.; Penninckx, W.; Massart, D.L. Чим. Акта 1997, 338, 19—40, і Цванцигер, HW; SaRBu, C. Анальний. Хім. 1998, 70, 1277—1280.

12. Розглянемо наступні три набори даних, кожен з яких дає значення y для однакових значень x.

х	на ₁	на ₂	на ₃
10.00	8.04	9.14	7.46
8.00	6.95	8.14	6.77
13.00	7.58	8.74	12.74
9.00	8.81	8.77	7.11
11.00	8.33	9.26	7.81
14.00	9.96	8.10	8.84
6.00	7.24	6.13	6.08
4.00	4.26	3.10	5.39
12.00	10.84	9.13	8.15
7.00	4.82	7.26	6.42
5.00	5.68	4.74	5.73

(a) Незважений лінійний регресійний аналіз для трьох наборів даних дає майже однакові результати. До трьох значущих цифр кожен набір даних має нахил 0.500 і y -перехоплення 3.00. Стандартні відхилення в ухилі і y -перехоплення складають 0,118 і 1,125 для кожного набору даних. Всі три стандартних відхилення щодо регресії - 1,24. На основі цих результатів для лінійного регресійного аналізу прокоментуйте подібність наборів даних.

(b) Виконайте лінійний регресійний аналіз для кожного набору даних та переконайтеся, що результати з частини (а) є правильними. Побудувати залишковий графік для кожного набору даних. Чи змінюють ці сюжети ваш висновок з частини (а)? Поясніть.

(d) Набір даних 3, схоже, містить викиди. Видаліть видимий викид і повторно проаналізуйте дані за допомогою лінійної регресії. Прокоментуйте свій результат.

(e) Коротко прокоментуйте важливість візуального вивчення ваших даних.

Ці три набори даних взяті з Anscombe, FJ «Графіки в статистичному аналізі», Амер. Статіс. 1973, 27, 17-21.

13. Фанке та колеги оцінювали метод стандартних доповнень для вольтамметричного визначення Tl. Короткий зміст їх результатів наведено в таблиці нижче.

ppm До додано	Реакція приладу (\(\mu\)A)
0.000	2.53	2.50	2.70	2.63	2.70	2.80	2.52
0,387	8.42	7.96	8.54	8.18	7.70	8.34	7.98
1,851	29.65	28.70	29.05	28.30	29.20	29.95	28.95
5.734	84,8	85.6	86.0	85.2	84.2	86.4	87.8

Використовуйте зважену лінійну регресію для визначення співвідношення стандартизації для цих даних.

Дані в цій проблемі взяті від Франке, J.P.; де Zeeuw, R.A.; Hakkert, R.Anal. Хім. 1978, 50, 1374—1380.