6.3: Використання звичайного розподілу

Затінена область на наступному графіку вказує область зліва від\(x\). Ця область представлена ймовірністю\(P(X < x)\). Звичайні таблиці, комп'ютери та калькулятори забезпечують або обчислюють ймовірність\(P(X < x)\).

Малюнок\(\PageIndex{1}\).

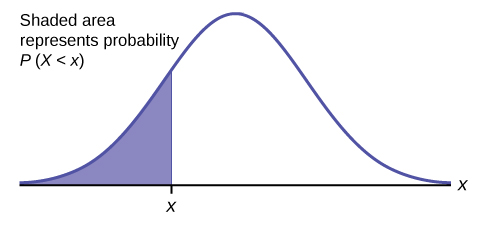
Потім область праворуч\(P(X > x) = 1 – P(X < x)\). Пам'ятайте,\(P(X < x) =\) область зліва від вертикальної лінії наскрізь\(x\). \(P(X > x) = 1 – P(X < x) =\)Область праворуч від вертикальної лінії наскрізь\(x\). \(P(X < x)\)такий же, як\(P(X \leq x)\) і\(P(X > x)\) такий же, як і\(P(X \geq x)\) для безперервних дистрибутивів.

Розрахунки ймовірностей

Імовірності розраховуються за допомогою технології. Існують інструкції, наведені в міру необхідності для калькуляторів TI-83+ і TI-84. Для розрахунку ймовірності скористайтеся таблицями ймовірностей, наведеними в [link] без використання технології. Таблиці містять інструкції щодо їх використання.

Приклад\(\PageIndex{1}\)

Якщо область зліва дорівнює 0,0228, то область праворуч -\(1 - 0.0228 = 0.9772\).

Вправа\(\PageIndex{1}\)

Якщо область зліва від\(x\) є\(0.012\), то яка область праворуч?

Відповідь

\(1 - 0.012 = 0.988\)

Приклад\(\PageIndex{2}\)

Підсумкові бали іспиту в класі статистики зазвичай розподілялися із середнім значенням 63 та стандартним відхиленням п'яти.

1. Знайдіть ймовірність того, що випадково обраний студент набрав більше 65 на іспиті.
2. Знайдіть ймовірність того, що випадково обраний студент набрав менше 85.
3. Знайдіть ^90-й процентиль (тобто знайдіть рахунок,\(k\) який має 90% балів нижче k і 10% балів вище\(k\)).
4. Знайдіть ^70-й процентиль (тобто знайдіть\(k\) такий бал, щоб 70% балів були нижче,\(k\) а 30% балів вище\(k\)).

Відповідь

а. нехай\(X\) = бал на підсумковому іспиті. \(X \sim N(63, 5)\), де\(\mu = 63\) і\(\sigma = 5\)

Намалюйте графік.

Потім знайдіть\(P(x > 65)\).

\[P(x > 65) = 0.3446\nonumber \]

Малюнок\(\PageIndex{2}\).

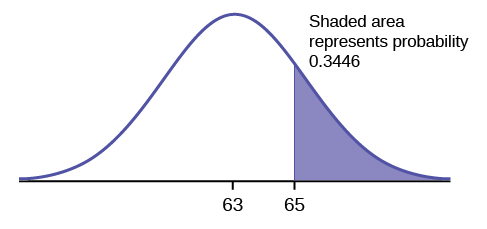
Імовірність того, що будь-який студент, обраний випадковим чином балів більше 65, дорівнює 0,3446.

ВИКОРИСТАННЯ КАЛЬКУЛЯТОРА TI-83, 83+, 84, 84+

Заходимо в 2-й район.

Після натискання 2-го DISTR натисніть 2: normalcdf.

Синтаксис інструкцій такий:

normalcdf (нижнє значення, верхнє значення, середнє, стандартне відхилення) Для цієї задачі: normalcdf (65,1E99,63,5) = 0,3446. Ви отримуєте 1E99 (= 10 ⁹⁹), натиснувши 1, клавішу EE (2-а клавіша), а потім 99. Або замість цього ви можете ввести 10^ 99. Число 10 ⁹⁹ - вихід в правий хвіст нормальної кривої. Ми обчислюємо площу між 65 і 10 ⁹⁹. У деяких випадках нижня кількість області може бути —1E99 (= —10 ⁹⁹). Число —10 ⁹⁹ є виходом у лівому хвості нормальної кривої.

Історична записка

Програма ймовірності TI обчислює\(z\) -score, а потім ймовірність з\(z\) -score. Перед технологією\(z\) -score шукали в стандартній нормальній таблиці ймовірностей (тому що математика занадто громіздка), щоб знайти ймовірність. У цьому прикладі була використана стандартна звичайна таблиця з областю зліва від\(z\) -score. Ви обчислюєте\(z\) -score і шукайте область зліва. Імовірність - область праворуч.

\[z = 65 – 63565 – 635 = 0.4\nonumber \]

Площа зліва 0.6554.

\[P(x > 65) = P(z > 0.4) = 1 – 0.6554 = 0.3446\nonumber \]

ВИКОРИСТАННЯ КАЛЬКУЛЯТОРА TI-83, 83+, 84, 84+

Знайдіть процентиль для студента, який набрав 65 балів:

* Натисніть 2nd Distr
* Натисніть 2:
normalcdf (* Введіть нижню межу, верхню межу, середнє, стандартне відхилення за ним)
* Натисніть ENTER.
Для цього прикладу, кроки
2-й Distr
2: normalcdf (65,12nd EE,99,63,5) ENTER

Імовірність того, що обраний студент набрав більше 65, становить 0.3446.
Щоб знайти ймовірність того, що обраний учень набрав більше 65, відніміть процентиль з 1.

Відповідь

б. намалюйте графік.

Потім\(P(x < 85)\) знайдіть і затіньте графік.

Використовуючи комп'ютер або калькулятор, знайдіть\(P(x < 85) = 1\).

\(\text{normalcdf}(0,85,63,5) = 1\)(раундів до одного)

Імовірність того, що один студент набере менше 85, приблизно одна (або 100%).

Відповідь

с. знайти ^90-й процентиль. Для кожної задачі або частини задачі намалюйте новий графік. Намалюйте\(x\) вісь -. Затіньте область, яка відповідає ^90-му процентилю.

Нехай\(k =\) ^90-й процентиль. Змінна\(k\) розташована на\(x\) -осі. \(P(x < k)\)це область зліва від\(k\). ^90-й\(k\) процентиль розділяє бали іспиту на ті, які однакові або нижче, ніж\(k\) і ті, які однакові або вище. Дев'яносто відсотків тестових балів однакові або нижчі\(k\), а десять відсотків однакові або вище. Змінну часто\(k\) називають критичним значенням.

\(k = 69.4\)

Малюнок\(\PageIndex{3}\).

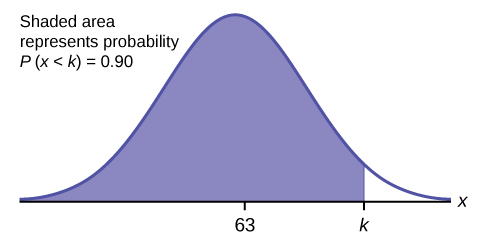
^90-й процентиль дорівнює 69,4. Це означає, що 90% тестових балів падають на рівні 69,4 або нижче, а 10% падають на рівні або вище. Щоб отримати цю відповідь на калькуляторі, виконайте такий крок:

ІнВНорм у 2-му р-н. вНормі (площа ліворуч, середнє, стандартне відхилення)

Для цієї проблеми,\(\text{invNorm}(0.90,63,5) = 69.4\)

Відповідь

d. знайти ^70-й процентиль.

Намалюйте новий графік і позначте його відповідним чином. \(k = 65.6\)

^70-й процентиль дорівнює 65,6. Це означає, що 70% тестових балів падають на рівні 65,6 або нижче, а 30% падають на рівні або вище.

\(\text{invNorm}(0.70,63,5) = 65.6\)

Вправа\(\PageIndex{2}\)

Гольф бали для шкільної команди були зазвичай розподілені із середнім значенням 68 і стандартне відхилення трьох. Знайдіть ймовірність того, що випадково обраний гольфіст набрав менше 65.

Відповідь

\(\text{normalcdf}(10^{99},65,68,3) = 0.1587\)

Приклад\(\PageIndex{3}\)

Персональний комп'ютер використовується для офісної роботи на дому, досліджень, спілкування, особистих фінансів, освіти, розваг, соціальних мереж і безлічі інших речей. Припустимо, що середня кількість годин використання побутового персонального комп'ютера для розваг становить дві години на добу. Припустимо, що час для розваг зазвичай розподілений, а стандартне відхилення для часу становить півгодини.

1. Знайдіть ймовірність того, що побутовий персональний комп'ютер використовується для розваг між 1,8 і 2,75 годинами на добу.
2. Знайдіть максимальну кількість годин на добу, яке нижній квартиль домочадців використовує персональний комп'ютер для розваг.

Відповідь

а. нехай\(X =\) кількість часу (в годинами) побутовий персональний комп'ютер використовується для розваг. \(X \sim N(2, 0.5)\)де\(\mu = 2\) і\(\sigma = 0.5\).

Знайти\(P(1.8 < x < 2.75)\).

Імовірність, за якою ви шукаєте, - це область між\(x = 1.8\) і\(x = 2.75\). \(P(1.8 < x < 2.75) = 0.5886\)

Малюнок\(\PageIndex{4}\).

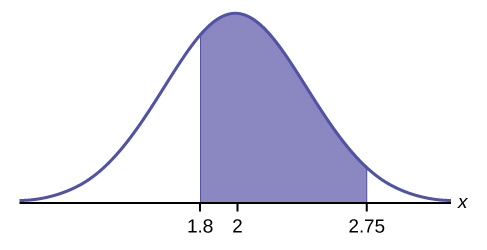
\[\text{normalcdf}(1.8,2.75,2,0.5) = 0.5886\nonumber \]

Імовірність того, що побутовий персональний комп'ютер використовується в межах від 1,8 до 2,75 годин на добу для розваг, становить 0,5886.

б.

Щоб знайти максимальну кількість годин на добу, яке нижній квартиль домочадців використовує персональний комп'ютер для розваг, знайдіть ^25-й процентиль\(k\), де\(P(x < k) = 0.25\).

Малюнок\(\PageIndex{5}\).

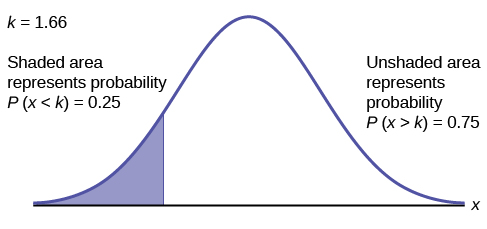
\[\text{invNorm}(0.25,2,0.5) = 1.66\nonumber \]

Максимальна кількість годин на добу, яке нижній квартиль домочадців використовує персональний комп'ютер для розваг, становить 1,66 години.

Вправа\(\PageIndex{3}\)

Гольф бали для шкільної команди були зазвичай розподілені із середнім значенням 68 і стандартне відхилення трьох. Знайти ймовірність того, що гольфіст забив між 66 і 70.

Відповідь

\(\text{normalcdf}(66,70,68,3) = 0.4950\)

Приклад\(\PageIndex{4}\)

Сьогодні у світі налічується приблизно один мільярд користувачів смартфонів. У США вік від 13 до 55+ користувачів смартфонів приблизно дотримується нормального розподілу з приблизним середнім і стандартним відхиленням в 36,9 років і 13,9 років відповідно.

1. Визначте ймовірність того, що випадковий користувач смартфона у віковому діапазоні від 13 до 55+ становить від 23 до 64,7 років.
2. Визначте ймовірність того, що випадково обраний користувач смартфона у віковому діапазоні від 13 до 55+ становить не більше 50,8 років.
3. Знайдіть ^80-й процентиль цього розподілу і інтерпретуйте його в повному реченні.

Відповідь

1. \(\text{normalcdf}(23,64.7,36.9,13.9) = 0.8186\)
2. \(\text{normalcdf}(-10^{99},50.8,36.9,13.9) = 0.8413\)
3. \(\text{invNorm}(0.80,36.9,13.9) = 48.6\)

^80-й процентиль становить 48,6 років.

80% користувачів смартфонів у віковому діапазоні 13 — 55+ — 48,6 років або менше.

Використовуйте інформацію в прикладі, щоб відповісти на наступні запитання.

Вправа\(\PageIndex{4}\)

1. Знайдіть ^30-й процентиль і інтерпретуйте його в повному реченні.
2. Яка ймовірність того, що вік випадково обраного користувача смартфона в діапазоні від 13 до 55+ менше 27 років.

70.

Відповідь

Нехай\(X =\) користувач смарт-телефону, вік якого становить від 13 до 55+. \(X \sim N(36.9, 13.9)\)

Щоб знайти ^30-й процентиль, знайдіть\(k\) такий, що\(P(x < k) = 0.30\).
\(\text{invNorm}(0.30, 36.9, 13.9) = 29.6\)років
Тридцять відсотків користувачів смартфонів від 13 до 55+ - не більше 29,6 років, а 70% - не менше 29,6 років. Знайти\(P(x < 27)\)

(Зауважте, що\(\text{normalcdf}(-10^{99},27,36.9,13.9) = 0.2382\). Дві відповіді відрізняються лише на 0,0040.)

Малюнок\(\PageIndex{6}\).

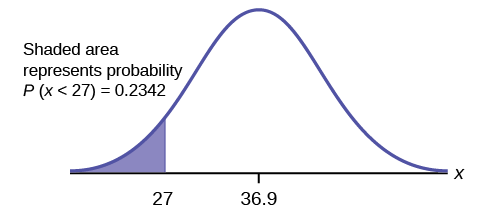
\[\text{normalcdf}(0,27,36.9,13.9) = 0.2342\nonumber \]

Приклад\(\PageIndex{5}\)

У Сполучених Штатах віком від 13 до 55+ користувачів смартфонів приблизно дотримуються нормального розподілу з приблизним середнім і стандартним відхиленням 36,9 років і 13,9 років відповідно. Використовуючи цю інформацію, дайте відповідь на наступні питання (круглі відповіді до одного знака після коми).

1. Обчисліть інтерквартильний діапазон (\(IQR\)).
2. Сорок відсотків вікових груп, які коливаються від 13 до 55+, принаймні якого віку?

Відповідь

а.

\[IQR = Q_{3} – Q_{1}\nonumber \]

Обчисліть\(Q_{3} =\) ^75-й процентиль і\(Q_{1} =\) ^25-й процентиль.

\[ \begin{align*} \text{invNorm}(0.75,36.9,13.9) &= Q_{3} = 46.2754 \\[4pt] \text{invNorm}(0.25,36.9,13.9) &= Q_{1} = 27.5246 \\[4pt] IQR &= Q_{3} - Q_{1} = 18.7508 \end{align*}\]

б.

Знайти\(k\) де\(P(x > k) = 0.40\) («Принаймні» перекладається як «більше або дорівнює».)

\(0.40 =\)область праворуч.

Область зліва\(= 1 – 0.40 = 0.60\).

Площа зліва від\(k = 0.60\).

\(\text{invNorm}(0.60,36.9,13.9) = 40.4215\).

\(k = 40.42\).

Сорок відсотків користувачів смартфонів від 13 до 55+ не менше 40,4 років.

Вправа\(\PageIndex{5}\)

Дві тисячі студентів склали іспит. Бали на іспиті мають приблизний нормальний розподіл із середніми балами і\(\mu = 81\) балами стандартного відхилення\(\sigma = 15\).

1. Обчисліть бали першого та третього квартилів для цього іспиту.
2. Середні 50% балів іспиту знаходяться між якими двома значеннями?

Відповідь

1. \(Q_{1} =\)^25-й процентиль\(= \text{invNorm}(0.25,81,15) = 70.9\)
   \(Q_{3} =\) ^75-й процентиль\(= \text{invNorm}(0.75,81,15) = 91.9\)
2. Середні 50% балів знаходяться між 70,9 і 91,1.

Приклад\(\PageIndex{6}\)

Фермер цитрусових, який вирощує мандаринові апельсини, виявляє, що діаметри мандаринових апельсинів, заготовлених на його фермі, дотримуються нормального розподілу із середнім діаметром 5,85 см і стандартним відхиленням 0,24 см.

1. Знайдіть ймовірність того, що випадково обраний мандарин з цієї ферми має діаметр більше 6,0 см. Намалюйте графік.
2. Середні 20% мандаринових апельсинів з цієї ферми мають діаметри між ______ і ______.
3. Знайдіть ^90-й процентиль для діаметрів мандаринових апельсинів і інтерпретуйте його в повному реченні.

Відповідь

а.\(\text{normalcdf}(6,10^{99},5.85,0.24) = 0.2660\)

Малюнок\(\PageIndex{7}\).

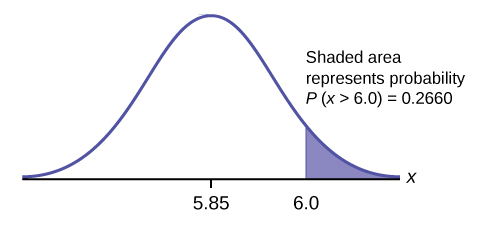
Відповідь

б.

\(1 – 0.20 = 0.80\)

Хвости графа нормального розподілу кожен мають площу 0,40.

Знайдіть\(k1\), ^40-й процентиль, а\(k2\), ^60-й процентиль (\(0.40 + 0.20 = 0.60\)).

\(k1 = \text{invNorm}(0.40,5.85,0.24) = 5.79\)см

\(k2 = \text{invNorm}(0.60,5.85,0.24) = 5.91\)см

Відповідь

c. 6,16: Дев'яносто відсотків діаметра мандаринових апельсинів становить не більше 6,15 см.

Вправа\(\PageIndex{6}\)

Використовуючи інформацію з Example, дайте відповідь на наступне:

1. Середні 45% мандаринових апельсинів з цієї ферми знаходяться між ______ і ______.
2. Знайдіть ^16-й процентиль і інтерпретуйте його в повному реченні.

Відповідь на

Середня область\(= 0.40\), тому кожен хвостик має площу 0,30.

\( – 0.40 = 0.60\)

Хвости графа нормального розподілу кожен мають площу 0,30.

Знайдіть\(k1\), ^30-й процентиль і\(k2\), ^70-й процентиль (\(0.40 + 0.30 = 0.70\)).

\(k1 = \text{invNorm}(0.30,5.85,0.24) = 5.72\)см

\(k2 = \text{invNorm}(0.70,5.85,0.24) = 5.98\)см

Відповідь б

\(\text{normalcdf}(5,10^{99},5.85,0.24) = 0.9998\)

Посилання

1. «Правило Наегеле». Вікіпедія. Доступно в Інтернеті за адресою http://en.Wikipedia.org/wiki/Naegele's_rule (доступ до 14 травня 2013 р.).
2. «403: НУМІ». Чиказькі громадські медіа та Іра Гласс, 2013. Доступний в Інтернеті за адресою www.thisamericanlife.org/радіо... сода/403/нумі (доступ до травня 14, 2013).
3. «Поради щодо гри в лотерейні квитки». Перемога в лотереї 2013. Доступний в Інтернеті за адресою www.winatlottery.com/publi... partment40.cfm (доступ до 14 травня 2013).
4. «Користувачі смартфонів, за номерами». Візуал.ли, 2013. Доступно в Інтернеті за адресою http://visual.ly/smart-phone-users-numbers (доступ до 14 травня 2013 р.).
5. «Статистика Facebook». Статистика мозку. Доступно в Інтернеті за адресою http://www.statisticbrain.com/facebo...tics/(accessed 14 травня 2013 р.).

Рецензія

Нормальний розподіл, який є безперервним, є найважливішим з усіх розподілів ймовірностей. Графік його має дзвоноподібну форму. Ця дзвіноподібна крива використовується практично у всіх дисциплін. Оскільки це безперервний розподіл, то загальна площа під кривою одна. Параметри нормалі - середнє\(\mu\) і стандартне відхилення σ. Особливим нормальним розподілом, званим стандартним нормальним розподілом, є розподіл z -балів. Його середнє значення дорівнює нулю, а стандартне відхилення - одиниця.

Огляд формули

• Нормальний розподіл:\(X \sim N(\mu, \sigma)\) де\(\mu\) середнє, а σ - стандартне відхилення.
• Стандартний нормальний розподіл:\(Z \sim N(0, 1)\).
• Функція калькулятора ймовірності:\(x\) normalcdf (нижнє значення площі, верхнє\(x\) значення площі, середнє, стандартне відхилення)
• Функція калькулятора для\(k\) ^го процентиля:\(k = \text{invNorm}\) (площа зліва від\(k\), середнє, стандартне відхилення)

Вправа\(\PageIndex{7}\)

Як би ви представляли область зліва від одного в заяві про ймовірність?

Малюнок\(\PageIndex{8}\).

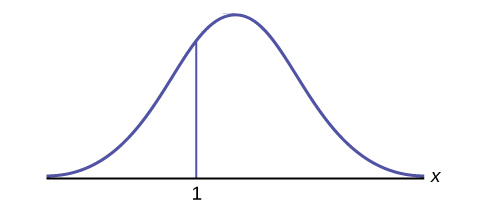
Відповідь

\(P(x < 1)\)

Вправа\(\PageIndex{8}\)

Чи\(P(x < 1)\) дорівнює\(P(x \leq 1)\)? Чому?

Відповідь

Так, тому що вони однакові в безперервному розподілі:\(P(x = 1) = 0\)

Вправа\(\PageIndex{9}\)

Як би ви представляли область зліва від трьох у заяві про ймовірність?

Малюнок\(\PageIndex{10}\).

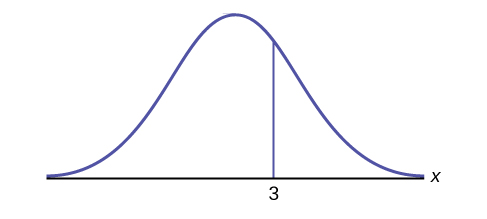
Вправа\(\PageIndex{10}\)

Яка площа праворуч від трьох?

Малюнок\(\PageIndex{11}\).

Відповідь

\(1 – P(x < 3)\)або\(P(x > 3)\)

Вправа\(\PageIndex{11}\)

Якщо область зліва від\(x\) нормального розподілу дорівнює 0,123, яка область праворуч від\(x\)?

Вправа\(\PageIndex{12}\)

Якщо область праворуч від\(x\) нормального розподілу дорівнює 0,543, яка область зліва від\(x\)?

Відповідь

\(1 - 0.543 = 0.457\)

Використовуйте наступну інформацію, щоб відповісти на наступні чотири вправи:

\(X \sim N(54, 8)\)

Вправа\(\PageIndex{13}\)

Знайдіть ймовірність того, що\(x > 56\).

Вправа\(\PageIndex{14}\)

Знайдіть ймовірність того, що\(x < 30\).

Відповідь

0,0013

Вправа\(\PageIndex{15}\)

Знайдіть ^80-й процентиль.

Вправа\(\PageIndex{16}\)

Знайдіть ^60-й процентиль.

Відповідь

56.03

Вправа\(\PageIndex{17}\)

\(X \sim N(6, 2)\)

Знайдіть ймовірність, що\(x\) знаходиться від трьох до дев'яти.

Вправа\(\PageIndex{18}\)

\(X \sim N(–3, 4)\)

Знайдіть ймовірність, що\(x\) знаходиться від одного до чотирьох.

Відповідь

0.1186

Вправа\(\PageIndex{19}\)

\(X \sim N(4, 5)\)

Знайдіть максимум\(x\) в нижньому квартилі.

Вправа\(\PageIndex{20}\)

Використовуйте наступну інформацію, щоб відповісти на наступні три вправи: Життя програвачів компакт-дисків Sunshine зазвичай розподіляється із середнім значенням 4,1 року та стандартним відхиленням 1,3 року. Програвач компакт-дисків гарантується на три роки. Нас цікавить, скільки часу триває програвач компакт-дисків. Знайдіть ймовірність того, що програвач компакт-дисків зламається протягом гарантійного терміну.

1. Намалюйте ситуацію. Позначте та масштабуйте осі. Затіньте область, відповідну ймовірності.

   

   Малюнок\(\PageIndex{12}\).

   \(P(0 < x <\)____________\() =\) ___________ (Використовуйте нуль для мінімального значення\(x\).)

Відповідь

1. Перевірте рішення студента.
2. 3, 0.1979

Вправа\(\PageIndex{21}\)

Знайдіть ймовірність того, що програвач компакт-дисків прослужить від 2,8 до шести років.

1. Намалюйте ситуацію. Позначте та масштабуйте осі. Затіньте область, відповідну ймовірності.

   

   Малюнок\(\PageIndex{13}\).

   \(P(\)__________\(< x <\) __________\()\) = __________

Вправа\(\PageIndex{22}\)

Знайдіть ^70-й процентиль дистрибутива за час тривалості програвача компакт-дисків.

1. Намалюйте ситуацію. Позначте та масштабуйте осі. Затіньте область, відповідну нижнім 70%.

   

   Малюнок\(\PageIndex{14}\).

   \(P(x < k) =\)__________ Тому\(k =\) _________

Відповідь

1. Перевірте рішення студента.
2. 0,70, 4,78 років