2.8: Заходи поширення даних

Last updated
Save as PDF

Page ID: 98418

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Важливою характеристикою будь-якого набору даних є варіація даних. У деяких наборах даних значення даних зосереджені близько до середнього; в інших наборах даних значення даних більш поширені від середнього. Найпоширенішою мірою варіації, або спреду, є стандартне відхилення. Стандартне відхилення - це число, яке вимірює, наскільки далекі значення даних від їх середнього.

стандартне відхилення

забезпечує числовий показник загальної кількості варіацій у наборі даних, і
може використовуватися для визначення того, чи є конкретне значення даних близьким до середнього або далеким від нього.

Стандартне відхилення забезпечує міру загальної варіації в наборі даних

Стандартне відхилення завжди позитивне або нульове. Стандартне відхилення невелике, коли всі дані зосереджені близько до середнього, демонструючи незначні зміни або поширення. Стандартне відхилення більше, коли значення даних більш поширені від середнього, проявляючи більше варіацій.

Припустимо, що ми вивчаємо кількість часу очікування клієнтів в черзі на касі в супермаркеті А і супермаркеті Б. Середній час очікування в обох супермаркетах становить п'ять хвилин. У супермаркеті А стандартне відхилення часу очікування становить дві хвилини; в супермаркеті B стандартне відхилення часу очікування становить чотири хвилини.

Оскільки супермаркет B має більш високе стандартне відхилення, ми знаємо, що в супермаркеті B більше варіацій часу очікування. Загалом, час очікування в супермаркеті B більш розподілений від середнього; час очікування в супермаркеті А більш концентрований поблизу середнього.

Стандартне відхилення може бути використано для визначення того, чи є значення даних близьким до середнього або далеким від нього.

Припустимо, що Роза і Бінь обидва магазини в супермаркеті А. Роза чекає біля каси сім хвилин, а Бінь чекає одну хвилину. У супермаркеті А середній час очікування становить п'ять хвилин, а стандартне відхилення - дві хвилини. Стандартне відхилення може бути використано для визначення того, чи є значення даних близьким до середнього або далеким від нього.

Роза чекає сім хвилин:

Сімка на дві хвилини довше, ніж в середньому п'ять; дві хвилини дорівнює одному стандартному відхиленню.
Час очікування Рози сім хвилин на дві хвилини довше, ніж в середньому п'ять хвилин.
Час очікування Рози сім хвилин - одне стандартне відхилення вище середнього на п'ять хвилин.

Бін чекає одну хвилину.

Одна на чотири хвилини менше середнього показника п'яти; чотири хвилини дорівнює двом стандартним відхиленням.
Час очікування Бінь на одну хвилину на чотири хвилини менше, ніж в середньому п'ять хвилин.
Час очікування Бінха в одну хвилину становить два стандартних відхилення нижче середнього показника п'яти хвилин.
Значення даних, яке є двома стандартними відхиленнями від середнього, знаходиться лише на межі того, що багато статистиків вважали б далеким від середнього. Враховуючи, що дані далекі від середнього, якщо це більше двох стандартних відхилень, це скоріше приблизне «правило», ніж жорстке правило. Загалом, форма розподілу даних впливає на те, скільки даних знаходиться далі, ніж два стандартні відхилення. (Ви дізнаєтеся більше про це в наступних розділах.)

Числовий рядок може допомогти вам зрозуміти стандартне відхилення. Якби ми поставили п'ять і сім на числовому рядку, сім праворуч від п'яти. Тоді ми говоримо, що сім є одним стандартним відхиленням праворуч від п'яти тому що\(5 + (1)(2) = 7\).

Якщо один також був частиною набору даних, то один - це два стандартних відхилення зліва від п'яти тому що\(5 + (-2)(2) = 1\).

Це показує числовий рядок з інтервалами 1 від 0 до 7. — Малюнок\(\PageIndex{1}\)

Загалом, значення = середнє + (#ofSTDEV) (стандартне відхилення)
де #ofSTDEVs = кількість стандартних відхилень
#ofSTDEV не обов'язково має бути цілим числом
Один - це два стандартних відхилення, менші за середнє значення п'яти, оскільки:\(1 = 5 + (-2)(2)\).

Значення рівняння = середнє + (#ofSTDEVs) (стандартне відхилення) може бути виражено як для вибірки, так і для сукупності.

зразок:\[x = \bar{x} + \text{(#ofSTDEV)(s)}\]
Населення:\[x = \mu + \text{(#ofSTDEV)(s)}\]

Нижня буква s представляє зразкове стандартне відхилення, а грецька буква\(\sigma\) (сигма, нижній регістр) - стандартне відхилення населення.

Символ\(\bar{x}\) є зразком середнього, а грецький символ\(\mu\) - середнє населення.

Розрахунок стандартного відхилення

Якщо\(x\) це число, то різниця «\(x\)— середнє» називається його відхиленням. У наборі даних існує стільки відхилень, скільки елементів у наборі даних. Відхилення використовуються для розрахунку стандартного відхилення. Якщо числа належать сукупності, в символах відхилення є\(x - \mu\). Для вибіркових даних в символах є відхилення\(x - \bar{x}\).

Процедура обчислення стандартного відхилення залежить від того, чи є цифрами вся сукупність або дані з вибірки. Розрахунки аналогічні, але не ідентичні. Тому символ, який використовується для представлення стандартного відхилення, залежить від того, обчислюється воно за сукупністю або вибіркою. Нижня буква s представляє зразкове стандартне відхилення, а грецька буква\(\sigma\) (сигма, нижній регістр) - стандартне відхилення населення. Якщо вибірка має ті ж характеристики, що і популяція, то s повинна бути хорошою оцінкою\(\sigma\).

Щоб розрахувати стандартне відхилення, нам потрібно спочатку обчислити дисперсію. Дисперсія - це середнє значення квадратів відхилень (\(x - \bar{x}\)значення для вибірки, або\(x - \mu\) значення для сукупності). Символ\(\sigma^{2}\) представляє дисперсію популяції; стандартне відхилення населення\(\sigma\) - квадратний корінь дисперсії популяції. Символ\(s^{2}\) представляє дисперсію зразка; стандартне відхилення зразка s - квадратний корінь дисперсії вибірки. Ви можете думати про стандартне відхилення як про особливе середнє значення відхилень.

Якщо цифри виходять з перепису всього населення, а не вибірки, коли ми обчислюємо середнє значення квадратних відхилень, щоб знайти дисперсію, ділимо на\(N\), кількість предметів в популяції. Якщо дані з вибірки, а не сукупності, то при обчисленні середнього квадрата відхилень ділимо на n — 1, на одиницю менше, ніж кількість елементів у вибірці.

Формули для зразка стандартного відхилення

\[s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}} \label{eq1}\]

або

\[s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}} \label{eq2}\]

Для зразка стандартного відхилення знаменником є\(n - 1\), тобто розмір вибірки МІНУС 1.

Формули для стандартного відхилення населення

\[\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}} \label{eq3} \]

або

\[\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}} \label{eq4}\]

Для популяції стандартне відхилення знаменником є\(N\), кількість предметів в популяції.

У рівняннях\ ref {eq2} і\ ref {eq4},\(f\) представляє частоту, з якою з'являється значення. Наприклад, якщо значення з'являється один раз,\(f\) є одиницею. Якщо значення з'являється тричі в наборі даних або населенні,\(f\) дорівнює трьом.

Варіабельність вибірки статистики

Статистика розподілу вибірки була розглянута в розділі 2.6. Наскільки статистика варіюється від однієї вибірки до іншої, відома як мінливість вибірки статистики. Зазвичай ви вимірюєте мінливість вибірки статистики за її стандартною помилкою.

Стандартна похибка середнього - приклад стандартної помилки. Це спеціальне стандартне відхилення і відоме як стандартне відхилення розподілу вибірки середнього. Ви покриєте стандартну помилку середнього значення в главі 7. Позначення стандартної похибки середнього значення -\(\sigma\) це\(\dfrac{\sigma}{\sqrt{n}}\) де стандартне відхилення сукупності і\(n\) розмір вибірки.

На практиці ВИКОРИСТОВУЙТЕ КАЛЬКУЛЯТОР АБО КОМП'ЮТЕРНЕ ПРОГРАМНЕ ЗАБЕЗПЕЧЕННЯ ДЛЯ РОЗРАХУНКУ СТАНДАРТНОГО ВІДХИЛЕННЯ. Якщо ви використовуєте калькулятор TI-83, 83+, 84+, потрібно вибрати відповідне стандартне відхилення\(\sigma_{x}\) або \(s_{x}\)з підсумкової статистики. Ми сконцентруємося на використанні та інтерпретації інформації, яку дає нам стандартне відхилення. Однак вам слід вивчити наступний покроковий приклад, щоб допомогти вам зрозуміти, як стандартне відхилення вимірює відхилення від середнього. (Інструкції з калькулятора відображаються в кінці цього прикладу.)

Приклад\(\PageIndex{1}\)

У п'ятому класі вчительку цікавив середній вік і вибірка стандартного відхилення вікових груп її учнів. Наступні дані - це вік для ЗРАЗКА n = 20 учнів п'ятого класу. Вік округляється до найближчого півроку:

9; 9,5; 9,5; 10; 10; 10; 10; 10; 10.5; 10,5; 10,5; 11; 11; 11; 11; 11; 11; 11; 11.5; 11.5; 11.5;

\[\bar{x} = \dfrac{9+9.5(2)+10(4)+10.5(4)+11(6)+11.5(3)}{20} = 10.525 \nonumber\]

Середній вік становить 10,53 року, округлений до двох місць.

Дисперсію можна обчислити за допомогою таблиці. Потім стандартне відхилення обчислюється, взявши квадратний корінь дисперсії. Ми пояснимо частини таблиці після обчислення s.

Дані	Фрек.	Відхилення	Відхилення ²	*(Фрек.) (Відхилення* ²)**
х	f	(х —\(\bar{x}\))	(х — 2\(\bar{x}\))	(f) (х —\(\bar{x}\)) 2
9	1	9 — 10,525 = —1,525	(—1,525) 2 = 2,325625	1 × 2,325625 = 2,325625
9.5	2	9.5 — 10,525 = —1.025	(—1.025) ² = 1.050625	2 × 1,050625 = 2,101250
10	4	10 — 10,525 = —0,525	(—0.525) ² = 0,275625	4 × 0,275625 = 1,1025
10.5	4	10.5 — 10,525 = —0,025	(—0,025) ² = 0,000625	4 × 0,000625 = 0,0025
11	6	1 - 10,525 = 0,475	(0,475) ² = 0,225625	6 × 0,225625 = 1,35375
11.5	3	11.5 — 10,525 = 0,975	(0,975) ² = 0,950625	3 × 0,950625 = 2,851875
				Загальна сума становить 9.7375

Вибіркова дисперсія\(s^{2}\) дорівнює сумі останнього стовпця (9.7375), поділеної на загальну кількість значень даних мінус один (20 — 1):

\[s^{2} = \dfrac{9.7375}{20-1} = 0.5125 \nonumber\]

Стандартне відхилення зразка s дорівнює квадратному кореню дисперсії зразка:

\[s = \sqrt{0.5125} = 0.715891 \nonumber\]

і це округляється до двох знаків після коми,\(s = 0.72\).

Як правило, ви робите розрахунок для стандартного відхилення на вашому калькуляторі або комп'ютері. Проміжні результати не округляються. Це робиться для точності.

Для наступних проблем нагадайте, що значення = середнє + (#ofSTDEVs) (стандартне відхилення). Перевірте середнє і стандартне відхилення або калькулятор або комп'ютер.
Для зразка:\(x\) =\(\bar{x}\) + (#ofSTDEVs) (s)
Для населення:\(x\) =\(\mu\) + (#ofSTDEVs)\(\sigma\)
Для цього прикладу використовуйте x =\(\bar{x}\) + (#ofSTDEVs) (s), оскільки дані взяті з вибірки

Перевірте середнє і стандартне відхилення на калькуляторі або комп'ютері.
Знайдіть значення, яке є одним стандартним відхиленням вище середнього. Знайти (\(\bar{x}\)+ 1s).
Знайдіть значення, яке є двома стандартними відхиленнями нижче середнього. Знайти (\(\bar{x}\)— 2с).
Знайдіть значення, які становлять 1,5 стандартних відхилень від (нижче і вище) середнього.

Рішення

- Очистити списки L1 і L2. Натисніть СТАТ 4: CLRList. Введіть 2-й 1 для L1, кому (,) та 2-й 2 для L2.
- Введіть дані в редактор списків. Натисніть СТАТ 1: РЕДАГУВАТИ. При необхідності очистіть списки стрілкою вгору в ім'я. Натисніть CLEAR і стрілку вниз.
- Помістіть значення даних (9, 9,5, 10, 10.5, 11, 11.5) у список L1 та частоти (1, 2, 4, 4, 6, 3) у список L2. використовувати клавіші зі стрілками для переміщення.
- Натисніть STAT і стрілку до CALC. Натисніть 1:1 -VARStats і введіть L1 (2-й 1), L2 (2-й 2). Не забувайте про кому. Натисніть клавішу ENTER.
- \(\bar{x}\)= 10,525
- Використовуйте Sx, оскільки це вибіркові дані (а не сукупність): Sx = 0.715891
(\(\bar{x} + 1s) = 10.53 + (1)(0.72) = 11.25\)
\((\bar{x} - 2s) = 10.53 – (2)(0.72) = 9.09\)
- \((\bar{x} - 1.5s) = 10.53 – (1.5)(0.72) = 9.45\)
- \((\bar{x} + 1.5s) = 10.53 + (1.5)(0.72) = 11.61\)

Вправа 2.8.1

У бейсбольній команді вік кожного з гравців такий:

21; 21; 22; 23; 24; 24; 25; 25; 28; 29; 29; 31; 32; 33; 34; 35; 36; 36; 36; 36; 38; 38; 38; 38; 38; 40

Використовуйте калькулятор або комп'ютер, щоб знайти середнє і стандартне відхилення. Потім знайдіть значення, яке є двома стандартними відхиленнями вище середнього.

Відповідь

\(\mu\)= 30,68

\(s = 6.09\)

(\(\bar{x} + 2s = 30.68 + (2)(6.09) = 42.86\).

Розшифровка розрахунку стандартного відхилення наведено в таблиці

Відхилення показують, наскільки розкидані дані про середнє значення. Значення даних 11,5 знаходиться далі від середнього, ніж є значенням даних 11, яке позначається відхиленнями 0,97 і 0,47. Позитивне відхилення виникає, коли значення даних більше середнього, тоді як негативне відхилення виникає, коли значення даних менше середнього. Відхилення становить —1.525 для значення даних дев'ять. Якщо скласти відхилення, сума завжди дорівнює нулю. (Наприклад\(\PageIndex{1}\), є\(n = 20\) відхилення.) Таким чином, ви не можете просто додати відхилення, щоб отримати розкид даних. Склавши відхилення в квадрат, ви робите з них позитивні числа, причому сума теж буде позитивною. Отже, дисперсія - це середнє квадратне відхилення.

Дисперсія - це квадратна міра і не має тих самих одиниць, що і дані. Взяття квадратного кореня вирішує проблему. Стандартне відхилення вимірює розкид в тих же одиницях, що і дані.

Зверніть увагу, що замість того\(n = 20\), щоб ділити на, розрахунок ділиться на\(n - 1 = 20 - 1 = 19\) тому, що дані є зразком. Для дисперсії вибірки ділимо на розмір вибірки мінус одиниця (\(n - 1\)). Чому б не розділити на\(n\)? Відповідь пов'язана з дисперсією населення. Дисперсія вибірки - це оцінка дисперсії популяції. Виходячи з теоретичної математики, яка лежить за цими розрахунками, ділення на (\(n - 1\)) дає кращу оцінку дисперсії популяції.

Ваша концентрація повинна бути на тому, що стандартне відхилення говорить нам про дані. Стандартне відхилення - це число, яке вимірює, наскільки дані поширюються від середнього. Нехай калькулятор або комп'ютер робити арифметику.

Стандартне відхилення\(\sigma\),\(s\) або, дорівнює нулю або більше нуля. Коли стандартне відхилення дорівнює нулю, розкиду немає; тобто всі значення даних рівні один одному. Стандартне відхилення невелике, коли всі дані зосереджені близько до середнього, і більше, коли значення даних показують більше відмінностей від середнього. Коли стандартне відхилення набагато більше нуля, значення даних дуже розподілені щодо середнього; викиди можуть зробити\(s\) або\(\sigma\) дуже великі.

Стандартне відхилення при першому представленні може здатися неясним. Розміщуючи свої дані, ви можете краще «відчути» відхилення та стандартне відхилення. Ви побачите, що в симетричних розподілах стандартне відхилення може бути дуже корисним, але в перекосованих розподілах стандартне відхилення може не сильно допомогти. Причина полягає в тому, що дві сторони перекошеного розподілу мають різні розвороти. При перекошеному розподілі краще дивитися на перший квартиль, медіану, третій квартиль, найменше значення і найбільше значення. Оскільки цифри можуть збивати з пантелику, завжди графуйте свої дані. Відображення даних у гістограмі або графіку коробки.

Приклад\(\PageIndex{2}\)

Використовуйте наступні дані (перші бали іспиту) з весняного попереднього обчислення класу Сьюзен Дін:

33; 42; 49; 49; 53; 55; 55; 61; 63; 67; 68; 68; 69; 69; 72; 73; 74; 78; 80; 83; 88; 88; 90; 92; 94; 94; 94; 94; 94; 94; 94; 96; 100

Створіть діаграму, що містить дані, частоти, відносні частоти та сукупні відносні частоти до трьох знаків після коми.
Обчисліть наступне до одного знака після коми за допомогою калькулятора TI-83+ або TI-84:
1. Середнє значення зразка
2. Зразок стандартного відхилення
3. Медіана
4. Перший квартиль
5. Третій квартиль
6. IQR
Побудувати квадратний графік і гістограму на одному наборі осей. Зробіть коментарі щодо графіка коробки, гістограми та діаграми.

Відповідь

Див. таблицю
1. Середнє значення зразка = 73,5
2. Вибірка стандартного відхилення = 17,9
3. Медіана = 73
4. Перший квартиль = 61
5. Третій квартиль = 90
6. ІКР = 90 — 61 = 29
\(x\)-вісь йде від 32.5 до 100.5;\(y\) -вісь йде від -2.4 до 15 для гістограми. Кількість інтервалів - п'ять, тому ширина інтервалу (\(100.5 - 32.5\)) ділиться на п'ять, дорівнює 13,6. Кінцеві точки інтервалів такі: початкова точка - 32,5,,,,\(32.5 + 13.6 = 46.1\),\(46.1 + 13.6 = 59.7\)\(59.7 + 13.6 = 73.3\)\(73.3 + 13.6 = 86.9\),\(86.9 + 13.6 = 100.5 =\) кінцеве значення; жодні значення даних не потрапляють на межу інтервалу.

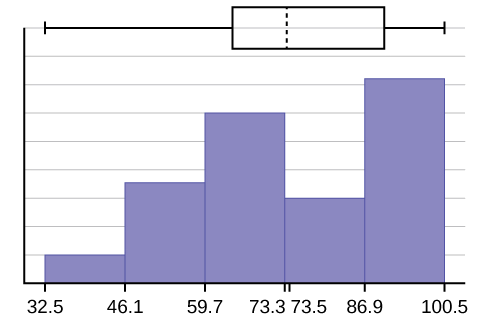
Гібридне зображення, що відображає як гістограму, так і рамковий графік, детально описаний у вирішенні відповіді вище. — Малюнок\(\PageIndex{2}\).

Довгий лівий вус на графіку коробки відображається в лівій частині гістограми. Розкид балів іспиту в нижніх 50% більше (\(73 - 33 = 40\)), ніж спред у верхніх 50% (\(100 - 73 = 27\)). Гістограма, діаграма та діаграма відображають це. Існує значна кількість класів А та В (80-ті, 90-ті та 100). Гістограма наочно це показує. Графік коробки показує нам, що середні 50% балів іспиту (IQR = 29) - це Ds, Cs та Bs. Графік коробки також показує нам, що нижчі 25% балів іспиту - це Ds та Fs.

Дані	Частота	Відносна частота	Накопичувальна відносна частота
33	1	0.032	0.032
42	1	0.032	0.064
49	2	0.065	0.129
53	1	0.032	0.161
55	2	0.065	0,226
61	1	0.032	0,258
63	1	0.032	0,29
67	1	0.032	0,322
68	2	0.065	0,387
69	2	0.065	0,452
72	1	0.032	0,484
73	1	0.032	0.516
74	1	0.032	0.548
78	1	0.032	0,580
80	1	0.032	0.612
83	1	0.032	0.644
88	3	0.097	0,741
90	1	0.032	0.773
92	1	0.032	0,805
94	4	0.129	0,934
96	1	0.032	0,966
100	1	0.032	0.998 (Чому це значення не 1?)

Вправа\(\PageIndex{2}\)

Наступні дані показують різні типи магазинів кормів для домашніх тварин у цьому районі.

6; 6; 6; 6; 7; 7; 7; 7; 7; 8; 9; 9; 9; 9; 10; 10; 10; 10; 10; 11; 11; 11; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12;

Обчисліть середнє значення вибірки та стандартне відхилення зразка до одного знака після коми за допомогою калькулятора TI-83+ або TI-84.

Відповідь

\(\mu = 9.3\)і\(s = 2.2\)

Стандартне відхилення згрупованих таблиць частот

Нагадаємо, що для згрупованих даних ми не знаємо окремих значень даних, тому ми не можемо описати типове значення даних з точністю. Іншими словами, ми не можемо знайти точне середнє значення, медіану або режим. Однак ми можемо визначити найкращу оцінку мір центру, знайшовши середнє значення згрупованих даних за формулою:

\[\text{Mean of Frequency Table} = \dfrac{\sum fm}{\sum f}\]

де\(f\) інтервальні частоти і\(m =\) проміжні середні точки.

Подібно до того, як ми не змогли знайти точне середнє значення, ми також не можемо знайти точне стандартне відхилення. Пам'ятайте, що стандартне відхилення описує чисельно очікуване відхилення, яке має значення даних від середнього. У простій англійській мові стандартне відхилення дозволяє порівняти, наскільки «незвичайні» окремі дані порівнюються із середнім значенням.

Приклад\(\PageIndex{3}\)

Знайдіть стандартне відхилення для даних в табл\(\PageIndex{3}\).

Таблиця\(\PageIndex{3}\)
Клас	Частота, f	Середня точка, м	м ²	\(\bar{x}\)	фм ²	Стандартне відхилення
0—2	1	1	1	\ (\ bar {x}\)» style="вертикальне вирівнювання: середина; ">7.58	1	3.5
3—5	6	4	16	\ (\ bar {x}\)» style="вертикальне вирівнювання: середина; ">7.58	96	3.5
6—8	10	7	49	\ (\ bar {x}\)» style="вертикальне вирівнювання: середина; ">7.58	490	3.5
9-11	7	10	100	\ (\ bar {x}\)» style="вертикальне вирівнювання: середина; ">7.58	700	3.5
12—14	0	13	169	\ (\ bar {x}\)» style="вертикальне вирівнювання: середина; ">7.58	0	3.5
15—17	2	16	256	\ (\ bar {x}\)» style="вертикальне вирівнювання: середина; ">7.58	512	3.5

Для цього набору даних ми маємо середнє значення,\(\bar{x}\) = 7,58 і стандартне відхилення,\(s_{x}\) = 3,5. Це означає, що випадково вибране значення даних, як очікується, становитиме 3,5 одиниці від середнього. Якщо ми подивимося на перший клас, то побачимо, що середина класу дорівнює одиниці. Це майже два повних стандартних відхилення від середнього значення, починаючи з 7,58 — 3,5 — 3,5 = 0,58. У той час як формула розрахунку стандартного відхилення не є складною,\(s_{x} = \sqrt{\dfrac{f(m - \bar{x})^{2}}{n-1}}\) де\(s_{x}\) = стандартне відхилення вибірки,\(\bar{x}\) = середнє значення вибірки, обчислення є виснажливими. Зазвичай найкраще використовувати технологію при виконанні розрахунків.

Знайдіть стандартне відхилення для даних з попереднього прикладу

Клас	0-2	3-5	6-8	9-11	12—14	15—17
Частота, f	1	6	10	7	0	2

Спочатку натисніть клавішу STAT і виберіть 1: Змінити

Введіть значення середньої точки в L1 і частоти в L2

Виберіть STAT, CALC та Статистика 1:1-Var

Виберіть ^2-й потім 1 потім, ^2-й потім 2 Введіть

Ви побачите, що відображається як стандартне відхилення населення\(\sigma_{x}\), так і стандартне відхилення вибірки\(s_{x}\).

Порівняння значень з різних наборів даних

Стандартне відхилення корисно при порівнянні значень даних, що надходять з різних наборів даних. Якщо набори даних мають різні засоби і стандартні відхилення, то порівняння значень даних безпосередньо може ввести в оману.

Для кожного значення даних розрахуйте, скільки стандартних відхилень від його середнього значення.
Використовуйте формулу: значення = середнє + (#ofSTDEVs) (стандартне відхилення); вирішити для #ofSTDEVs.
\(\text{#ofSTDEVs} = \dfrac{\text{value-mean}}{\text{standard deviation}}\)
Порівняйте результати цього розрахунку.

#ofSTDEVs часто називають «z -score»; ми можемо використовувати символ\(z\). У символах формули стають:

Зразок	\(x = \bar{x} + zs\)	\(z = \dfrac{x - \bar{x}}{s}\)
Населення	\(x = \mu + z\sigma\)	\(z = \dfrac{x - \mu}{\sigma}\)

Приклад\(\PageIndex{4}\)

Двоє учнів, Джон та Алі, з різних середніх шкіл, хотіли з'ясувати, хто мав найвищий середній бал порівняно зі своєю школою. Який учень мав найвищий середній бал у порівнянні зі своєю школою?

Студент	ГПа	Середній середній середній бал	Шкільне стандартне відхилення
Джон	2.85	3.0	0.7
Алі	77	80	10

Відповідь

Для кожного учня визначте, скільки стандартних відхилень (#ofSTDEVs) його середній бал подалі від середнього, для його школи. Звертайте пильну увагу на ознаки при порівнянні і тлумаченні відповіді.

\[z = \text{#ofSTDEVs} = \left(\dfrac{\text{value-mean}}{\text{standard deviation}}\right) = \left(\dfrac{x + \mu}{\sigma}\right) \nonumber\]

Для Джона,

\[z = \text{#ofSTDEVs} = \left(\dfrac{2.85-3.0}{0.7}\right) = -0.21 \nonumber\]

Для Алі,

\[z = \text{#ofSTDEVs} = (\dfrac{77-80}{10}) = -0.3 \nonumber\]

Джон має кращий середній бал порівняно зі своєю школою, оскільки його середній бал становить 0,21 стандартних відхилень нижче середнього рівня своєї школи, тоді як середній бал Алі становить 0,3 стандартних відхилень нижче середнього рівня його школи.

Z -оцінка Джона —0,21 вище, ніж z -оцінка Алі —0,3. Для GPA вищі значення кращі, тому ми робимо висновок, що Джон має кращий середній бал порівняно зі своєю школою.

Вправа\(\PageIndex{4}\)

Двоє плавців, Енджі та Бет, з різних команд, хотіли з'ясувати, хто мав найшвидший час для 50 метрів вільним стилем порівняно з її командою. Який плавець мав найшвидший час у порівнянні зі своєю командою?

Плавець	Час (секунди)	Командний середній час	Стандартне відхилення команди
Енджі	26.2	27.2	0.8
Бет	27.3	30.1	1.4

Відповідь

Для Енджі:

\[z = \left(\dfrac{26.2-27.2}{0.8}\right) = -1.25 \nonumber\]

Для Бет:

\[z = \left(\dfrac{27.3-30.1}{1.4}\right) = -2 \nonumber\]

Наступні списки дають кілька фактів, які дають трохи більше розуміння того, що стандартне відхилення говорить нам про розподіл даних.

Для БУДЬ-ЯКОГО набору даних, незалежно від того, який розподіл даних:

Не менше 75% даних знаходиться в межах двох стандартних відхилень від середнього.
Щонайменше 89% даних знаходиться в межах трьох стандартних відхилень від середнього.
Не менше 95% даних знаходиться в межах 4,5 стандартних відхилень від середнього.
Це відоме як Правило Чебишева.

Для даних, що мають розподіл, який є дзвоноподібним і СИМЕТРИЧНИМ:

Приблизно 68% даних знаходиться в межах одного стандартного відхилення від середнього.
Приблизно 95% даних знаходиться в межах двох стандартних відхилень від середнього.
Понад 99% даних знаходиться в межах трьох стандартних відхилень від середнього.
Це відоме як емпіричне правило.
Важливо відзначити, що це правило застосовується тільки тоді, коли форма розподілу даних має дзвоноподібну і симетричну форму. Детальніше про це ми дізнаємося, вивчаючи «Нормальний» або «Гауссовий» розподіл ймовірностей в наступних розділах.

Посилання

Дані з книжкової полиці Microsoft.
Король, Білл. «Графічно кажучи». Інституційні дослідження, громадський коледж озера Тахо. Доступний в Інтернеті за адресою www.ltcc.edu/web/про/інституційно-дослідницька (доступ до квітня 3, 2013).

Рецензія

Стандартне відхилення може допомогти вам розрахувати розкид даних. Існують різні рівняння, які слід використовувати, якщо обчислюють стандартне відхилення вибірки або популяції.

Стандартне відхилення дозволяє нам порівнювати окремі дані або класи з середнім чисельним числовим значенням набору даних.
\(s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}}\)або\(s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}}\) - формула розрахунку стандартного відхилення вибірки. Щоб обчислити стандартне відхилення населення, ми використовували б середнє значення популяції\(\mu\), і формулу\(\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}}\) або\(\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}}\). ↑ f (x − μ) 2 N − − − − − − − − − − √.

Огляд формули

\[s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^2}\]

де\(s_{x} \text{sample standard deviation}\) і\(\bar{x} = \text{sample mean}\)

Використовуйте наступну інформацію, щоб відповісти на наступні дві вправи: Наступні дані - це відстані між 20 роздрібними магазинами та великим розподільним центром. Відстані вказані в милі.

29; 37; 38; 40; 58; 67; 68; 69; 76; 86; 87; 95; 96; 99; 106; 112; 127; 145; 150

Вправа 2.8.4

Використовуйте графічний калькулятор або комп'ютер, щоб знайти стандартне відхилення і округлити до найближчої десятої.

Відповідь

\(s\)= 34,5

Вправа 2.8.5

Знайдіть значення, яке є одним стандартним відхиленням нижче середнього.

Вправа 2.8.6

Два бейсболісти, Фредо і Карл, на різних командах хотіли з'ясувати, хто мав вищий середній ватин у порівнянні зі своєю командою. Який гравець у бейсбол мав вищий середній ватин у порівнянні зі своєю командою?

Бейсболіст	Ватин середній	Середня команда ватин	Стандартне відхилення команди
Фредо	0.158	0.166	0.012
Карл	0.177	0.189	0,015

Відповідь

Для Фредо:

\(z\)\(\dfrac{0.158-0.166}{0.012}\)= —0,67

Для Карла:

\(z\)\(\dfrac{0.177-0.189}{0.015}\)= -0.8

Z-оцінка Фредо —0,67 вище, ніж z -оцінка Карла —0,8. Для середнього ватину вищі значення кращі, тому Фредо має кращий середній рівень ватину порівняно зі своєю командою.

Вправа 2.8.7

Використовуйте таблицю, щоб знайти значення, яке є трьома стандартними відхиленнями:

вище середнього
нижче середнього

Знайдіть стандартне відхилення для наступних таблиць частот, використовуючи формулу. Перевірте розрахунки з ТІ 83/84.

Вправа 2.8.5

Сорт	Частота
49.5—59,5	2
59.5—69.5	3
69.5—79.5	8
79.5—89.5	12
89.5—99.5	5

Щоденна низька температура	Частота
49.5—59,5	53
59.5—69.5	32
69.5—79.5	15
79.5—89.5	1
89.5—99.5	0

Очки за гру	Частота
49.5—59,5	14
59.5—69.5	32
69.5—79.5	15
79.5—89.5	23
89.5—99.5	2

Відповідь

\(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{193157.45}{30} - 79.5^{2}} = 10.88\)
\(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{380945.3}{101} - 60.94^{2}} = 7.62\)
\(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{440051.5}{86} - 70.66^{2}} = 11.14\)

З'єднавши його разом

Вправа 2.8.7

Двадцять п'ять випадково відібраних студентів запитали про кількість фільмів, які вони переглянули за попередній тиждень. Результати такі:

Кількість фільмів	Частота
0	5
1	9
2	6
3	4
4	1

Знайдіть зразок середнього значення\(\bar{x}\).
Знайти приблизну вибірку стандартного відхилення,\(s\).

Відповідь

1.48
1.12

Вправа 2.8.8

Сорок випадково відібраних студентів запитали про кількість пар кросівок, якими вони володіли. Нехай\(X =\) кількість пар кросівок належить. Результати такі:

\(X\)	Частота по
\ (X\) ">1	2
\ (X\) ">2	5
\ (X\) ">3	8
\ (X\) ">4	12
\ (X\) ">5	12
\ (X\) ">6	0
\ (X\) ">7	1

Знайти середнє значення зразка\(\bar{x}\)
Знаходимо стандартне відхилення зразка, с
Побудувати гістограму даних.
Заповніть стовпці діаграми.
Знайдіть перший квартиль.
Знайдіть медіану.
Знайдіть третій квартиль.
Побудувати квадратний графік даних.
Який відсоток учнів володів щонайменше п'ятьма парами?
Знайдіть ^40-й процентиль.
Знайдіть ^90-й процентиль.
Побудувати лінійний графік даних
Побудувати стовбур даних

Вправа 2.8.9

Нижче наведені опубліковані ваги (в фунтах) всіх членів команди Сан-Франциско 49ers з попереднього року.

177; 205; 210; 210; 232; 205; 185; 178; 210; 206; 212; 184; 174; 185; 242; 212; 215; 241; 223; 220; 260; 245; 259; 278; 270; 280; 290; 272; 280; 285; 200; 215; 230; 250; 241; 190; 260; 250; 302; 265; 290; 276; 228; 265

Організуйте дані від найменшого до найбільшого значення.
Знайдіть медіану.
Знайдіть перший квартиль.
Знайдіть третій квартиль.
Побудувати квадратний графік даних.
Середні 50% ваг складають від _______ до _______.
Якби наше населення було все професійними футболістами, чи були б наведені вище дані вибіркою ваг або популяцією ваг? Чому?
Якби наше населення включало кожного члена команди, який коли-небудь грав за Сан-Франциско 49ers, чи були б наведені вище дані вибіркою ваг або населення ваг? Чому?
Припустимо, населення Сан-Франциско становило 49ers. Знайти:
1. населення означає,\(\mu\).
2. стандартне відхилення населення,\(\sigma\).
3. вага, який на два стандартних відхилення нижче середнього.
4. Коли Стів Янг, захисник, грав у футбол, він важив 205 фунтів. Скільки стандартних відхилень вище або нижче середнього він був?
Того ж року середня вага для Dallas Cowboys становила 240,08 фунтів зі стандартним відхиленням 44,38 фунтів. Емміт Сміт важив у 209 фунтів. Що стосується своєї команди, хто був легше, Сміт чи Янг? Як ви визначили свою відповідь?

Відповідь

174; 177; 178; 184; 185; 185; 185; 185; 190; 200; 205; 205; 206; 210; 210; 212; 212; 215; 220; 223; 228; 232; 241; 241; 242; 245; 250; 250; 259; 260; 265; 265; 270; 272; 275; 276; 278; 280; 285; 285; 286; 290; 290; 295; 302
241
205.5
272.5
205.5, 272.5
зразок
населення
1. 236.34
2. 37.50
3. 161.34
4. 0.84 std. dev. нижче середнього
Молодий

Вправа 2.8.10

Сто викладачів відвідали семінар з розв'язання математичних задач. Ставлення репрезентативної вибірки 12 вчителів вимірювали до і після семінару. Позитивне число для зміни ставлення вказує на те, що ставлення вчителя до математики стало більш позитивним. 12 балів змін такі:

3; 8; —1; 2; 0; 5; —3; 1; —1; 6; 5; -2

Що таке середня оцінка зміни?
Яке стандартне відхилення для цієї популяції?
Що таке показник зміни медіани?
Знайдіть оцінку змін, яка становить 2,2 стандартних відхилень нижче середнього.

Вправа 2.8.11

Зверніться до рис. Визначте, які з наведених нижче є істинними, а які є хибними. Поясніть своє рішення кожній частині у повних реченнях.

Це показує три графіки. Перша - гістограма з режимом 3 і досить симетричним розподілом між 1 (мінімальне значення) і 5 (максимальне значення). Другий графік - гістограма з піками в 1 (мінімальне значення) і 5 (максимальне значення) з 3, що мають найменшу частоту. Третій графік - це квадратний сюжет. Перший вус простягається від 0 до 1. Коробка починається в першій квартилі, 1, і закінчується в третьому квартилі,6. Вертикальна пунктирна лінія позначає медіану на 3. Другий вус тягнеться від 6 на. — Малюнок\(\PageIndex{6}\).

</figure>

Медіани для всіх трьох графіків однакові.
Ми не можемо визначити, чи відрізняється будь-який із засобів для трьох графіків.
Стандартне відхилення для графіка b більше, ніж стандартне відхилення для графіка a.
Ми не можемо визначити, чи відрізняється хтось із третіх квартилів для трьох графіків.

Відповідь

Правда
Правда
Правда
Помилковий

Вправа 2.8.12

У недавньому випуску IEEE Spectrum було оголошено 84 інженерні конференції. Чотири конференції тривали два дні. Тридцять шість тривали три дні. Вісімнадцять тривали чотири дні. Дев'ятнадцять тривали п'ять днів. Чотири тривали шість днів. Один тривав сім днів. Один тривав вісім днів. Один тривав дев'ять днів. Нехай X = довжина (в днях) інженерної конференції.

Організуйте дані в діаграмі.
Знайдіть медіану, перший квартиль і третій квартиль.
Знайдіть ^65-й процентиль.
Знайдіть ^10-й процентиль.
Побудувати квадратний графік даних.
Середні 50% конференцій тривають від _______ днів до _______ днів.
Розрахуйте вибіркове середнє значення днів інженерних конференцій.
Розрахуйте вибірку стандартного відхилення днів інженерних конференцій.
Знайдіть режим.
Якби ви планували інженерну конференцію, яку б ви вибрали як тривалість конференції: середня; медіана; або режим? Поясніть, чому ви зробили цей вибір.
Наведіть дві причини, чому ви думаєте, що три-п'ять днів, здається, популярні довжини інженерних конференцій.

Вправа 2.8.13

Опитування зарахування в 35 громадських коледжів по всій території Сполучених Штатів дало наступні цифри:

6414; 150; 2109; 9350; 21828; 4300; 594; 572; 2825; 2044; 5481; 5200; 5853; 2750; 1012; 6357; 27000; 9414; 7681; 320; 1750; 9200; 7380; 18314; 6557; 13713; 1768; 7493; 71; 2861; 1263; 7285; 28165; 5080; 11622

Організуйте дані в діаграму з п'ятьма інтервалами однакової ширини. Позначте два стовпці «Зарахування» та «Частота».
Побудувати гістограму даних.
Якби ви будували новий коледж громади, яка інформація була б більш цінною: режим чи середнє?
Обчисліть середнє значення зразка.
Обчисліть стандартне відхилення зразка.
Школа із зарахуванням 8000 буде скільки стандартних відхилень від середнього?

Відповідь

Зарахування	Частота
1000-5000	10
5000-10000	16
10000-15000	3
15000-20000	3
20000-25000	1
25000-30000	2

Перевірте рішення студента.
режим
8628.74
6943.88
—0,09

Використовуйте наступну інформацію, щоб відповісти на наступні дві вправи. \(X =\)кількість днів на тиждень, що 100 клієнтів використовують конкретний тренажерний зал.

\(x\)	Частота
\ (x\) ">0	3
\ (x\) ">1	12
\ (x\) ">2	33
\ (x\) ">3	28
\ (x\) ">4	11
\ (x\) ">5	9
\ (x\) ">6	4

Вправа 2.8.14

^80-й процентиль - _____

Вправа 2.8.15

Число, яке на 1,5 стандартних відхилень НИЖЧЕ середнього становить приблизно _____

0.7
4.8
—2.8
Не може бути визначено

Відповідь

Вправа 2.8.16

Припустимо, що видавець провів опитування, запитуючи дорослих споживачів про кількість художніх книг у м'якій обкладинці, які вони придбали за попередній місяць. Результати зведені в табл.

Кількість книг	Фрек.	Рел. Фрек.
0	18
1	24
2	24
3	22
4	15
5	10
7	5
9	1

Чи є якісь викиди в даних? Використовуйте відповідний числовий тест із залученням IQR для виявлення викидів, якщо такі є, та чітко сформулюйте свій висновок.
Якщо значення даних ідентифікується як викид, що з цим слід робити?
Чи є які-небудь значення даних далі двох стандартних відхилень від середнього? У деяких ситуаціях статистики можуть використовувати ці критерії для виявлення значень даних, які є незвичними порівняно з іншими значеннями даних. (Зауважте, що цей критерій є найбільш доцільним для використання для даних, які мають згорнуту форму і симетричність, а не для перекосованих даних.)
Чи дають частини a і c цієї задачі однакову відповідь?
Вивчіть форму даних. Яка частина, a або c, цього питання дає більш відповідний результат для цих даних?
Виходячи з форми даних, яка є найбільш підходящою мірою центру для цих даних: середня, медіана або режим?

Глосарій

Стандартне відхилення: число, яке дорівнює квадратному кореню дисперсії і вимірює, наскільки далекі значення даних від їх середнього; позначення: s для стандартного відхилення вибірки і σ для стандартного відхилення населення.

Автори та атрибуція

дисперсія: середнє квадратичне відхилення від середнього, або квадрат стандартного відхилення; для набору даних відхилення можна представити як \(x\)—\(\bar{x}\) де\(x\) значення даних і\(\bar{x}\) середнє значення вибірки. Дисперсія вибірки дорівнює сумі квадратів відхилень, поділеної на різницю розмірів вибірки і одиниці.

Template:ContribOpenStax