Skip to main content
LibreTexts - Ukrayinska

14.E: Регресія (вправи)

  1. Last updated
  2. Save as PDF
  • Page ID
    98203

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Загальні питання

    Q1

    Що таке рівняння для лінії регресії? До чого відноситься кожен термін у рядку? (відповідний розділ)

    Q2

    Формула рівняння регресії на основі розміру вибірки\(25\) спостережень є\(Y' = 2X + 9\).

    1. Яким був би прогнозований бал для людини, яка забила\(6\) на\(X\)?
    2. Якщо чийсь прогнозований бал був\(14\), на чому була оцінка цієї людини\(X\)? (відповідний розділ)

    Q3

    Який критерій використовується для вирішення того, яка лінія регресії підходить найкраще? (відповідний розділ)

    Q4

    Що означає стандартна похибка кошторисної міри? Яка формула стандартної похибки кошторису? (відповідний розділ)

    Q5

    1. У регресійному аналізі сума квадратів для прогнозованих балів дорівнює\(100\) і сума похибки квадратів -\(200\) що таке\(R^2\)?
    2. В іншому регресійному\(40\%\) аналізі було пояснено дисперсію. Загальна сума квадратів дорівнює\(1000\). Яка сума квадратів передбачуваних значень? (відповідний розділ)

    Q6

    Для\(X,Y\) наведених нижче даних обчислити:

    1. \(r\)і визначити, чи значно він відрізняється від нуля.
    2. нахил лінії регресії і перевірити, чи значно вона відрізняється від нуля.
    3. \(95\%\)довірчий інтервал для ухилу.

    (відповідний розділ)

    X
    Y
    2
    5
    4
    6
    4
    7
    5
    11
    6
    12

    Q7

    Які припущення потрібні для обчислення різної інференційної статистики лінійної регресії? (відповідний розділ)

    Q8

    Співвідношення між роками освіти і зарплатою у вибірці\(20\) людей з певної компанії є\(0.4\). Чи є ця кореляція статистично значущою на\(0.05\) рівні? (відповідний розділ)

    Q9

    Береться вибірка\(X\) і\(Y\) балів, а лінія регресії використовується для прогнозування\(Y\) з\(X\). Якщо\(SSY' = 300\)\(SSE = 500\), і\(N = 50\), що таке: (відповідний розділ відповідного розділу)

    1. \(SSY\)?
    2. стандартна похибка кошторису?
    3. \(R^2\)?

    Q10

    Використовуючи лінійну регресію, знайдіть прогнозований бал після тесту для когось із оцінкою\(43\) на попередньому тесті. (відповідний розділ)

    Попередньо Пост
    59 56
    52 63
    44 55
    51 50
    42 66
    42 48
    41 58
    45 36
    27 13
    63 50
    54 81
    44 56
    50 64
    47 50
    55 63
    49 57
    45 73
    57 63
    46 46
    60 60
    65 47
    64 73
    50 58
    74 85
    59 44

    Q11

    Рівняння для лінії регресії, що прогнозує кількість годин телевізора, переглянутого дітьми (\(Y\)) від кількості годин телевізора, переглянутого їхніми батьками (\(X\)), становить\(Y' = 4 + 1.2X\). Розмір вибірки є\(12\).

    1. Якщо стандартна похибка\(b\) є\(0.4\), чи є схил статистично значущим на\(0.05\) рівні? (відповідний розділ)
    2. Якщо середнє\(X\) значення є\(8\), що означає\(Y\)? (відповідний розділ)

    Q12

    На підставі наведеної нижче таблиці обчислити лінію регресії, яка прогнозує\(Y\) від\(X\). (відповідний розділ)

    MX
    МІЙ
    		 х Си р
    10
    12
    		 2.5 3.0 -0.6

    Q13

    Чи\(B\) є\(A\) або є більша стандартна похибка кошторису? (відповідний розділ)

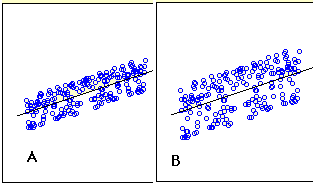
    se_est_graph.gif

    Q14

    True/false: Якщо нахил простої лінії лінійної регресії статистично значущий, то кореляція також завжди буде значною. (відповідний розділ)

    Q15

    True/false: Якщо нахил співвідношення між\(X\) і\(Y\) більше,\(\text{Population 1}\) ніж для\(\text{Population 2}\), кореляція обов'язково буде більшою,\(\text{Population 1}\) ніж в\(\text{Population 1}\). Чому чи чому ні? (відповідний розділ)

    Q16

    True/false: Якщо кореляція є\(0.8\), то\(40\%\) дисперсія пояснюється. (відповідний розділ)

    Q17

    True/false: Якщо фактичний\(Y\) бал був\(31\), але передбачуваний бал був\(28\), то помилка прогнозування є\(3\). (відповідний розділ)

    Питання з тематичних досліджень

    Наступне питання з тематичного дослідження Angry Moods (AM).

    Q18

    (AM #23) Знайдіть лінію регресії для прогнозування Anger-Out з Control-Out.

    1. Що таке ухил?
    2. Що таке перехоплення?
    3. Чи є відносини хоча б приблизно лінійними?
    4. Перевірте, чи значно відрізняється нахил від\(0\).
    5. Яка стандартна похибка кошторису?

    (відповідний розділ, відповідний розділ, відповідний розділ)

    Наступне питання з тематичного дослідження SAT та GPA (SG).

    КВАРТАЛ 19

    (SG #3) Знайдіть лінію регресії для прогнозування загального балу університету від середньої школи GPA.

    1. Що таке ухил?
    2. Що таке\(y\) -перехоплення?
    3. Якщо хтось мав середній\(2.2\) бал у середній школі, яка найкраща оцінка його або її коледжу GPA?
    4. Якщо хтось мав середній\(4.0\) бал у середній школі, яка найкраща оцінка його або її коледжу GPA?

    (відповідний розділ)

    Наступні питання взяті з тематичного дослідження водіння (D).

    Q20

    (D #5) Яка кореляція між віком і як часто людина вирішує їздити в негоду? Чи є ця кореляція статистично значущою на\(0.01\) рівні? Чи люди похилого віку більш-менш схильні повідомляти, що їздять за кермом в негоду? (відповідний розділ, відповідний розділ)

    Q21

    (D #8) Яка кореляція між тим, як часто людина вирішує їздити в негоду та відсотком нещасних випадків, які, на думку людини, відбуваються в негоду? Чи суттєво відрізняється ця кореляція від\(0\)? (відповідний розділ, відповідний розділ)

    Q22

    (D #10) Використовуйте лінійну регресію, щоб передбачити, як часто хтось їздить на громадському транспорті в негоду від того, який відсоток нещасних випадків, на думку людини, відбуваються в негоду. (Пубтран випадково)

    1. Створіть графік розкиду цих даних і додайте лінію регресії.
    2. Що таке ухил?
    3. Що таке перехоплення?
    4. Чи є відносини хоча б приблизно лінійними?
    5. Перевірте, чи значно відрізняється ухил від\(0\).
    6. Прокоментуйте можливі допущення порушень для випробування ухилу.
    7. Яка стандартна похибка кошторису?

    (відповідний розділ, відповідний розділ, відповідний розділ)

    Вибрані відповіді

    S2

    1. \(21\)

    S5

    1. \(0.33\)

    S6

    1. \(b = 1.91\)

    S9

    1. \(800\)

    S12

    \(a = 19.2\)

    S18

    1. \(3.45\)

    S19

    1. \(2.6\)

    S20

    \(r = 0.43\)

    S22

    1. \(0.35\)