14.1: Вступ до лінійної регресії
- Page ID
- 98191
Цілі навчання
- Визначити похибки прогнозування на розсіяному графіку з лінією регресії
У простій лінійній регресії ми прогнозуємо бали по одній змінній з балів на другій змінній. Змінна, яку ми прогнозуємо, називається змінною критерію і називається\(Y\). Змінна, на якій ми базуємо наші прогнози, називається змінною предиктора і називається\(X\). Коли є тільки одна змінна предиктора, метод прогнозування називається простою регресією. У простій лінійній регресії, тема цього розділу, передбачення того,\(Y\) коли побудована як функція\(X\) утворюють пряму лінію.
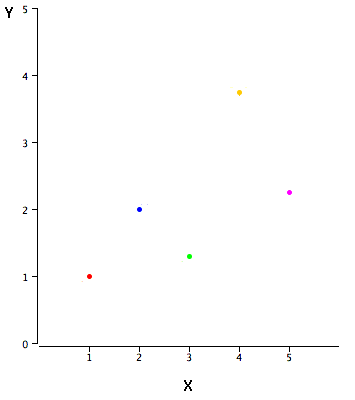
Приклади даних у таблиці\(\PageIndex{1}\) побудовані на рисунку\(\PageIndex{1}\). Можна помітити, що між\(X\) і є позитивний зв'язок\(Y\). Якщо ви збиралися передбачити\(Y\) від\(X\), чим вище значення\(X\), тим вище ваш прогноз\(Y\).
| Х | У |
|---|---|
| 1.00 | 1.00 |
| 2.00 | 2.00 |
| 3.00 | 1.30 |
| 4.00 | 3.75 |
| 5.00 | 2.25 |
Лінійна регресія полягає у знаходженні найбільш підходящої прямої лінії через точки. Найкраще підігнана лінія називається лінією регресії. Чорна діагональна лінія на малюнку\(\PageIndex{2}\) є лінією регресії і складається з прогнозованої\(Y\) оцінки для кожного можливого значення\(X\). Вертикальні лінії від точок до лінії регресії представляють похибки прогнозування. Як бачите, червона точка знаходиться дуже близько лінії регресії; похибка її прогнозування невелика. На відміну від цього, жовта точка набагато вище лінії регресії і тому її похибка прогнозування велика.
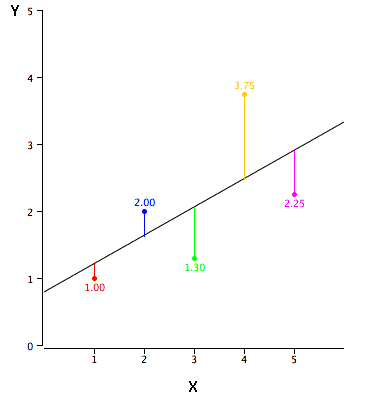
Похибкою прогнозування для точки вважається значення точки мінус прогнозоване значення (значення на прямій). Таблиця\(\PageIndex{2}\) показує прогнозовані значення (\(Y'\)) і похибки прогнозування (\(Y-Y'\)). Наприклад, перша точка має a\(Y\) of\(1.00\) і передбачений\(Y\) (називається\(Y'\)) of\(1.21\). Тому його похибка прогнозування є\(-0.21\).
| Х | У | Y' | Y-Y' | (Y-Y') 2 |
|---|---|---|---|---|
| 1.00 | 1.00 | 1.210 | -0.210 | 0,044 |
| 2.00 | 2.00 | 1,635 | 0,365 | 0.133 |
| 3.00 | 1.30 | 2.060 | -0.760 | 0,578 |
| 4.00 | 3.75 | 2.485 | 1.265 | 1.600 |
| 5.00 | 2.25 | 2.910 | -0.660 | 0,436 |
Можливо, ви помітили, що ми не уточнили, що мається на увазі під «найкращою лінією». На сьогоднішній день найбільш часто використовуваним критерієм для оптимального підгонки лінії є лінія, яка мінімізує суму квадратних похибок прогнозування. Це критерій, який використовувався для пошуку рядка на малюнку\(\PageIndex{2}\). Останній стовпець таблиці\(\PageIndex{2}\) показує квадрат похибки прогнозування. Сума квадратних похибок прогнозування, показаних у таблиці\(\PageIndex{2}\), нижча, ніж для будь-якої іншої лінії регресії.
Формула для лінії регресії
\[Y' = bX + A\]
де\(Y'\) передбачуваний рахунок,\(b\) - нахил лінії, і\(A\) є\(Y\) перехоплення. Рівняння для прямої на\(\PageIndex{2}\) малюнку
\[Y' = 0.425X + 0.785\]
Для\(X = 1\),
\[Y' = (0.425)(1) + 0.785 = 1.21\]
Для\(X = 2\),
\[Y' = (0.425)(2) + 0.785 = 1.64\]
Обчислення лінії регресії
У століття комп'ютерів лінія регресії зазвичай обчислюється статистичним програмним забезпеченням. Однак розрахунки відносно легкі, і наведені тут для всіх, хто цікавиться. Розрахунки проводяться на основі статистики, наведеної в табл\(\PageIndex{3}\). \(M_X\)це середнє значення\(X\),\(M_Y\) є середнім\(Y\),\(s_X\) є стандартним відхиленням\(X\),\(s_Y\) є стандартним відхиленням\(Y\), і\(r\) є кореляцією між\(X\) і\(Y\).
Формула стандартного відхилення
Формула кореляції
| М Х | М У | S X | S Y | р |
|---|---|---|---|---|
| 3 | 2.06 | 1.581 | 1.072 | 0.627 |
Ухил (\(b\)) можна розрахувати наступним чином:
\[b = r \frac{s_Y}{s_X}\]
і перехоплення (\(A\)) можна обчислити як
\[A = M_Y - bM_X\]
Для цих даних,
\[b = \frac{(0.627)(1.072)}{1.581} = 0.425\]
\[A = 2.06 - (0.425)(3) = 0.785\]
Зверніть увагу, що всі розрахунки були показані з точки зору вибіркової статистики, а не параметрів населення. Формули однакові; просто використовуйте значення параметрів для засобів, стандартних відхилень та кореляції.
Стандартизовані змінні
Рівняння регресії простіше, якщо змінні стандартизовані так, щоб їх середні значення дорівнювали\(0\) і стандартні відхилення дорівнювали\(1\), для потім\(b = r\) і\(A = 0\). Це робить лінію регресії:
\[Z_{Y'} = (r)(Z_X)\]
де\(Z_{Y'}\) передбачуваний стандартний бал для\(Y\),\(r\) це кореляція, і\(Z_X\) стандартизований бал для\(X\). Зверніть увагу, що нахил рівняння регресії для стандартизованих змінних є\(r\).
Реальний приклад
Тематичне дослідження «SAT і College GPA» містить середні та університетські оцінки для\(105\) інформатики спеціальностей в місцевій державній школі. Зараз ми розглянемо, як ми могли б передбачити середній бал студента, якби ми знали його середній бал школи.
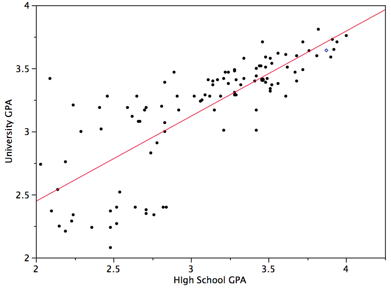
Малюнок\(\PageIndex{3}\) показує розкид графік університетського GPA як функції середньої школи GPA. З малюнка видно, що існує міцна позитивна взаємозв'язок. Кореляція є\(0.78\). Рівняння регресії таке:
\[\text{University GPA'} = (0.675)(\text{High School GPA}) + 1.097\]
Тому студенту з середнім середнім балом школи\(3\) буде передбачено мати університетський бал
\[\text{University GPA'} = (0.675)(3) + 1.097 = 3.12\]
припущення
Це може вас здивувати, але розрахунки, наведені в цьому розділі, не містять припущень. Звичайно, якби відносини між\(X\) і не\(Y\) були лінійними, функція іншої форми могла б краще відповідати даними. Вихідні статистичні дані в регресії ґрунтуються на кількох припущеннях, і ці припущення представлені в більш пізньому розділі цієї глави.
