Skip to main content
LibreTexts - Ukrayinska

12.7: Корельовані пари

  1. Last updated
  2. Save as PDF
  • Page ID
    98060

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Визначте, чи є у вас корельовані пари або незалежні групи
    • Обчислити тест t для корельованих пар

    Розглянемо, як проаналізувати дані з тематичного дослідження «Лікування СДУГ». Ці дані складаються з балів\(24\) дітей із СДУГ за завданням із затримкою задоволення (DOG). Кожна дитина була протестована під чотирма дозовими рівнями. У цьому розділі ми будемо стосуватися лише тестування різниці між середнім станом плацебо (\(D0\)) та середнім умовою найвищої дозування (\(D60\)). Перше питання полягає в тому, чому різницю між засобами не слід перевіряти за допомогою процедури, описаної в розділі Різниця між двома засобами (незалежними групами). Відповідь полягає в тому, що в цьому експерименті у нас немає самостійних груп. Оцінки в\(D0\) умові взяті з тих же предметів, що й бали в\(D60\) умові. Існує лише одна група суб'єктів, кожен предмет тестується як в умовах, так\(D0\) і в\(D60\) умовах.

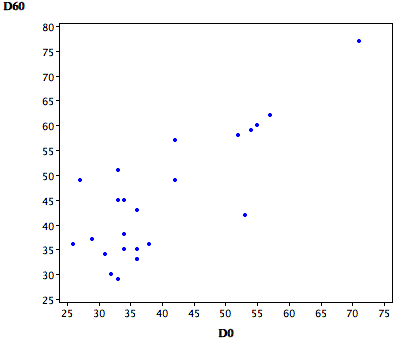
    Малюнок\(\PageIndex{1}\) показує графік розкиду\(60\) -mg балів (\(D60\)) як функція\(0\) -mg балів (\(D0\)). Зрозуміло, що діти, які стають більш правильними в\(D0\) стані, як правило, стають більш правильними в\(D60\) стані. Кореляція між двома умовами висока:\(r = 0.80\). Очевидно, що ці дві змінні не є незалежними.

    d0_d60_corr.gif
    Малюнок\(\PageIndex{1}\): Кількість правильних відповідей, зроблених у стані\(60\) -mg як функція кількості правильних відповідей у стані\(0\) -mg

    Обчислення

    Ви можете згадати, що метод перевірки різниці між цими засобами був представлений в розділі, присвяченому «Тестуванню єдиного середнього». Обчислювальна процедура полягає в тому, щоб обчислити різницю між\(D60\) і\(D0\) умовами для кожної дитини і перевірити, чи суттєво відрізняється середня різниця від\(0\). Показники різниці наведені в табл\(\PageIndex{1}\). Як показано в розділі про тестування єдиного середнього, середня різниця балів,\(4.96\) яка значно відрізняється від\(0\):\(t = 3.22,\; df = 23,\; p = 0.0038\). Цей\(t\) тест має різні назви, включаючи "\(t\)корельований тест" та "\(t\)тест пов'язаних пар».

    Загалом, корельований\(t\) тест обчислюється спочатку обчисленням різниці між двома балами для кожного предмета. Потім на середнє значення цих різницевих балів обчислюється тест єдиного середнього.

    Таблиця\(\PageIndex{1}\): БАЛИ DOG в залежності від дозування
    D0 D60 Д60-Д0
    57 62 5
    27 49 22
    32 30 -2
    31 34 3
    34 38 4
    38 36 -2
    71 77 6
    33 51 18
    34 45 11
    53 42 -11
    36 43 7
    42 57 15
    26 36 10
    52 58 6
    36 35 -1
    55 60 5
    36 33 -3
    42 49 7
    36 33 -3
    54 59 5
    34 35 1
    29 37 8
    33 45 12
    33 29 -4

    Якби ви помилково використовували метод для\(t\) перевірки незалежних груп з цими даними, ви б виявили\(t = 1.42\), що\(df = 46\), і\(p = 0.15\). Тобто різниця між засобами не була б виявлена статистично значущою. Це типовий результат: корельовані\(t\) тести майже завжди мають більшу потужність, ніж\(t\) тести незалежних груп. Це пояснюється тим, що в корелюваних\(t\) тестах кожен бал різниці - це порівняння продуктивності в одному стані з продуктивністю того самого предмета в іншому стані. Це робить кожен суб'єкт «своїм контролем» і утримує відмінності між суб'єктами від вступу в аналіз. Результатом є те, що стандартна похибка різниці між засобами менша в корелюваному\(t\) тесті і, оскільки цей термін знаходиться в знаменнику формули для\(t\), призводить до більшого\(t\).

    Детально про стандартну похибку різниці між засобами (необов'язково)

    Щоб зрозуміти, чому стандартна похибка різниці між засобами менша в корельованому\(t\) тесті, розглянемо дисперсію балів різниці. Як показано в розділі, присвяченому Закону суми дисперсії, дисперсія суми або різниці двох змінних\(X\) і\(Y\) становить:

    \[S_{X\pm Y}^{2} = S_{X}^{2} + S_{Y}^{2} \pm 2rS_XS_Y\]

    Отже, дисперсія різницевих балів - це дисперсія в першій умові (\(X\)) плюс дисперсія у другій умові (\(Y\)) мінус удвічі добуток

    1. кореляція,
    2. стандартне відхилення\(X\), і
    3. стандартне відхилення від\(Y\). Для поточного прикладу\(r = 0.80\) і відхилення і стандартні відхилення наведені в табл\(\PageIndex{2}\).
    Таблиця\(\PageIndex{2}\): Відхилення та стандартні відхилення
    D0 D60 Д60 - Д0
    дисперсія 128.02 151.78 56.82
    Sd 11.31 12.32 7.54

    Дисперсію різницевих балів\(56.82\) можна обчислити як:

    \[128.02 + 151.78 - (2)(0.80)(11.31)(12.32)\]

    яка дорівнює\(56.82\) за винятком похибки округлення. Зверніть увагу, що чим вище кореляція, тим нижче стандартна похибка середнього.