12.5: Попарні порівняння

Last updated
Save as PDF

Page ID: 98059

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте попарне порівняння
Опишіть проблему з\(t\) проведенням тестів серед усіх пар засобів
Обчисліть тест на HSD в Туреччині
Поясніть, чому тест Туреччини не обов'язково повинен вважатися подальшим тестом

Багато експерименти розраховані на порівняння більше двох умов. Ми візьмемо як приклад тематичне дослідження «Посмішки і поблажливість». У цьому дослідженні досліджувався вплив різних типів посмішок на поблажливість, показану людині. Очевидним способом продовжити було б зробити тест на різницю між кожною групою середнього та кожним із засобів іншої групи. Ця процедура призведе до шести порівнянь, показаних у табл\(\PageIndex{1}\).

Таблиця\(\PageIndex{1}\): *Шість порівнянь між засобами*
помилкові проти фетру
помилкові проти жалюгідних
помилковий проти нейтрального
відчував проти нещасних
фетр проти нейтрального
жалюгідний проти нейтрального

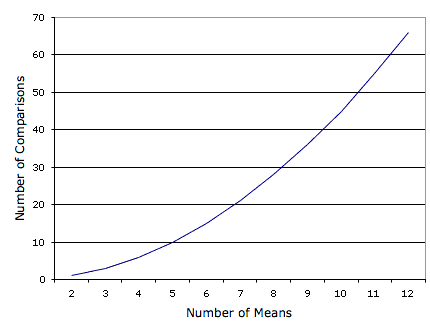
Проблема такого підходу полягає в тому, що якби ви зробили цей аналіз, у вас було б шість шансів зробити помилку типу I. Тому, якщо ви використовували рівень\(0.05\) значущості, ймовірність того, що ви зробите помилку типу I принаймні на одному з цих порівнянь більше, ніж\(0.05\). Чим більше коштів порівнюється, тим більше рівень помилок типу I завищений. \(\PageIndex{1}\)На малюнку показано кількість можливих порівнянь між парами засобів (попарних порівнянь) в залежності від кількості засобів. Якщо коштів всього два, то можна провести тільки одне порівняння. Якщо\(12\) кошти є, то\(66\) можливі порівняння.

Малюнок\(\PageIndex{1}\): Кількість попарних порівнянь як функція кількості засобів

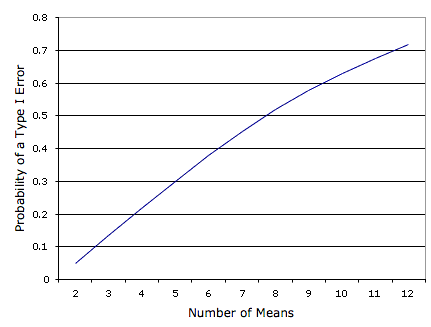
\(\PageIndex{2}\)На малюнку показано ймовірність помилки типу I в залежності від кількості засобів. Як бачите, якщо у вас є експеримент із\(12\) засобами, ймовірність полягає в тому,\(0.70\) що принаймні одне з\(66\) порівнянь між засобами було б значним, навіть якщо всі засоби\(12\) населення були однаковими.

Рисунок\(\PageIndex{2}\): Імовірність помилки **I типу** як функція кількості середніх

Тест на істотну різницю в Туреччині

Частота помилок типу I можна контролювати за допомогою тесту під назвою Тьюкі Чесно Значна різниця тест або Takey HSD для стислості. HSD Туреччини заснований на варіації\(t\) розподілу, яка враховує кількість порівнюваних засобів. Цей розподіл називається вивченим розподілом діапазону.

Повернемося до дослідження поблажливості, щоб побачити, як обчислити тест HSD Туреччини. Ви побачите, що обчислення дуже схожі на обчислення незалежних груп t test. Кроки викладені нижче:

Обчислити середні та дисперсії кожної групи. Вони наведені нижче.

Таблиця\(\PageIndex{2}\): Засоби і відхилення кожної групи
Стан	Середнє	дисперсія
Помилковий	5.37	3.34
Повсть	4.91	2.83
жалюгідний	4.91	2.11
Нейтральний	4.12	2.32

Обчислюйте\(MSE\), що є просто середнім значенням дисперсій. Вона дорівнює\(2.65\).
Обчислити\[Q=\frac{M_i-M_j}{\sqrt{\tfrac{MSE}{n}}}\] для кожної пари засобів, де\(M_i\) одне\(M_j\) середнє, інше середнє, і\(n\) це кількість балів у кожній групі. За цими даними існують\(34\) спостереження на групу. Значення в знаменнику дорівнює\(0.279\).
Обчислюйте\(p\) для кожного порівняння за допомогою калькулятора Studentized Range. Ступінь свободи дорівнює загальному числу спостережень мінус кількість засобів. Для цього експерименту,\(df = 136 - 4 = 132\).

Тести на ці дані наведені в табл\(\PageIndex{2}\).

Таблиця\(\PageIndex{2}\): *Шість попарних порівнянь*
Порівняння	М _и -М _j	Q	р
Помилкові - Повсть	0,46	1.65	0.649
Помилковий - жалюгідний	0,46	1.65	0.649
Помилковий - нейтральний	1,25	4.48	0,010
Повсть - жалюгідний	0.00	0.00	1.000
Повсть - Нейтральний	0.79	2.83	0.193
Нещасний - Нейтральний	0.79	2.83	0.193

Єдине істотне порівняння - між помилковою посмішкою і нейтральною посмішкою.

Незвично отримати результати, які на поверхні здаються парадоксальними. Наприклад, ці результати, здається, вказують на те, що

помилкова посмішка така ж, як і жалюгідна посмішка,
жалюгідна посмішка така ж, як нейтральний контроль, і
помилкова посмішка відрізняється від нейтрального контролю.

Це явне протиріччя уникається, якщо ви обережні, щоб не прийняти нульову гіпотезу, коли ви не можете її відхилити. Виявлення того, що помилкова посмішка істотно не відрізняється від жалюгідної посмішки, не означає, що вони дійсно однакові. Швидше це означає, що немає переконливих доказів того, що вони різні. Точно так само несуттєва різниця між жалюгідною посмішкою і контролем не означає, що вони однакові. Належний висновок полягає в тому, що помилкова посмішка вище, ніж контроль, і що жалюгідна посмішка є або

дорівнює помилковій посмішці,
дорівнює контролю, або
десь посередині.

Припущення тесту Туреччини по суті такі ж, як і для незалежних груп для тестування: нормальність, однорідність дисперсії та незалежні спостереження. Тест досить стійкий до порушень нормальності. Порушення однорідності дисперсії може бути більш проблематичним, ніж у випадку з двома вибірками, оскільки вона\(MSE\) базується на даних з усіх груп. Припущення про незалежність спостережень важливо і не повинно порушуватися.

Комп'ютерний аналіз

Для більшості комп'ютерних програм ви повинні форматувати свої дані так само, як і для незалежних груп для тестування. Єдина відмінність полягає в тому, що якщо у вас є, скажімо, чотири групи, ви б кодували кожну групу як\(1\)\(2\)\(3\), або,\(4\) а не просто\(1\) або\(2\).

Хоча повнофункціональні програми статистики, такі як SAS, SPSS, R та інші, можуть обчислити тест Тукі, менші програми (включаючи Analysis Lab) не можуть. Однак ці програми, як правило, здатні обчислити процедуру, відому як Аналіз дисперсії (ANOVA). Ця процедура буде детально описана в наступному розділі. Його актуальність тут полягає в тому, що ANOVA обчислює\(MSE\) те, що використовується при обчисленні тесту Тукі. Наприклад, нижче показано зведену таблицю ANOVA для даних «Посмішки та поблажливість».

Стовпець з міткою MS розшифровується як «Середній квадрат», і тому значення\(2.6489\) в рядку «Помилка» і стовпці MS є «Середня квадратна помилка» або MSE. Нагадаємо, що це те саме значення, яке обчислюється тут (\(2.65\)) при округленні.

Тест Туреччини не повинен бути подальшим результатом ANOVA

Деякі підручники вводять тест Туреччини лише як подальший аналіз дисперсії. Немає логічної чи статистичної причини, чому ви не повинні використовувати тест Туреччини, навіть якщо ви не обчислюєте ANOVA (або навіть знаєте, що таке). Якщо ви або ваш інструктор не хочете, щоб прийняти наше слово для цього, побачити відмінну статтю з цього та інших питань в статистичному аналізі по Leland Wilkinson і APA Ради наукових справах' Цільова група зі статистичного висновку, опублікований в Американський психолог, Серпень 1999, Vol. № 54, № 8, 594—604.

Обчислення для нерівних розмірів вибірки (необов'язково)

Розрахунок\(MSE\) для нерівних розмірів вибірки аналогічний його розрахунку в незалежних групах t тесту. Ось кроки:

Обчислити помилку Sum of Squares (\(SSE\)), використовуючи наступну формулу,\[SSE=\sum (X-M_1)^2+\sum (X-M_2)^2+\cdots +\sum (X-M_k)^2\] де\(M_i\) середнє\(k\) значення\(i^{th}\) групи і кількість груп.
Обчислити ступінь похибки свободи (\(dfe)\)шляхом віднімання кількості груп (\(k\)) із загальної кількості спостережень (\(N\)). Тому,\[dfe = N - k\]
Обчислення\(MSE\)\(SSE\) шляхом ділення на\(dfe\):\[MSE = \frac{SSE}{dfe}\]
Для кожного порівняння засобів використовуйте гармонійне середнє значення\(n's\) для двох засобів (\(\mathfrak{n_h}\)).

Всі інші аспекти розрахунків такі ж, як при рівних розмірах вибірки.