12.1: Тестування єдиного середнього
- Page ID
- 98035
Цілі навчання
- Обчислити ймовірність того, що середнє значення вибірки буде принаймні таким же високим, як вказане значення\(\sigma\), коли відомо
- Обчислення двоххвостової ймовірності
- Обчислити ймовірність того, що середнє значення вибірки буде принаймні таким же високим, як задане значення, коли\(\sigma\) оцінюється
- Викладіть припущення, необхідні для пункту\(3\) вище
У цьому розділі показано, як перевірити нульову гіпотезу про те, що середнє значення популяції дорівнює деякому гіпотезованому значенню. Наприклад, припустимо, що експериментатор хотів дізнатися, чи на людей впливає підсвідоме повідомлення, і виконав наступний експеримент. Кожен з дев'яти предметів представлений серією\(100\) пар картинок. У міру подання пари картинок подається підсвідоме повідомлення, яке передбачає картину, яку повинен вибрати суб'єкт. Питання в тому, чи дорівнює (популяція) середня кількість разів обраної запропонованої картини\(50\). Іншими словами, нульова гіпотеза полягає в тому, що популяція mean (\(\mu\)) є\(50\). (Гіпотетичні) дані наведені в табл\(\PageIndex{1}\). Дані в таблиці\(\PageIndex{1}\) мають зразок середнього значення (\(M\))\(51\). Таким чином, середнє значення вибірки відрізняється від гіпотезованої популяції на середнє значення\(1\).
| Частота |
|---|
| 45 |
| 48 |
| 49 |
| 49 |
| 51 |
| 52 |
| 53 |
| 55 |
| 57 |
Тест на значущість складається з обчислення ймовірності середнього зразка, що\(\mu\) відрізняється від одиниці (різниця між гіпотезованим середнім показником популяції та середнім вибірковим) або більше. Насамперед необхідно визначити розподіл вибірки середнього. Як показано в попередньому розділі, середнє і стандартне відхилення розподілу вибірки середнього
\[μ_M = μ\]
і
\[\sigma_M = \dfrac{\sigma}{\sqrt{N}}\]
відповідно. Зрозуміло, що\(\mu _M=50\). Для того, щоб обчислити стандартне відхилення розподілу вибірки середнього, ми повинні знати стандартне відхилення популяції (\(\sigma\)).
Поточний приклад був побудований як один з небагатьох випадків, в яких стандартне відхилення відомо. На практиці дуже малоймовірно, що ви б знали\(\sigma\) і тому використовували б\(s\), зразок кошторису\(\sigma\). Однак повчально побачити, як обчислюється ймовірність, якщо вона\(\sigma\) відома, перш ніж приступити до того, як вона обчислюється, коли\(\sigma\) оцінюється.
Для поточного прикладу, якщо нульова гіпотеза істинна, то на основі біноміального розподілу можна обчислити, що дисперсія числа correct дорівнює
\[\sigma ^2 = N\pi (1-\pi ) = 100(0.5)(1-0.5) = 25\]
Тому,\(\sigma =5\). Для a\(\sigma \) of\(5\) і an\(N\) of\(9\) стандартне відхилення розподілу вибірки середнього значення дорівнює\(5/3 = 1.667\). Нагадаємо, що стандартне відхилення розподілу вибірки називається стандартною похибкою.
Нагадаємо, ми хочемо знати ймовірність отримання зразка середнього\(51\) або більше, коли розподіл вибірки середнього значення має середнє значення\(50\) і стандартне відхилення\(1.667\). Для обчислення цієї ймовірності зробимо припущення, що розподіл вибірки середнього нормально розподілений. Потім ми можемо використовувати нормальний калькулятор розподілу, як показано на малюнку\(\PageIndex{1}\).
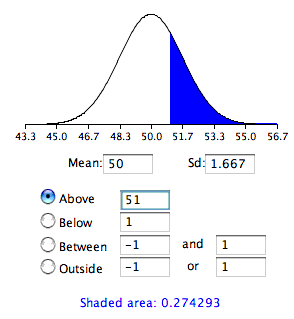
Зверніть увагу, що середнє значення встановлено\(50\), стандартне відхилення до\(1.667\), а область вище\(51\) запитується і показана\(0.274\).
Тому ймовірність отримання зразка середнього\(51\) або більшого дорівнює\(0.274\). Оскільки середнє\(51\) або вище не є малоймовірним за припущенням, що підсвідоме повідомлення не має ефекту, ефект не є значним, а нульова гіпотеза не відхиляється.
Тест, проведений вище, був однохвостим тестом, оскільки він обчислив ймовірність того, що середнє значення зразка буде на одну або кілька балів вище, ніж гіпотезоване середнє значення,\(50\) а обчислена площа була площею вище\(51\). Щоб перевірити двоххвосту гіпотезу, ви б обчислили ймовірність вибіркового середнього значення, що відрізняється на один або кілька в будь-якому напрямку від гіпотезованого середнього\(50\). Ви б зробили це, обчисливши ймовірність того, що середнє значення менше\(49\) або дорівнює або більше або дорівнює\(51\).
Результати калькулятора нормального розподілу наведені на малюнку\(\PageIndex{2}\).
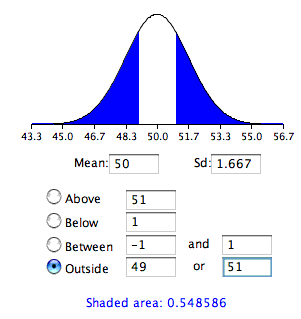
Як бачите, ймовірність така,\(0.548\) яка, як і очікувалося, вдвічі перевищує ймовірність\(0.274\) показаної на малюнку\(\PageIndex{1}\).
Перш ніж звичайні калькулятори, такі як ілюстрований вище, були широко доступні, обчислення ймовірності проводилися на основі стандартного нормального розподілу. Це було зроблено шляхом обчислень на\(Z\) основі формули
\[Z=\frac{M-\mu }{\sigma _M}\]
де\(Z\) - значення на стандартному нормальному розподілі,\(M\) є вибірковим\(\mu\) середнім, є гіпотезованим значенням середнього, і\(\sigma _M\) є стандартною похибкою середнього. Для цього прикладу,\(Z = (51-50)/1.667 = 0.60\). Використовуйте звичайний калькулятор, із середнім значенням\(0\) і стандартним відхиленням\(1\), як показано нижче.
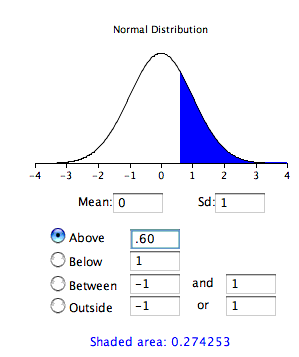
Зверніть увагу, що ймовірність (затінена область) така ж, як і раніше розрахована (для однохвостого тесту).
Як зазначалося, в реальному світі аналізу даних дуже рідко, що ви б знали\(\sigma\) і хотіли б оцінити\(\mu\). Як правило\(\sigma\), невідомо і оцінюється у вибірці по\(s\), і\(\sigma _M\) оцінюється по\(s_M\).
Приклад\(\PageIndex{1}\): adhd treatment
C Розглянемо дані в тематичному дослідженні «Лікування СДУГ». Ці дані складаються з балів\(24\) дітей із СДУГ за завданням із затримкою задоволення (DOG). Кожна дитина була протестована під чотирма дозовими рівнями. У таблиці\(\PageIndex{2}\) наведені дані для плацебо (\(0\)мг) і найвищого рівня дозування (\(0.6\)мг) метилфенідату. Особливий інтерес тут представляє колонка з маркуванням «Diff», яка показує різницю в продуктивності між\(0.6\) mg (\(D60\)) і\(0\) mg (\(D0\)) conditions. These difference scores are positive for children who performed better in the \(0.6\)mg) умовою, ніж в контрольному стані і негативним для тих хто забив краще в контрольному стані. Якщо метилфенідат надає позитивний ефект, то середній показник різниці в популяції буде позитивним. Нульова гіпотеза полягає в тому, що середня оцінка різниці в популяції є\(0\).
Таблиця\(\PageIndex{2}\): БАЛИ DOG в залежності від дозування
| D0 | D60 | Diff |
|---|---|---|
| 57 | 62 | 5 |
| 27 | 49 | 22 |
| 32 | 30 | -2 |
| 31 | 34 | 3 |
| 34 | 38 | 4 |
| 38 | 36 | -2 |
| 71 | 77 | 6 |
| 33 | 51 | 18 |
| 34 | 45 | 11 |
| 53 | 42 | -11 |
| 36 | 43 | 7 |
| 42 | 57 | 15 |
| 26 | 36 | 10 |
| 52 | 58 | 6 |
| 36 | 35 | -1 |
| 55 | 60 | 5 |
| 36 | 33 | -3 |
| 42 | 49 | 7 |
| 36 | 33 | -3 |
| 54 | 59 | 5 |
| 34 | 35 | 1 |
| 29 | 37 | 8 |
| 33 | 45 | 12 |
| 33 | 29 | -4 |
Рішення
Щоб перевірити цю нульову гіпотезу, ми обчислюємо\(t\) using a special case of the following formula:
\[t=\frac{\text{statistic-hypothesized value}}{\text{estimated standard error of the statistic}}\]
Окремим випадком цієї формули, що застосовується для тестування єдиного середнього, є
\[t=\frac{M-\mu }{s_M}\]
де\(t\) is the value we compute for the significance test, \(M\) is the sample mean, \(\mu\) - гіпотезована величина середнього значення популяції, і\(s_M\) - розрахункова стандартна похибка середнього. Зверніть увагу на схожість цієї формули з формулою для Z.
У попередньому прикладі ми припустили, що бали були нормально розподілені. У цьому випадку саме населення різницевих балів ми вважаємо нормальним розподіленим.
Середнє (\(M\)) of the \(N = 24\) difference scores is \(4.958\), the hypothesized value of \(\mu\)є\(0\), and the standard deviation (\(s\)) is \(7.538\). The estimate of the standard error of the mean is computed as:
\[s_M=\frac{s}{\sqrt{N}}=\frac{7.5382}{\sqrt{24}}=1.54\]
Тому
\[t =\frac{4.96}{1.54} = 3.22\]
Значення ймовірності для калькулятора розподілу\(t\) depends on the degrees of freedom. The number of degrees of freedom is equal to \(N - 1 = 23\). As shown below, the t виявляє, що ймовірність a\(t\) less than \(-3.22\) or greater than \(3.22\) is only \(0.0038\). Therefore, if the drug had no effect, the probability of finding a difference between means as large or larger (in either direction) than the difference found is very low. Therefore the null hypothesis that the population mean difference score is zero can be rejected. The conclusion is that the population mean for the drug condition is higher than the population mean for the placebo condition.
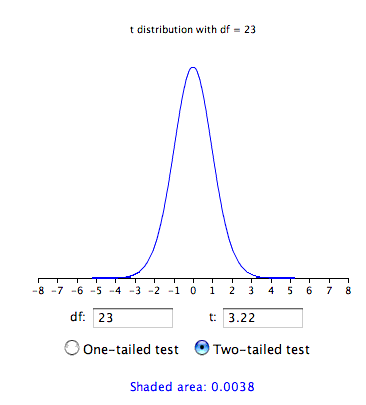
Огляд припущень
- Кожне значення відбирається незалежно один від одного значення.
- Значення відбираються з нормального розподілу.
