9.6: Різниця між засобами
- Page ID
- 98371
Цілі навчання
- Створити середнє значення і дисперсію розподілу вибірки різниці між засобами
- Обчислити стандартну похибку різниці між засобами
- Обчислити ймовірність різниці між засобами, що перевищують задане значення
Статистичні аналізи дуже часто стосуються різниці між засобами. Типовим прикладом є експеримент, покликаний порівняти середнє значення контрольної групи із середнім показником експериментальної групи. Інференційна статистика, яка використовується при аналізі даного виду експерименту, залежить від розподілу вибірки різниці між засобами.
Розподіл вибірки різниці між засобами можна розглядати як розподіл, який буде результатом, якщо ми повторюємо наступні три кроки знову і знову:
- \(n_1\)вибіркові бали від\(\text {Population 1}\) і\(n_2\) бали від\(\text {Population 2}\)
- обчислити засоби двох зразків (\(M_1\)і\(M_2\))
- обчислити різницю між засобами,\(M_1-M_2\)
Розподіл відмінностей між засобами - це розподіл вибірки різниці між засобами.
Як і слід було очікувати, середнє значення розподілу вибірки різниці між засобами становить:
\[\mu _{M_1-M_2}=\mu _1-\mu _2\]
що говорить про те, що середнє значення розподілу відмінностей між вибірковими засобами дорівнює різниці між засобами населення. Наприклад, скажіть, що середній тестовий бал всіх\(12\) -річних дітей у популяції є\(34\) і середнє значення\(10\) -річних є\(25\). Якби численні зразки були взяті з кожної вікової групи і середня різниця обчислюється кожен раз, середнє значення цих численних відмінностей між вибірковими засобами було б\(34-25=9\).
З закону дисперсійної суми ми знаємо, що:
\[\sigma _{M_1-M_2}^{2}=\sigma _{M_1}^{2}+\sigma _{M_2}^{2}\]
що говорить про те, що дисперсія розподілу вибірки різниці між засобами дорівнює дисперсії розподілу вибірки середнього для\(\text {Population 1}\) плюс дисперсія розподілу вибірки середнього для\(\text {Population 2}\). Згадаймо формулу для дисперсії розподілу вибірки середнього:
\[\sigma _{M}^{2}=\frac{\sigma ^2}{N}\]
Оскільки ми маємо дві популяції та два розміри зразків, нам потрібно розрізняти дві дисперсії та розміри вибірки. Робимо це за допомогою індексів\(1\) і\(2\). Використовуючи цю умовність, ми можемо написати формулу дисперсії розподілу вибірки різниці між засобами як:
\[\sigma _{M_1-M_2}^{2}=\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}\]
Оскільки стандартна похибка розподілу вибірки є стандартним відхиленням розподілу вибірки, стандартна похибка різниці між засобами становить:
\[\sigma _{M_1-M_2}=\sqrt{\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}}\]
Просто для перегляду позначення символ зліва містить сигму (\(\sigma\)), що означає, що це стандартне відхилення. Індекси\(M_1-M_2\) вказують на те, що це стандартне відхилення розподілу вибірки\(M_1-M_2\).
Тепер давайте розглянемо застосування цієї формули.
Приклад\(\PageIndex{1}\)
Припустимо, що на Марсі є два види зелених істот. Середня висота\(\text{Species 1}\) є в\(32\) той час як середня висота\(\text{Species 2}\) є\(22\). Розбіжності двох видів є\(60\) і\(70\), відповідно, і висоти обох видів зазвичай розподілені. Ви випадковим чином вибірки\(10\)\(14\) членів\(\text{Species 1}\) і членів\(\text{Species 2}\). Яка ймовірність того, що середнє значення\(10\) членів\(\text{Species 1}\) волі перевищить середнє значення\(14\) членів\(\text{Species 2}\) на\(5\) або більше? Не роблячи ніяких розрахунків, ви, напевно, знаєте, що ймовірність досить висока, оскільки різниця в чисельності населення означає\(10\). Але яка саме ймовірність?
Рішення
Для початку визначимося з розподілом вибірки різниці між засобами. Використовуючи наведені вище формули, середнє значення
\[\mu _{M_1-M_2}=32-22=10\]
Стандартна помилка:
\[\sigma _{M_1-M_2}=\sqrt{\frac{60}{10}+\frac{70}{14}}=3.317\]
Розподіл вибірки наведено на малюнку\(\PageIndex{1}\). Зверніть увагу, що він зазвичай розподіляється із середнім значенням\(10\) і стандартним відхиленням\(3.317\). Область вище\(5\) затінена синім кольором.
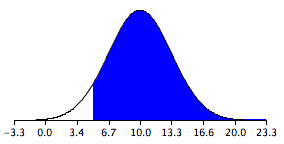
Останній крок - визначити область, яка затінена синім кольором. Використовуючи або\(Z\) таблицю, або звичайний калькулятор, площа може бути визначена\(0.934\). Таким чином, ймовірність того, що середнє значення зразка з\(\text{Species 1}\) перевищить середнє значення зразка з\(\text{Species 2}\) на\(5\) або більше, є\(0.934\).
Як показано нижче, формула стандартної похибки різниці між засобами набагато простіше, якщо розміри вибірки і відхилення населення рівні. Коли відхилення та розміри зразків однакові, немає необхідності використовувати індекси\(1\) та\(2\) диференціювати ці терміни.
\[\sigma _{M_1-M_2}=\sqrt{\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}}=\sqrt{\frac{\sigma ^2}{n}+\frac{\sigma ^2}{n}}=\sqrt{\frac{2\sigma ^2}{n}}\]
Цей спрощений варіант формули може бути використаний для наступної задачі.
Приклад\(\PageIndex{2}\)
Середній зріст\(15\) -річних хлопчиків (в см) є\(175\) і дисперсія становить\(64\). Для дівчат середнє значення є\(165\) і дисперсія є\(64\). Якби були відібрані вісім хлопчиків і вісім дівчаток, яка ймовірність того, що середній зріст вибірки дівчаток був би вище середнього зросту вибірки хлопчиків? Іншими словами, яка ймовірність того, що середній зріст дівчаток мінус середній зріст хлопчиків більше\(0\)?
Рішення
Як і раніше, проблему можна вирішити в плані вибірки розподілу різниці між засобами (дівчатка - хлопчики). Середнє значення розподілу становить 165 - 175 = -10. Стандартне відхилення розподілу становить:
\[\sigma _{M_1-M_2}=\sqrt{\frac{2\sigma ^2}{n}}=\sqrt{\frac{(2)(64)}{8}}=4\]
Графік розподілу показаний на рис\(\PageIndex{2}\). Зрозуміло, що малоймовірно, що середній зріст для дівчаток буде вище середнього зросту для хлопчиків, оскільки в популяції хлопчики зовсім трохи вище. Тим не менш, не немислимо, що середнє значення для дівчат може бути вище, ніж середнє значення для хлопчиків.
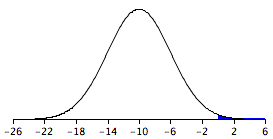
Різниця між засобами 0 і вище - це різниця\(10/4 = 2.5\) стандартних відхилень вище середнього значення\(-10\). Імовірність оцінки\(2.5\) або більш стандартних відхилень вище середнього дорівнює\(0.0062\).
