8.1: Q-Q ділянки
- Page ID
- 98112
Цілі навчання
- Створіть, для яких\(q-q\) ділянок використовуються.
- Опишіть форму\(q-q\) ділянки при дотриманні розподільного припущення.
- Вміти створити нормальний\(q-q\) сюжет.
Квантіль або\(q-q\) графік - це дослідницький графічний пристрій, який використовується для перевірки дійсності розподільного припущення для набору даних. Загалом, основна ідея полягає в обчисленні теоретично очікуваного значення для кожної точки даних на основі розглянутого розподілу. Якщо дані дійсно йдуть за передбачуваним розподілом, то точки на\(q-q\) ділянці будуть падати приблизно на пряму.
Перш ніж заглиблюватися в подробиці\(q-q\) графіків, ми спочатку опишемо два пов'язаних графічних методу оцінки розподільних припущень: гістограму і функцію кумулятивного розподілу (CDF). Як буде видно,\(q-q\) сюжети більш загальні, ніж ці альтернативи.
Оцінка розподільних припущень
Як приклад розглянемо дані, виміряні з фізичного пристрою, такого як вертушка, зображена на малюнку\(\PageIndex{1}\). Червона стрілка обертається навколо центру, а коли стрілка перестає обертатися,\(1\) записується число між\(0\) і. Чи можемо ми визначити, чи справедливий спиннер?
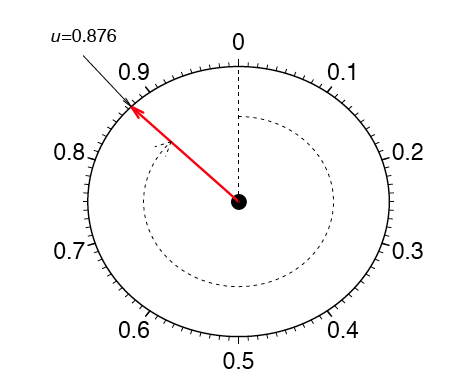
Якщо вертушка справедлива, то ці цифри повинні слідувати рівномірному розподілу. Щоб дослідити, чи є вертушка справедливим, оберніть стрілку\(n\) раз, і запишіть вимірювання по\({\mu _1, \mu _2, ..., \mu _n}\). У цьому прикладі ми збираємо\(n = 100\) зразки. Гістограма забезпечує корисну візуалізацію цих даних. На малюнку\(\PageIndex{2}\) ми показуємо три різні гістограми за шкалою ймовірності. Гістограма повинна бути плоскою для рівномірного зразка, але візуальне сприйняття змінюється залежно від того, чи є гістограма\(10\)\(5\), або\(3\) контейнери. Остання гістограма виглядає плоскою, але дві інші гістограми явно не плоскі. Незрозуміло, на якій гістограмі ми повинні спиратися на свій висновок.
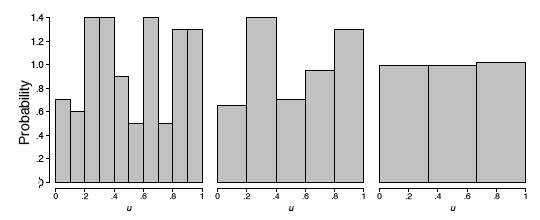
Крім того, ми можемо використовувати функцію кумулятивного розподілу (CDF), яка позначається символом\(F(\mu )\). CDF дає ймовірність того, що спиннер дає значення менше або рівне, тобто ймовірність того\(\mu\), що червона стрілка приземлиться в проміжку\([0, \mu ]\). За допомогою простої арифметики\(F(\mu ) = \mu\), яка представляє собою діагональну пряму лінію\(y = x\). CDF на основі даних вибірки називається емпіричним CDF (ECDF)\(\widehat{F}_n(u)\), позначається і визначається як частка даних менше або дорівнює\(\mu\); тобто
\[\widehat{F}_n(u)=\frac{\#u_i\leq u}{n}\]
Загалом, ECDF набуває рваний сходовий вигляд.
Для зразка вертушки, проаналізованого на малюнку\(\PageIndex{2}\), ми обчислили ECDF і CDF, які відображаються на малюнку\(\PageIndex{3}\). У лівому кадрі ECDF з'являється близько до лінії\(y = x\), показаної в середньому кадрі. У правій рамці ми накладаємо ці дві криві і перевіряємо, що вони дійсно досить близько один до одного. Зверніть увагу, що нам не потрібно вказувати кількість бункерів, як при гістограмі.
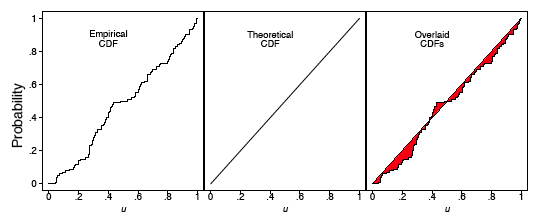
q-q графік для рівномірних даних
Графік\(q-q\) для рівномірних даних дуже схожий на емпіричну графіку CDF, за винятком перевернутих осей. \(q-q\)Сюжет забезпечує наочне порівняння квантилей вибірки з відповідними теоретичними квантилями. Взагалі, якщо точки на\(q-q\) ділянці відходять від прямої, то передбачуваний розподіл ставиться під сумнів.
Тут ми визначаємо q-ю квантиль партії з n чисел як число,\(ξ_q\) таке, що дріб q x n зразка менше\(ξ_q\), тоді як\((1 - q) \times n\) частка зразка більше\(ξ_q\). Найвідомішим квантилем є медіана\(ξ_{0.5}\), яка розташовується посередині вибірки.
Розглянемо невеликий зразок\(5\) чисел від спиннера:
\[\mu _1 = 0.41,\; \mu _2 =0.24,\; \mu _3 =0.59,\; \mu _4 =0.03,\; \mu _5 =0.67\]
Виходячи з нашого опису вертушки, ми очікуємо рівномірного розподілу для моделювання цих даних. Якби вибіркові дані були «ідеальними», то в середньому було б спостереження посередині кожного з\(5\) інтервалів:\(0\)\(0.2\)\(0.2\) to\(0.4\),\(0.4\) to\(0.6\), to і так далі. Таблиця\(\PageIndex{1}\) показує точки\(5\) даних (відсортовані за зростанням) і теоретично очікуване значення кожної з них виходячи з припущення, що розподіл рівномірний (середина інтервалу).
| Дані (μ) | Ранг (i) | Середина в інтервалі |
|---|---|---|
| 0,03 | 1 | 0.1 |
| 0,24 | 2 | 0.3 |
| 0,41 | 3 | 0.5 |
| 0,59 | 4 | 0.7 |
| 0,67 | 5 | 0.9 |
Теоретичні та емпіричні CDF показані на малюнку,\(\PageIndex{4}\) а\(q-q\) графік показаний у лівій рамці рисунка\(\PageIndex{5}\).
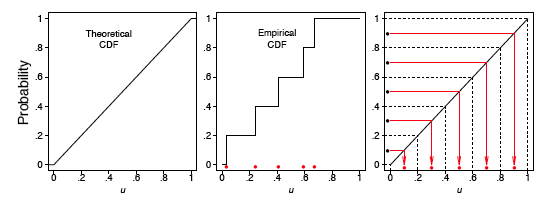
Загалом, повний набір квантилей вибірки ми вважаємо відсортованими значеннями даних
\[μ_{(1)} < μ_{(2)} < μ_{(3)} < \ldots < μ_{(n-1)} < μ_{(n)} ,\]
де дужки в індексі вказують на те, що дані були впорядковані. Грубо кажучи, ми очікуємо, що перше впорядковане значення буде в середині інтервалу\((0, 1/n)\), друге - в середині інтервалу\((1/n, 2/n)\), а останнє - в середині інтервалу\((\tfrac{n - 1}{n}, 1)\). Таким чином, візьмемо за теоретичний квантиль значення
\[\xi _q=q\approx \frac{i-0.5}{n}\]
де\(q\) відповідає\(i^{th}\) впорядкованому значенню вибірки. Віднімаємо кількість\(0.5\) так, щоб опинилися рівно посередині інтервалу\((\tfrac{i-1}{n}, \tfrac{i}{n})\). Ці ідеї зображені в правій рамці малюнка\(\PageIndex{4}\) для нашого невеликого зразка розміру\(n = 5\).
Тепер ми готові точно визначитися з\(q-q\) сюжетом. Спочатку ми обчислюємо n очікуваних значень даних, які ми поєднуємо з n точок даних, відсортованих у порядку зростання. Для рівномірної щільності\(q-q\) ділянку складається з\(n\) впорядкованих пар
\[(\tfrac{i-0.5}{n}, u_i),\; for\; i=1,2,\cdots ,n\]
Це визначення трохи відрізняється від ECDF, яке включає в себе пункти\((u_i, \tfrac{i}{n})\). У лівій рамці\(\PageIndex{5}\) малюнка виводимо\(q-q\) графік\(5\) точок в табл\(\PageIndex{1}\). У правих двох кадрах Figure\(\PageIndex{5}\) ми виводимо\(q-q\) графік тієї ж партії чисел, що використовується на малюнку\(\PageIndex{2}\). У кінцевому кадрі складаємо діагональну лінію\(y = x\) як точку відліку.
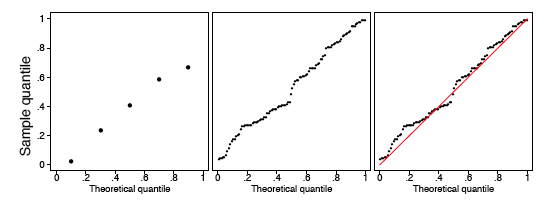
Розмір вибірки слід враховувати, судячи про те, наскільки близький\(q-q\) ділянку до прямої. Ми показуємо два інших рівномірних зразка розміру\(n = 10\) і\(n = 1000\) на малюнку\(\PageIndex{6}\). Зверніть увагу, що\(q-q\) сюжет коли\(n = 1000\) практично ідентичний лінії\(y = x\), тоді як такий не той випадок, коли розмір вибірки є тільки\(n = 10\).
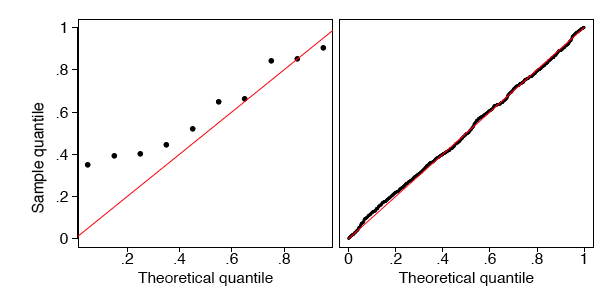
На малюнку\(\PageIndex{7}\) ми показуємо\(q-q\) графіки двох випадкових зразків, які не є однорідними. В обох прикладах квантилі вибірки відповідають теоретичним квантилям лише на медіані та в крайніх точках. Обидва зразки здаються симетричними навколо медіани. Але дані в лівому кадрі ближче до медіани, ніж очікувалося б, якби дані були рівномірними. Дані в правій рамці знаходяться далі від медіани, ніж можна було б очікувати, якби дані були рівномірними.
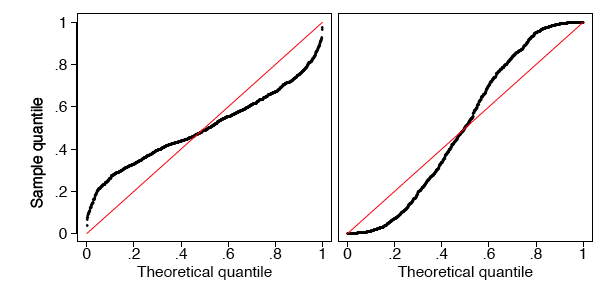
Фактично дані генерувалися\(R\) мовою з бета-дистрибутивів з параметрами\(a = b = 3\)\(a = b =0.4\) зліва і справа. На малюнку\(\PageIndex{8}\) ми показуємо гістограми цих двох наборів даних, які служать для уточнення істинних форм щільностей. Вони явно неоднорідні.
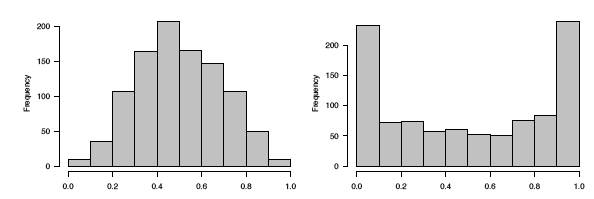
q-q графік для нормальних даних
Визначення\(q-q\) ділянки може бути розширено на будь-яку суцільну щільність. \(q-q\)Ділянка буде близький до прямої, якщо передбачувана щільність правильна. Оскільки кумулятивна функція розподілу рівномірної щільності була прямою лінією,\(q-q\) графік було дуже легко побудувати. Для даних, які не є однорідними, теоретичні квантилі повинні обчислюватися іншим способом.
Нехай\({z_1, z_2, ..., z_n}\) позначають випадкову вибірку з нормального розподілу із середнім\(\mu =0\) і стандартним відхиленням\(\sigma =1\). Нехай впорядковані значення позначаються
\[z_{(1)} < z_{(2)} < z_{(3)} < \ldots < z_{(n-1)} <z_{(n)}\]
Ці n впорядкованих значень гратимуть роль квантилей вибірки.
Розглянемо зразок\(5\) значень з розподілу, щоб побачити, як вони порівнюються з тим, що очікувалося б при нормальному розподілі. \(5\)Значення у порядку зростання показані в першому стовпці таблиці\(\PageIndex{2}\).
| Дані (z) | Ранг (i) | Середина в інтервалі | Звичайний (z) |
|---|---|---|---|
| -1.96 | 1 | 0.1 | -1.28 |
| -0.78 | 2 | 0.3 | -0.52 |
| 0,31 | 3 | 0.5 | 0.00 |
| 1.15 | 4 | 0.7 | 0,52 |
| 1.62 | 5 | 0.9 | 1.28 |
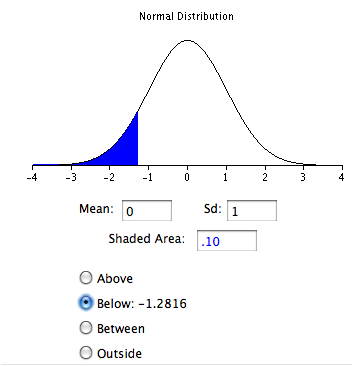
Так само, як і у випадку з рівномірним розподілом, у нас є\(5\) інтервали. Однак при нормальному розподілі теоретичний квантиль - це не середина інтервалу, а навпаки нормального розподілу для середини інтервалу. Беручи перший інтервал як приклад, ми хочемо знати таке\(z\)\(0.1\) значення, що площі в нормальному розподілі нижче\(z\). Це можна обчислити за допомогою зворотного нормального калькулятора, як показано на малюнку\(\PageIndex{9}\). Просто встановіть поле «Shaded Area» на середину інтервалу (\(0.1\)) і натисніть на кнопку «Нижче». Результат є\(-1.28\). Тому\(10\%\) розподіл нижче\(z\) значення\(-1.28\).
\(q-q\)Графік для даних у таблиці\(\PageIndex{2}\) показаний в лівому кадрі рисунка\(\PageIndex{11}\).
Загалом, що ми повинні прийняти як відповідні теоретичні квантилі? Нехай кумулятивна функція розподілу нормальної щільності позначається значенням\(\Phi (z)\). У попередньому прикладі\(\Phi (-1.28)=0.10\) і\(\Phi (0.00)=0.50\). Використовуючи квантильні позначення,\(\xi _q\) якщо\(q^{th}\) квантиль нормального розподілу, то
\[Φ(ξ_q)= q\]
Тобто ймовірність нормальної вибірки менше, ніж\(\xi _q\) насправді просто\(q\).
Розглянемо перше впорядковане значення,\(z_1\). Що ми можемо очікувати, що значення\(\Phi (z_1)\) буде? Інтуїтивно ми очікуємо, що ця ймовірність прийме значення в інтервалі\((0, 1/n)\). Так само ми очікуємо\(\Phi (z_2)\) взяти на себе значення в інтервалі\((1/n, 2/n)\). Продовжуючи, ми\(\Phi (z_n)\) очікуємо падіння в інтервалі\(((n - 1)/n, 1)\). Таким чином, теоретичний квантиль, який ми бажаємо, визначається зворотним (не зворотним) нормальним CDF. Зокрема, теоретичний квантиль, відповідний емпіричному квантілі,\(z_i\) повинен бути
\[ξ_q \approx \dfrac{i-0.5}{n}\]
для\(i = 1, 2, \ldots, n\).
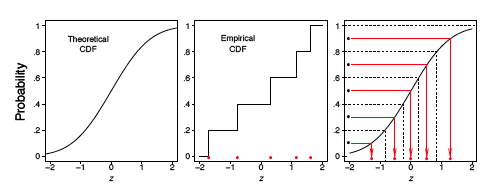
Емпірична CDF та теоретична квантильна побудова для невеликої вибірки, наведеної в таблиці\(\PageIndex{2}\), відображені на рисунку\(\PageIndex{10}\). Для більшої\(100\) вибірки розміру перші кілька очікуваних квантилей є\(-2.576\)\(-2.170\), і\(-1.960\).
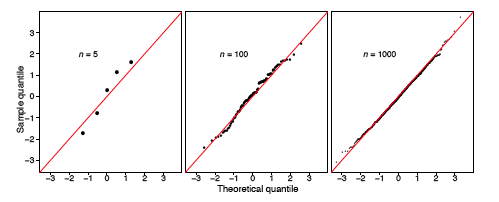
У лівій рамці рисунка ми виводимо графік невеликого нормального зразка\(\PageIndex{11}\), наведеного в табл\(\PageIndex{2}\).\(q-q\) Решта кадрів на малюнку\(\PageIndex{11}\) відображають\(q-q\) графіки звичайних випадкових зразків розміру\(n = 100\) і\(n = 1000\). У міру збільшення розміру вибірки точки на\(q-q\) ділянках лежать ближче до лінії\(y = x\).
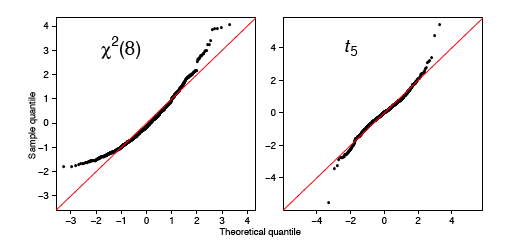
Як і раніше, нормальний\(q-q\) сюжет може свідчити про відступи від нормальності. Два найпоширеніших приклади - це перекошені дані та дані з важкими хвостами (великий куртоз). На малюнку\(\PageIndex{12}\) ми показуємо\(q-q\) нормальні графіки для набору даних з чі-квадратом (перекосом) та набору даних Student's-\(t\) (kurtotic), обидва розміру\(n = 1000\). Дані були вперше стандартизовані. Червона лінія знову\(y = x\). Зверніть увагу, зокрема, що дані з\(t\) розподілу дотримуються нормальної кривої досить близько, поки останній десяток або близько того не вказує на кожну крайність.
q-q графіки для нормальних даних із загальним середнім та масштабом
Наше попереднє обговорення\(q-q\) ділянок для нормальних даних все передбачало, що наші дані були стандартизовані. Один з підходів до побудови\(q-q\) ділянок полягає в тому, щоб спочатку стандартизувати дані, а потім продовжити, як описано раніше. Альтернативою є побудова сюжету безпосередньо з необроблених даних.
У цьому розділі ми наведемо загальний підхід до даних, які не стандартизовані. Чому ми стандартизували дані на малюнку\(\PageIndex{12}\)? \(q-q\)Сюжет складається з\(n\) точок
\[\left ( \Phi ^{-1}\left ( \frac{i-5}{n} \right ),z_i \right )\; for\; i=1,2,...,n\]
Якщо вихідні дані {\(z_i\)} нормальні, але мають довільне середнє\(\mu\) і стандартне відхилення\(\sigma\), то лінія не\(y = x\) буде відповідати очікуваним теоретичним квантилям. Зрозуміло, що лінійне перетворення
\[μ + σ ξ_q\]
забезпечить\(q^{th}\) теоретичний квантиль за перетвореною шкалою. На практиці, з новим набором даних\(\{x_1,x_2, \ldots, x_n\}\),
нормальний\(q-q\) сюжет буде складатися з n точок
\[\left ( \Phi ^{-1}\left ( \frac{i-5}{n} \right ),x_i \right )\; for\; i=1,2,...,n\]
Замість побудови лінії\(y = x\) як опорної лінії, лінія
\[y = M + s · x\]
повинні складатися, де\(M\) і\(s\) знаходяться вибіркові моменти (середнє і стандартне відхилення), відповідні теоретичним моментам\(\mu\) і\(\sigma\). Крім того, якщо дані стандартизовані, то лінія\(y = x\) буде доречною, оскільки тепер середнє значення зразка буде\(0\) і стандартне відхилення вибірки буде\(1\).
Приклад\(\PageIndex{1}\): SAT Case Study
Тематичне дослідження SAT слідувало за академічними досягненнями студентів\(105\) коледжів за спеціальністю «інформатика». Перша змінна - це їх словесний бал SAT, а друга - середній бал (GPA) на рівні університету. Перш ніж обчислити статистику висновків за допомогою цих змінних, ми повинні перевірити, чи нормальні їх розподіли. На малюнку\(\PageIndex{13}\) ми виводимо\(q-q\) сюжети словесних змінних SAT і університетських GPA.
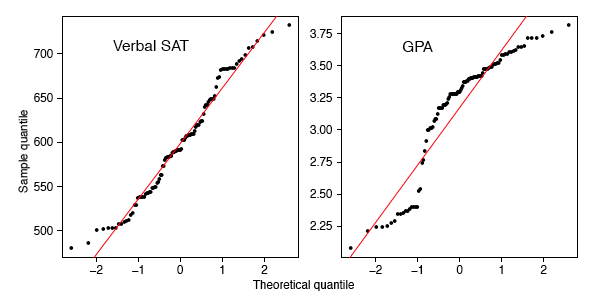
Словесний SAT, здається, досить добре дотримується нормального розподілу, за винятком крайніх хвостів. Однак університетська змінна GPA є дуже ненормальною. Порівняйте графік GPA\(q-q\) з моделюванням у правій рамці малюнка\(\PageIndex{7}\). Ці цифри дуже схожі, за винятком регіону де\(x\approx -1\). Щоб слідувати цим ідеям, ми обчислили гістограми змінних та їх діаграму розкиду на малюнку\(\PageIndex{14}\). Ці цифри розповідають зовсім іншу історію. Університет GPA є бімодальним,\(20\%\) з близько студентів потрапляють в окремий кластер з оцінкою\(C\). Діаграма розкиду досить незвичайна. Хоча студенти в цьому кластері мають нижче середнього словесних балів SAT, є стільки студентів з низькими балами SAT, чий GPA були досить респектабельними. Ми можемо спекулювати щодо причини (ів): різні відволікання, різні звички до вивчення, але це були б лише спекуляції. Але зауважте, що сира кореляція між словесним SAT і GPA є досить високою\(0.65\), але коли ми виключаємо кластер, кореляція для\(86\) решти студентів трохи падає\(0.59\).
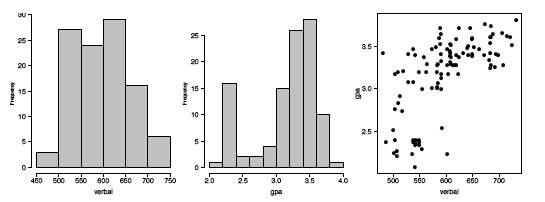
Обговорення
Параметричне моделювання зазвичай передбачає прийняття припущень щодо форми даних або форми залишків від регресійного прилягання. Перевірка таких припущень може приймати різні форми, але дослідження форми за допомогою гістограм і\(q-q\) графіків є дуже ефективним. \(q-q\)Графік не має жодних конструктивних параметрів, таких як кількість бункерів для гістограми.
У просунутому лікуванні\(q-q\) сюжет може бути використаний для формального тестування нульової гіпотези про те, що дані є нормальними. Це робиться шляхом обчислення коефіцієнта кореляції\(n\) точок на\(q-q\) ділянці. Залежно від цього\(n\), нульова гіпотеза відхиляється, якщо коефіцієнт кореляції менше порогового. Поріг вже досить близький до\(0.95\) для скромних розмірів вибірки.
Ми бачили, що\(q-q\) сюжет для рівномірних даних дуже тісно пов'язаний з емпіричною функцією кумулятивного розподілу. Для функцій загальної щільності так зване інтегральне перетворення ймовірності приймає випадкову\(X\) величину і зіставляє її з інтервалом (\(0, 1\)) через CDF\(X\) самого себе, тобто
\[Y = F_X(X)\]
який, як було показано, є рівномірною щільністю. Це пояснює, чому\(q-q\) графік на стандартизованих даних завжди близький до лінії,\(y = x\) коли модель правильна.
Нарешті, вчені роками використовували спеціальний графічний папір, щоб зробити відносини лінійними (прямі). Найпоширенішим прикладом раніше був напівжурнальний папір, на якому точки, що слідують за формулою,\(y=ae^{bx}\) виглядають лінійними. Це випливає, звичайно\(log(y) = log(a) + bx\), оскільки, що є рівнянням для прямої лінії. Графіки\(q-q\) можуть розглядатися як «графічний папір ймовірності», який робить графік впорядкованих значень даних у пряму лінію. Кожна щільність має свою особливу вірогідність графічного паперу.
