Skip to main content
LibreTexts - Ukrayinska

7.5: Стандартний нормальний розподіл

  1. Last updated
  2. Save as PDF
  • Page ID
    98164

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Встановити середнє і стандартне відхилення стандартного нормального розподілу
    • Використовуйте\(Z\) таблицю
    • Скористайтеся звичайним калькулятором
    • Перетворення необроблених даних у\(Z\) бали

    Як обговорювалося у вступному розділі, нормальні розподіли не обов'язково мають однакові кошти і стандартні відхилення. Нормальний розподіл із середнім значенням\(0\) і стандартним відхиленням\(1\) називається стандартним нормальним розподілом.

    Області нормального розподілу часто представлені таблицями стандартного нормального розподілу. Частина таблиці стандартного нормального розподілу наведена в табл\(\PageIndex{1}\).

    Таблиця\(\PageIndex{1}\): Частина таблиці стандартного нормального розподілу
    Z Площа нижче
    -2.5 0,0062
    -2.49 0,0064
    -2.48 0.0066
    -2.47 0.0068
    -2.46 0,0069
    -2.45 0,0071
    -2.44 0.0073
    -2.43 0,0075
    -2.42 0,0078
    -2.41 0,008
    -2.4 0,0082
    -2.39 0,0084
    -2.38 0,0087
    -2.37 0,0089
    -2.36 0,0091
    -2.35 0,0094
    -2.34 0,0096
    -2.33 0,0099
    -2.32 0.0102

    Перший стовпець під назвою\(Z\) "" містить значення стандартного нормального розподілу; другий стовпець містить область нижче\(Z\). Оскільки розподіл має середнє значення\(0\) і стандартне відхилення\(1\),\(Z\) колонка дорівнює числу стандартних відхилень нижче (або вище) середнього. Наприклад, a\(Z\) of\(-2.5\) являє собою значення\(2.5\) стандартних відхилень нижче середнього. Область нижче\(Z\) є\(0.0062\).

    Цю ж інформацію можна отримати за допомогою наступного аплету Java. На малюнку\(\PageIndex{1}\) показано, як він може бути використаний для обчислення площі нижче значення\(-2.5\) за стандартним нормальним розподілом. Зверніть увагу, що середнє значення встановлено,\(0\) а стандартне відхилення встановлено значення\(1\).

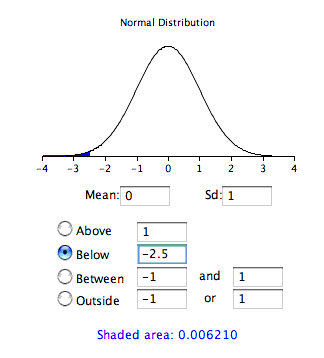
    standard.gif
    Малюнок\(\PageIndex{1}\): Приклад з аплету

    Обчислити площі

    Значення з будь-якого нормального розподілу може бути перетворено у відповідне його значення за стандартним нормальним розподілом за такою формулою:

    \[Z=\frac{X-\mu }{\sigma }\]

    де\(Z\) - значення на стандартному нормальному розподілі,\(X\) - це значення на початковому розподілі,\(\mu\) є середнім показником вихідного розподілу і\(\sigma\) є стандартним відхиленням початкового розподілу.

    Приклад\(\PageIndex{1}\)

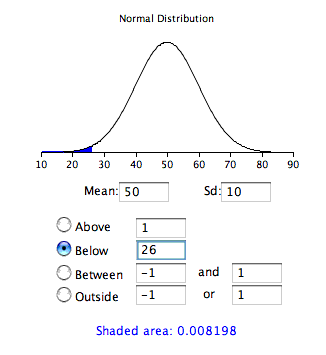
    Як просте застосування, яка частина нормального розподілу із середнім значенням\(50\) і стандартним відхиленням\(10\) нижче\(26\)?

    Рішення

    Застосовуючи формулу, отримуємо

    \[Z = \frac{26 - 50}{10} = -2.4\]

    З таблиці\(\PageIndex{1}\), ми бачимо, що\(0.0082\) of the distribution is below \(-2.4\). There is no need to transform to \(Z\) if you use the applet as shown in Figure \(\PageIndex{2}\).

    standard2.gif
    Малюнок \(\PageIndex{2}\): Площа нижче\(26\) в нормальному розподілі із середнім значенням\(50\) і стандартним відхиленням\(10\)

    Якщо всі значення в розподілі перетворені в\(Z\) бали, то розподіл матиме середнє значення\(0\) і стандартне відхилення\(1\). Цей процес перетворення розподілу на одиницю із середнім значенням\(0\) та стандартним відхиленням\(1\) називається стандартизацією розподілу.