7.2: Історія нормального розподілу

Last updated
Save as PDF

Page ID: 98168

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Дізнайтеся цікаву історію нормальної кривої

У розділі про ймовірність ми побачили, що біноміальний розподіл може бути використаний для вирішення таких проблем, як «Якщо справедлива монета перевертається\(100\) раз, яка ймовірність отримати\(60\) або більше голів?» Імовірність рівно\(x\) голов з\(N\) сальто обчислюється за формулою:

\[P(x)=\frac{N!}{x!(N-x)!}\pi ^x(1-\pi )^{N-x}\]

де\(x\) - число голів (\(60\)),\(N\) - число\(\pi\) сальто (\(100\)), і ймовірність голови (\(0.5\)). Тому, щоб вирішити цю задачу, ви обчислюєте ймовірність\(60\) голів, потім ймовірність\(61\) голів,\(62\) голів і т.д., і складаєте всі ці ймовірності. Уявіть собі, скільки часу потрібно було обчислити біноміальні ймовірності до появи калькуляторів та комп'ютерів.

Авраам де Муавр, статистик\(18^{th}\) століття і консультант азартних гравців, часто закликався зробити ці тривалі обчислення. де Муавр зазначив, що коли кількість подій (сальто монет) збільшилася, форма біноміального розподілу наближалася до дуже гладкої кривої. Біноміальні розподіли для\(2\)\(4\), і\(12\) сальто показані на рис\(\PageIndex{1}\).

Рисунок\(\PageIndex{1}\): *Приклади біноміальних розподілів.* *Висоти синіх смуг представляють ймовірності.*

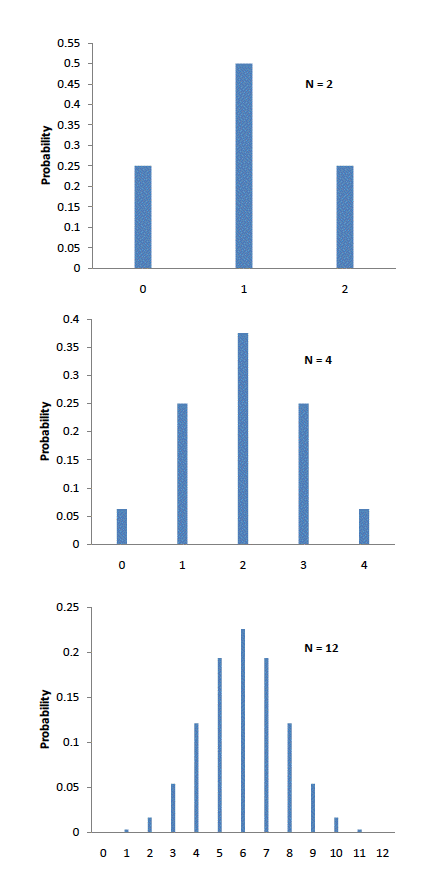
де Муавр міркував, що якби він міг знайти математичний вираз для цієї кривої, він зможе набагато легше вирішити такі проблеми, як пошук ймовірності\(60\) або більшої кількості голів з перегортання\(100\) монет. Це саме те, що він зробив, і крива, яку він виявив, тепер називається «нормальною кривою».

*Рисунок\(\PageIndex{2}\): Нормальне наближення до біноміального розподілу для* *сальто\(12\) монет*

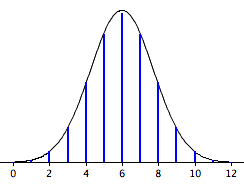
Плавна крива на малюнку\(\PageIndex{2}\) є нормальним розподілом. Зверніть увагу, наскільки добре він наближає біноміальні ймовірності, представлені висотами синіх ліній.

Важливість нормальної кривої випливає насамперед з того, що розподіли багатьох природних явищ хоча б приблизно нормально розподілені. Одним з перших застосувань нормального розподілу було аналіз похибок вимірювань, допущених в астрономічних спостереженнях, помилок, що виникли через недосконалі прилади та недосконалі спостерігачі. Галілей у\(17^{th}\) столітті зазначив, що ці помилки були симетричними і що дрібні помилки траплялися частіше, ніж великі помилки. Це призвело до кількох гіпотезованих розподілів помилок, але лише на початку\(19^{th}\) століття було виявлено, що ці помилки слідують нормальному розподілу. Самостійно математики Адріан ін\(1808\) і Гаусс в\(1809\) розробили формулу нормального розподілу і показали, що похибки добре підходять під цей розподіл.

Цей самий розподіл був виявлений Лапласом,\(1778\) коли він вивів надзвичайно важливу центральну граничну теорему, тему пізнішого розділу цієї глави. Лаплас показав, що навіть якщо розподіл не розподіляється нормально, засоби повторюваних зразків з розподілу будуть дуже майже нормально розподілені, і що чим більший розмір вибірки, тим ближче розподіл засобів до нормального розподілу.

Більшість статистичних процедур тестування відмінностей між засобами припускають нормальні розподіли. Оскільки розподіл засобів дуже близький до нормального, ці тести працюють добре, навіть якщо початковий розподіл є лише приблизно нормальним.

Quételet першим застосував нормальний розподіл до людських особливостей. Він зазначив, що такі характеристики, як зріст, вага та сила, зазвичай розподіляються.