Skip to main content
LibreTexts - Ukrayinska

16.8: Вирішення за невідомий час

  1. Last updated
  2. Save as PDF
  • Page ID
    101677

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Іноді необхідно визначити проміжок часу, який буде потрібно реактивної ланцюга, щоб досягти заданого значення. Це особливо вірно у випадках, коли ми розробляємо RC або L/R ланцюг для виконання точної функції синхронізації. Щоб обчислити це, нам потрібно змінити нашу «Універсальну формулу постійної часу». Оригінальна формула виглядає так:

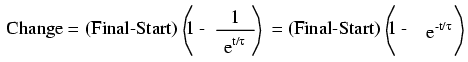
    10263.png

    Однак ми хочемо вирішити на час, а не кількість змін. Для цього алгебраїчно маніпулюємо формулою так, щоб час був сам по собі на одній стороні знака рівності, а всі інші - з іншого боку:

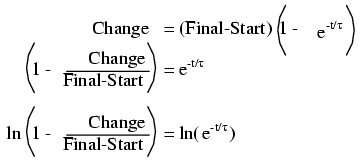
    10276.png

    Позначення ln праворуч від члена постійної часу - це натуральна функція логарифма: точний реверс прийняття потужності e. Насправді дві функції (степені e і натуральні логарифми) можуть бути пов'язані як такі:

    Якщо е х = a, то ln a = х.

    Якщо e x = a, то натуральний логарифм a дасть вам x: потужність, до якої повинна бути піднята e, щоб отримати a.

    Давайте подивимося, як це все працює на реальному прикладі схеми. Взявши ту ж схему резистор-конденсатор з початку глави, ми можемо працювати «назад» від раніше визначених значень напруги, щоб знайти, скільки часу знадобилося, щоб туди потрапити.

    0030 (2) .webp

    Константа часу залишається такою ж величиною: 1 секунда (10 кОм разів 100 мкФ), а початкові/кінцеві значення також залишаються незмінними (E C = 0 вольт стартового і 15 вольт кінцевого). Згідно з нашою діаграмою на початку глави, конденсатор буде заряджений до 12,970 вольт в кінці 2 секунд. Давайте підключимо 12,970 вольт як «Зміна» для нашої нової формули і подивимося, чи дійдемо ми до відповіді 2 секунди:

    10266.png

    Дійсно, ми закінчуємо значенням 2 секунди за час, необхідний для переходу від 0 до 12,970 вольт через конденсатор. Ця варіація формули універсальної постійної часу буде працювати для всіх ємнісних та індуктивних ланцюгів, як «зарядки», так і «розрядки», за умови, що належні значення постійної часу, Start, Final та Change належним чином визначені заздалегідь. Пам'ятайте, найважливішим етапом у вирішенні цих завдань є початкова настройка. Після цього його просто багато натискання кнопки на калькуляторі!

    Рецензія

    • Щоб визначити час, необхідний для RC або L/R ланцюга, щоб досягти певного значення напруги або струму, вам доведеться змінити формулу універсальної постійної часу, щоб вирішити для часу замість зміни.

    10264.png

    • Математичною функцією для реверсування показника «е» є натуральний логарифм (ln), наданий на будь-якому науковому калькуляторі.