Skip to main content
LibreTexts - Ukrayinska

6.3.2: Крива щитів

  1. Last updated
  2. Save as PDF
  • Page ID
    1463

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Шилдс виявив, що «константа» була слабкою функцією зерна числа Рейнольдса, визначеного як:

    \[\text{R e}_* = \dfrac{u_* D}{v}\]

    де:

    \(u_*\) швидкість напруги зсуву \(m/s\)
    \(D\) діаметр зерен \(m\)
    \(v\) кінематичний коефіцієнт в'язкості \(m^2/s\)

    Індексипт* використовується для позначення того, що число Рейнольдса засноване на\(u_*\).

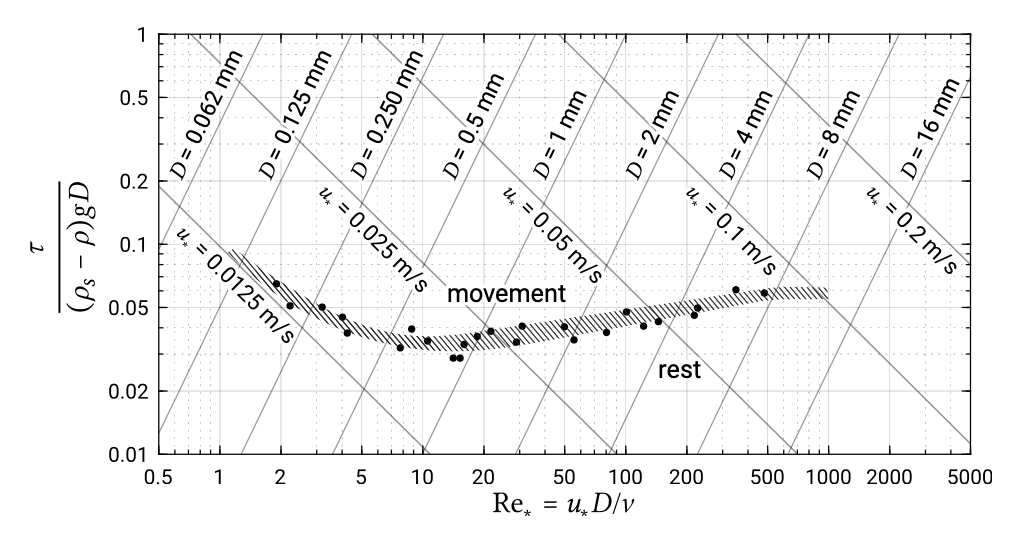
    2021-10-28 г 8.01.17 пнг
    Малюнок 6.5: Крива щитів (Щити, 1936). Зверніть увагу, що осі малюються в масштабі колоди. Лінії постійної\(D\) і\(u_*\) не походять від щитів і утримують постійну щільність\(\rho_s = 2650\ kg/m^3\) і кінематичну в'язкість\(v = 1.25 \times 10^{-6}\ m^2/s\) при температурі води 12 °С.

    На малюнку 6.5 показані виміряні значення як функції\(\text{R e}_*\). Затінена смуга розділяє дві зони: рух частинок осаду спостерігалося в експериментах в зоні над цією затіненою смугою, тоді як руху в зоні під затіненою смугою не спостерігалося. Тому затінена смуга вказує на початок руху. Іноді затінена смуга представлена однією лінією, яку потім називають кривою Щитів. Середнє значення можна побачити приблизно 0,05.

    На жаль, реальність складніша. Серед інших:

    • Крива Щитки справедлива для рівномірного потоку на плоскому ліжку. Вплив брижі в ліжку та вплив поєднання односпрямованого та коливального потоку на ініціювання руху значною мірою невідомі;

    • Градація матеріалу шару може зіграти певну роль, особливо для погано відсортованого осаду (\(D_{90}/D_{10} > 3\)). У цих випадках менші частинки будуть приховані в порожнечах між більшими частинками, тоді як більші частинки більш оголені. Після вимивання оголених більш дрібних частинок залишається верхній шар більш грубих частинок (з більш високими критичними швидкостями потоку) і перешкоджає руху нижчих більш дрібних частинок. Це називається бронею ліжка;

    • Для похилого русла в напрямку потоку можна стверджувати, що критична швидкість потоку буде дещо меншою для похилих вниз ліжок і трохи вище для похилих вгору ліжок;

    • Сили зчеплення між зернами - через наявність зв'язного осаду в ложі - можуть різко збільшити стійкість до ерозії (див. 6.8). Біологічна активність та консолідація можуть бути важливими і в цьому відношенні.

    Незважаючи на ці ускладнення, багато практичних складів для транспортування осаду використовують критичний параметр Shields\(\theta_{cr}\) (ур. 6.3.1.3) і кривої Щитів для визначення початку руху. Серед інших Ван Рейн (1984a) представив криву Щитів як функцію нерозмірного розміру зерна\(D_*\):

    \[D_* = D_{\text{so}} \left (\dfrac{g(s - 1)}{v^2} \right )^{1/3}\]

    Криву Щитків можна представити в терміновому вигляді,\(D_*\) оскільки кожен діаметр зерен має відповідний,\(u_{*, cr}\) як видно на рис. 6.5. При цьому\(\theta_{cr} = f (D_*)\) ніяка ітерація не потрібна для отримання критичного напруження зсуву, як це було б при застосуванні кривої Щитів. Крім того, параметр порога можна скорегувати, щоб врахувати вплив ухилу ліжка\(\tan \alpha\) на поріг руху. Ця формулювання призводить до збільшення критичного напруження зсуву для руху вгору по схилу та зменшення критичного напруження зсуву для руху вниз по схилу. Потім ми маємо формулювання форми:

    \[\theta_{cr} = f (D_*, \tan \alpha)\]