Skip to main content
LibreTexts - Ukrayinska

5.4.1: Хвильові орбітальні швидкості

  1. Last updated
  2. Save as PDF
  • Page ID
    1236

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

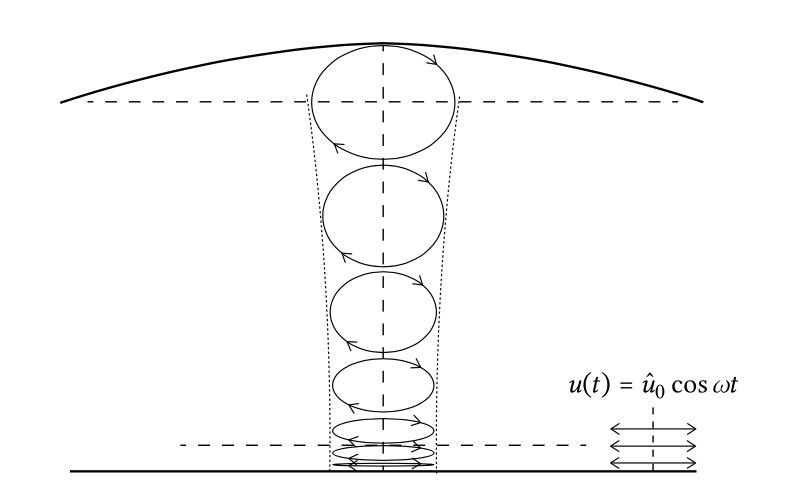
    2021-10-23 пнг
    Малюнок 5.20: Рух частинок води в хвилі скінченної амплітуди на проміжній та малій глибині води.

    Поки ми зосередилися на висоті поверхні хвилі. Під поверхнею хвилі відбувається рух рідини, пов'язаний з рухом водної поверхні; частинки рідини описують орбітальний шлях. До першого порядку (в межах теорії хвиль малої амплітуди Ейрі) орбіти замкнуті 5 кіл у глибокій воді та замкнуті еліпсоїди у воді скінченної глибини, а еліпсоїди стають більш плоскими біля дна. Внизу вертикальні швидкості дорівнюють нулю за визначенням. Чим далі від поверхні, тим менше стає діаметр орбіти. У глибокій воді діаметр орбіти був зменшений лише до 4% від величини на поверхні на глибині половини довжини хвилі. У разі мілководдя частинки води під поширюється хвилею скінченної амплітуди описують еліптичну орбіту. Від поверхні вниз до дна вертикальне зміщення частинок води зводиться до нуля, при цьому горизонтальне зміщення залишається практично постійним (рис.5.20).

    Тепер розглянемо хвилі нескінченно малих амплітуд. Згідно лінійної теорії, горизонтальна орбітальна швидкість змінюється гармонічно з амплітудою,\(\hat{u}\) рівною:

    \[\hat{u} (z) = \omega a \dfrac{\cosh k(h + z)}{\sinh kh}\]

    де:

    \(\omega\) кутова частота\((2\pi /T)\) \(Hz\)
    \(a\) амплітуда хвилі \(m\)
    \(k\) хвильовий номер\((2\pi /L)\) \(1/m\)
    \(L\) довжина хвилі \(m\)
    2021-10-23 пнг
    Малюнок 5.21: Схематичне креслення вертикальних профілів амплітуди швидкості\(\hat{u}\).

    \(z\)-вісь визначається позитивною вгору з\(z = 0\) на поверхні і\(z = -h\) внизу. Швидкість\(u\) знаходиться в напрямку поширення хвилі. Використання\(\cosh kh\) та\(\sinh kh\) наближень для дрібної та глибокої води (App. А) профілі горизонтальних швидкостей можна накреслити схематично, як на рис.5.21.

    На мілководді (\(kh \ll 1\); на практиці\(kh < \pi /10\) або\(h/L > 1/20\)), рівномірна по глибині амплітуда швидкості задається (див. 3.8.1.8):

    \[\hat{u} = \dfrac{\omega a}{kh} = c \dfrac{a}{h} = \sqrt{gh} \dfrac{H}{2h}\]

    Екскурсії частинок (тобто горизонтальні та вертикальні переміщення частинок) є часовими інтегралами коливальних горизонтальних та вертикальних швидкостей потоку відповідно. Це означає, що амплітуда горизонтальної екскурсії частинки задається:

    \[\hat{\xi} = \dfrac{\hat{u}}{\omega}\]

    Зверніть увагу, що Сект. 5.3 описано, як у мілкових хвиль піднесення поверхні стає поступово більш скошеною і асиметричною. Звичайно хвильові орбітальні швидкості біля ліжка також стануть косими і асиметричними. Хоча лінійне наближення не описує мінливу форму хвилі, величину орбітальної швидкості можна оцінити досить добре, використовуючи лінійну теорію хвиль.

    5. При другому порядку шляху частинок більше не замкнуті орбіти і відбувається дрейф або масовий транспорт у напрямку поширення хвилі (Sect. 5.5.1).