1.6: Операції з матрицями

У попередньому розділі ми побачили важливий зв'язок між лінійними функціями та матрицями. У цьому розділі ми обговоримо різні операції над матрицями, які нам знадобляться в нашій подальшій роботі з лінійними функціями.

Алгебра матриць

Якщо$M$ $n \times m$матриця with$a_{i j}$ в$i$ -му рядку і$j$ й стовпці$i=1,2, \ldots, n, j= 1,2, \ldots, m$, то напишемо$M=\left[a_{i j}\right]$. За допомогою цього позначення визначення додавання, віднімання та скалярного множення для матриць є прямими.

Визначення$\PageIndex{1}$

Припустимо$N=\left[b_{i j}\right]$,$M=\left[a_{i j}\right]$ і є$n \times m$ матрицями і$c$ є дійсним числом. Потім визначаємо

$$M+N=\left[a_{i j}+b_{i j}\right],$$

$$M-N=\left[a_{i j}-b_{i j}\right],$$

і

$$c M=\left[c a_{i j}\right] .$$

Іншими словами, ми визначаємо додавання, віднімання та скалярне множення для матриць, виконуючи ці операції над окремими елементами матриць, подібно до того, як ми виконуємо ці операції над векторами.

Приклад$\PageIndex{1}$

Якщо

\ [M=\ left [\ begin {масив} {rrr}
1 & 2 & 3\\
-5 & 3 & -1
\ end {масив}\ праворуч]\ nonumber\]

і

\ [N=\ left [\ begin {масив} {rrr}
3 & 1\\
1 & -3 & 2
\ end {масив}\ праворуч],\ nonumber\]

то, наприклад,

\ [\ почати {вирівняний}
&M+N=\ лівий [\ почати {масив} {rrr}
1+3 & 2+1 & 3+4\\
-5+1 & 3-3 & -1+2
\ кінець {масив}\ справа] =\ лівий [\ початок {масив} {rrr}
4 & 3\\
-4 & 0 & 1
\ кінець {масив}\ праворуч], \\
&M-N=\ лівий [\ почати {масив} {rrr}
1-3 & 2-1 & 3-4\\
-5-1 & 3+3 & -1-2
\ кінець {масив}\ справа] =\ лівий [\ begin {масив} {lll}
-2 & 1\\
-6 & 6 & -3
\ end {масив}\ праворуч],
\ end {вирівняний}\ nonumber\]

і

\ [3 M=\ лівий [\ begin {масив} {rrr}
3 & 6 & 9\\
-15 & 9 & -2
\ end {масив}\ праворуч]. \ номер\]

Ці операції мають природні інтерпретації з точки зору лінійних функцій. Припустимо$K: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ ,$L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ і є лінійними з$L(\mathbf{x})=M \mathbf{x}$ і$K(\mathbf{x})=N \mathbf{x}$ для$n \times m$ матриць$M$ і$N$. Якщо ми$L+K: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ визначимо

$$(L+K)(\mathbf{x})=L(\mathbf{x})+K(\mathbf{x}) ,$$

потім

$$(L+K)\left(\mathbf{e}_{j}\right)=L\left(\mathbf{e}_{j}\right)+K\left(\mathbf{e}_{j}\right)$$

для$j=1,2, \ldots, m$. Звідси$j$ й стовпець матриці,$L+K$ який представляє собою суму$j$ го стовпців$M$ і$N$. Іншими словами,

$$(L+K)(\mathbf{x})=(M+N) \mathbf{x}$$

для всіх$\mathbf{x}$ в$\mathbb{R}^{m}$. Аналогічно, якщо ми$L-K: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ визначимо

$$(L-K)(\mathbf{x})=L(\mathbf{x})-K(\mathbf{x}) ,$$

потім

$$(L-K)(\mathbf{x})=(M-N) \mathbf{x} .$$

Якщо, для будь-якого скаляра$c$, ми визначаємо$c L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ по

$$c L(\mathbf{x})=c(L(\mathbf{x})) ,$$

потім

$$c L\left(\mathbf{e}_{j}\right)=c\left(L\left(\mathbf{e}_{j}\right)\right)$$

для$j=1,2, \ldots, m$. Звідси$j$ й стовпець матриці, який представляє,$cL$ є скалярним,$c$ кращим від$j$ го стовпця$M$. Тобто,

$$c L(\mathbf{x})=(c M) \mathbf{x}$$

для всіх$\mathbf{x}$ в$\mathbb{R}^{m}$. Коротше кажучи, операції додавання, віднімання та скалярного множення для матриць природним чином відповідають операціям додавання, віднімання та скалярного множення для лінійних функцій.

Тепер розглянемо випадок, де$L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{p}$ і$K: \mathbb{R}^{p} \rightarrow \mathbb{R}^{n}$ знаходяться лінійні функції. $M$Дозволяти$p \times m$ матриця така, що$L(\mathbf{x})=M \mathbf{x}$ для всіх$\mathbf{x}$ в$\mathbb{R}^{m}$ і нехай$N$ буде$n \times p$ матриця така, що$K(\mathbf{x})=N \mathbf{x}$ для всіх$\mathbf{x}$ в$\mathbb{R}^{p}$. Так як для будь-якого$\mathbf{x}$ в$\mathbb{R}^{m}$,$L(\mathbf{x})$ знаходиться в$\mathbb{R}^{p}$, ми можемо сформувати$K \circ L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$, склад$K$ з$L$, визначається

$$K \circ L(\mathbf{x})=K(L(\mathbf{x})).$$

Зараз

$$K(L(\mathbf{x}))=N(M \mathbf{x}) ,$$

тому було б природно визначити$NM$, добуток матриць$N$ і$M$, щоб бути матрицею$K \circ L$, в цьому випадку ми б

$$N(M \mathbf{x})=(N M) \mathbf{x}.$$

Таким чином, ми хочемо, щоб$j$ той стовпець$NM$$j=1,2, \ldots, m$,, бути

$$K \circ L\left(\mathbf{e}_{j}\right)=N\left(L\left(\mathbf{e}_{j}\right)\right),$$

який є лише точковим$L\left(\mathbf{e}_{j}\right)$ добутком з рядків$N$. Але$L\left(\mathbf{e}_{j}\right)$ це$j$ й стовпець$M$, тому стовпець з$NM$ формується шляхом прийняття точкового добутку$j$ го стовпця$M$ з рядків$N$.$j$ Іншими словами, запис у$i$ -му рядку та$j$ стовпці$NM$ - це крапковий$i$ добуток го рядка$N$ з$j$ го стовпчика$M$. Ми виписуємо це явно в наступному визначенні.

Визначення$\PageIndex{2}$

Якщо$N=\left[a_{i j}\right]$$n \times p$ матриця і$M=\left[b_{i j}\right]$ є$p \times m$ матрицею, то визначаємо добуток$N$ і$M$ бути$n \times m$ матрицею$N M=\left[c_{i j}\right]$, де

$$c_{i j}=\sum_{k=1}^{p} a_{i k} b_{k j} ,$$

$i=1,2, \ldots, n \text { and } j=1,2, \ldots, m .$

Зауважте, що$NM$ є$n \times m$ матрицею, оскільки$K \circ L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$. Причому$NM$ добуток двох матриць$N$ і$M$ визначається тільки тоді, коли кількість стовпців$N$ дорівнює числу рядків$M$.

Приклад$\PageIndex{2}$

Якщо

\ [N=\ left [\ begin {масив} {rr}
1 & 2\\
-1 & 3\\
2 & -2
\ end {масив}\ праворуч]\ nonumber\]

і

\ [M=\ left [\ begin {масив} {rrrr}
2 & -2 & 1\\
1 & 2 & -1 & -2
\ end {масив}\ праворуч],\ nonumber\]

потім

\ begin {вирівняний}
N M &=\ лівий [\ begin {масив} {rr}
1 & 2\\
-1 & 3\
2 & -2
\ кінець {масив}\ праворуч]\ лівий [\ begin {масив} {rrrr}
2 & -2 & 1\\
1 & 2 & 1 & 2 & -1 & -2
\ кінець {масив}\ праворуч]\\
&=\ ліворуч [\ почати {масив} {rrrr}
2+2 & -2+4 & 1-2\\
-2+3 & 2+6 & -1-3 & -3-6\\
4-2 & -4-4 & 2+2 & 6+4
\ end {масив}\ праворуч]\\
&=\ лівий [\ почати {масив} {rrrr}
4 & 2 & -1 & -1\\
1 & 8 & -4 & -9\\
2 & -8 & 4 & 10
\ end {масив}\ праворуч].
\ end {вирівняний}

Зверніть увагу, що$N$ є$3 \times 2$,$M$ є$2 \times 4$, і$NM$ є$3 \times 4$. Також врахуйте, що неможливо сформувати товар в іншому порядку.

Приклад$\PageIndex{3}$

$L: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}$Дозволяти лінійну функцію, визначену

$$L(x, y)=(3 x-2 y, x+y, 4 y) \nonumber$$

і нехай$K: \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}$ буде лінійна функція, визначена

$$K(x, y, z)=(2 x-y+z, x-y-z). \nonumber$$

Тоді матриця$L$ для

\ [M=\ left [\ begin {масив} {rr}
3 & -2\\
1 & 1\\
0 & 4
\ end {масив}\ праворуч],\ nonumber\]

матриця$K$ для

\ [N=\ left [\ begin {масив} {rrr}
2 & -1 & 1\
1 & -1 & -1
\ end {масив}\ праворуч],\ nonumber\]

і матриця$K \circ L: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ для

\ [N M =\ лівий [\ початок {масив} {rrr}
2 & -1 & 1\
1 & -1 & -1
\ кінець {масив}\ праворуч]\ лівий [\ початок {масив} {rr}
3 & -2\\
1 & 1\\
0 & 4
\ end {масив}\ праворуч] =\ left [\ begin {масив} {ll}
6-1+0 & -4-1+4\\
3-1+0 & -2-1-4
\ end {масив}\ праворуч] =\ лівий [\ begin {масив} {ll}
5 & -1\\
2 & -7
\ end {масив}\ праворуч]. \ номер\]

Іншими словами,

\ [K\ circ L (x, y) =\ лівий [\ почати {масив} {ll}
5 & -1\\
2 & -7
\ кінець {масив}\ праворуч]\ лівий [\ початок {масив} {l}
x\
y
\ кінець {масив}\ праворуч] =\ лівий [\ початок {масив} {c}
5 x-y\
2 x-7 y
\ кінець {масив}\ право]. \ номер\]

Відзначимо, що саме в цьому випадку можна сформувати композицію в іншому порядку. Матриця$L \circ K: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ для

\ [M N =\ лівий [\ початок {масив} {rr}
3 & -2\\
1 & 1\\
0 & 4
\ кінець {масив}\ праворуч]\ лівий [\ початок {масив} {rrr}
2 & -1 &
1\ -1 & -1
\ кінець {масив}\ праворуч] =\ лівий [\ почати {масив} {rrr}
6-2 & -3+2 & 3+2\\
2+1 & -1-1 & 1-1\\
0+4 & 0-4 & 0-4
\ кінець {масив}\ праворуч] =\ лівий [\ почати {масив} {rrr}
4 & -1 & 5\\
3 & -2 & 0\\
4 & -4 & -4 & -4
\ кінець {масив }\ право],\ nonnumber\]

і так

\ [L\ circ K (x, y, z) =\ лівий [\ почати {масив} {rrr}
4 & -1 & 5\\
3 & -2 & 0\\
4 & -4 & -4
\ end {масив}\ справа]\ лівий [\ початок {масив} {l}
x\
y\
z
\ кінець {масив}\ праворуч] =\ лівий [\ почати {масив} {c}
4 x-y+5 z\\
3 x-2 y\\
4 x-4 y-4 z
\ end {масив}\ праворуч]. \ номер\]

Зокрема, відзначимо, що не тільки є$N M \neq M N$, але насправді$NM$ і$MN$ навіть не однакового розміру.

Детермінанти

Поняття детермінанти матриці тісно пов'язане з ідеєю площі та обсягу. Для початку нашого визначення розглянемо$2 \times 2$ матрицю

\ [M=\ left [\ begin {масив} {ll}
a_ {1} & a_ {2}\\
b_ {1} & b_ {2}
\ end {масив}\ праворуч]\ nonumber\]

Малюнок$\PageIndex{1}$: Паралелограм в$\mathbb{R}^{2}$ з суміжними сторонами$\mathbf{a}$ і$\mathbf{b}$

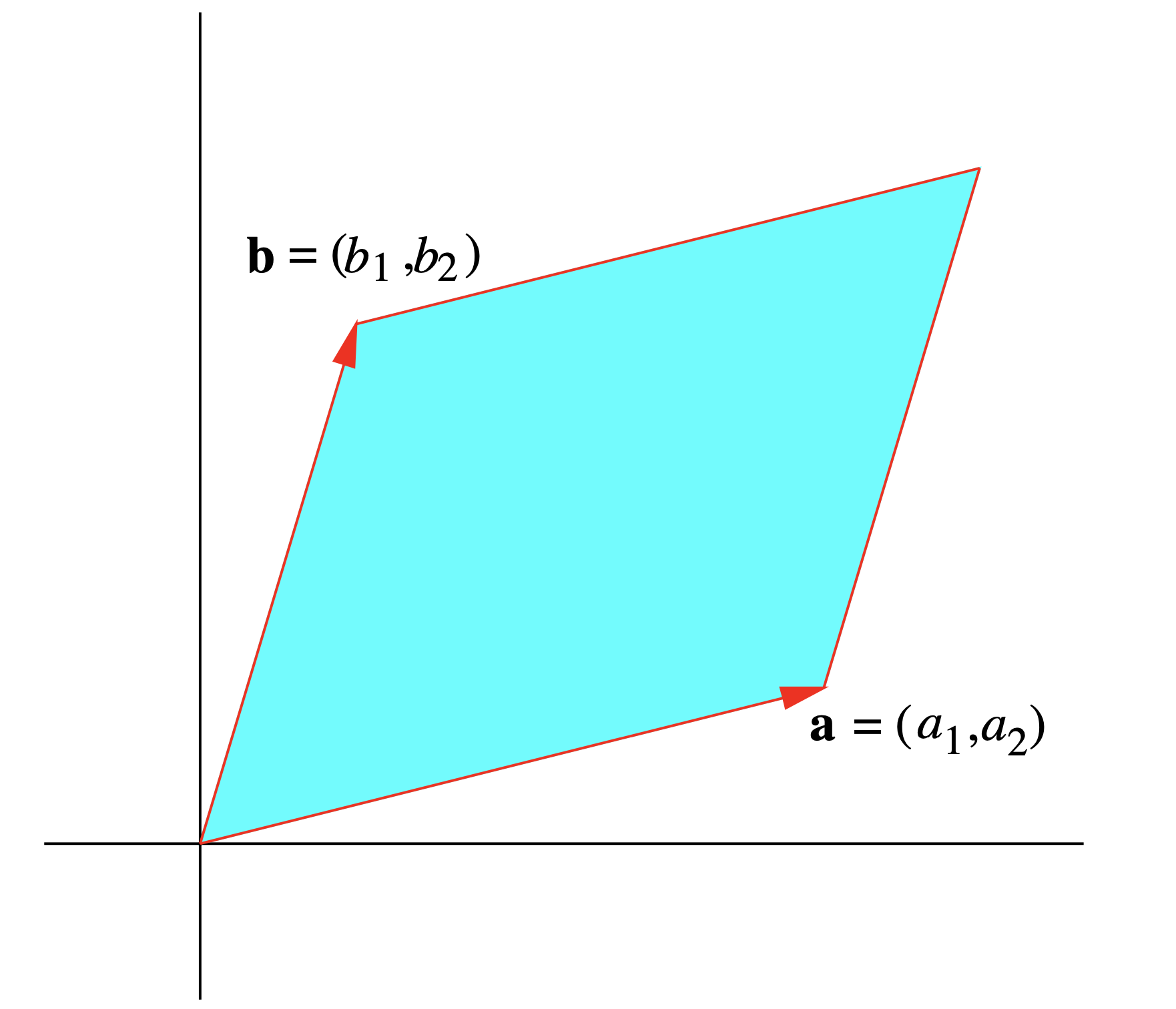
і нехай$\mathbf{a}=\left(a_{1}, a_{2}\right)$ і$\mathbf{b}=\left(b_{1}, b_{2}\right)$. Якщо$P$ паралелограм, який має$\mathbf{a}$ і$\mathbf{b}$ для суміжних сторін і$A$ є площею$P$ (див. Рис. 1.6.1), то ми побачили в розділі 1.3 що

$$A=\left\|\left(a_{1}, a_{2}, 0\right) \times\left(b_{1}, b_{2}, 0\right)\right\|=\|\left(0,0, a_{1} b_{2}-a_{2} b_{1} \|=\left|a_{1} b_{2}-a_{2} b_{1}\right|\right. .$$

Це мотивує наступне визначення.

Визначення$\PageIndex{3}$

Задано$2 \times 2$ матрицю

\ [M=\ left [\ begin {масив} {ll}
a_ {1} & a_ {2}\\
b_ {1} & b_ {2}
\ кінець {масив}\ праворуч],\ nonumber\]

визначник$M$, позначається det ($M$), є

$$\operatorname{det}(M)=a_{1} b_{2}-a_{2} b_{1} . \label{1.6.18}$$

Звідси ми маємо$A=|\operatorname{det}(M)|$. Словом, для$2 \times 2$ матриці$M$ абсолютне значення детермінанта$M$ дорівнює площі паралелограма, який має рядки$M$ для сусідніх сторін.

Приклад$\PageIndex{4}$

У нас є

\ [\ ім'я оператора {det}\ left [\ begin {масив} {rr}
1 & 3\\
-4 & 5
\ end {масив}\ справа] =( 1) (5) - (3) (-4) =5+12=17. \ номер\]

Тепер розглянемо$3 \times 3$ матрицю

\ [M=\ лівий [\ почати {масив} {lll}
a_ {1} & a_ {2} & a_ {3}\\
b_ {1} & b_ {2} & b_ {2} & b_ {3}\\
c_ {1} & c_ {2} & c_ {3}
\ кінець {масив}\ праворуч]\ nonumber\]

і нехай$\mathbf{a}=\left(a_{1}, a_{2}, a_{3}\right)$$\mathbf{b}=\left(b_{1}, b_{2}, b_{3}\right)$, і$\mathbf{c}=\left(c_{1}, c_{2}, c_{3}\right)$. Якщо$V$ обсяг паралелепіпеда$P$ з сусідніми ребрами$\mathbf{a}$$\mathbf{b}$, і$\mathbf{c}$, то, знову з розділу 1.3,

\ [\ почати {вирівняти}
V &=|\ mathbf {a}\ точка (\ mathbf {b}\ раз\ mathbf {c}) |\ номер\
&=\ ліворуч | a_ {1}\ ліворуч (b_ {2} c_ {3} -b_ {3} c_ {2}\ праворуч) +a_ {2}\ ліворуч (b_ {3} c_ {1} -b_ {1} c_ {3}\ праворуч) +a_ {3}\ ліворуч (b_ {1} c_ {2} -b_ {2} c_ {1}\ праворуч)\\ nonnumber\\
&=\ left|a_ {1}\ ім'я оператора {det}\ left [\ begin {масив} {ll}
b_ {2} & b_ {3}\ nonumber\\
c_ {2} & c_ {3}
\ кінець {масив}\ справа] -a_ {2}\ ім'я оператора {det}\ left [\ begin {масив} {ll}
b_ {1} & b_ {3}\ nonumber\
c_ {1} & c_ {3}
\ end {масив}\ право] +a_ {3}\ ім'я оператора {det}\ left [\ begin {масив} {ll}
b_ {1} & b_ {2}\ nonumber\\
c_ {1} & c_ {2}
\ end {масив}\ право]\ right|. \ етикетка {}
\ end {вирівняти}\]

Визначення$\PageIndex{4}$

Задано$3 \times 3$ матрицю

\ [M=\ лівий [\ почати {масив} {lll}
a_ {1} & a_ {2} & a_ {3}\\
b_ {1} & b_ {2} & b_ {2} & b_ {3}\\
c_ {1} & c_ {2} & c_ {3}
\ кінець {масив}\ праворуч],\ nonumber\]

визначник$M$, позначається det ($M$), є

\ [\ ім'я оператора {det} (M) =a_ {1}\ ім'я оператора {det}\ left [\ begin {масив} {ll}
b_ {2} & b_ {3}\\
c_ {2} & c_ {3}
\ кінець {масив}\ справа] -a_ {2}\ ім'я оператора {det}\ left [\ begin {масив} {ll}
b_ {1} & b_ {3}\\
c_ {1} & c_ {3}
\ end { масив}\ праворуч] +a_ {3}\ ім'я оператора {det}\ left [\ begin {масив} {ll}
b_ {1} & b_ {2}\\
c_ {1} & c_ {2}
\ end {масив}\ право]. \ етикетка {1.6.20}\]

Аналогічно$2 \times 2$ випадку, у нас є$V=|\operatorname{det}(M)|$.

Приклад$\PageIndex{5}$

У нас є

\ begin {вирівняний}
\ ім'я оператора {det}\ left [\ begin {масив} {llr}
2 & 3 & 9\\
2 & 1 & -4\\
5 & 1 & -1
\ end {масив}\ праворуч] &=2\ ім'я оператора {det}\ left [\ begin {масив} {cc}
1 & -4\\
1 & amp; -1
\ end {масив}\ праворуч] -3\ ім'я оператора {det}\ left [\ begin {масив} {cc}
2 & -4
\
5 & -1\ кінець {масив}\ праворуч] +9\ ім'я оператора {det}\ left [\ begin {масив} {cc}
2 & 1\

\ end {масив}\ праворуч]\
&=2 (-1+4) -3 (-2+20) +9 (2-5)\\
&=6-54-27\\
&=-75.
\ end {вирівняний}

Задано$n \times n$ матрицю$M=\left[a_{i j}\right]$, нехай$M_{i j}$ буде$(n-1) \times(n-1)$ матриця, отримана шляхом видалення$i$ го рядка та$j$ стовпчика$M$. Якщо для$n=1$ ми спочатку визначаємо$\operatorname{det}(M)=a_{11}$ (тобто детермінант$1 \times 1$ матриці - це лише значення її єдиного запису), то ми могли б висловити$n=2$, для, визначення детермінанти$2 \times 2$ матриці, заданої в ($\ref{1.6.18}$) у вигляді

$$\operatorname{det}(M)=a_{11} \operatorname{det}\left(M_{11}\right)-a_{12} \operatorname{det}\left(M_{12}\right)=a_{11} a_{22}-a_{12} a_{21}.$$

Аналогічно$n=3$, з, ми могли б висловити визначення$M$ детермінанти заданого в ($\ref{1.6.20}$) у формі

$$\operatorname{det}(M)=a_{11} \operatorname{det}\left(M_{11}\right)-a_{12} \operatorname{det}\left(M_{12}\right)+a_{13} \operatorname{det}\left(M_{13}\right).$$

За цією схемою ми можемо сформувати рекурсивне визначення детермінанти$n \times n$ матриці.

Визначення$\PageIndex{5}$

Припустимо,$M=\left[a_{i j}\right]$ це$n \times n$ матриця і нехай$M_{i j}$ буде$(n-1) \times(n-1)$ матриця, отримана шляхом видалення$i$ го рядка і$j$ го стовпця$M$,$i=1,2, \ldots, n$ і$j=1,2, \ldots, n$. Для$n=1$, визначаємо детермінант$M$, позначається$\operatorname{det}(M)$, по

$$\operatorname{det}(M)=a_{11}$$

Для$n > 1$, визначаємо детермінант$M$, позначається$\operatorname{det}(M)$, по

\ [\ begin {вирівнювання}
\ ім'я оператора {det} (M) &=a_ {11}\ ім'я оператора {det}\ left (M_ {11}\ праворуч) -a_ {12}\ ім'я оператора {det}\ left (M_ {12}\ праворуч) +\ cdots+ (-1) ^ {1+n} a_ {1 n}\ ім'я оператора {det}\ ліворуч (M_ {1 n}\ праворуч)\ номер\\
&=\ sum_ {j=1} ^ {n} (-1) ^ {1+j} a_ {1 j}\ ім'я оператора {det}\ left (M_ {1 j}\ праворуч). \ етикетка {1.6.24}
\ кінець {вирівнювання}\]

Ми називаємо визначення рекурсивним, тому що ми визначили детермінант$n \times n$ матриці через детермінант$(n-1) \times(n-1)$ матриць, які, в свою чергу, визначаються через детермінант$(n-2) \times(n-2)$ матриць і так далі, поки ми не звели задачу до обчислення детермінанти$1 \times 1$ матриць.

Приклад$\PageIndex{6}$

Для прикладу детермінанти$4 \times 4$ матриці ми маємо

\ begin {вирівняний}
\ ім'я оператора {det}\ left [\ begin {масив} {rrrr}
2 & 1 & 3\
2 & 1 & 1\\ 2 & 1\\
-2 & 3 & -1 & 2\\
1 & 1 & 1
\ end {масив}\ праворуч] =2 &\\ ім'я оператора {det}\ ліворуч [\ почати {масив} {rrr}
1 & 4 & 1\\
3 & -1 & 2\\
2 & 1 & 1
\ кінець {масив}\ право] -\ ім'я оператора {det}\ left [\ begin {масив} {rrr}
2 & 4 & 1\
-2 & -1 & 2\\
1 & 11 & amp; 1
\ кінець {масив}\ праворуч]\\
&+3\ ім'я оператора {det}\ лівий [\ begin {масив} {rrr}
2 & 1\\
-2 & 3\\
1 & 2 & 2 & 1
\ end {масив}\ справа] -2\ ім'я оператора {det}\ left [\ почати {масив} {rrr}
2 & 1 & 4\\
-2 & 3 & -1\\
1 & 1 & 1
\ кінець {масив}\ праворуч]\\
=& 2 (-1-2) -4 (3-4) + (3+2)) - (2 (-1-2)\\
&\ quad-4 (-2-2) + (-2+1)) +3 (2 (3-4) - (-2-2)\\
&+ (-4-3) -2 (2 (3+2) - (-2+1) +4 (-4-3))\\
=& 2 (-3+4+5) - (-6+16-1) +3 (-2+4-7)\\
&\ квадро-2 (10+1-28)\\
=& 12-9-15+34\\
=& 22.
\ end {вирівняний}

Наступна теорема стверджує, що немає нічого особливого у використанні першого рядка матриці в розширенні детермінанти, зазначеної в ($\ref{1.6.24}$), а також немає нічого особливого щодо розширення вздовж рядка замість стовпця. Практичний ефект полягає в тому, що ми можемо обчислити детермінант даної матриці, що розширюється вздовж того, який рядок або стовпчик є найбільш зручним. Доказ цієї теореми приведе нас занадто далеко на цьому етапі, тому ми опустимо її (але вас попросять перевірити теорему для особливих випадків$n=2$ та$n=3$ у вправі 10).

Теорема$\PageIndex{1}$

$M=\left[a_{i j}\right]$Дозволяти$n \times n$ матриця і$M_{i j}$ нехай$(n-1) \times(n-1)$ матриця отримана шляхом видалення$i$ го рядка і$j$ го стовпця$M$. Тоді для будь-якого$i=1,2, \ldots, n$,

$$\operatorname{det}(M)=\sum_{j=1}^{n}(-1)^{i+j} a_{i j} \operatorname{det}\left(M_{i j}\right),$$

і для будь-якого$j=1,2, \ldots, n$,

$$\operatorname{det}(M)=\sum_{i=1}^{n}(-1)^{i+j} a_{i j} \operatorname{det}\left(M_{i j}\right), \label{1.6.26}$$

Приклад$\PageIndex{7}$

Найпростіший спосіб обчислення визначника матриці

\ [M=\ left [\ begin {масив} {rrr}
4 & 0 & 3\\
2 & 3 & 1\\
-3 & 0 & -2
\ кінець {масив}\ праворуч]\ nonumber\]

полягає в розширенні уздовж другого стовпчика. А саме,

\ begin {вирівняний}
\ ім'я оператора {det} (M) =& (-1) ^ {1+2} (0)\ ім'я оператора {det}\ left [\ begin {масив} {rr}
2 & 1\
-3 & -2
\ end {масив}\ праворуч] + (-1) ^ {2+2} (3)\ ім'я оператора {det}\ left [\ begin {масив} {rr}
4 & 3\\
-3 & -2
\ end {масив}\ праворуч]\\
&+ (-1) ^ {3+2} (0)\ ім'я оператора {det}\ left [\ begin {масив} {ll}
4 & 3\\
2 & 1
\ end {масив}\ праворуч]\\
=& 3 (-8+9)\\
=& 3.
\ end {вирівняний}

Слід переконатися, що розширення уздовж першого ряду, як ми це робили при визначенні детермінанта, дає той же результат.

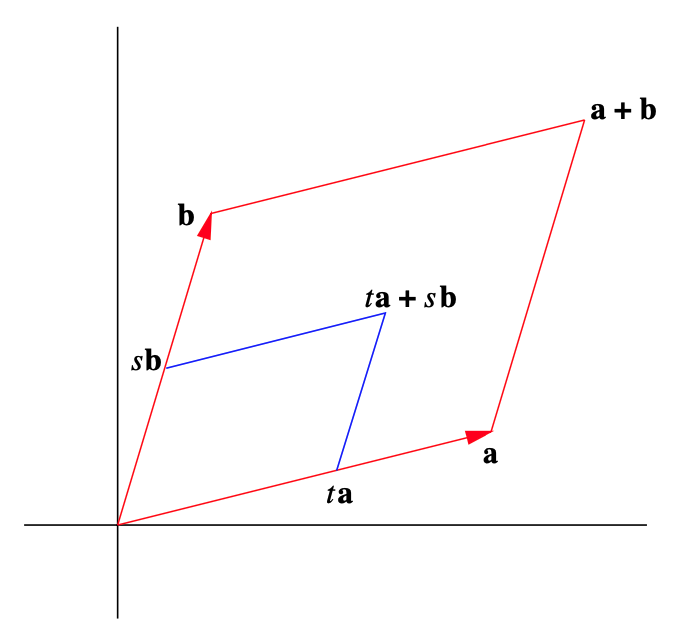
Для того щоб повернутися до проблеми обчислення обсягів, нам потрібно визначити паралелепіпед в$\mathbb{R}^{n}$. Спочатку зауважте, що якщо$P$ є паралелограмом в$\mathbb{R}^{2}$ з сусідніми сторонами, заданими векторами$\mathbf{a}$ і$\mathbf{b}$, то

$$P=\{\mathbf{y}: \mathbf{y}=t \mathbf{a}+s \mathbf{b}, 0 \leq t \leq 1,0 \leq s \leq 1\}.$$

Тобто, for$0 \leq t \leq 1$,$\text { ta }$ є точкою між$\mathbf{0}$ і$\mathbf{a}$, і for$0 \leq s \leq 1$,$s \mathbf{b}$ є точкою між$\mathbf{0}$ і$\mathbf{b}$; отже$t \mathbf{a}+s \mathbf{b}$, точка в паралелограмі$P$. Причому кожен пункт в$P$ може бути виражений саме в такому вигляді. Див. Малюнок 1.6.2. Наступне визначення узагальнює цю характеристику паралелограм.

Малюнок$\PageIndex{2}$: Паралелограм в$\mathbb{R}^{2}$ з суміжними сторонами$\mathbf{a}$ і$\mathbf{b}$

Визначення$\PageIndex{6}$

$\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}$Дозволяти лінійно незалежні вектори в$\mathbb{R}^{n}$. Дзвонимо

$$P=\left\{\mathbf{y}: y=t_{1} \mathbf{a}_{1}+t_{2} \mathbf{a}_{2}+\cdots+t_{n} \mathbf{a}_{n}, 0 \leq t_{i} \leq 1, i=1,2, \ldots, n\right\}$$

n-мірний паралелепіпед з сусідніми ребрами$\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}$.

Визначення$\PageIndex{7}$

$P$Дозволяти n -мірний паралелепіпед з сусідніми ребрами$\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}$ і$M$ нехай$n \times n$ матриця, яка має$\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}$ для своїх рядків. Тоді обсяг$P$ визначається бути$|\operatorname{det}(M)|$.

За допомогою ($\ref{1.6.26}$) та індукції може бути показано, що якщо$N$ матриця отримана шляхом зміни рядків та стовпців$n \times n$ матриці$M$, то$\operatorname{det}(N)=\operatorname{det}(M)$ (див. Вправа 12). Таким чином, ми могли б визначити$M$ в попередньому визначенні, використовуючи$\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}$ для стовпців, а не рядків.

Тепер припустимо$L: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ , лінійний і нехай$M$ буде$n \times n$ матриця така, що$L(\mathbf{x})=M \mathbf{x}$ для всіх$\mathbf{x}$ в$\mathbb{R}^{n}$. $C$Дозволяти$n$ -мірний паралелепіпед з суміжними ребрами$\mathbf{e}_{1}, \mathbf{e}_{2}, \ldots, \mathbf{e}_{n}$, стандартні базисні вектори для$\mathbb{R}^{n}$. Тоді$C$ $1 \times 1$квадрат коли$n=2$ і$1 \times 1 \times 1$ куб коли$n=3$. Загалом, ми можемо розглядати$C$ як$n$ -мірний одиничний куб. Зверніть увагу, що обсяг$C$ є, за визначенням,

\ [\ ім'я оператора {det}\ лівий [\ почати {масив} {ccccc}
1 & 0 & 0 &\ cdots &
0\\ 0 & 1 & 0 & 0 & 0\\
cdots & 0\\ 0 & 0 &
\ cdots &
0\\ vdots &\ vdots &\\ dots\\ підсилювач; 0 & 0 &\ cdots & 1
\ end {масив}\ праворуч] =1. \ номер\]

Припустимо$L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)$, лінійно незалежні і нехай$P$ бути$n$ -мірний паралелепіпед з сусідніми ребрами$L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)$. Зверніть увагу, що якщо

$$\mathbf{x}=t_{1} \mathbf{e}_{1}+t_{2} \mathbf{e}_{2}+\cdots+t_{n} \mathbf{e}_{n} , \nonumber$$

де$0 \leq t_{k} \leq 1$ для$k=1,2, \ldots, n$, це точка в$C$, то

$$L(\mathbf{x})=t_{1} L\left(\mathbf{e}_{1}\right)+t_{2} L\left(\mathbf{e}_{2}\right)+\cdots+t_{n} L\left(\mathbf{e}_{n}\right) \nonumber$$

це точка в$P$. Фактично,$L$ відображає n -вимірний одиничний куб$C$ точно на$n$ - розмірний паралелепіпед$P$. Оскільки$L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)$ є стовпцями$M$, то випливає, що обсяг$P$ дорівнює$|\operatorname{det}(M)|$. Іншими словами,$|\operatorname{det}(M)|$ вимірює, наскільки$L$ розтягує або зменшує об'єм одиничного куба.

Теорема$\PageIndex{2}$

Припустимо$L: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ , є$M$ лінійним і є$n \times n$ матриця така, що$L(\mathbf{x})=M \mathbf{x}$. Якщо$L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)$ лінійні незалежні і являють$P$ собою$n$ -мірний паралелепіпед з сусідніми ребрами$L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)$, то обсяг$P$ дорівнює$|\operatorname{det}(M)|$.