1.1: Вступ до R

Обчислення - це вивчення функціональних взаємозв'язків і того, як пов'язані величини змінюються один з одним. Під час першого впливу на обчислення основна увага була зосереджена на функціях, що включають одну незалежну змінну та одну залежну змінну. Для$f,$ такої функції єдине вхідне дійсне число$x$ визначає унікальне єдине$f(x) .$ вихідне значення Однак багато функцій важливості як всередині самої математики, так і в застосуванні математики до решти світу включають багато змінних одночасно. Наприклад, часто у фізиці функція, яка описує силу, що діє на об'єкт, що рухається в просторі, залежить від трьох змінних, трьох координат яких описують розташування об'єкта. Якщо силова функція також змінюється з часом, то сила залежить від чотирьох змінних. Більш того, вихід силової функції сам буде включати три змінні, три координатні складові сили. Звідси сила функція така, що вона приймає три, або чотири, змінні для введення і виводить три змінні. Набагато складніші функції легко уявити: валовий національний продукт країни - це функція тисяч змінних з єдиною змінною як вихід, розклад авіакомпаній - це функція з тисячами входів (міста, літаки та люди, які плануються, а також інші змінні, такі як витрати на паливо. і графіки конкуруючих авіакомпаній) і, можливо, сотні виходів (конкретні маршрути пролетіли разом з їх часом). Хоча спочатку такі функції можуть виявитися набагато складнішими для роботи, ніж функції обчислення однієї змінної, ми побачимо, що часто ми зможемо звести проблеми, пов'язані з функціями декількох змінних, до пов'язаних проблем, що включають лише функції однієї змінної, проблеми, які ми можемо потім обробляти, використовуючи вже знайомі прийоми.

За визначенням функція приймає одне вхідне значення і пов'язує його з одним вихідним значенням. Отже, незважаючи на те, що в цій книзі входи до наших функцій часто будуть включати кілька змінних, як і виходи, ми все ж хочемо розглядати вхід і вихід функції як окремі точки в деякому багатовимірному просторі. Це природно у випадку, наприклад, описаної вище силової функції, де вхід є точкою в тривимірному просторі, чотири, якщо нам потрібно використовувати час, але вимагає деякої математичної абстракції, якщо ми хочемо розглядати вхід до функції валового національного продукту як точку в деякому просторі багатьох тисячі габаритів. Оскільки навіть геометрія двох і тривимірного простору може бути в деякому сенсі новою для вас, ми скористаємося цією главою для вивчення геометрії багатовимірного простору, перш ніж приступити до вивчення власне числення в главі 2.

По всій книзі ми дозволимо$\mathbb{R}$ позначити набір дійсних чисел.

Визначення: Евклідовий простір

Під n-мірним евклідовим простором ми маємо на увазі множину

$$\mathbb{R}^{n}=\left\{\left(x_{1}, x_{2}, \ldots, x_{n}\right): x_{i} \in \mathbb{R}, i=1,2, \ldots, n\right\}.$$

Тобто,$\mathbb{R}^{n}$ це простір всіх впорядкованих$n$ -кортежів дійсних чисел. Точку в цьому просторі ми позначимо

$$\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right),$$

і, бо$i=1,2, \ldots, n,$ ми$x_{i}$ називаємо$i$ й координату$\mathbf{x}$.

Приклад$\PageIndex{1}$

Коли у$n=2,$ нас є

$$\mathbb{R}^{2}=\left\{\left(x_{1}, x_{2}\right): x_{1}, x_{2} \in \mathbb{R}\right\},\nonumber$$

який є нашим знайомим поданням для точок у декартовій площині. Як завжди, в цьому випадку ми будемо часто позначати координати як$x$$y,$ і/або щось подібне, замість того, щоб нумерувати їх як$x_{1}$ і$x_{2}$.

Приклад$\PageIndex{2}$

Коли у$n=3,$ нас є

$$\mathrm{R}^{3}=\left\{\left(x_{1}, x_{2}, x_{3}\right): x_{1}, x_{2}, x_{3} \in \mathrm{R}\right\}.\nonumber$$

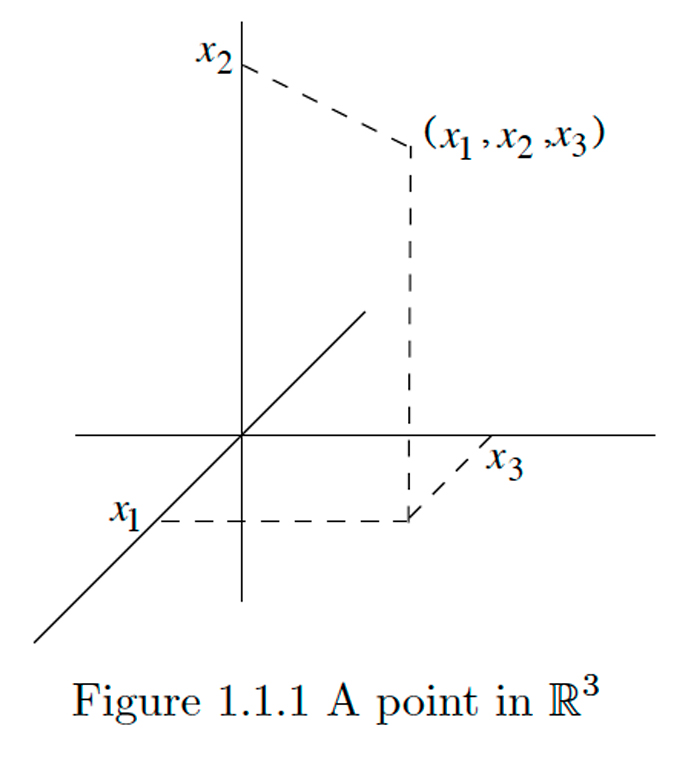
Подібно до того,$\mathbb{R}^{2}$ як ми можемо думати про спосіб присвоєння координат точкам на евклідовій площині, ми можемо думати про присвоєння координат тривимірному евклідовому простору.$\mathbb{R}^{3}$ Щоб зобразити цей простір, ми повинні уявити три взаємно перпендикулярні осі з координатами, позначеними вздовж осей, як на малюнку$1.1 .1 .$ Знову, ми часто будемо позначати координати точки в$\mathbb{R}^{3}$ як, наприклад,$x, y,$$u, v,$ і$z,$ або і$w,$ замість використання пронумеровані координати.

Приклад$\PageIndex{3}$

Якщо об'єкт рухається через простір, його розташування може бути вказано чотирма координатами, трьома просторовими координатами, скажімо,$x, y,$$z,$ і одноразовою координатою, скажімо$t$ Таким чином, його розташування визначається точкою$\mathbf{p}=(x, y, z, t)$ в$\mathbb{R}^{4} .$ Звичайно, ми не можемо намалювати картину такої точки.

Перед початком нашого геометричного вивчення$\mathbb{R}^{n},$ нам спочатку потрібно кілька основних алгебраїчних визначень.

Визначення

Дозволяти$\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ і$\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right)$ бути точки в$\mathbf{R}^{n}$ і нехай$a$ бути дійсним числом. Потім визначаємо

$$\mathbf{x}+\mathbf{y}=\left(x_{1}+y_{1}, x_{2}+y_{2}, \dots, x_{n}+y_{n}\right),$$

і

$$\mathbf{x}-\mathbf{y}=\left(x_{1}-y_{1}, x_{2}-y_{2}, \dots, x_{n}-y_{n}\right),$$

$$a \mathbf{x}=\left(a x_{1}, a x_{2}, \ldots, a x_{n}\right).$$

Приклад$\PageIndex{4}$

Якщо$x=(2,-3,1)$ і$y=(-4,1,-2)$ є двома пунктами,$R^{3},$ то

$$\begin{aligned} \mathbf{x}+\mathbf{y} &=(-2,-2,-1) \\ \mathbf{x}-\mathbf{y} &=(6,-4,3) \\ \mathbf{y}-\mathbf{x} &=(-6,4,-3) \\ 3 \mathbf{x} &=(6,-9,3), \end{aligned}$$

і

$$-2 y=(8,-2,4).\nonumber$$

Зверніть увагу, що ми визначили додавання і віднімання для точок в,$\mathbb{R}^{n},$ але ми не визначили множення. Взагалі немає форми множення для таких точок, яка корисна для нашої мети. Звичайно, множення визначається в особливому випадку$n=1$ і для особливого випадку,$n=2$ якщо розглядати точки в$\mathbb{R}^{2}$ як точки в комплексній площині. Ми побачимо в розділі 1.3, що є також цікавий і корисний тип множення в$\mathbb{R}^{3} .$ Також зауважте, що надає метод множення точки в$\mathbb{R}^{n}$ на$(1.1 .5)$ дійсне число, результатом якого є ще одна точка в$\mathrm{R}^{n}$. У таких випадках ми часто називаємо дійсне число скалярним і це множення скалярним множенням. Коротко наведемо геометричну інтерпретацію цієї форми множення.

Геометрія$\mathbb{R}^{n}$

Нагадаємо, що якщо$\mathbf{x}=\left(x_{1}, x_{2}\right)$ і$\mathbf{y}=\left(y_{1}, y_{2}\right)$ є двома точками,$\mathbb{R}^{2},$ то, використовуючи теорему Піфагора, відстань$\mathbf{y}$ від$\mathbf{x}$ до

$$\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}}.\nonumber$$

Ця формула легко узагальнюється до$\mathbb{R}^{3}:$ Припустимо$\mathbf{x}=\left(x_{1}, x_{2}, x_{3}\right)$ і$y=\left(y_{1}, y_{2}, y_{3}\right)$ є двома точками в$\mathrm{R}^{3} .$ Нехай$\mathbf{z}=\left(y_{1}, y_{2}, x_{3}\right) .$ Оскільки перші дві$\mathbf{z}$ координати$\mathbf{y}$ і однакові,$\mathbf{y}$ і$\mathbf{z}$ лежать на одній вертикальній лінії, і тому відстань між ними просто

$$\left|y_{3}-x_{3}\right|.$$

Причому,$x$ і$z$ мають однакову третю координату, і так лежать в одній горизонтальній площині. Звідси відстань між$\mathbf{x}$ і$\mathbf{z}$ таке ж, як і відстань між$\left(x_{1}, x_{2}\right)$ і$\left(y_{1}, y_{2}\right)$ в$\mathbb{R}^{2},$ тобто,

$$\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}}.\nonumber$$

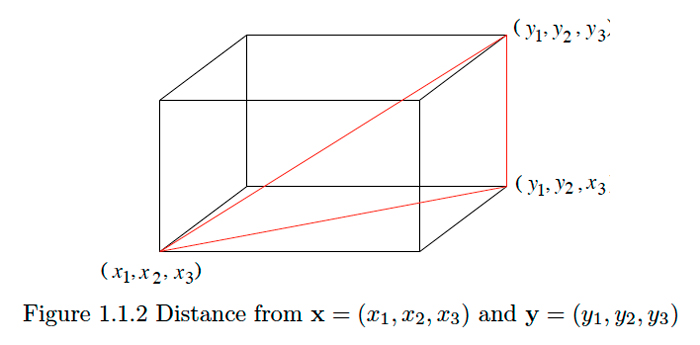
Нарешті, точки$\mathbf{x}, \mathbf{y},$ і$\mathbf{z}$ утворюють прямокутний трикутник з прямим кутом в$\mathbf{z} .$ Отже, використовуючи теорему Піфагора знову, відстань$y$ від$x$ до

$$\sqrt{(\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}})^{2}+\left|y_{3}-x_{3}\right|^{2}}=\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\left(y_{3}-x_{3}\right)^{2}}.\nonumber$$

Зокрема, якщо ми дозволимо$\|x \|$ позначити відстань від$x=\left(x_{1}, x_{2}, x_{3}\right)$ до початку$(0,0,0)$ в$\mathbb{R}^{3},$ то

$$\|\mathbf{x}\|=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}.\nonumber$$

При такому позначенні відстань від$\mathbf{x}$ до$\mathbf{y}$ дорівнює

$$\begin{aligned}\|\mathbf{y}-\mathbf{x}\| &=\left\|\left(y_{1}-x_{1}, y_{2}-x_{2}, y_{3}-x_{3}\right)\right\| \\ &=\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\left(y_{3}-x_{3}\right)^{2}} \end{aligned}$$

Приклад$\PageIndex{5}$

Якщо$x=(1,2,-3)$ і$y=(3,-2,1),$ тоді відстань від$x$ до початку

$$\|\mathbf{x}\|=\sqrt{1^{2}+2^{2}+(-3)^{2}}=\sqrt{14}\nonumber$$

і відстань від$x$ до$y$ задається

$$\|\mathbf{y}-\mathbf{x}\|=\|(2,-4,4)\|=\sqrt{4+16+16}=6.\nonumber$$

Хоча у нас немає ніяких фізичних аналогів, з якими можна працювати, коли$n>3,$ все ж ми можемо узагальнити$(1.1 .9)$, щоб визначити відстань в$\mathbb{R}^{n}$.

Визначення

Якщо$x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ є точкою в$\mathbb{R}^{n},$ ми визначаємо норму$x,$$\|\mathbf{x}\|,$ позначається

$$\|\mathbf{x}\|=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}}.\nonumber$$

Для двох точок$\mathbf{x}$ і$\mathbf{y}$ в$\mathbb{R}^{n},$ визначаємо відстань між$\mathbf{x}$ і$\mathbf{y},$ позначається$d(\mathbf{x}, \mathbf{y})$

від

$$d(\mathbf{x}, \mathbf{y})=\|\mathbf{y}-\mathbf{x}\|.\nonumber$$

Ми дозволимо$\mathbf{0}=(0,0, \ldots, 0)$ позначити походження в$\mathbb{R}^{n} .$ Тоді ми маємо

$$\|\mathbf{x}\|=d(\mathbf{x}, \mathbf{0});\nonumber$$

тобто нормою$x$ вважається відстань від$x$ до початку.

Приклад$\PageIndex{6}$

Якщо$x=(2,3,-1,5),$ точка в,$\mathbb{R}^{4},$ то відстань від$x$ до початку

$$\|\mathbf{x}\|=\sqrt{4+9+1+25}=\sqrt{39}.\nonumber$$

Якщо$\mathbf{y}=(3,2,1,4),$ тоді відстань від$\mathbf{x}$$\mathbf{y}$ до

$$d(\mathbf{x}, \mathbf{y})=\|\mathbf{y}-\mathbf{x}\|=\|(1,-1,2,-1)\|=\sqrt{7}.\nonumber$$

Зверніть увагу, що якщо$\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ є точкою в$\mathbb{R}^{n}$ і$a$ є скаляром, то

$$\begin{aligned} \|a \mathbf{x}\| &=\left\|\left(a x_{1}, a x_{2}, \ldots, a x_{n}\right)\right\| \\ &=\sqrt{a^{2} x_{1}^{2}+a^{2} x_{2}^{2}+\cdots+a^{2}x_{n}^{2}} \\ &=|a| \sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}} \\ &=|a|\|\mathbf{x}\|.\end{aligned}$$

Тобто, норма скалярного кратного$x$ - це всього лише абсолютне значення скалярного числа, що перевищує норму$\mathbf{x}$. Зокрема, якщо$\mathbf{x} \neq \mathbf{0},$ тоді

$$\left\|\frac{1}{\|\mathbf{x}\|} \mathbf{x}\right\|=\frac{1}{\|\mathbf{x}\|}\|\mathbf{x}\|=1.\nonumber$$

Тобто,

$$\frac{1}{\|\mathbf{x}\|} \mathbf{x}\nonumber$$

це одиниця відстані від початку.

Визначення

$\mathbf{p}=\left(p_{1}, p_{2}, \ldots, p_{n}\right)$Дозволяти бути точкою в$\mathbb{R}^{n}$ і нехай$r>0$ бути дійсним числом. Множина всіх точок,$\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ в$\mathbb{R}^{n}$ яких задовольняють рівняння

$$\left(x_{1}-p_{1}\right)^{2}+\left(x_{2}-p_{2}\right)^{2}+\cdots+\left(x_{n}-p_{n}\right)^{2}=r^{2}$$

називається$(n-1)-$ розмірна сфера з радіусом$r$ і центром,$\mathbf{p},$ яку ми позначимо$S^{n-1}(\mathbf{p}, r) .$ множиною всіх точок,$\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ в$\mathbb{R}^{n}$ яких задовольняють нерівність

$$\left(x_{1}-p_{1}\right)^{2}+\left(x_{2}-p_{2}\right)^{2}+\cdots+\left(x_{n}-p_{n}\right)^{2}<r^{2}$$

називається відкритим$n$ -мірним кулею з радіусом$r$ і центром$\mathbf{p},$ який ми позначимо$B^{n}(\mathbf{p}, r)$ множиною всіх точок,$\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ в$\mathbb{R}^{n}$ яких задовольняють нерівність

$$\left(x_{1}-p_{1}\right)^{2}+\left(x_{2}-p_{2}\right)^{2}+\cdots+\left(x_{n}-p_{n}\right)^{2} \leq r^{2}$$

називається замкнутим n-мірним кулею з радіусом$r$ і центром$\mathbf{P},$, який ми позначимо$\bar{B}^{n}(\mathbf{p}, r)$

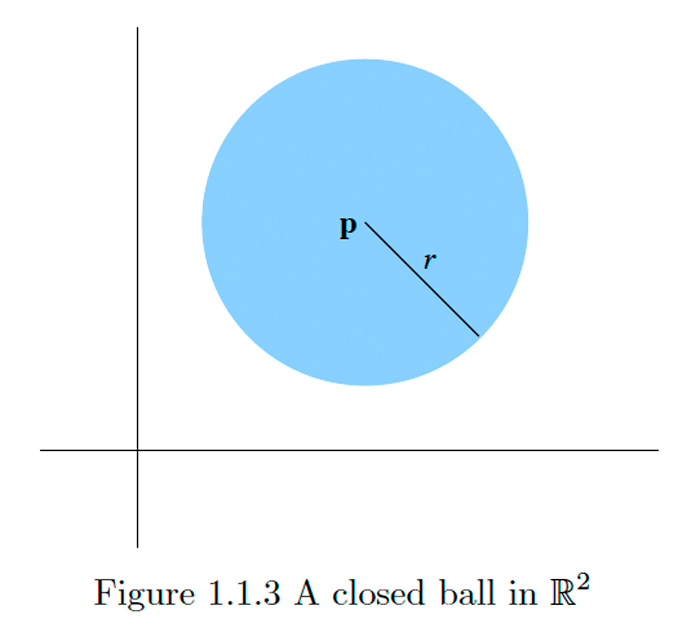
Сфера$S^{n-1}(\mathbf{p}, r)$ - це сукупність усіх точок, які лежать на фіксованій відстані$r$ від фіксованої точки$\mathbf{p}$ в$\mathbb{R}^{n}$. Зверніть увагу, що для$n=1, S^{0}(\mathbf{p}, r)$ складається тільки з двох точок, а саме, точка,$\mathbf{p}-r$ яка лежить на відстані$r$ зліва від$\mathbf{p}$ і точка$\mathbf{p}+r$, яка лежить на відстані$r$ праворуч від,$\mathbf{p} ; B^{1}(\mathbf{p}, r)$ є відкритим інтервалом$(\mathbf{p}-r, \mathbf{p}+r) ;$ і$\bar{B}^{1}(\mathbf{p}, r)$ є замкнутим інтервалом $[\mathbf{p}-r, \mathbf{p}+r] .$У цьому сенсі відкриті і закриті кулі є природними аналогами відкритих і замкнутих інтервалів на реальній лінії. Для$n=2,$ сфери - це коло, відкритий куля - це диск без його огороджувального кола, а замкнутий куля - диск разом з його огороджувальним колом.

Вектори

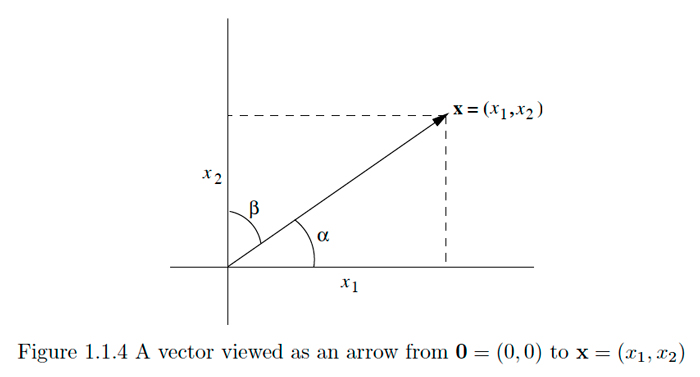
Багато величин, що цікавлять фізику, такі як швидкості, прискорення та сили, включають як величину, так і напрямок. Наприклад, ми можемо говорити про силу величини 10 ньютонів, що діють на об'єкт біля початку в площині під кутом$\frac{\pi}{4}$ з горизонталлю. Загальноприйнято зображувати таку величину, як стрілка, з довжиною, заданою величиною, і з кінчиком, спрямованим у вказаному напрямку, і називати її вектором 8. Тепер будь-яка точка$\mathbf{x}=\left(x_{1}, x_{2}\right), \mathbf{x} \neq \mathbf{0},$ в$\mathbb{R}^{2}$ визначає вектор в площині, а саме вектор, що починається з початку і закінчується на$\mathbf{x}$. Величина, або довжина, такого вектора є$\|\mathbf{x}\|$ і його напрямок задається кутом,$\alpha$ який він робить з горизонтальною віссю або кутом$\beta$, який він робить з вертикальною віссю. Зверніть увагу, що

$$\cos (\alpha)=\frac{x_{1}}{\|x\|}\nonumber$$

і

$$\cos (\beta)=\frac{x_{2}}{\|x\|}\nonumber$$

і що, хоча$\cos (\alpha)$ ні$\cos (\beta)$ однозначно не визначає напрямок вектора самостійно, разом вони повністю визначають напрямок. Див. Малюнок 1.1.4.

Загалом, ми можемо думати$\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ або як про точку в,$\mathbb{R}^{n}$ або як вектор,$\mathbb{R}^{n},$ починаючи з початку з довжини$\|\mathbf{x}\| .$ Якщо$\mathbf{x} \neq \mathbf{0},$ ми говоримо, за аналогією з випадком в

$\mathrm{R}^{2},$що напрямок$\mathrm{x}$ є вектором

$$\mathbf{u}=\left(\frac{x_{1}}{\|\mathbf{x}\|}, \frac{x_{2}}{\|\mathbf{x}\|}, \ldots, \frac{x_{n}}{\|\mathbf{x}\|}\right)\nonumber$$

Координати цього вектора$\mathbf{u}$ називаються косинусами напрямку,$\mathbf{x}$ тому що ми можемо думати про

$$u_{k}=\frac{x_{k}}{\|x\|} \nonumber$$

як косинус кута між вектором$x$ та$k$ й віссю для$k=1,2, \ldots, n,$ інтерпретації, яка стане зрозумілішою після нашого обговорення кутів$\mathbb{R}^{n}$ у наступному розділі. Крім того, ми можемо розглядати$\mathbf{u}$ як вектор одиничної довжини, який вказує в тому ж напрямку, що і$\mathbf{x}$. Будь-який вектор довжини,$1,$ такий як$\mathbf{u},$ називається одиничним вектором. Ми$\mathbf{0}$ називаємо нульовим вектором, оскільки він має довжину 0. Зверніть увагу, що 0 не має напрямку.

Приклад$\PageIndex{7}$

Вектор$\mathbf{x}=(1,2,-2,3)$ в$\mathbf{R}^{4}$ має довжину$\|\mathbf{x}\|=\sqrt{18}$ і напрямок

$$\mathbf{u}=\left(\frac{1}{\sqrt{18}}, \frac{2}{\sqrt{18}},-\frac{2}{\sqrt{18}}, \frac{3}{\sqrt{18}}\right)=\frac{1}{\sqrt{18}}(1,2,-2,3)\nonumber$$

Тепер можна надати геометричні значення нашим визначенням скалярного множення, додавання векторів та віднімання векторів. Спочатку зверніть увагу, що якщо$\mathbf{x} \neq \mathbf{0}$ і$a>0,$ потім

$$\|a \mathbf{x}\|=a\|\mathbf{x}\|,\nonumber$$

так що$\mathbf{x}$ має напрямок

$$\frac{1}{\|a \mathbf{x}\|} a \mathbf{x}=\frac{1}{\|\mathbf{x}\|} \mathbf{x}\nonumber$$

те ж саме, що і$\mathbf{x}$. Звідси$a \mathbf{x}$ вказує в тому ж напрямку, що і,$\mathbf{x},$ але з довжиною,$a$ помноженої на довжину$\mathbf{x} .$ Якщо,$a<0,$ то

$$\|a \mathbf{x}\|=|a|\|\mathbf{x}\|=-a\|\mathbf{x}\|,\nonumber$$

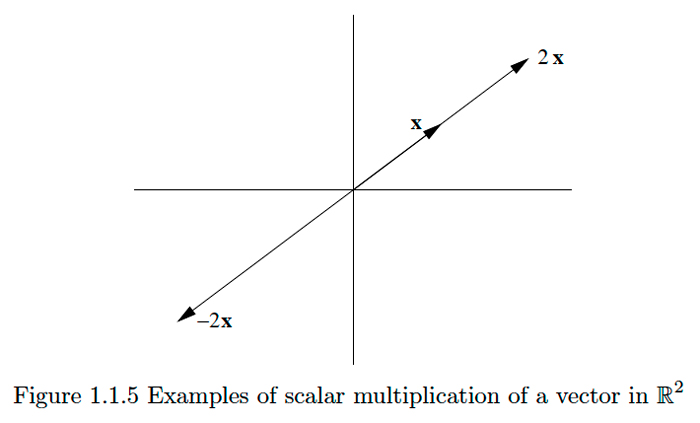
так$a x$ має напрямок

$$\frac{1}{\|a \mathbf{x}\|} a \mathbf{x}=-\frac{1}{\|\mathbf{x}\|} \mathbf{x}.\nonumber$$

Отже, в даному випадку$a x$ має протилежний напрямок$x$ з$|a|$ раз довжина х$\mathbb{R}^{2}$.
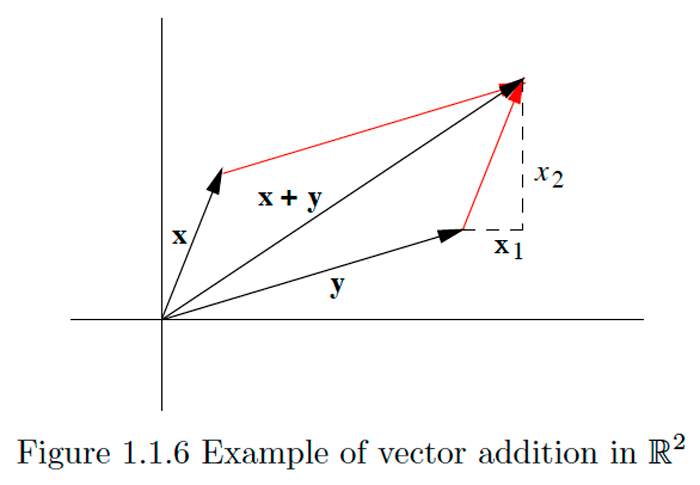
Далі розглянемо два вектори$\mathbf{x}=\left(x_{1}, x_{2}\right)$ і$\mathbf{y}=\left(y_{1}, y_{2}\right)$ in$\mathbb{R}^{2}$ та їх суму.
$$\mathbf{z}=\mathbf{x}+\mathbf{y}=\left(x_{1}+y_{1}, x_{2}+y_{2}\right).\nonumber$$

Зверніть увагу, що кінчик$\mathbf{z}$ знаходиться$x_{1}$ одиниць горизонтально і$x_{2}$ одиниць вертикально від кінчика$\mathbf{y} .$ Геометрично, кінчик$\mathbf{z}$ знаходиться на кінчику$\mathbf{x}$ якщо$\mathbf{x}$ були вперше перекладені паралельно собі так, що його хвіст тепер збігся з кінчиком $\mathbf{y} .$Аналогічно, ми можемо розглядати$\mathbf{z}$ як діагональ паралелограма, який має$\mathbf{x}$ і$\mathbf{y}$ для його сторін. Див. Рис. 1.1.6 для прикладу.

Нарешті, розглянемо два вектори$\mathbf{x}=\left(x_{1}, x_{2}\right)$ і$\mathbf{y}=\left(y_{1}, y_{2}\right)$ в$\mathbb{R}^{2}$ і їх відмінність

$$\mathbf{z}=\mathbf{x}-\mathbf{y}=\left(x_{1}-y_{1}, x_{2}-y_{2}\right).$$

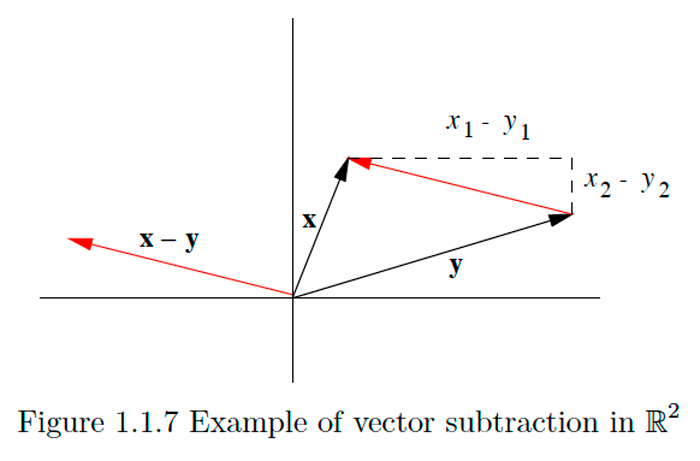
Зверніть увагу, що оскільки координати$\mathbf{z}$ є лише відмінностями в координатах$\mathbf{x}$ і$\mathbf{y}$,$\mathbf{z}$ має величину і напрямок стрілки, що вказує від кінчика$\mathbf{y}$ до кінчика$\mathbf{x}$, як показано на малюнку$1.1 .7 .$ Іншими словами, ми можемо зобразити $\mathbf{z}$геометрично, перекладаючи стрілку, намальовану від кінчика$\mathbf{y}$ до кінчика$\mathbf{z}$ паралельно собі, поки її хвіст не буде на початку.

У попередньому обговоренні це спокусливо думати про стрілку від кінчика$\mathbf{y}$ до кінчика$\mathbf{x}$ як насправді$\mathbf{x}-\mathbf{y},$ не просто паралельний переклад$\mathbf{x}-\mathbf{y} .$ Насправді, це зручно і корисно думати про паралельні переклади даного вектора, тобто вектори, які мають однаковий напрямок і величина, але з хвостами не біля початку, так як всі вони є одним і тим же вектором, просто намальовані в різних місцях простору. Ми побачимо багато випадків, коли перегляд векторів таким чином значно допомагає нашому розумінню.

Перш ніж закрити цей розділ, нам потрібно звернути увагу на деякі спеціальні вектори.

Визначення: Стандартні базисні вектори

Вектори

$$\begin{array}{l}{\mathbf{e}_{1}=(1,0,0, \ldots, 0)} \\ {\mathbf{e}_{2}=(0,1,0, \ldots, 0)} \\ {\vdots} \\ {\mathbf{e}_{n}=(0,0,0, \ldots, 1)}\end{array}$$

в$\mathbb{R}^{n}$ називаються стандартними базисними векторами.

Приклад$\PageIndex{8}$

У$\mathbb{R}^{2}$ стандартних базисних векторах є$\mathbf{e}_{1}=(1,0)$ і$\mathbf{e}_{2}=(0,1) .$ Зверніть увагу, що якщо$\mathbf{x}=(x, y)$ є який-небудь вектор в$\mathbb{R}^{2},$ то

$$\mathbf{x}=(x, 0)+(0, y)=x(1,0)+y(0,1)=x \mathbf{e}_{1}+y e_{2}. \nonumber$$

Наприклад,$(2,5)=2 \mathrm{e}_{1}+5 \mathrm{e}_{2}$.

Приклад$\PageIndex{9}$

У$\mathbb{R}^{3}$ стандартних базисних векторах є$\mathrm{e}_{1}=(1,0,0), \mathrm{e}_{2}=(0,1,0),$ і$\mathrm{e}_{3}=$$(0,0,1) .$ Зверніть увагу, що якщо$\mathbf{x}=(x, y, z)$ є який-небудь вектор в$\mathbb{R}^{3},$ то

$$\mathbf{x}=(x, 0,0)+(0, y, 0)+(0,0, z)=x(1,0,0)+y(0,1,0)+z(0,0,1)=x e_{1}+y e_{2}+z e_{3}\nonumber$$

Наприклад,$(1,2,-4)=\mathbf{e}_{1}+2 \mathbf{e}_{2}-4 \mathbf{e}_{3}$.

Попередні два приклади легко узагальнюються, щоб показати, що будь-який вектор в$\mathrm{R}^{n}$ може бути записаний як сума скалярних кратних стандартних базисних векторів. Зокрема, якщо$\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right),$ тоді ми можемо написати$\mathbf{x}$ як

$$\mathbf{x}=x_{1} \mathbf{e}_{1}+x_{2} \mathbf{e}_{2}+\cdots+x_{n} \mathbf{e}_{n}.$$

Ми говоримо, що$x$ це лінійна комбінація стандартних базисних векторів Також$e_{1}, e_{2}, \ldots, e_{n} .$ важливо відзначити, що існує лише один вибір для скалярів у цій лінійній комбінації. Тобто для будь-якого вектора$\mathbf{x}$ в$\mathbb{R}^{n}$ існує один і єдиний спосіб запису у$\mathbf{x}$ вигляді лінійної комбінації стандартних базисних векторів.

Примітки до позначення

У цьому тексті ми будемо позначати вектори, використовуючи звичайний жирний шрифт. Це загальна умовність, але не єдина, яка використовується для позначення векторів. Інша часто використовувана угода полягає в розміщенні стрілок над змінною, яка позначає вектор. Наприклад, можна написати$\vec{x}$ для того, що ми позначали$\mathbf{x}$.

Також варто відзначити, що у багатьох книгах стандартні базисні вектори в$\mathbb{R}^{2}$ позначаються i$\mathbf{j}(\text { or } \vec{i} \text { and } \vec{j}),$ і, а стандартні базисні вектори в$\mathbb{R}^{3}$ by$\mathbf{i}, \mathbf{j},$ і$\mathbf{k}$ (або$\vec{i}, \vec{j},$ і$\vec{k}$). Оскільки це позначення непросто розширити на більш високі розміри, ми не будемо багато використовувати його.