16.5: Розбіжність і завиток

Цілі навчання

• Визначте розбіжність за формулою для заданого векторного поля.
• Визначте локон за формулою для заданого векторного поля.
• Використовуйте властивості завивки і розбіжності, щоб визначити, чи є векторне поле консервативним.

У цьому розділі ми розглянемо дві важливі операції над векторним полем: дивергенція та завивка. Вони важливі для області числення з кількох причин, включаючи використання завитка та розбіжності для розробки деяких вищих версій фундаментальної теореми числення. Крім того, завиток і розбіжність з'являються в математичних описах механіки рідини, електромагнетизму та теорії пружності, які є важливими поняттями у фізиці та техніці. Ми також можемо застосувати завивку та розбіжність до інших понять, які ми вже досліджували. Наприклад, при певних умовах векторне поле консервативне тоді і тільки в тому випадку, якщо його завиток дорівнює нулю.

Окрім визначення завитків та розбіжностей, ми розглядаємо деякі фізичні інтерпретації їх та показуємо їх зв'язок із консервативними та безджерельними векторними полями.

Дивергенція

Дивергенція - це операція над векторним полем, яка повідомляє нам, як поле поводиться до точки або від неї. Локально розбіжність векторного поля$\vecs{F}$ в певній точці$\mathbb{R}^2$ або$\mathbb{R}^3$ в конкретній точці$P$ є мірою «відтоку» векторного поля при$P$. Якщо$\vecs{F}$ являє собою швидкість рідини, то розбіжність$\vecs{F}$ at$P$ вимірює чисту швидкість зміни по відношенню до часу кількості рідини, що стікає з$P$ (схильність рідини до витікання «з» Р). Зокрема, якщо кількість рідини, що надходить, збігається$P$ з кількістю, що витікає назовні, то розбіжність при$P$ дорівнює нулю.

Визначення: розбіжність в$\mathbb{R}^3$

Якщо$\vecs{F} = \langle P,Q,R \rangle$ є векторним полем в$\mathbb{R}^3$$P_x, \, Q_y,$ і$R_z$ все існує, то розбіжність$\vecs{F}$ визначається

$$\begin{align} \text{div}\, F &= P_x + Q_y + R_z \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}. \end{align} \nonumber$$

Зверніть увагу, що розбіжність векторного поля - це не векторне поле, а скалярна функція. З точки зору оператора градієнта

$$\vecs \nabla = \langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \rangle \nonumber$$

дивергенція може бути записана символічно як точковий добуток

$$\text{div}\, \vecs F = \vecs \nabla \cdot \vecs{F}. \nonumber$$

Зауважте, що це просто корисне позначення, оскільки точковий добуток вектора операторів та вектора функцій не визначено осмислено, враховуючи наше поточне визначення точкового добутку.

Якщо$\vecs{F} = \langle P,Q \rangle$ є векторним полем в$\mathbb{R}^2$,$P_x$ і$Q_y$ обидва існують, то розбіжність$\vecs{F}$ визначається аналогічно як

$$\begin{align*} \text{div}\, \vecs{F} &= P_x + Q_y \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} \\[4pt] &= \vecs \nabla \cdot \vecs{F}. \end{align*}$$

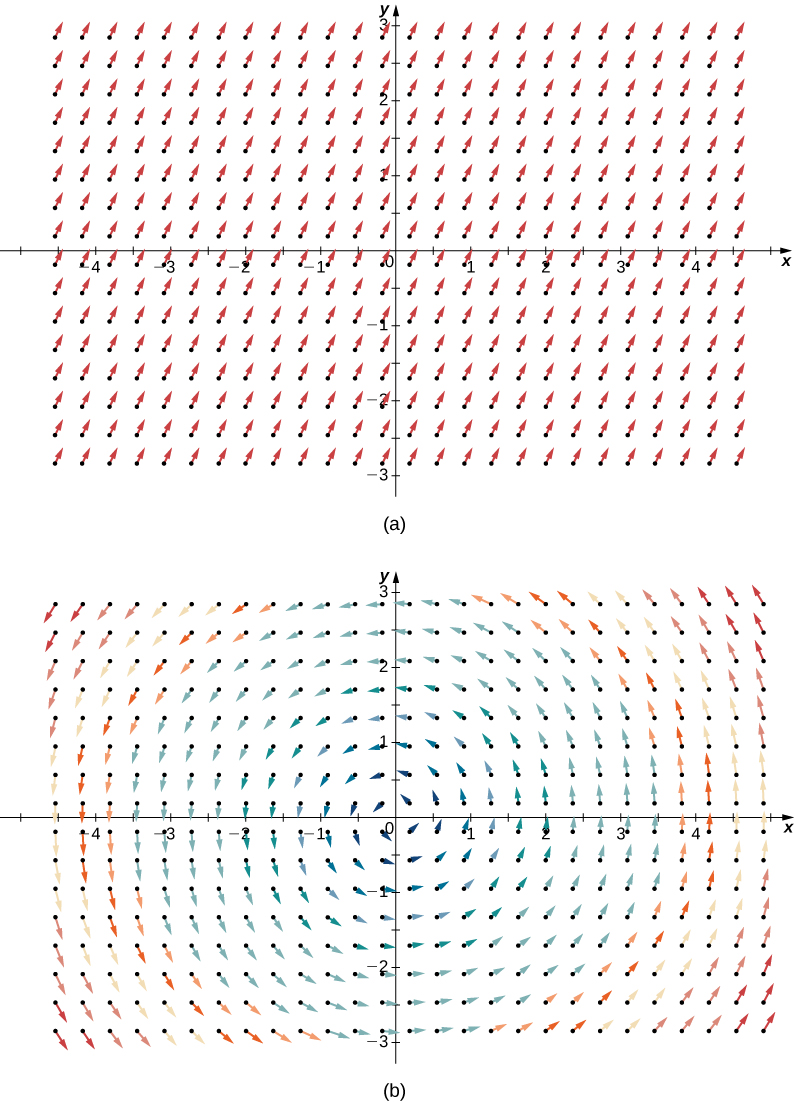
Щоб проілюструвати цей момент, розглянемо два векторних поля на малюнку$\PageIndex{1}$. У будь-якій конкретній точці сума, що протікає, така ж, як і сума, що витікає, тому в кожній точці «витікання» поля дорівнює нулю. Тому ми очікуємо, що розбіжність обох полів буде нульовою, і це дійсно так, як

$$\text{div}(\langle 1,2 \rangle ) = \dfrac{\partial}{\partial x} (1) + \dfrac{\partial}{\partial y}(2) = 0 \nonumber$$

і

$$\text{div}(\langle -y,x \rangle ) = \dfrac{\partial}{\partial x} (-y) + \dfrac{\partial}{\partial y} (x) = 0. \nonumber$$

Рисунок$\PageIndex{1}$: (a)$\langle 1,2 \rangle$ Векторне поле має нульову розбіжність. (b) Векторне поле$\langle -y,x \rangle$ також має нульову розбіжність.

На відміну від цього, розглянемо радіальне векторне поле$\vecs{R} (x,y) = \langle -x, -y \rangle$ на малюнку$\PageIndex{2}$. У будь-якій точці тече більше рідини, ніж витікає назовні, і тому «відходження» поля негативна. Ми очікуємо, що розбіжність цього поля буде негативною, і це дійсно так, як

$$\text{div}(\vecs{R}) = \dfrac{\partial}{\partial x} (-x) + \dfrac{\partial}{\partial y} (-y) = -2. \nonumber$$

Малюнок$\PageIndex{2}$: Це векторне поле має негативну дивергенцію.

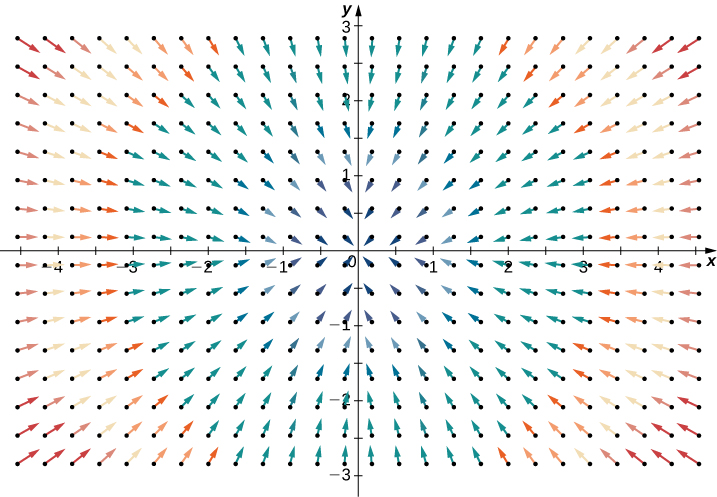
Щоб отримати глобальне відчуття того, що розбіжність говорить нам, припустимо, що векторне поле в$\mathbb{R}^2$ являє собою швидкість рідини. Уявіть собі, як взяти пружне коло (коло з формою, яку можна змінити векторним полем) і скинути його в рідину. Якщо коло зберігає свою точну площу в міру протікання через рідину, то розбіжність дорівнює нулю. Це сталося б для обох векторних полів на малюнку$\PageIndex{1}$. З іншого боку, якщо форма кола спотворюється так, що його площа зменшується або розширюється, то розбіжність не дорівнює нулю. Уявіть собі падіння такого пружного кола в радіальне векторне поле на малюнку$\PageIndex{2}$ так, щоб центр кола приземлився в точці$(3, 3)$. Коло текло б до початку, і як це робилося, передня частина кола рухатиметься повільніше, ніж задня, внаслідок чого коло «подряпається» і втрачає площу. Ось так можна побачити негативну розбіжність.

Приклад$\PageIndex{1}$: Calculating Divergence at a Point

Якщо$\vecs{F}(x,y,z) = e^x \hat{i} + yz \hat{j} - yz^2 \hat{k}$, то знайдіть розбіжність$\vecs{F}$ в$(0,2,-1)$.

Рішення

Розбіжність$\vecs{F}$ є

$$\dfrac{\partial}{\partial x} (e^x) + \dfrac{\partial}{\partial y}(yz) - \dfrac{\partial}{\partial z} (y z^2) = e^x + z - 2yz. \nonumber$$

Тому розбіжність при$(0,2,-1)$ є$e^0 - 1 + 4 = 4$. Якщо$\vecs{F}$ являє собою швидкість рідини, то більше рідини витікає, ніж протікає в точці$(0,2,-1)$.

Вправа$\PageIndex{1}$

Знайти$\text{div}\, \vecs{F}$ для

$$\vecs{F}(x,y,z) = \langle xy, \, 5-z^2, \, x^2 + y^2 \rangle \nonumber. \nonumber$$

Підказка

Дотримуйтесь приклад$\PageIndex{1}$.

Відповідь

$\text{div}\, \vecs{F} = y$

Одне застосування для розбіжності відбувається в фізиці, при роботі з магнітними полями. Магнітне поле - це векторне поле, яке моделює вплив електричних струмів і магнітних матеріалів. Фізики використовують розбіжність в законі Гаусса для магнетизму, який стверджує, що якщо$\vecs{B}$ це магнітне поле, то$\vecs \nabla \cdot \vecs{B} = 0$; іншими словами, розбіжність магнітного поля дорівнює нулю.

Приклад$\PageIndex{2}$: Determining Whether a Field Is Magnetic

Чи можливо бути магнітним полем?$\vecs{F} (x,y) = \langle x^2 y, \, y - xy^2 \rangle$

Рішення

Якби$\vecs{F}$ були магнітні, то його розбіжність дорівнювала б нулю. Розбіжність$\vecs{F}$ є

$$\dfrac{\partial}{\partial x} (x^2y) + \dfrac{\partial}{\partial y} (y - xy^2) = 2 xy + 1 - 2 xy = 1 \nonumber$$

і тому$\vecs{F}$ не може моделювати магнітне поле (рис.$\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Розбіжність векторного поля$\vecs{F} (x,y) = \langle x^2 y, \, y - xy^2 \rangle$ одна, тому вона не може моделювати магнітне поле.

Ще одним додатком для розбіжності є виявлення того, чи поле є джерелом вільного. Нагадаємо, що поле без джерела - це векторне поле, яке має функцію потоку; еквівалентно, вільне від джерела поле - це поле з потоком, який дорівнює нулю вздовж будь-якої замкнутої кривої. Наступні дві теореми говорять про те, що за певних умов безджерельні векторні поля є саме векторними полями з нульовою розбіжністю.

Теорема: Розбіжність векторного поля, вільного від джерела

Якщо$\vecs{F} = \langle P,Q \rangle$ є безджерельним неперервним векторним полем з диференційованими компонентними функціями, то$\text{div}\, \vecs{F} = 0$.

Доказ

Так$\vecs{F}$ як джерело вільний, є функція$g(x,y)$ з$g_y = P$ і$-g_x = Q$. Тому$\vecs{F} = \langle g_y, -g_x \rangle$ і$\text{div}\, \vecs{F} = g_{yx} - g_{xy} = 0$ по теоремі Клеро.

$\square$

Конверс розбіжності векторного поля без джерела вірно для просто пов'язаних регіонів, але доказ є занадто технічним, щоб включити сюди. Таким чином, ми маємо наступну теорему, яка може перевірити, чи$\mathbb{R}^2$ є векторне поле в джерелі вільним.

Теорема: Тест на розбіжність для векторних полів без джерел

$\vecs{F} = \langle P,Q \rangle$Дозволяти безперервне векторне поле з диференційованими компонентними функціями з областю, яка просто пов'язана. Тоді,$\text{div}\, \vecs{F} = 0$ якщо і тільки$\vecs{F}$ якщо джерело вільний.

Приклад$\PageIndex{3}$: Determining Whether a Field Is Source Free

Чи вільне$\vecs{F} (x,y) = \langle x^2 y, \, 5 - xy^2 \rangle$ джерело поля?

Рішення

Зверніть увагу на домен$\vecs{F}$ є$\mathbb{R}^2$, який просто підключений. Крім того,$\vecs{F}$ є безперервним з диференційованими компонентними функціями. Тому ми можемо використовувати тест на розбіжність для векторних полів без джерел для аналізу$\vecs{F}$. Розбіжність$\vecs{F}$ є

$$\dfrac{\partial}{\partial x} (x^2 y) + \dfrac{\partial}{\partial y} (5 - xy^2 ) = 2xy - 2xy = 0. \nonumber$$

Таким чином,$\vecs{F}$ джерело вільний від тесту на дивергенцію для векторних полів без джерела.

Вправа$\PageIndex{2}$

$\vecs{F} (x,y) = \langle -ay, bx \rangle$Дозволяти обертальне поле де$a$ і$b$ є додатними константами. Чи є$\vecs{F}$ джерело безкоштовним?

Підказка

Обчисліть розбіжність.

Відповідь

Так

Нагадаємо, що форма потоку теореми Гріна говорить про те, що

$$\oint_C \vecs F \cdot \vecs N \; ds = \iint_D P_x + Q_y \;dA, \nonumber$$

де$C$ проста замкнута$D$ крива і область, обведена$C$. Оскільки$P_x + Q_y = \text{div}\,\vecs F$ теорема Гріна іноді пишеться як

$$\oint_C \vecs F \cdot \vecs N\; ds = \iint_D \text{div}\, \vecs F \;dA. \nonumber$$

Тому теорему Гріна можна записати з точки зору розбіжності. Якщо розглядати дивергенцію як похідну роду, то теорема$\vecs{F}$ Гріна говорить, що «похідна» від області може бути переведена в лінійний інтеграл$\vecs{F}$ вздовж межі області. Це аналогічно фундаментальній теоремі числення, в якій похідна функції$f$ на відрізку прямої$[a,b]$ може бути переведена в твердження про$f$ на межі$[a,b]$. Використовуючи дивергенцію, ми можемо побачити, що теорема Гріна є вищим аналогом фундаментальної теореми числення.

Ми можемо використовувати все те, що ми дізналися, у застосуванні розбіжності. $\vecs{v}$Дозволяти векторне поле моделювання швидкості рідини. Оскільки розбіжність$\vecs{v}$ в точці$P$ вимірює «відтік» рідини в$P$,$\text{div}\, v(P) > 0$ означає, що більше рідини витікає з,$P$ ніж протікає всередину. Аналогічно,$\text{div}\, v(P) < 0$ має на увазі, що більше рідини тече в,$P$ ніж витікає, і$\text{div}\, \vecs{v}(P) = 0$ означає, що така ж кількість рідини протікає, як витікає.

Приклад$\PageIndex{4}$: Determining Flow of a Fluid

Припустимо$\vecs{v}(x,y) = \langle -xy,y \rangle, \, y > 0$ моделює потік рідини. Чи більше рідини тече в точку$(1,4)$, ніж витікає назовні?

Рішення

Щоб визначити, чи стікає більше рідини,$(1,4)$ ніж витікає назовні, обчислюємо розбіжність$\vecs v$ при$(1,4)$:

$$div(\vecs{v}) = \dfrac{\partial}{\partial x} (-xy) + \dfrac{\partial}{\partial y} (y) = -y + 1. \nonumber$$

Щоб знайти розбіжність в$(1,4)$ підставте точку на розбіжність:$-4 + 1 = -3$. Оскільки розбіжність$\vecs v$ at$(1,4)$ негативна, більше рідини тече, ніж витікає назовні (рис.$\PageIndex{4}$).

Малюнок$\PageIndex{4}$:$\vecs{v}(x,y) = \langle -xy, y \rangle$ Векторне поле має негативну дивергенцію$(1,4)$

Вправа$\PageIndex{3}$

Для векторного поля знайти всі точки$\vecs{v}(x,y) = \langle -xy, y \rangle , \, y > 0$,$P$ такі, що кількість рідини, що протікає в$P$ дорівнює кількості рідини, що витікає з$P$.

Підказка

Знайдіть, де розбіжність дорівнює нулю.

Відповідь

Всі точки на лінії$y = 1$.

завиток

Друга операція над векторним полем, яку ми досліджуємо, - це завиток, який вимірює ступінь обертання поля навколо точки. Припустимо, що$\vecs{F}$ представляє поле швидкості рідини. Потім завиток$\vecs{F}$ точки$P$ - це вектор, який вимірює тенденцію частинок поблизу$P$ обертатися навколо осі, яка вказує у напрямку цього вектора. Величина вектора завитка при$P$ вимірює, наскільки швидко частинки обертаються навколо цієї осі. Іншими словами, завиток у точці є мірою «спина» векторного поля в цій точці. Візуально уявіть собі розміщення веслового колеса в рідину на$P$, з віссю веслового колеса вирівняною з вектором завитка (рис.$\PageIndex{5}$). Завиток вимірює тенденцію обертання веслового колеса.

Малюнок$\PageIndex{5}$: Щоб візуалізувати завиток у точці, уявіть, що в точці розміщено невелике весло у векторному полі.

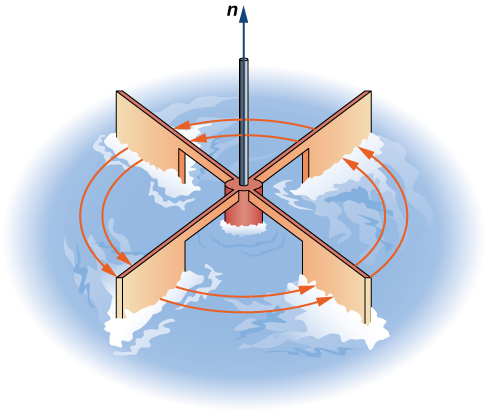
Розглянемо векторні поля на малюнку$\PageIndex{1}$. У частині (а) векторне поле є постійним і немає спина в будь-якій точці. Тому ми очікуємо, що завиток поля буде дорівнює нулю, і це дійсно так. Частина (b) показує обертальне поле, тому поле має спін. Зокрема, якщо ви поміщаєте веслове колесо в поле в будь-якій точці так, щоб вісь колеса була перпендикулярна площині, колесо обертається проти годинникової стрілки. Тому ми очікуємо, що завиток поля буде ненульовим, і це дійсно так (завиток є$2\,\mathbf{\hat k}$).

Щоб побачити, який локон вимірює глобально, уявіть, як скинути лист у рідину. Коли лист рухається разом з потоком рідини, завиток вимірює тенденцію листа до обертання. Якщо завиток дорівнює нулю, то лист не обертається, коли рухається через рідину.

Визначення: Curl

Якщо$\vecs{F} = \langle P,Q,R \rangle$ є векторним полем в$\mathbb{R}^3$$P_x, \, Q_y$, і, і$R_z$ все існує, то завивка$\vecs{F}$ визначається

\ [\ почати {вирівняти}\ текст {завиток}\,\ vecs {F} &= (R_y - Q_z)\,\ mathbf {\ капелюх я} + (p_z - r_x)\,\ mathbf {\ капелюх j} + (Q_x - p_y)\,\ mathbf {\ капелюх k}\ [4pt]
&=\ лівий (\ dfrac {\ частковий R} {\ частковий y} -\ dfrac {\ частковий Q} {\ частковий z}\ правий)\,\ mathbf {\ hat i} +\ лівий (\ dfrac {\ частковий P} {\ частковий z} -\ dfrac {\ частковий R} {\ частковий х}\ право)\,\ mathbf {\ hat j} +\ лівий (\ dfrac {\ частковий Q} {\ частковий х} -\ dfrac {\ частковий P} {\ частковий y}\ праворуч)\,\ mathbf {\ hat k}. \ end {вирівняти}\ nonumber\]

Зверніть увагу, що завиток векторного поля є векторним полем, на відміну від розбіжності.

Визначення локона буває складно запам'ятати. Щоб допомогти у запам'ятовуванні, ми використовуємо позначення$\vecs \nabla \times \vecs{F}$ для позначення «визначника», який дає формулу локонів:

$$\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber$$

Визначником цієї матриці є

$$(R_y - Q_z) \,\mathbf{\hat i} - (R_x - P_z) \,\mathbf{\hat j} + (Q_x - P_y) \,\mathbf{\hat k} = (R_y - Q_z) \,\mathbf{\hat i} + (P_z - R_x) \,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} = \text{curl}\, \vecs{F}. \nonumber$$

Таким чином, дана матриця - спосіб допомогти запам'ятати формулу для завивки. Майте на увазі, однак, що слово детермінант використовується дуже вільно. Детермінант насправді не визначено на матриці з записами, які є трьома векторами, трьома операторами та трьома функціями.

Якщо$\vecs{F} = \langle P,Q \rangle$ є векторним полем в$\mathbb{R}^2$, то завиток$\vecs{F}$, за визначенням, є

$$\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right)\,\mathbf{\hat k}. \nonumber$$

Приклад$\PageIndex{5}$: Finding the Curl of a Three-Dimensional Vector Field

Знайдіть локон$\vecs{F}(P,Q,R) = \langle x^2 z, e^y + xz, xyz \rangle$.

Рішення

Завиток - це

$$\begin{align*} \text{curl}\, f &= \vecs\nabla \times \vecs{F} \\ &= \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \partial/\partial x & \partial/\partial y & \partial / \partial z \\ P & Q & R \end{vmatrix} \\ &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\ &= (xz - x)\,\mathbf{\hat i} + (x^2 - yz)\,\mathbf{\hat j} + z \,\mathbf{\hat k}. \end{align*}$$

Вправа$\PageIndex{4}$

Знайдіть завиток$\vecs{F} = \langle \sin x \, \cos z, \, \sin y \, \sin z, \, \cos x \, \cos y \rangle$ в точці$\left(0, \dfrac{\pi}{2}, \dfrac{\pi}{2} \right)$.

Підказка

Знайдіть детермінант матриці$\vecs \nabla \times \vecs{F}$.

Відповідь

$-\hat{i}$

Приклад$\PageIndex{6}$: Finding the Curl of a Two-Dimensional Vector Field

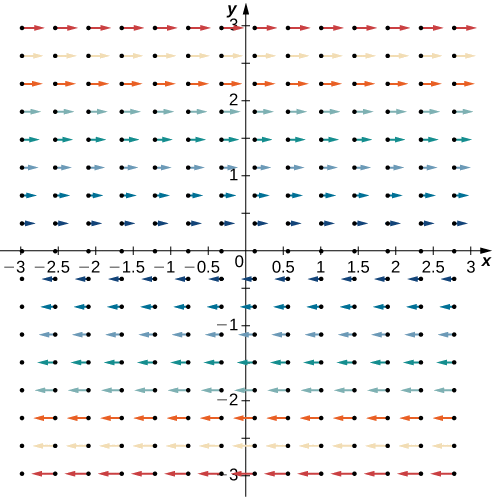
Знайдіть локон$\vecs{F} = \langle P,Q \rangle = \langle y,0\rangle$.

Рішення

Зверніть увагу, що це векторне поле складається з векторів, які всі паралельні. По суті, кожен вектор в полі паралельний осі x. Цей факт може привести нас до висновку, що поле не має спина і що локон дорівнює нулю. Щоб перевірити цю теорію, зауважте, що

$$\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = -\,\mathbf{\hat k} \neq \vecs 0. \nonumber$$

Таким чином, це векторне поле дійсно має спін. Щоб зрозуміти чому, уявіть собі розміщення веслового колеса в будь-якій точці першого квадранта (рис.$\PageIndex{6}$). Більші величини векторів у верхній частині колеса змушують колесо обертатися. Колесо обертається за годинниковою стрілкою (негативним) напрямком, викликаючи негативний коефіцієнт завитка.

Малюнок$\PageIndex{6}$: Векторне поле$\vecs{F}(x,y) = \langle y,0\rangle$ складається з векторів, які всі паралельні.

Зверніть увагу, що якщо$\vecs{F} = \langle P,Q\rangle$ є векторним полем в площині, то$\text{curl}\, \vecs{F} \cdot \mathbf{\hat k} = (Q_x - P_y)\,\mathbf{\hat k} \cdot \mathbf{\hat k} = Q_x - P_y$. Тому циркуляційна форма теореми Гріна іноді записується як

$$\oint_C \vecs{F} \cdot d\vecs{r} = \iint_D \text{curl}\, \vecs F \cdot \,\mathbf{\hat k}\,dA, \nonumber$$

де$C$ проста замкнута$D$ крива і область, обведена$C$. Тому циркуляційну форму теореми Гріна можна записати в терміні завитка. Якщо розглядати curl як похідну роду, то теорема$\vecs{F}$ Гріна говорить, що «похідна» від області може бути переведена в лінійний інтеграл$\vecs{F}$ вздовж межі області. Це аналогічно фундаментальній теоремі числення, в якій похідна функції$f$ на відрізку прямої$[a,b]$ може бути переведена в твердження про$f$ на межі$[a,b]$. Використовуючи curl, ми можемо побачити циркуляційну форму теореми Гріна є більш вимірним аналогом фундаментальної теореми обчислення.

Тепер ми можемо використовувати те, що ми дізналися про завиток, щоб показати, що гравітаційні поля не мають «спина». Припустимо, що на початку є об'єкт з масою$m_1$ в початку і об'єкт з масою$m_2$. Нагадаємо, що гравітаційна сила, яку об'єкт 1 чинить на об'єкт 2, задається полем.

$$\vecs{F}(x,y,z) = - Gm_1m_2 \left\langle \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\right\rangle. \nonumber$$

Приклад$\PageIndex{7}$: Determining the Spin of a Gravitational Field

Покажіть, що гравітаційне поле не має спина.

Рішення

Щоб показати, що не$\vecs{F}$ має прядки, обчислюємо його локон. Нехай

• $P(x,y,z) = \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}$,
• $Q(x,y,z) = \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}$, і
• $R(x,y,z) = \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}$.

Потім,

\ [\ почати {вирівнювати*}\ текст {завиток}\,\ vecs {F} &= - GM_1m_2 [(R_y - q_z)\ mathbf {\ капелюх я} + (p_z - r_x)\ mathbf {\ капелюх j} + (Q_x - p_y)\ mathbf {\ капелюх k}\ [4pt]
&= - GM_1m_2\ почати {pmatrix}\ ліворуч (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}} -\ ліворуч (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}}\ праворуч\) математика {\ капелюх я}\ номер\\ [4pt]
+\ лівий (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}} -\ вліво (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}}\ праворуч)\ mathbf {\ капелюх j}\ номер\\ [4pt]
+\ ліворуч (\ dfrac {-3xy} {(x^2 + y^2 + z^2) ^ {5/2}} -\ ліворуч (\ dfrac {-3xy} {(x^2+ y^2 + z^2) ^ {5/2}}\ праворуч)\ праворуч)\ mathbf {\ капелюх k}\ кінець {pmatrix}\\ [4pt]
&=\ векс 0. \ end {вирівнювати*}\]

Так як завиток гравітаційного поля дорівнює нулю, то поле не має спина.

Вправа$\PageIndex{7}$

Поле$\vecs{v}(x,y) = \langle - \dfrac{y}{x^2+y^2}, \dfrac{x}{x^2+y^2} \rangle$ моделює потік рідини. Покажіть, що якщо ви опускаєте лист в цю рідину, як лист рухається з часом, лист не обертається.

Підказка

Розрахуйте локон.

Відповідь

$\text{curl}\, \vecs{v} = \vecs 0$

Використання дивергенції та завитка

Тепер, коли ми розбираємося в основних поняттях дивергенції і завивки, ми можемо обговорити їх властивості і встановити зв'язки між ними і консервативними векторними полями.

Якщо$\vecs{F}$ є векторним полем,$\mathbb{R}^3$ то завиток також$\vecs{F}$ є векторним полем в$\mathbb{R}^3$. Тому можна взяти розбіжність локона. Наступна теорема говорить, що результат завжди дорівнює нулю. Цей результат корисний, оскільки дає нам можливість показати, що деякі векторні поля не є завитком будь-якого іншого поля. Щоб дати цьому результату фізичну інтерпретацію, нагадаємо, що розбіжність поля$\vecs{v}$ швидкості в точці$P$ вимірює тенденцію відповідної рідини до витікання$P$. Так як$\text{div}(\text{curl}\,\vecs v) = 0$, чиста швидкість потоку в векторному полі в$\text{curl}\;\vecs v$ будь-якій точці дорівнює нулю. Прийняття завитка векторного поля$\vecs{F}$ усуває будь-які розбіжності, які були присутні в$\vecs{F}$.

Теорема: Розбіжність завитка

$\vecs{F} = \langle P,Q,R \rangle$Дозволяти векторне поле в$\mathbb{R}^3$ такому, що компонентні функції всі мають неперервні часткові похідні другого порядку. Потім,

$$\text{div}(\text{curl}\, \vecs{F}) = \vecs\nabla \cdot (\vecs \nabla \times \vecs F) = 0. \nonumber$$

Доказ

За визначеннями дивергенції і завитка, і за теоремою Клеро,

$$\begin{align*} \text{div}(\text{curl}\, \vecs{F}) = \text{div}[(R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k}] \\ = R_{yx} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy}\\ = 0. \end{align*}$$

$\Box$

Приклад$\PageIndex{8}$: Showing That a Vector Field Is Not the Curl of Another

Покажіть, що$\vecs{F}(x,y,z) = e^x\,\mathbf{\hat i}+ yz\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}$ це не завиток іншого векторного поля. Тобто показати, що іншого вектора$\vecs{G}$ с немає$\text{curl} \, \vecs G = \vecs F$.

Рішення

Зверніть увагу, що домен$\vecs{F}$ є все з$\mathbb{R}^3$ і другого порядку$\vecs{F}$ частки всі безперервні. Тому ми можемо застосувати попередню теорему до$\vecs{F}$.

Розбіжність$\vecs{F}$ є$e^x + z + 2xz$. $\vecs{F}$Якби були завиток векторного поля$\vecs{G}$, то$\text{div}\, \vecs F = \text{div}(\text{curl} \,\vecs G) = 0$. Але, розбіжність не$\vecs{F}$ дорівнює нулю, а тому не$\vecs{F}$ є завитком будь-якого іншого векторного поля.

Вправа$\PageIndex{8}$

Чи можна бути$\vecs G(x,y,z) = \langle \sin x, \, \cos y, \, \sin (xyz)\rangle$ завитком векторного поля?

Підказка

Знайдіть розбіжність$\vecs{G}$.

Відповідь

Ні.

Наступними двома теоремами ми покажемо, що якщо$\vecs{F}$ є консервативним векторним полем, то його завиток дорівнює нулю, а якщо область просто пов'язана, то зворотне також вірно.$\vecs{F}$ Це дає нам ще один спосіб перевірити, чи є векторне поле консервативним.

Теорема: Завиток консервативного векторного поля

Якщо$\vecs{F} = \langle P,Q,R\rangle$ консервативний, то$\text{curl} \, \vecs{F} = \vecs 0$.

Доказ

Оскільки консервативні векторні поля задовольняють властивість cross-partials, всі перехресні частки$\vecs F$ є рівними. Тому,

$$\begin{align*} \text{curl}\, \vecs{F} &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\[4pt] &= \vecs 0. \end{align*}$$

$\Box$

Та ж теорема вірна і для векторних полів у площині.

Оскільки консервативне векторне поле є градієнтом скалярної функції, попередня теорема говорить, що$\text{curl}\, (\vecs \nabla f) = \vecs 0$ для будь-якої скалярної функції$f$. З точки зору нашого позначення локонів,$\vecs \nabla \times \vecs \nabla (f) = \vecs 0$. Це рівняння має сенс, оскільки перехресний добуток вектора з самим собою завжди є нульовим вектором. Іноді$\vecs \nabla \times \vecs \nabla (f) = \vecs 0$ рівняння спрощується як$\vecs \nabla \times \vecs \nabla = \vecs 0$.

Теорема: Тест на завиток для консервативного поля

$\vecs{F} = \langle P,Q,R\rangle$Дозволяти бути векторне поле в просторі на просто підключений домен. Якщо$\text{curl}\;\vecs F = \vecs 0$,$\vecs{F}$ то консервативний.

Доказ

З тих пір$\text{curl}\, \vecs F = \vecs 0$, у нас є що$R_y = Q_z, \, P_z = R_x$, і$Q_x = P_y$. Тому$\vecs{F}$ задовольняє властивість крос-partials на просто пов'язаному домені, а крос-часткова властивість консервативних полів передбачає, що$\vecs{F}$ це консервативне.

$\Box$

Та ж теорема вірна і в площині. Тому якщо$\vecs{F}$ векторне поле в площині або в просторі і область просто пов'язана,$\vecs{F}$ то консервативна якщо і тільки якщо$\text{curl}\, \vecs F = \vecs 0$.

Приклад$\PageIndex{9}$: Testing Whether a Vector Field Is Conservative

Використовуйте локон, щоб визначити,$\vecs{F}(x,y,z) = \langle yz, xz, xy\rangle$ консервативний чи.

Рішення

Зверніть увагу, що домен$\vecs{F}$ - це все з$\mathbb{R}^3$ яких просто підключено (рис.$\PageIndex{7}$). Тому ми можемо перевірити, чи$\vecs{F}$ консервативний, розрахувавши його локон.

Малюнок$\PageIndex{7}$: Завиток векторного поля$\vecs{F}(x,y,z) = \langle yz, xz, xy\rangle$ дорівнює нулю.

Завиток$\vecs{F}$ є

$$\left(\dfrac{\partial}{\partial y}xy - \dfrac{\partial}{\partial z} xz \right) \,\mathbf{\hat i} + \left(\dfrac{\partial}{\partial y}yz - \dfrac{\partial}{\partial z} xy \right) \,\mathbf{\hat j} + \left(\dfrac{\partial}{\partial y}xz - \dfrac{\partial}{\partial z} yz \right)\,\mathbf{\hat k}= (x - x)\,\mathbf{\hat i} + (y - y)\,\mathbf{\hat j} + (z - z)\,\mathbf{\hat k} = \vecs 0. \nonumber$$

Таким чином,$\vecs{F}$ є консервативним.

Ми бачили, що завиток градієнта дорівнює нулю. Що таке розбіжність градієнта? Якщо$f$ є функцією двох змінних, то$\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy}$. Ми скорочуємо цей «подвійний крапковий добуток» як$\vecs \nabla^2$. Цей оператор називається оператором Лапласа, і в цьому позначенні стає рівняння Лапласа$\vecs \nabla^2 f = 0$. Тому гармонічна функція - це функція, яка стає нулем після прийняття розбіжності градієнта.

Аналогічно, якщо$f$ є функцією трьох змінних, то

$$\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy} + f_{zz}. \nonumber$$

Використовуючи ці позначення, ми отримуємо рівняння Лапласа для гармонійних функцій трьох змінних:

$$\vecs \nabla^2 f = 0. \nonumber$$

Гармонічні функції виникають у багатьох додатках. Наприклад, потенційна функція електростатичного поля в області простору, яка не має статичного заряду, є гармонійною.

Приклад$\PageIndex{10}$: Finding a Potential Function

Чи можлива потенційна функція електростатичного поля, яке знаходиться в області$\mathbb{R}^2$ вільної від статичного заряду?$f(x,y) = x^2 + x - y$

Рішення

$f$Якби була така потенційна функція, то$f$ була б гармонійною. Зверніть увагу, що$f_{xx} = 2$ і$f_{yy} = 0$, і так$f_{xx} + f_{yy} \neq 0$. Тому не$f$ є гармонійним і$f$ не може представляти електростатичний потенціал.

Вправа$\PageIndex{10}$

Чи можливо функція$f(x,y) = x^2 - y^2 + x$ бути потенційною функцією електростатичного поля, розташованого в області$\mathbb{R}^2$ без статичного заряду?

Підказка

Визначте, чи є функція гармонійною.

Відповідь

Так.

Ключові концепції

• Розбіжність векторного поля є скалярною функцією. Дивергенція вимірює «відтік» векторного поля. Якщо$\vecs{v}$ поле швидкості рідини, то розбіжність$\vecs{v}$ в точці - це відтік рідини менше припливу в точці.
• Завиток векторного поля є векторним полем. Завиток векторного поля в точці$P$ вимірює тенденцію частинок при$P$ обертанні навколо осі, яка вказує у напрямку завитка на$P$.
• Векторне поле з просто пов'язаним доменом консервативне тоді і тільки тоді, коли його завиток дорівнює нулю.

Ключові рівняння

• завиток

$$\vecs \nabla \times \vecs{F} = (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \nonumber$$

• Дивергенція

$$\vecs \nabla \cdot \vecs{F} = P_x + Q_y + R_z\nonumber$$

• Розбіжність завитка дорівнює нулю

$$\vecs \nabla \cdot (\vecs \nabla \times \vecs F) = 0\nonumber$$

• Завиток градієнта - нульовий вектор

$$\vecs \nabla \times (\vecs \nabla f) = 0 \nonumber$$

Глосарій

завиток

завиток векторного поля$\vecs{F}=⟨P,Q,R⟩$,$\vecs ∇× \vecs{F}$ що позначається є «визначником» матриці $$\begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber$$ і задається виразом$(R_y−Q_z)\,\mathbf{\hat i} +(P_z−R_x)\,\mathbf{\hat j} +(Q_x−P_y)\,\mathbf{\hat k}$; він вимірює тенденцію частинок в точці до обертання навколо осі, яка вказує в напрямку завитка в точці

розбіжність

розбіжність векторного поля$\vecs{F}=⟨P,Q,R⟩$, що позначається$\vecs ∇× \vecs{F}$, є$P_x+Q_y+R_z$; він вимірює «відтікання» векторного поля