13.2: Обчислення векторно-значних функцій

Цілі навчання

• Напишіть вираз для похідної векторно-значної функції.
• Знайти тангенс вектор в точці для заданого вектора позиції.
• Знайдіть одиничний тангенс вектора в точці для заданого вектора положення і поясніть його значення.
• Обчисліть певний інтеграл векторно-значної функції.

Для вивчення числення векторно-значних функцій ми слідуємо аналогічним шляхом до того, який ми взяли при вивченні дійсних функцій. Спочатку визначаємо похідну, потім вивчаємо додатки похідної, потім переходимо до визначення інтегралів. Однак ми знайдемо кілька цікавих нових ідей на цьому шляху в результаті векторної природи цих функцій та властивостей космічних кривих.

Похідні векторно-значних функцій

Тепер, коли ми побачили, що таке векторно-значна функція і як взяти її межу, наступним кроком є вивчення того, як диференціювати векторну функцію. Визначення похідної векторно-значної функції майже ідентично визначенню дійсної функції однієї змінної. Однак, оскільки діапазон векторно-значної функції складається з векторів, те саме справедливо і для діапазону похідної векторно-значної функції.

Означення: Похідна векторно-значних функцій

Похідна векторно-значної функції\(\vecs{r}(t)\) дорівнює

\[\vecs{r}′(t) = \lim \limits_{\Delta t \to 0} \dfrac{\vecs{r}(t+\Delta t)−\vecs{r}(t)}{ \Delta t} \label{eq1} \]

за умови, що ліміт існує. Якщо\(\vecs{r}'(t)\) існує, то\(\vecs{r}(t)\) диференціюється при\(t\). Якщо\(\vecs{r}′(t)\) існує для всіх\(t\) у відкритому інтервалі,\((a,b)\) то\(\vecs{r}(t)\) диференціюється за інтервал\((a,b)\). Щоб функція була диференційованою протягом замкнутого інтервалу\([a,b]\), також повинні існувати наступні дві межі:

\[\vecs{r}′(a) = \lim \limits_{\Delta t \to 0^+} \dfrac{\vecs{r}(a+\Delta t)−\vecs{r}(a)}{ \Delta t} \nonumber \]

і

\[\vecs{r}′(b) = \lim \limits_{\Delta t \to 0^-} \dfrac{\vecs{r}(b+\Delta t)−\vecs{r}(b)}{ \Delta t} \nonumber \]

Багато правил обчислення похідних дійсних функцій можуть бути застосовані і для обчислення похідних векторно-значних функцій. Нагадаємо, що похідна від дійснозначної функції може бути інтерпретована як нахил дотичної лінії або миттєва швидкість зміни функції. Похідну векторно-значної функції також можна розуміти як миттєву швидкість зміни; наприклад, коли функція представляє положення об'єкта в даний момент часу, похідна представляє його швидкість в той самий момент часу.

Зараз ми продемонструємо взяття похідної від векторно-значної функції.

Приклад\(\PageIndex{1}\): Finding the Derivative of a Vector-Valued Function

Використовуйте визначення для обчислення похідної функції

\[\vecs{r}(t)=(3t+4) \,\mathbf{\hat{i}}+(t^2−4t+3) \,\mathbf{\hat{j}} .\nonumber \]

Рішення

Давайте використаємо рівняння\ ref {eq1}:

\ [\ почати {вирівнювати*}\ vecs {r} ′ (t) &=\ lim\ limits_ {\ Дельта t\ до 0}\ dfrac {\ vecs {r} (t+Δt) −\ vecs {r} (t)} {Δt}\ [4pt]
&=\ lim\ limits_ {\ Дельта t\ до 0}\ dfrac {[(3 (T+Δt) +4)\,\ hat {\ mathbf {i}} + ((T+Δt) ^2−4 (T+Δt) +3)\,\ hat {\ mathbf {j}}] − [(3т+4)\,\ капелюх {\ mathbf {i}} + (t^2−4t+3)\,\ капелюх {\ mathbf {i}} + (t^2−4t+3)\,\ капелюх {\ mathbf {i}} {\ mathbf {j}}]} {Δt}\\ [4 pt]
&=\ lim\ limits_ {\ дельта t\ до 0}\ dfrac {(3t+3Δt+4)\,\ hat {\ mathbf {i}} − (3t+4)\,\ hat {\ mathbf {i}} + (T^2+2TΔt+ (Δt) ^2−4T−4Δt+3)\ капелюх {\ mathbf {j}} − (t^2−4t+3)\,\ hat {\ mathbf {j}}} {Δt}\ [4pt]
&=\ lim\ limits_ {\ дельта t\ до 0}\ dfrac {(3Δt)\,\ капелюх {\ mathbf {i}} + (2TΔt+ (Δt) ^2−4Δt)\,\ капелюх {\ mathbf {j}}} {Δt}\\ [4pt]
&=\ lim\ limits_ {\ дельта t\ до 0} (3\,\ hat {\ mathbf {i}} + (2t+Δt−4)\,\ капелюх {\ mathbf {j}})\\ [4pt]
&=3\,\ капелюх {\ mathbf {j}} f {i}} + (2t−4)\,\ hat {\ mathbf {j}}\ end {align*}\ nonumber\]

Вправа\(\PageIndex{1}\)

Використовуйте визначення для обчислення похідної функції\(\vecs{r}(t)=(2t^2+3) \,\mathbf{\hat{i}}+(5t−6) \,\mathbf{\hat{j}}\).

Підказка

Використовуйте рівняння\ ref {eq1}.

Відповідь

\[\vecs{r}′(t)=4t \,\mathbf{\hat{i}}+5 \,\mathbf{\hat{j}} \nonumber \]

Зверніть увагу, що в розрахунках у прикладі\(\PageIndex{1}\), ми також могли б отримати відповідь, спочатку обчисливши похідну кожної компонентної функції, а потім повернувши ці похідні назад у векторну функцію. Це завжди вірно для обчислення похідної векторно-значної функції, незалежно від того, чи є вона в двох або трьох вимірах. Ми стверджуємо це в наступній теоремі. Доказ цієї теореми випливає безпосередньо з визначень межі векторно-значної функції та похідної векторно-значної функції.

Теорема\(\PageIndex{1}\): Differentiation of Vector-Valued Functions

Дозволяти\(f\)\(g\), і\(h\) бути диференційованими функціями\(t\).

1. Якщо\(\vecs{r}(t)=f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}}\) тоді\[\vecs{r}′(t)=f′(t) \,\mathbf{\hat{i}}+g′(t) \,\mathbf{\hat{j}}. \nonumber \]
2. Якщо\(\vecs{r}(t)=f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}\) тоді\[\vecs{r}′(t)=f′(t) \,\mathbf{\hat{i}}+g′(t) \,\mathbf{\hat{j}} + h′(t) \,\mathbf{\hat{k}}. \nonumber \]

Приклад\(\PageIndex{2}\): Calculating the Derivative of Vector-Valued Functions

Використовуйте\(\PageIndex{1}\) теорему для обчислення похідної кожної з наступних функцій.

1. \(\vecs{r}(t)=(6t+8) \,\mathbf{\hat{i}}+(4t^2+2t−3) \,\mathbf{\hat{j}}\)
2. \(\vecs{r}(t)=3 \cos t \,\mathbf{\hat{i}}+4 \sin t \,\mathbf{\hat{j}}\)
3. \(\vecs{r}(t)=e^t \sin t \,\mathbf{\hat{i}}+e^t \cos t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\)

Рішення

Використовується теорема\(\PageIndex{1}\) і те, що ми знаємо про диференціювання функцій однієї змінної.

1. Першою складовою\[\vecs r(t)=(6t+8) \,\mathbf{\hat{i}}+(4t^2+2t−3) \,\mathbf{\hat{j}} \nonumber \] є\(f(t)=6t+8\). Друга складова - це\(g(t)=4t^2+2t−3\). У нас є\(f′(t)=6\) і\(g′(t)=8t+2\), так Теорема\(\PageIndex{1}\) дає\(\vecs r′(t)=6 \,\mathbf{\hat{i}}+(8t+2)\,\mathbf{\hat{j}}\).
2. Перший компонент - це,\(f(t)=3 \cos t\) а другий компонент -\(g(t)=4 \sin t\). У нас є\(f′(t)=−3 \sin t\) і\(g′(t)=4 \cos t\), таким чином, отримуємо\(\vecs r′(t)=−3 \sin t \,\mathbf{\hat{i}}+4 \cos t \,\mathbf{\hat{j}}\).
3. Перший компонент\(\vecs r(t)=e^t \sin t \,\mathbf{\hat{i}}+e^t \cos t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\) є\(f(t)=e^t \sin t\), другий компонент є\(g(t)=e^t \cos t\), а третій компонент є\(h(t)=−e^{2t}\). У нас є\(f′(t)=e^t(\sin t+\cos t)\)\(g′(t)=e^t (\cos t−\sin t)\), і\(h′(t)=−2e^{2t}\), так теорема дає\(\vecs r′(t)=e^t(\sin t+\cos t)\,\mathbf{\hat{i}}+e^t(\cos t−\sin t)\,\mathbf{\hat{j}}−2e^{2t} \,\mathbf{\hat{k}}\).

Вправа\(\PageIndex{2}\)

Обчислити похідну функції

\[\vecs{r}(t)=(t \ln t)\,\mathbf{\hat{i}}+(5e^t) \,\mathbf{\hat{j}}+(\cos t−\sin t) \,\mathbf{\hat{k}}. \nonumber \]

Підказка

Визначте компонентні функції та використовуйте теорему\(\PageIndex{1}\).

Відповідь

\[\vecs{r}′(t)=(1+ \ln t) \,\mathbf{\hat{i}}+5e^t \,\mathbf{\hat{j}}−(\sin t+\cos t)\,\mathbf{\hat{k}} \nonumber \]

Ми можемо розширити до векторних функцій властивості похідної, яку ми представили раніше. Зокрема, постійне кратне правило, правила суми та різниці, правило добутку та правило ланцюга поширюються на векторні функції. Однак у випадку з правилом продукту насправді існує три розширення:

1. для дійсної функції, помноженої на векторну функцію,
2. для крапкового добутку двох векторно-значних функцій, і
3. для перехресного добутку двох векторних функцій.

Теорема: Властивості похідної векторно-значних функцій

\(\vecs{r}\)\(\vecs{u}\)Дозволяти і бути диференційовні векторно-значні функції\(t\),\(f\) нехай диференційовна дійсно-значна функція\(t\), і нехай\(c\) бути скалярною.

\[\begin{array}{lrcll} \mathrm{i.} & \dfrac{d}{\,dt}[c\vecs r(t)] & = & c\vecs r′(t) & \text{Scalar multiple} \nonumber\\ \mathrm{ii.} & \dfrac{d}{\,dt}[\vecs r(t)±\vecs u(t)] & = & \vecs r′(t)±\vecs u′(t) & \text{Sum and difference} \nonumber\\ \mathrm{iii.} & \dfrac{d}{\,dt}[f(t)\vecs u(t)] & = & f′(t)\vecs u(t)+f(t)\vecs u′(t) & \text{Scalar product} \nonumber\\ \mathrm{iv.} & \dfrac{d}{\,dt}[\vecs r(t)⋅\vecs u(t)] & = & \vecs r′(t)⋅\vecs u(t)+\vecs r(t)⋅\vecs u′(t) & \text{Dot product} \nonumber\\ \mathrm{v.} & \dfrac{d}{\,dt}[\vecs r(t)×\vecs u(t)] & = & \vecs r′(t)×\vecs u(t)+\vecs r(t)×\vecs u′(t) & \text{Cross product} \nonumber\\ \mathrm{vi.} & \dfrac{d}{\,dt}[\vecs r(f(t))] & = & \vecs r′(f(t))⋅f′(t) & \text{Chain rule} \nonumber\\ \mathrm{vii.} & \text{If} \; \vecs r(t)·\vecs r(t) & = & c, \text{then} \; \vecs r(t)⋅\vecs r′(t) \; =0 \; . & \mathrm{} \nonumber \end{array} \nonumber \]

Доказ

Докази перших двох властивостей випливають безпосередньо з визначення похідної векторно-значної функції. Третя властивість може бути виведена з перших двох властивостей разом з правилом продукту. Нехай\(\vecs u(t)=g(t)\,\mathbf{\hat{i}}+h(t)\,\mathbf{\hat{j}}\). Тоді

\ [\ почати {вирівнювати*}\ dfrac {d} {\, DT} [f (t)\ vecs u (t)] &=\ dfrac {d} {\, dt} [f (t) (g (t)\,\ mathbf {\ mathbf {\ mathbf {\ mathbf {j}}]\ [4pt]
&=\ dfrac {d} {\, DT} [f (t) г (т)\,\ mathbf {\ hat {i}} +f (t) h (t)\,\ mathbf {\ капелюх {j}}]\\ [4pt]
&=\ dfrac {d} {\ dt} [f (t) г (т) г (т)]\,\ mathbf {\ hat {i}} +\ dfrac {d} {\, DT} [f (t) h (t)]\,\ mathbf {\ hat {j}}\\ [4pt]
&= (f′ (t) г (т) +f (t) g′ (t)))\,\ mathbf {\ hat {i}} + (f′ (t) h (t) +f (t) h′ (t) h (t) h (t) h (t) mathbf {\ hat {j}}\\ [4pt]
&=f′ (t)\ vecs u (t) +f (t)\ vecs u′ (t). \ end {вирівнювати*}\ nonumber\]

Довести майно iv. нехай\(\vecs r(t)=f_1(t) \,\mathbf{\hat{i}}+g_1(t) \,\mathbf{\hat{j}}\) і\(\vecs u(t)=f_2(t) \,\mathbf{\hat{i}}+g_2(t) \,\mathbf{\hat{j}}\). Тоді

\ [\ почати {align*}\ dfrac {d} {\, DT} [\ векс r (t) ⋅\ векс u (t)] &=\ dfrac {d} {\, dt} [f_1 (t) f_2 (t) +g_1 (t) g_2 (t)]\\ [4pt]
&=f_1′ (t) _2 (т) +f_1 (t) f_2′ (t) +g_1′ (t) г_2 (т) +g_1 (t) g_2′ (t) =f_1′ (t) f_2 (t) +g_1′ (t) g_2 (t) г_2 (т) +f_1 (t) f_2′ (т) +г_1 (т) t) g_2′ (t)\\ [4pt]
& = (f_1′\,\ mathbf {\ капелюх {я}} +g_1′\,\ mathbf {\ капелюх {j}}) ⋅ (f_2\,\ mathbf {\ капелюх {i}} +g_2\,\ mathbf {\ капелюх {j}}) + (f_1\,\ mathbf {\ капелюх {я}} +g_1\,\ mathbf {\ капелюх {j}}}) ⋅ (f_2′\,\ mathbf thbf {\ hat {i}} +g_2′\,\ mathbf {\ hat {j}})\\ [4pt]
&=\ векс r′ (t) ⋅\ векс u (t) +\ vecs r (t) ⋅\ векс u (t). \ end {вирівнювати*}\ nonumber\]

Доказ власності v. Подібний до майна iv. Властивість vi. можна довести за допомогою правила ланцюга. Останнє, властивість vii. випливає з майна iv:

\ [\ почати {вирівнювати*}\ dfrac {d} {\, DT} [\ vecs r (t) ·\ векс r (t)] &=\ dfrac {d} {\, dt} [c]\ [4pt]
\ vecs r′ (t) ·\ векс r (t) +\ vecs r (t) ·\ vecs r′ (t) = 0\\ [4pt]
2\ векс r (t) ·\ векс r′ (t) &= 0\\ [4pt]
\ векс r (t) ·\ векс r′ (t) &= 0\ кінець {вирівнювати*}\ nonumber\]

Тепер для деяких прикладів використання цих властивостей.

Приклад\(\PageIndex{3}\): Using the Properties of Derivatives of Vector-Valued Functions

Задано векторно-значні функції

\[\vecs{r}(t)=(6t+8)\,\mathbf{\hat{i}}+(4t^2+2t−3)\,\mathbf{\hat{j}}+5t \,\mathbf{\hat{k}} \nonumber \]

і

\[\vecs{u}(t)=(t^2−3)\,\mathbf{\hat{i}}+(2t+4)\,\mathbf{\hat{j}}+(t^3−3t)\,\mathbf{\hat{k}}, \nonumber \]

обчислити кожну з наступних похідних, використовуючи властивості похідної векторно-значних функцій.

1. \(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{u}(t)]\)
2. \(\dfrac{d}{\,dt}[ \vecs{u} (t) \times \vecs{u}′(t)]\)

Рішення

У нас є\(\vecs{r}′(t)=6 \,\mathbf{\hat{i}}+(8t+2) \,\mathbf{\hat{j}}+5 \,\mathbf{\hat{k}}\) і\(\vecs{u}′(t)=2t \,\mathbf{\hat{i}}+2 \,\mathbf{\hat{j}}+(3t^2−3) \,\mathbf{\hat{k}}\). Тому відповідно до майна iv:

1. \ [\ почати {вирівнювати*}\ dfrac {d} {\, DT} [\ векс r (t) ⋅\ векс u (t)] &=\ векс r′ (t) ⋅\ векс u (t) +\ векс r (t) ⋅\ векс u (t)\\ [4pt]
   &= (6\,\ mathbf {\ hat {}} + (8т+2)\,\ mathbf {\ hat {j}} +5\,\ mathbf {\ капелюх {k}}) ⋅ ((t^2−3)\,\ mathbf {\ капелюх {i}} + (2т+4)\,\ mathbf {\ капелюх {j}} + (t^3−3t)\,\ mathbf {\ шапка {j}} + (t^3−3t)\,\ mathbf thbf {\ капелюх {k}})\\ [4pt]
   &\; + ((6т+8)\,\ mathbf {\ капелюх {i}} + (4t^2+2t−3)\,\ mathbf {\ капелюх {j}} +5t\,\ mathbf {\ капелюх {k}}) ⋅ (2t\,\ mathbf {\ капелюх {я}} +2\,\ mathbf {\ капелюх {j}} + (3t^2−3)\,\ mathbf {\ капелюх {k}})\\ [4pt]
   &= 6 (t^2−3) + (8т+2) (2т+4) +5 (t^3−3t)\\ [4pt]
   &\; +2t (6т+8) +2 (4т^2−3)) +5т (3т^2−3)\\ [4пт ]
   &= 20т^3+42т^2+26т−16. \ end {вирівнювати*}\]
2. По-перше, нам потрібно адаптувати властивість v для цієї проблеми:

   \[\dfrac{d}{\,dt}[ \vecs{u}(t) \times \vecs{u}′(t)]=\vecs{u}′(t)\times \vecs{u}′(t)+ \vecs{u}(t) \times \vecs{u}′′(t). \nonumber \]

   Нагадаємо, що перехресний добуток будь-якого вектора з самим собою дорівнює нулю. Крім того,\(\vecs u′′(t)\) являє собою другу похідну від\(\vecs u(t):\)

   \[\vecs u′′(t)=\dfrac{d}{\,dt}[\vecs u′(t)]=\dfrac{d}{\,dt}[2t \,\mathbf{\hat{i}}+2 \,\mathbf{\hat{j}}+(3t^2−3) \,\mathbf{\hat{k}}]=2 \,\mathbf{\hat{i}}+6t \,\mathbf{\hat{k}}. \nonumber \]

   Тому,

   \ [\ почати {вирівнювати*}\ dfrac {d} {\, DT} [\ vecs u (t)\ раз\ векс u′ (t)] &=0+ ((t^2−3)\,\ hat {\ mathbf {i}} + (2t+4)\,\ капелюх {\ mathbf {j}} + (t^3−t)\,\ капелюх {\ mathbf {k}})\ раз (2\,\ капелюх {\ mathbf {i}} +6t\,\ капелюх {\ mathbf {k}})\ [4pt]
   &=\ почати {vmatrix}\,\ капелюх {\ mathbf {я}} &\,\ капелюх {\ mathbf {j} &\,\ капелюх {\ mathbf {k}}\\ t^2-3 & 2t+4 & t^3 -3t\\ 2 & 0 & 6t\ кінець {vmatrix}\\ [4pt]
   & =6t (2т+4)\,\ hat {\ mathbf {i}} − (6t (t^2−3) −2 (t^3−3t))\,\ капелюх {\ mathbf {j}} −2 (2т+4)\,\ капелюх {\ mathbf {k}}\\ [4pt]
   & =( 12t^2+24t)\,\ капелюх {\ mathbf {i}} + (12t−4t^3)\,\ капелюх {\ mathbf {j}}} − (4т+8)\, \ капелюх {\ mathbf {k}}. \ end {вирівнювати*}\]

Вправа\(\PageIndex{3}\)

Обчислити\(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{r}′(t)]\) і\( \dfrac{d}{\,dt}[\vecs{u}(t) \times \vecs{r}(t)]\) для векторних функцій:

• \(\vecs{r}(t)=\cos t \,\mathbf{\hat{i}}+ \sin t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\)
• \(\vecs{u}(t)=t \,\mathbf{\hat{i}}+ \sin t \,\mathbf{\hat{j}}+ \cos t \,\mathbf{\hat{k}}\),

Підказка

Виконайте ті ж дії, що і в прикладі\(\PageIndex{3}\).

Відповідь

\(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{r}′(t)]=8e^{4t}\)

\( \dfrac{d}{\,dt}[ \vecs{u}(t) \times \vecs{r}(t)] =−(e^{2t}(\cos t+2 \sin t)+ \cos 2t) \,\mathbf{\hat{i}}+(e^{2t}(2t+1)− \sin 2t) \,\mathbf{\hat{j}}+(t \cos t+ \sin t− \cos 2t) \,\mathbf{\hat{k}}\)

Дотичні вектори та одиничні дотичні вектори

Нагадаємо, що похідна в точці може бути інтерпретована як нахил дотичної лінії до графіка в цій точці. У випадку векторнозначної функції похідна забезпечує дотичний вектор до кривої, представленої функцією. Розглянемо векторно-значну функцію

\[\vecs{r}(t)=\cos t \,\mathbf{\hat{i}} + \sin t \,\mathbf{\hat{j}} \label{eq10} \]

Похідна цієї функції

\[\vecs{r}′(t)=−\sin t \,\mathbf{\hat{i}} + \cos t \,\mathbf{\hat{j}} \nonumber \]

Якщо підставити значення\(t=π/6\) в обидві функції, ми отримаємо

\[\vecs{r} \left(\dfrac{π}{6}\right)=\dfrac{\sqrt{3}}{2} \,\mathbf{\hat{i}}+\dfrac{1}{2}\,\mathbf{\hat{j}} \nonumber \]

і

\[ \vecs{r}′ \left(\dfrac{π}{6} \right)=−\dfrac{1}{2}\,\mathbf{\hat{i}}+\dfrac{\sqrt{3}}{2}\,\mathbf{\hat{j}}. \nonumber \]

Графік цієї функції відображається на рисунку\(\PageIndex{1}\) разом з векторами\(\vecs{r}\left(\dfrac{π}{6}\right)\) і\(\vecs{r}' \left(\dfrac{π}{6}\right)\).

Малюнок\(\PageIndex{1}\): Дотична лінія в точці обчислюється з похідної векторно-значної функції\(\vecs{r}(t)\).

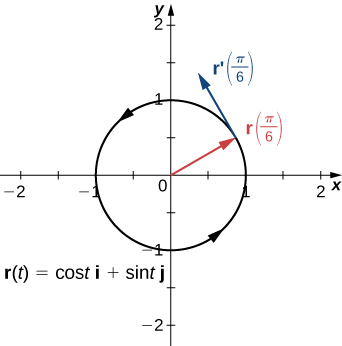
Зверніть увагу, що вектор\(\vecs{r}′\left(\dfrac{π}{6}\right)\) є дотичною до кола в точці, що відповідає\(t=\dfrac{π}{6}\). Це приклад вектора дотичної до плоської кривої, визначеної Equation\ ref {eq10}.

Визначення: дотичний вектор основної одиниці

\(C\)Дозволяти крива, визначена векторно-значною функцією\(\vecs{r}\), і припустимо, що\(\vecs{r}′(t)\) існує, коли\(\mathrm{t=t_0}\) дотичний вектор\(\vecs{r}\) в\(t=t_0\) будь-який вектор, такий, що, коли хвіст вектора розміщується в точці\(\vecs r(t_0)\) на графіку, вектор\(\vecs{r}\) дотична до кривої \(C\). Вектор\(\vecs{r}′(t_0)\) є прикладом дотичного вектора в точці\(t=t_0\). Крім того, припустимо, що\(\vecs{r}′(t)≠0\). Дотичний вектор основної одиниці\(t\) при визначено як

\[\vecs{T}(t)=\dfrac{ \vecs{r}′(t)}{‖\vecs{r}′(t)‖}, \nonumber \]

за умови\(‖\vecs{r}′(t)‖≠0\).

Вектор дотичної одиниці - це саме те, що він звучить як: одиничний вектор, який дотичний до кривої. Щоб обчислити одиничний тангенс вектора, спочатку знайдіть похідну\(\vecs{r}′(t)\). По-друге, обчислити величину похідної. Третій крок - розділити похідну на її величину.

Приклад\(\PageIndex{4}\): Finding a Unit Tangent Vector

Знайдіть одиничний тангенс вектора для кожної з наступних векторно-значних функцій:

1. \(\vecs{r}(t)=\cos t \,\mathbf{\hat{i}}+\sin t \,\mathbf{\hat{j}}\)
2. \(\vecs{u}(t)=(3t^2+2t) \,\mathbf{\hat{i}}+(2−4t^3)\,\mathbf{\hat{j}}+(6t+5)\,\mathbf{\hat{k}}\)

Рішення

1. \(\begin{array}{lrcl} \text{First step:} & \vecs r′(t) & = & − \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}} \\ \text{Second step:} & ‖\vecs r′(t)‖ & = & \sqrt{(− \sin t)^2+( \cos t)^2} = 1 \\ \text{Third step:} & \vecs T(t) & = & \dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}=\dfrac{− \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}}}{1}=− \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}} \end{array}\)
2. \(\begin{array}{lrcl} \text{First step:} & \vecs r′(t) & = & (6t+2) \,\hat{\mathbf{i}}−12t^2 \,\hat{\mathbf{j}}+6 \,\hat{\mathbf{k}} \\ \text{Second step:} & ‖\vecs r′(t)‖ & = & \sqrt{(6t+2)^2+(−12t^2)^2+6^2} \\ \text{} & \text{} & = & \sqrt{144t^4+36t^2+24t+40} \\ \text{} & \text{} & = & 2 \sqrt{36t^4+9t^2+6t+10} \\ \text{Third step:} & \vecs T(t) & = & \dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}=\dfrac{(6t+2) \,\hat{\mathbf{i}}−12t^2 \,\hat{\mathbf{j}}+6 \,\hat{\mathbf{k}}}{2 \sqrt{36t^4+9t^2+6t+10}} \\ \text{} & \text{} & = & \dfrac{3t+1}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{i}} - \dfrac{6t^2}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{j}} + \dfrac{3}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{k}} \end{array}\)

Вправа\(\PageIndex{4}\)

Знайти одиничний тангенс вектора для векторної функції

\[\vecs r(t)=(t^2−3)\,\mathbf{\hat{i}}+(2t+1) \,\mathbf{\hat{j}}+(t−2) \,\mathbf{\hat{k}}. \nonumber \]

Підказка

Виконайте ті ж дії, що і в прикладі\(\PageIndex{4}\).

Відповідь

\[\vecs T(t)=\dfrac{2t}{\sqrt{4t^2+5}}\,\mathbf{\hat{i}}+\dfrac{2}{\sqrt{4t^2+5}}\,\mathbf{\hat{j}}+\dfrac{1}{\sqrt{4t^2+5}}\,\mathbf{\hat{k}} \nonumber \]

Інтеграли векторно-значних функцій

Введено антипохідні дійсних функцій у антипохідних та визначені інтеграли дійсних функцій у визначеному інтегралі. Кожне з цих понять може бути розширено на векторно-значні функції. Крім того, так само, як ми можемо обчислити похідну векторної функції шляхом диференціації компонентних функцій окремо, ми можемо обчислити антипохідну таким же чином. Крім того, фундаментальна теорема числення застосовується і до векторних функцій.

Антипохідне векторно-значної функції з'являється в додатках. Наприклад, якщо векторно-значна функція представляє швидкість об'єкта в момент t, то її антидериватив представляє позицію. Або, якщо функція представляє прискорення об'єкта в даний момент часу, то антидериватив представляє його швидкість.

Означення: Певні та невизначені інтеграли векторно-значних функцій

Дозволяти\(f\)\(g\), і\(h\) бути інтегровні дійсні функції протягом замкнутого інтервалу\([a,b].\)

1. Невизначений інтеграл векторно-значної функції\(\vecs{r}(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}\) дорівнює

   \[\int [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}]\,dt= \left[ \int f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int g(t)\,dt \right] \,\hat{\mathbf{j}}. \nonumber \]

   Певний інтеграл векторно-значної функції дорівнює

   \[\int_a^b [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}]\,dt = \left[ \int_a^b f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int_a^b g(t)\,dt \right] \,\hat{\mathbf{j}}. \nonumber \]

2. Невизначений інтеграл векторно-значної функції\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}\) дорівнює

   \[\int [f(t) \,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} + h(t) \,\hat{\mathbf{k}}]\,dt= \left[ \int f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int g(t)\,dt \right] \,\hat{\mathbf{j}} + \left[ \int h(t)\,dt \right] \,\hat{\mathbf{k}}. \nonumber \]

   Певний інтеграл векторно-значної функції дорівнює

   \[\int_a^b [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}} + h(t) \,\hat{\mathbf{k}}]\,dt= \left[ \int_a^b f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int_a^b g(t)\,dt \right] \,\hat{\mathbf{j}} + \left[ \int_a^b h(t)\,dt \right] \,\hat{\mathbf{k}}. \nonumber \]

Оскільки невизначений інтеграл векторно-значної функції включає невизначені інтеграли компонентних функцій, кожен з цих складових інтегралів містить константу інтеграції. Всі вони можуть бути різними. Наприклад, у двовимірному випадку ми можемо мати

\[\int f(t)\,dt=F(t)+C_1 \; and \; \int g(t)\,dt=G(t)+C_2, \nonumber \]

де\(F\) і\(G\) є антипохідними\(f\) і\(g\), відповідно. Тоді

\ [\ почати {align*}\ int [f (t)\,\ hat {\ mathbf {i}} +г (t)\,\ hat {\ mathbf {j}}]\, DT &=\ лівий [\ int f (t)\, dt\ праворуч]\,\ капелюх {\ mathbf {i}} +\ лівий [\ int g (t)\, DT\ право]\,\ капелюх {\ mathbf {j}}\\ [4pt]
&= (F (t) +C_1)\,\ капелюх {\ mathbf {i}} + (G (t) +C_2)\\ капелюх {\ mathbf {j}}\\ [4pt]
&=F (t)\,\ капелюх {\\ mathbf {я}} +Г (т)\,\ капелюх {\ mathbf {j}} +C_1\,\ капелюх {\ mathbf {i}} +C_2\,\ капелюх {\ mathbf {j}}\\ [4pt]
&= F (t)\,\ капелюх {\ mathbf {i}} +Г (т)\,\ капелюх {\ mathbf {j}} +\ vecs {C}\ end {align*}\]

де\(\vecs{C}=C_1 \,\hat{\mathbf{i}}+C_2 \,\hat{\mathbf{j}}\). Тому константи інтеграції стають постійним вектором.

Приклад\(\PageIndex{5}\): Integrating Vector-Valued Functions

Обчисліть кожен з наступних інтегралів:

1. \( \displaystyle \int [(3t^2+2t) \,\hat{\mathbf{i}}+(3t−6) \,\hat{\mathbf{j}}+(6t^3+5t^2−4) \,\hat{\mathbf{k}}]\,dt\)
2. \( \displaystyle \int [⟨t,t^2,t^3⟩ \times ⟨t^3,t^2,t⟩] \,dt\)
3. \( \displaystyle \int_{0}^{\frac{\pi}{3}} [\sin 2t \,\hat{\mathbf{i}}+ \tan t \,\hat{\mathbf{j}}+e^{−2t} \,\hat{\mathbf{k}}]\,dt\)

Рішення

1. Використовується перша частина визначення інтеграла просторової кривої:
2. \ [\ почати {вирівнювати*}\ int [(3t^2+2t)\,\ капелюх {\ mathbf {i}} + (3t−6)\,\ капелюх {\ mathbf {j}} + (6t^3+5t^2−4)\,\ капелюх {\ mathbf {k}}]\, dt =\ лівий [\ int 3−4) t^2+2t\, dt\ право]\,\ hat {\ mathbf {i}} +\ лівий [\ int 3t−6\, dt\ праворуч]\,\ капелюх {\ mathbf {j}} +\ ліворуч [\ int 6t^3+5t^2−4\, dt\ праворуч]\,\ капелюх {\ mathbf {k}}\ [4pt]
   & = (т ^ 3+т ^ 2) \,\ капелюх {\ mathbf {i}} +\ ліворуч (\ frac {3} {2} t^2−6t\ праворуч)\,\ капелюх {\ mathbf {j}} +\ ліворуч (\ frac {3} {2} t^4+\ frac {5} {3} t^3−4t\ праворуч)\,\ капелюх {\ math-bt\ праворуч)\ f {k}} +\ векс С.\ end {align*}\]
3. Спочатку розрахуйте\(⟨t,t^2,t^3⟩ \times ⟨t^3,t^2,t⟩:\)

   \ [\ почати {вирівнювати*} ⟨t, t^2, t^3⟩\ раз ⟨t^3, t^2, t⟩ &=\ почати {vmatrix}\ капелюх {\ mathbf {i}} &\,\ капелюх {\ mathbf {k}}\\ t & t^3\ t^3 & t^2 & t\ end {vmatrix}\\ [4pt]
   &= (t^2 (t) −t^3 (t^2))\,\ hat {\ mathbf {i}} − (t^2−t^3 (t^3))\,\ капелюх {\ mathbf {j}} + (t (t^2) −t ^2 (t^3))\,\ капелюх {\ mathbf {k}}\\ [4pt]
   & =( t^3−t^5)\,\ капелюх {\ mathbf {i}} + (t^6−t^2)\,\ капелюх {\ mathbf {j}} + (t^3−t^5)\,\ капелюх {\ mathbf {j}} + (t^3−t^5)\,\ капелюх {\ mathbf {j}} thbf {k}}. \ end {вирівнювати*}\ nonumber\]

   Далі, підставити це назад в інтеграл і інтегрувати:

   \ [\ почати {вирівнювати*}\ int [⟨t, t^2, t^3⟩\ раз ⟨t^3, t^2, t⟩]\, DT &=\ int (t^3−t^5)\,\ капелюх {\ mathbf {i}} + (t^6−t^2)\,\ капелюх {\ mathbf {j}} + (t^6−t^2)\,\ капелюх {\ mathbf {j}} + (t^6−t^2)\ 3−t^5)\,\ hat {\ mathbf {k}}\, dt\\ [4pt]
   &=\ лівий (\ frac {t^4} {4}} −\ frac {t^6} {7}\ праворуч)\,\ капелюх {\ mathbf {i}} +\ ліворуч (\ frac {t^7} {7}} −\ frac t^3} {3}\ право)\,\ hat {\ mathbf {j}} +\ ліворуч (\ frac {t^4} {4} −\ frac {t^6} {6}\ праворуч)\,\ hat {\ mathbf {k}} +\ vecs C\ end {align*}\]

4. Скористайтеся другою частиною визначення інтеграла просторової кривої:

   \ [\ почати {align*}\ int_0^ {\ frac {\ pi} {\ pi} {3}} [\ sin 2t\,\ капелюх {\ mathbf {i}} +\ тан т\,\ капелюх {\ mathbf {j}} +e^ {−2t}\,\ капелюх {\ mathbf {k}}]\, DT &=\ лівий [int_0^ {\ frac {π} {3}}\ sin 2t\, dt\ праворуч]\,\ hat {\ mathbf {i}} +\ лівий [\ int_0^ {\ frac {π} {3}}\ тан t\, dt\ праворуч]\,\ капелюх {\ mathbf {j}} +\ лівий [\ int_0^ {fra c {π} {3}} e^ {−2t}\, dt\ право] \,\ капелюх {\ mathbf {k}}\\ [4pt]
   &= (-\ tfrac {1} {2}\ cos 2t)\ Великий\ vert_ {0} ^ {π/3}\,\ капелюх {\ mathbf {i}} − (\ ln |\ cos t|)\ Великий\ vert_ {0} ^ {π/3}\,\ капелюх {\ mathbf {j}} −\ лівий (\ tfrac {1} {2} e^ {−2t}\ праворуч)\ Великий\ vert_ {0} ^ {π/3}\,\ капелюх {\ mathbf {k}}\\ [4pt]
   &=\ лівий (−\ tfrac {1} {2}\ cos\ tfrac {2π} {3} +\ tfrac {1} {2}\ cos 0\ праворуч)\,\ hat {\ mathbf {i}} −\ ліворуч (\ ln\ ліворуч (\ cos\ tfrac {π} {3}\ праворуч) −\ ln (\ cos 0)\ праворуч)\,\ капелюх {\ mathbf {j}}} −\ ліворуч (\ tfrac {1} {2} ^ e^ {−2π/3} −\ tfrac {1} {2} e^ {−2 (0)}\ право)\,\ капелюх {\ mathbf {k}}\\ [4pt]
   & =\ ліворуч (\ tfrac {1} {4} +\ tfrac {1} {2}\ праворуч)\,\ hat {\ mathbf {i} − (−\ ln 2)\,\ hat {\ mathbf {j}} −\ ліворуч (\ tfrac {1} {2} e^ {−2π/3}} −\ tfrac {1} {2}\ праворуч)\,\ hat {\ mathbf {k}}\\ [4pt]
   &=\ tfrac {3} {4}\,\ капелюх {\ mathbf {i}} +\ ln 2)\,\ hat {\ mathbf {j}} +\ лівий (\ tfrac {1} {2} −\ trac {1} {2} e^ {−2π/3}\ праворуч)\,\ hat {\ mathbf {k}}. \ end {вирівнювати*}\]

Вправа\(\PageIndex{5}\)

Обчисліть наступний інтеграл:

\[\int_1^3 [(2t+4) \,\mathbf{\hat{i}}+(3t^2−4t) \,\mathbf{\hat{j}}]\,dt \nonumber \]

Підказка

Використовуйте визначення певного інтеграла плоської кривої.

Відповідь

\[\int_1^3 [(2t+4) \,\mathbf{\hat{i}}+(3t^2−4t) \,\mathbf{\hat{j}}]\,dt = 16 \,\mathbf{\hat{i}}+10 \,\mathbf{\hat{j}} \nonumber \]

Резюме

• Щоб обчислити похідну векторно-значної функції, обчислити похідні компонентних функцій, потім повернути їх у нову векторно-значну функцію.
• Багато властивостей диференціації скалярних функцій також відносяться до векторно-значних функцій.
• Похідна векторно-значної функції також\(\vecs r(t)\) є дотичним вектором до кривої. Одиничний\(\vecs T(t)\) тангенсний вектор обчислюється діленням похідної векторно-значної функції на її величину.
• Антипохідне векторно-значної функції знайдено шляхом знаходження антипохідних компонентних функцій, а потім їх зближення у векторно-значну функцію.
• Визначений інтеграл векторно-значної функції знаходять шляхом знаходження певних інтегралів компонентних функцій, а потім їх зближення у векторно-значну функцію.

Ключові рівняння

• Похідна векторно-значної функції\[\vecs r′(t) = \lim \limits_{\Delta t \to 0} \dfrac{\vecs r(t+\Delta t)−\vecs r(t)}{ \Delta t} \nonumber \]
• Дотичний вектор основної одиниці\[\vecs T(t)=\frac{\vecs r′(t)}{‖\vecs r′(t)‖} \nonumber \]
• Невизначений інтеграл векторно-значної функції\[\int [f(t) \,\mathbf{\hat{i}}+g(t)\,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}]\,dt= \left[ \int f(t)\,dt \right] \,\mathbf{\hat{i}}+ \left[ \int g(t)\,dt \right] \,\mathbf{\hat{j}} + \left[ \int h(t)\,dt \right] \,\mathbf{\hat{k}}\nonumber \]
• Певний інтеграл векторно-значної функції\[\int_a^b [f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}]\,dt= \left[\int_a^b f(t)\,dt \right] \,\mathbf{\hat{i}}+ \left[ \int _a^b g(t)\,dt \right] \,\mathbf{\hat{j}} + \left[ \int _a^b h(t)\,dt \right] \,\mathbf{\hat{k}}\nonumber \]

Глосарій

певний інтеграл векторно-значної функції

вектор, отриманий шляхом обчислення певного інтеграла кожної з складових функцій заданої векторно-значної функції, з подальшим використанням результатів як складових результуючої функції

похідна векторно-значної функції

похідна векторно-значної функції\(\vecs{r}(t)\) дорівнює\(\vecs{r}′(t) = \lim \limits_{\Delta t \to 0} \frac{\vecs r(t+\Delta t)−\vecs r(t)}{ \Delta t}\), якщо межа існує

невизначений інтеграл векторно-значної функції

векторно-значна функція з похідною, яка дорівнює заданій векторної функції

дотичний вектор основної одиниці

тангенс одиничного вектора до кривої C

тангенс вектор

\(\vecs{r}(t)\)на\(t=t_0\) будь-якому векторі\(\vecs v\) таким чином, що, коли хвіст вектора розміщений в точці\(\vecs r(t_0)\) на графіку, вектор\(\vecs{v}\) дотичний до кривої C