6.7: Інтеграли, експоненціальні функції та логарифми

Цілі навчання

• Запишіть визначення натурального логарифма як інтеграла.
• Розпізнати похідну натурального логарифма.
• Інтегруйте функції, що включають природну логарифмічну функцію.
• Визначте число$e$ через інтеграл.
• Розпізнати похідну і інтеграл експоненціальної функції.
• Довести властивості логарифмів і експоненціальних функцій за допомогою інтегралів.
• Висловіть загальні логарифмічні та експоненціальні функції через натуральні логарифми та експоненціальні.

Ми вже розглядали експоненціальні функції та логарифми в попередніх розділах. Однак ми розглянули деякі ключові деталі в попередніх обговореннях. Наприклад, ми не вивчали, як лікувати експоненціальні функції з експонентами, які є ірраціональними. Визначення числа е - ще одна область, де попередня розробка була дещо неповною. Тепер у нас є інструменти для вирішення цих понять більш математично суворо, і ми робимо це в цьому розділі.

Для цілей цього розділу припустимо, що ми ще не визначили натуральний логарифм$e$, число або будь-яку з формул інтеграції та диференціації, пов'язаних з цими функціями. До кінця розділу ми вивчимо ці поняття математично суворо (і побачимо, що вони узгоджуються з поняттями, які ми дізналися раніше). Розріз починаємо з визначення натурального логарифма через інтеграл. Це визначення і формує основу для перетину. З цього визначення ми виведемо формули диференціації, визначаємо число$e$ і розширюємо ці поняття до логарифмів і експоненціальних функцій будь-якої бази.

Натуральний логарифм як інтеграл

Нагадаємо правило потужності для інтегралів:

$$∫ x^n \,dx = \dfrac{x^{n+1}}{n+1} + C , \quad n≠−1. \nonumber$$

Зрозуміло, що це не працює, коли$n=−1,$ як це змусило б нас розділити на нуль. Отже, з чим ми робимо$\displaystyle ∫\dfrac{1}{x}\,dx$? Нагадаємо з фундаментальної теореми числення, яка$\displaystyle ∫^x_1\dfrac{1}{t}dt$ є антипохідною$\dfrac{1}{x}.$ Тому ми можемо зробити наступне визначення.

Визначення: Натуральний логарифм

For$x>0$, Визначте натуральну функцію логарифму за

$$\ln x=∫^x_1\dfrac{1}{t}\,dt. \nonumber$$

Бо$x>1$, це просто площа під кривою$y=\dfrac{1}{t}$ від$1$ до$x$. Бо$x<1$, у нас є

$$∫^x_1\dfrac{1}{t}\,dt=−∫^1_x\dfrac{1}{t}\,dt, \nonumber$$

тому в даному випадку це негатив області під кривою від$x$ до$1$ (див. Наступний малюнок).

Малюнок$\PageIndex{1}$: (а) Коли$x>1$ натуральний логарифм - це площа під кривою$y=1/t$ від$1$ до$x$. (b) Коли$x<1$ натуральний логарифм є негативним площі під кривою від$x$ до$1$.

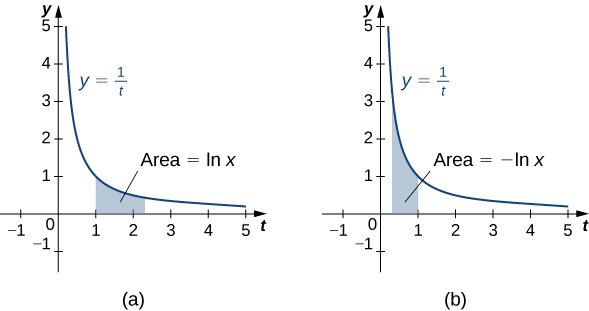
Зауважте, що$\ln 1=0$. Крім того, функція$y=\dfrac{1}{t}>0$ для$x>0$. Тому за властивостями інтегралів зрозуміло, що$\ln x$ збільшується для$x>0$.

Властивості натурального логарифма

Через те, як ми визначили натуральний логарифм, наступна формула диференціації випадає відразу в результаті фундаментальної теореми числення.

Визначення: Похідна натурального логарифма

For$x>0$, похідна натурального логарифма задається

$$\dfrac{d}{dx}\Big( \ln x \Big) = \dfrac{1}{x}. \nonumber$$

Наслідок похідної натурального логарифма

$\ln x$Функція диференційовна; отже, вона безперервна.

Графік$\ln x$ показаний на рис. Зверніть увагу, що він безперервний протягом усієї області$(0,∞)$.

Малюнок$\PageIndex{2}$: Графік$f(x)=\ln x$ показує, що це неперервна функція.

Приклад$\PageIndex{1}$: Calculating Derivatives of Natural Logarithms

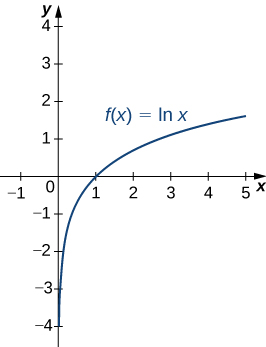
Обчисліть такі похідні:

1. $\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)$
2. $\dfrac{d}{dx}\Big((\ln (3x))^2\Big)$

Рішення

Нам потрібно застосувати правило ланцюга в обох випадках.

1. $\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)=\dfrac{15x^2}{5x^3−2}$
2. $\dfrac{d}{dx}\Big((\ln (3x))^2\Big)=\dfrac{2(\ln (3x))⋅3}{3x}=\dfrac{2(\ln (3x))}{x}$

Вправа$\PageIndex{1}$

Обчисліть такі похідні:

1. $\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)$
2. $\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)$

Підказка

Застосуйте щойно надану формулу диференціації та використовуйте правило ланцюга в міру необхідності.

Відповідь

а.$\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)=\dfrac{4x+1}{2x^2+x}$

б.$\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)=\dfrac{6\ln (x^3)}{x}$

Зауважте, що якщо ми використовуємо функцію абсолютного значення і створимо нову функцію$\ln |x|$, ми можемо розширити область натурального логарифма для включення$x<0$. Потім$\dfrac{d}{dx}\Big( \ln x \Big)=\dfrac{1}{x}$. Це породжує звичну формулу інтеграції.

Інтеграл$\frac{1}{u} \, du$

Натуральний логарифм є антипохідним функції$f(u)=\dfrac{1}{u}$:

$$∫\dfrac{1}{u}\,du=\ln |u|+C. \nonumber$$

Приклад$\PageIndex{2}$: Calculating Integrals Involving Natural Logarithms

Обчисліть інтеграл$\displaystyle ∫\dfrac{x}{x^2+4}\,dx.$

Рішення

Використовуючи$u$ -підстановку, нехай$u=x^2+4$. Тоді$du=2x\,dx$ і у нас

$\displaystyle ∫\dfrac{x}{x^2+4}\,dx=\dfrac{1}{2}∫\dfrac{1}{u}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln |x^2+4|+C=\dfrac{1}{2}\ln (x^2+4)+C.$

Вправа$\PageIndex{2}$

Обчисліть інтеграл$\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx.$

Підказка

Застосуйте формулу інтеграції, надану раніше, та використовуйте U-підстановку у міру необхідності.

Відповідь

$\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx=\dfrac{1}{3}\ln ∣x^3+6∣+C$

Хоча ми назвали нашу функцію «логарифмом», ми насправді не довели, що будь-яка з властивостей логарифмів має для цієї функції. Ми робимо це тут.

Властивості натурального логарифма

Якщо$a,\, b>0$ і$r$ є раціональним числом, то

1. $\ln 1=0$
2. $\ln (ab)=\ln a+\ln b$
3. $\ln \left(\dfrac{a}{b}\right)=\ln a−\ln b$
4. $\ln \left(a^r\right)=r\ln a$

Доказ

i. за визначенням$\displaystyle \ln 1=∫^1_1\dfrac{1}{t}\,dt=0.$

II. У нас є

$\displaystyle \ln (ab)=∫^{ab}_1\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt.$

Використовуйте$u-substitution$ на останньому інтегралі в цьому виразі. Нехай$u=t/a$. Тоді$du=(1/a)dt.$ Крім того$t=a,\, u=1$, коли і коли$t=ab,\, u=b.$ Так ми отримуємо

$\displaystyle \ln (ab)=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_1\dfrac{a}{t}⋅\dfrac{1}{a}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^b_1\dfrac{1}{u}\,du=\ln a+\ln b.$

iii. Зверніть увагу, що

$\dfrac{d}{dx}\Big(\ln (x^r)\Big)=\dfrac{rx^{r−1}}{x^r}=\dfrac{r}{x}$.

Крім того,

$\dfrac{d}{dx}\Big((r\ln x)\Big)=\dfrac{r}{x}.$

Оскільки похідні цих двох функцій однакові, за фундаментальною теоремою числення вони повинні відрізнятися константою. Отже, у нас є

$\ln (x^r)=r\ln x+C$

для деяких постійних$C$. Беручи$x=1$, отримуємо

$\ln (1^r)=r\ln (1)+C$

$0=r(0)+C$

$C=0.$

Таким чином$\ln (x^r)=r\ln x$ і доказ завершений. Зауважте, що ми можемо розширити цю властивість до ірраціональних значень$r$ пізніше в цьому розділі.

Частина III. випливає з частин ii. і iv. і доказ залишається вам.

□

Приклад$\PageIndex{3}$: Using Properties of Logarithms

Використовуйте властивості логарифмів, щоб спростити наступний вираз в один логарифм:

$\ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right).$

Рішення

У нас є

$\ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right)=\ln (3^2)−2 \ln 3+\ln (3^{−1})=2\ln 3−2\ln 3−\ln 3=−\ln 3.$

Вправа$\PageIndex{3}$

Використовуйте властивості логарифмів, щоб спростити наступний вираз в один логарифм:

$\ln 8−\ln 2−\ln \left(\tfrac{1}{4}\right)$

Підказка

Застосовуємо властивості логарифмів.

Відповідь

$4\ln 2$

Визначення числа e

Тепер, коли у нас є натуральний логарифм визначено, ми можемо використовувати цю функцію для визначення числа$e$.

Визначення:$e$

Число$e$ визначається як дійсне число, таке, що

$$\ln e=1\nonumber$$

Якщо говорити по-іншому, площа під кривою$y=1/t$ між$t=1$ і$t=e$ є$1$ (рис.). Доказ того, що таке число існує і є унікальним, залишається вам. (Підказка: Використовуйте теорему проміжних значень, щоб довести існування і той факт,$\ln x$ що збільшується, щоб довести унікальність.)

Малюнок:$\PageIndex{3}$ Площа під кривою від до$1$$e$ дорівнює одиниці.

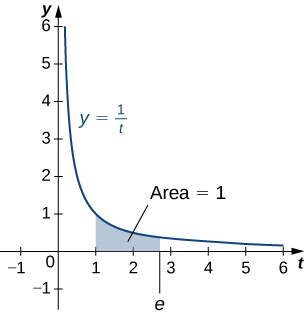
Число$e$ може бути показано як ірраціональне, хоча ми не будемо робити цього тут (див Студентський проект у серії Тейлора та Маклоріна). Його приблизне значення задається

$e≈2.71828182846.$

Експоненціальна функція

Тепер звернемо увагу на функцію$e^x$. Зверніть увагу, що натуральний логарифм один до одного і тому має обернену функцію. Поки що ми позначимо цю зворотну функцію шляхом$\exp x$. Потім,

$$\exp(\ln x)=x \nonumber$$

для$x>0$ і

$$\ln (\exp x)=x \nonumber$$

для всіх$x$.

На наступному малюнку показані графіки$\exp x$ і$\ln x$.

Малюнок$\PageIndex{4}$: Графіки$\ln x$ і$\exp x$.

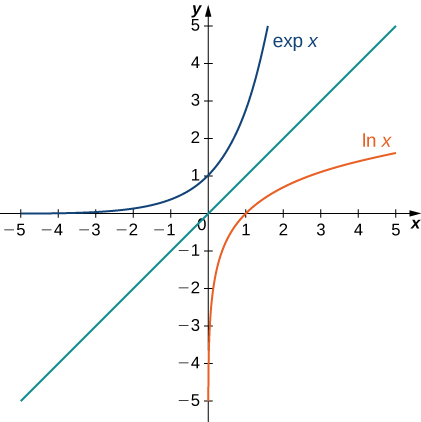
Ми висуваємо це гіпотезу$\exp x=e^x$. Для раціональних значень$x$, це легко показати. Якщо$x$ раціонально, то маємо$\ln (e^x)=x\ln e=x$. Таким чином, коли$x$ раціонально,$e^x=\exp x$. Для ірраціональних значень$x$, ми просто визначаємо$e^x$ як обернену функцію$\ln x$.

Визначення

Для будь-якого дійсного числа$x$$y=e^x$ визначте число, для якого

$$\ln y=\ln (e^x)=x. \nonumber$$

Тоді у нас є$e^x=\exp x$ для всіх$x$, і таким чином

$e^{\ln x}=x$для$x>0$ і$\ln (e^x)=x$

для всіх$x$.

Властивості експоненціальної функції

Оскільки експоненціальна функція була визначена з точки зору оберненої функції, а не з точки зору сили,$e$ ми повинні перевірити, чи дотримуються звичайні закони експонентів для функції$e^x$.

Властивості експоненціальної функції

Якщо$p$ і$q$ є будь-якими дійсними числами і$r$ є раціональним числом, то

1. $e^pe^q=e^{p+q}$
2. $\dfrac{e^p}{e^q}=e^{p−q}$
3. $(e^p)^r=e^{pr}$

Доказ

Зверніть увагу, що якщо$p$ і$q$ є раціональними, властивості тримаються. Однак, якщо$p$ або$q$ є ірраціональними, ми повинні застосувати зворотне визначення функції$e^x$ та перевірити властивості. Тут перевіряється тільки перша властивість, інші два залишаються вам. У нас є

$$\ln (e^pe^q)=\ln (e^p)+\ln (eq)=p+q=\ln (e^{p+q}).\nonumber$$

Так як$\ln x$ один до одного, то

$$e^pe^q=e^{p+q}.\nonumber$$

□

Як і частина iv. властивостей логарифма, ми можемо розширити властивість iiii. до ірраціональних значень$r$, і ми робимо це до кінця розділу.

Ми також хочемо перевірити формулу диференціації для функції$y=e^x$. Для цього нам потрібно використовувати неявну диференціацію. Нехай$y=e^x$. Тоді

$$\begin{align*} \ln y &=x \\[5pt] \dfrac{d}{dx}\Big(\ln y\Big) &=\dfrac{d}{dx}\Big(x\Big) \\[5pt] \dfrac{1}{y}\dfrac{dy}{dx} &=1 \\[5pt] \dfrac{dy}{dx} &=y. \end{align*}$$

Таким чином, ми бачимо

$$\dfrac{d}{dx}\Big(e^x\Big)=e^x \nonumber$$

за бажанням, що призводить відразу до формули інтеграції

$$∫e^x \,dx=e^x+C. \nonumber$$

Ми застосовуємо ці формули в наступних прикладах.

Приклад$\PageIndex{4}$: Using Properties of Exponential Functions

Оцініть наступні похідні:

1. $\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)$
2. $\dfrac{d}{dx}\Big(e^{3x^2}\Big)$

Рішення

Застосовуємо правило ланцюга в міру необхідності.

1. $\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)=\dfrac{d}{dt}\Big(e^{3t+t^2}\Big)=e^{3t+t^2}(3+2t)$
2. $\dfrac{d}{dx}\Big(e^{3x^2}\Big)=e^{3x^2}6x$

Вправа$\PageIndex{4}$

Оцініть наступні похідні:

1. $\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)$
2. $\dfrac{d}{dt}\Big((e^{2t})^3\Big)$

Підказка

Використовуйте властивості експоненціальних функцій і правило ланцюга в міру необхідності.

Відповідь

а.$\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)=e^{x^{2−5x}}(2x−5)$

б.$\dfrac{d}{dt}\Big((e^{2t})^3\Big)=6e^{6t}$

Приклад$\PageIndex{5}$: Using Properties of Exponential Functions

Оцініть наступний інтеграл:$\displaystyle ∫2xe^{−x^2}\,dx.$

Рішення

Використовуючи$u$ -підстановку, нехай$u=−x^2$. Тоді$du=−2x\,dx,$ і у нас

$\displaystyle ∫2xe^{−x^2}\,dx=−∫e^u\,du=−e^u+C=−e^{−x^2}+C.$

Вправа$\PageIndex{5}$

Оцініть наступний інтеграл:$\displaystyle ∫\dfrac{4}{e^{3x}}\,dx.$

Підказка

Використовувати властивості експоненціальних функцій і в$u-substitution$ міру необхідності.

Відповідь

$\displaystyle ∫\dfrac{4}{e^{3x}}\,dx=−\dfrac{4}{3}e^{−3x}+C$

Загальні логарифмічні та експоненціальні функції

Ми закриваємо цей розділ, дивлячись на експоненціальні функції та логарифми з основами, відмінними від$e$. Експоненціальні функції - це функції виду$f(x)=a^x$. Зауважте$a=e$, що якщо, ми все ще не маємо математично суворого визначення цих функцій для ірраціональних показників. Давайте виправимо це тут, визначаючи функцію з$f(x)=a^x$ точки зору експоненціальної функції$e^x$. Потім ми досліджуємо логарифми з основами, відмінними від e, як обернені функції експоненціальних функцій.

Визначення: Експоненціальна функція

Для будь-якого$a>0,$ і для будь-якого дійсного числа$x$ визначте$y=a^x$ наступним чином:

$$y=a^x=e^{x \ln a}. \nonumber$$

Тепер$a^x$ визначається строго для всіх значень$x$. Це визначення також дозволяє узагальнити властивість iv. логарифмів і властивості iii. експоненціальних функцій застосовувати як до раціональних, так і до ірраціональних значень$r$. Це просто показати, що властивості експонентів мають для загальних експоненціальних функцій, визначених таким чином.

Давайте тепер застосуємо це визначення, щоб обчислити формулу диференціації для$a^x$. У нас є

$\dfrac{d}{dx}\Big(a^x\Big)=\dfrac{d}{dx}\Big(e^{x\ln a}\Big)=e^{x\ln a}\ln a=a^x\ln a.$

Відповідна формула інтеграції слід негайно.

Похідні та інтеграли із загальними експоненціальними функціями

Нехай$a>0.$ тоді,

$$\dfrac{d}{dx}\Big(a^x\Big)=a^x \ln a \nonumber$$

і

$$∫a^x\,dx=\dfrac{1}{\ln a}a^x+C. \nonumber$$

Якщо$a≠1$,$a^x$ то функція один-на-один і має чітко визначену зворотну. Його зворотна позначається символом$\log_a x$. Потім,

$y=\log_a x$якщо і тільки якщо$x=a^y.$

Зверніть увагу, що загальні функції логарифма можуть бути записані через натуральний логарифм. Нехай$y=\log_a x.$ тоді,$x=a^y$. Взявши натуральний логарифм обох сторін цього другого рівняння, отримаємо

\ [\ почати {вирівнювати*}\ ln x &=\ ln (a^y)\\\ [5pt]
\ ln x &=y\ n a\\ [5pt]
y&=\ dfrac {\ ln x} {\ ln a}\\ [5pt]\ log_a x&=
\ dfrac {\ ln x} {\ ln a} {\ ln a}. \ end {вирівнювати*}\]

Таким чином, ми бачимо, що всі логарифмічні функції є постійними кратними одна одній. Далі ми використовуємо цю формулу, щоб знайти формулу диференціації логарифма з основою$a$. Знову нехай$y=\log_a x$. Потім,

\ [\ почати {вирівнювати*}\ dfrac {dh} {dx} &=\ dfrac {d} {dx}\ Великий (\ log_a x\ Великий)\\ [5pt]
&=\ dfrac {d} {dx}\ ліворуч (\ dfrac {\ ln x} {\ на а}\ праворуч)\\ [5pt]
& =(\ dfrac {1} {\ ln a})\ dfrac {d} {dx}\ Великий (\ ln x\ Великий)\\ [5pt]
&=\ dfrac {1} {\ ln a} ⋅\ dfrac {1} =\ dfrac {1} {x\ ln a}\ кінець {align*}\]

Похідні функцій загального логарифму

Нехай$a>0.$ тоді,

$$\dfrac{d}{dx}\Big(\log_a x\Big)=\dfrac{1}{x\ln a}. \nonumber$$

Приклад$\PageIndex{6}$: Calculating Derivatives of General Exponential and Logarithm Functions

Оцініть наступні похідні:

1. $\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)$
2. $\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)$

Рішення: Нам потрібно застосувати правило ланцюга в міру необхідності.

1. $\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t}⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t+t^2}\Big)=2^{2t+t^2}\ln (2)(2+2t)$
2. $\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)=\dfrac{1}{(7x^2+4)(\ln 8)}(14x)$

Вправа$\PageIndex{6}$

Оцініть наступні похідні:

1. $\dfrac{d}{dt}\Big(4^{t^4}\Big)$
2. $\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)$

Підказка

Використовуйте формули і застосовуйте правило ланцюга в міру необхідності.

Відповідь

а.$\dfrac{d}{dt}\Big(4^{t^4}\Big)=4^{t^4}(\ln 4)(4t^3)$

б.$\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)=\dfrac{x}{(\ln 3)(x^2+1)}$

Приклад$\PageIndex{7}$: Integrating General Exponential Functions

Оцініть наступний інтеграл:$\displaystyle ∫\dfrac{3}{2^{3x}}\,dx.$

Рішення

Використовуйте$u-substitution$ і нехай$u=−3x$. Тоді$du=−3\,dx$ і у нас

$$∫\dfrac{3}{2^{3x}}\,dx=∫3⋅2^{−3x}\,dx=−∫2^u\,du=−\dfrac{1}{\ln 2}2^u+C=−\dfrac{1}{\ln 2}2^{−3x}+C.\nonumber$$

Вправа$\PageIndex{7}$

Оцініть наступний інтеграл:$\displaystyle ∫x^2 2^{x^3}\,dx.$

Підказка

Використання властивостей експоненціальних функцій та u-підстановки

Відповідь

$\displaystyle ∫x^2 2^{x^3}\,dx=\dfrac{1}{3\ln 2}2^{x^3}+C$

Ключові концепції

• Раніше обробка логарифмів і експоненціальних функцій не визначала функції точно і формально. Цей розділ розробляє поняття математично суворо.
• Наріжним каменем розвитку є визначення натурального логарифма через інтеграл.
• Потім функція$e^x$ визначається як обернена натуральним логарифмом. Загальні експоненціальні функції визначаються$e^x$ термінами, а відповідні обернені функції є загальними логарифмами.
• Знайомі властивості логарифмів і експонентів все ще тримаються в цьому більш суворому контексті.

Ключові рівняння

• Функція натурального логарифма
• $\displaystyle \ln x=∫^x_1\dfrac{1}{t}\,dt$
• Експоненціальна функція$y=e^x$
• $\ln y=\ln (e^x)=x$