3.2: Похідна як функція
- Page ID
- 62290
- Визначте похідну функцію заданої функції.
- Графік — похідна функція з графа заданої функції.
- Створити зв'язок між похідними і безперервністю.
- Опишіть три умови, коли функція не має похідної.
- Поясніть значення похідної вищого порядку.
Як ми бачили, похідна функції в даній точці дає нам швидкість зміни або нахилу дотичної лінії до функції в цій точці. Якщо ми диференціюємо позиційну функцію в даний час, ми отримаємо швидкість в той час. Здається розумним зробити висновок, що знання похідної функції в кожній точці дасть цінну інформацію про поведінку функції. Однак процес знаходження похідної навіть у декількох значень за допомогою методів попереднього розділу швидко став би досить нудним. У цьому розділі ми визначаємо похідну функцію і вивчимо процес її знаходження.
Похідні функції
Похідна функція дає похідну функції в кожній точці області початкової функції, для якої визначено похідну. Ми можемо формально визначити похідну функцію наступним чином.
\(f\)Дозволяти бути функцією. Похідна функція, позначається\(f'\), - це функція, область якої складається з тих значень\(x\) таких, що існує наступна межа:
\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(x)}{h}. \label{derdef} \]
\(f(x)\)Функція, як кажуть, диференційована\(a\) при\(f'(a)\) наявності. Більш загально, функція вважається диференційованою,\(S\) якщо вона диференційована в кожній точці відкритої множини\(S\), а диференційована функція - це та, в якій\(f'(x)\) існує на її області.
У наступних прикладах ми використовуємо Equation\ ref {derdef} для пошуку похідної функції.
Знайдіть похідну від\(f(x)=\sqrt{x}\).
Рішення
Почніть безпосередньо з визначення похідної функції.
\(f(x)=\sqrt{x}\)Підставляємо\(f(x+h)=\sqrt{x+h}\) і в\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\).
| \(f'(x)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}\) | Помножте чисельник і знаменник на,\(\sqrt{x+h}+\sqrt{x}\) не розподіляючи в знаменнику. |
| \(=\displaystyle\lim_{h→0}\frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Множимо чисельники і спрощуємо. |
| \(=\displaystyle\lim_{h→0}\frac{1}{\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Скасувати\(h\). |
| \(=\dfrac{1}{2\sqrt{x}}\) | Оцініть ліміт |
Знайдіть похідну функції\(f(x)=x^2−2x\).
Рішення
Виконайте ту ж процедуру тут, але без необхідності множення на сполучений.
\(f(x+h)=(x+h)^2−2(x+h)\)\(f(x)=x^2−2x\)Замінюємо і в\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle\lim_{h→0}\frac{((x+h)^2−2(x+h))−(x^2−2x)}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{x^2+2xh+h^2−2x−2h−x^2+2x}{h}\) | Розгорнути\((x+h)^2−2(x+h)\). |
| \(=\displaystyle\lim_{h→0}\frac{2xh−2h+h^2}{h}\) | Спростити |
| \(=\displaystyle\lim_{h→0}\frac{h(2x−2+h)}{h}\) | Фактор\(h\) з чисельника |
| \(=\displaystyle\lim_{h→0}(2x−2+h)\) | Скасувати загальний фактор\(h\) |
| \(=2x−2\) | Оцініть ліміт |
Знайдіть похідну від\(f(x)=x^2\).
- Підказка
-
Використовуйте Equation\ ref {derdef} і дотримуйтесь прикладу.
- Відповідь
-
\(f'(x)=2x\)
Ми використовуємо безліч різних позначень для вираження похідної функції. У прикладі\(\PageIndex{2}\) ми показали, що якщо\(f(x)=x^2−2x\), то\(f'(x)=2x−2\). Якби ми висловили цю функцію у вигляді\(y=x^2−2x\), ми могли б висловити похідну як\(y′=2x−2\) або\(\dfrac{dy}{dx}=2x−2\). Ми могли б передати ту ж інформацію, написавши\(\dfrac{d}{dx}\left(x^2−2x\right)=2x−2\). Таким чином, для функції\(y=f(x)\) кожне з наступних позначень являє собою похідну від\(f(x)\):
\(f'(x), \quad \dfrac{dy}{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\).
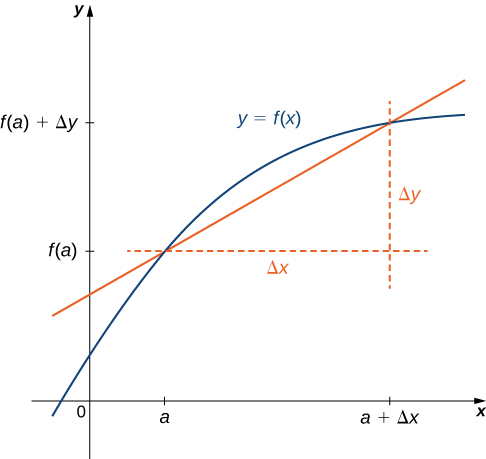
На місці\(f'(a)\) ми також можемо використовувати\(\dfrac{dy}{dx}\Big|_{x=a}\). Використання\(\dfrac{dy}{dx}\) позначень (званих позначенням Лейбніца) досить поширене в техніці та фізиці. Щоб краще зрозуміти це позначення, нагадайте, що похідна функції в точці є межею нахилів січних ліній, коли січні лінії наближаються до дотичної лінії. Нахили цих січних ліній часто виражаються в тому вигляді,\(\dfrac{Δy}{Δx}\) де\(Δy\) знаходиться різниця\(y\) значень, відповідних різниці\(x\) значень, які виражаються як\(Δx\) (рис.\(\PageIndex{1}\)). Таким чином, похідна, яку можна розглядати як миттєву швидкість зміни\(y\) щодо\(x\), виражається як
\(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\).
Графік похідної
Ми вже обговорювали, як графікувати функцію, тому, враховуючи рівняння функції або рівняння похідної функції, ми могли б її графікувати. Враховуючи обидва, ми очікуємо побачити відповідність між графіками цих двох функцій, оскільки\(f'(x)\) дає швидкість зміни функції\(f(x)\) (або нахил дотичної лінії до\(f(x)\)).
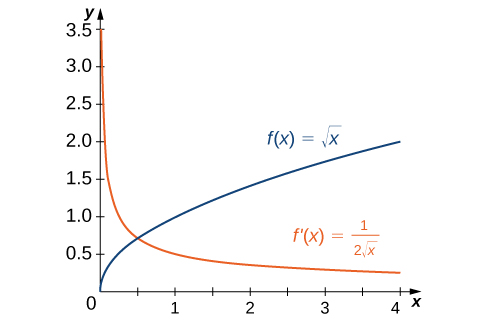
У прикладі\(\PageIndex{1}\), ми виявили, що для\(f(x)=\sqrt{x}\),\(f'(x)=\frac{1}{2\sqrt{x}}\). Якщо ми графуємо ці функції на однакових осях, як на малюнку\(\PageIndex{2}\), ми можемо використовувати графіки, щоб зрозуміти взаємозв'язок між цими двома функціями. По-перше, ми помічаємо,\(f(x)\) що збільшується по всій його області, а це означає, що нахили його дотичних ліній у всіх точках позитивні. Отже, ми очікуємо\(f'(x)>0\) для всіх значень x у своїй області. Крім того,\(x\) зі збільшенням нахили дотичних ліній до\(f(x)\) зменшуються, і ми очікуємо відповідного зменшення\(f'(x)\). Ми також спостерігаємо,\(f(0)\) що не визначено і що\(\displaystyle \lim_{x→0^+}f'(x)=+∞\), що відповідає вертикальній дотичній до\(f(x)\) at\(0\).
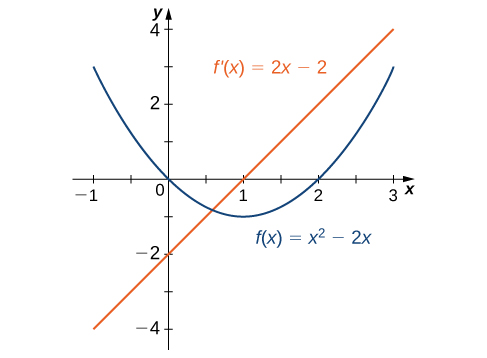
У\(\PageIndex{2}\) прикладі ми виявили, що для\(f(x)=x^2−2x,\; f'(x)=2x−2\). Графіки цих функцій наведені на рис\(\PageIndex{3}\). Спостерігайте,\(f(x)\) що зменшується для\(x<1\). Для цих же значень\(x\),\(f'(x)<0\). Для значень\(x>1\),\(f(x)\) є збільшенням і\(f'(x)>0\). Також,\(f(x)\) має горизонтальну дотичну при\(x=1\) і\(f'(1)=0\).
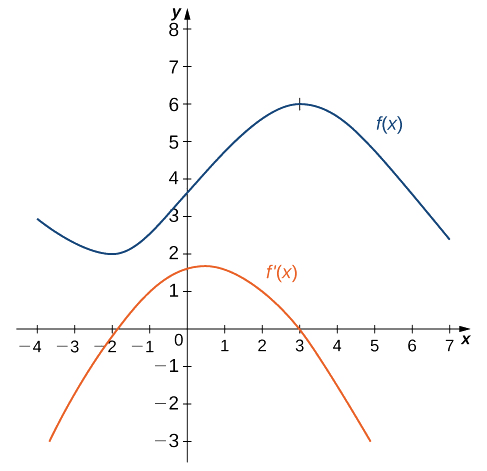
Використовуйте наступний графік,\(f(x)\) щоб намалювати графік\(f'(x)\).
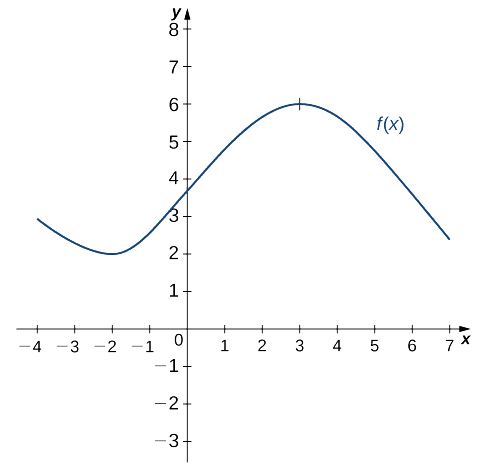
Рішення
Рішення наведено на наступному графіку. Спостерігайте,\(f(x)\) що збільшується і\(f'(x)>0\) далі\((–2,3)\). Також,\(f(x)\) зменшується і\(f'(x)<0\) далі,\((−∞,−2)\) і далі\((3,+∞)\). Також зверніть увагу, що\(f(x)\) має горизонтальні дотичні в\(–2\) і\(3\),\(f'(−2)=0\) і\(f'(3)=0\).
Намалюйте графік\(f(x)=x^2−4\). На якому інтервалі знаходиться графік\(f'(x)\) вище\(x\) -осі?
- Підказка
-
Графік\(f'(x)\) позитивний, де\(f(x)\) збільшується.
- Відповідь
-
\((0,+∞)\)
Похідні та безперервність
Тепер, коли ми можемо графікувати похідну, давайте розглянемо поведінку графіків. Спочатку розглянемо зв'язок між диференційованістю і безперервністю. Ми побачимо, що якщо функція диференційована в точці, вона повинна бути безперервною там; однак функція, яка є безперервною в точці, не повинна бути диференційованою в цій точці. Насправді функція може бути безперервною в точці і не може бути диференційованою в точці з однієї з кількох причин.
\(f(x)\)Дозволяти бути функцією і\(a\) бути в її області. Якщо\(f(x)\) диференційована при\(a\),\(f\) то безперервна при\(a\).
Якщо\(f(x)\) диференціюється в\(a\), то\(f'(a)\) існує і, якщо ми дозволимо\(h = x - a\), ми маємо\( x = a + h \), і як\(h=x-a\to 0\), ми можемо бачити, що\(x\to a\).
Тоді
\[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber \]
можна переписати як
\(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\).
Ми хочемо показати, що\(f(x)\) це безперервно,\(a\) показуючи, що\(\displaystyle \lim_{x→a}f(x)=f(a).\) Таким чином,
\ (\ почати {вирівнювати*}\ стиль відображення\ lim_ {x → a} f (x) &=\ lim_ {x → a}\;\ великий (f (x) −f (a) +f (a)\ великий)\\ [4pt]
&=\ lim_ {x → a}\ ліворуч (\ frac {f (x) −f (a)} {x−a} (x−a) +f (a)\ праворуч) &\ text {Множення та ділення} (f (x) −f (a))\ текст {на} x−a.\\ [4pt]
&=\ ліворуч (\ lim_ {x→a}\ frac {f (x) −f (a)} {x−a}\ праворуч) ⋅ ліворуч (\ lim_ {x→a}\; (x−a)\ праворуч) +\ lim_ {x→a} f (a)\\ [4pt]
&=f' (a) ⋅0+f (a)\\ [4pt]
&=f (a). \ end {вирівнювати*}\)
Тому, оскільки\(f(a)\) визначається і\(\displaystyle \lim_{x→a}f(x)=f(a)\), ми робимо висновок, що\(f\) є безперервним при\(a\).
□
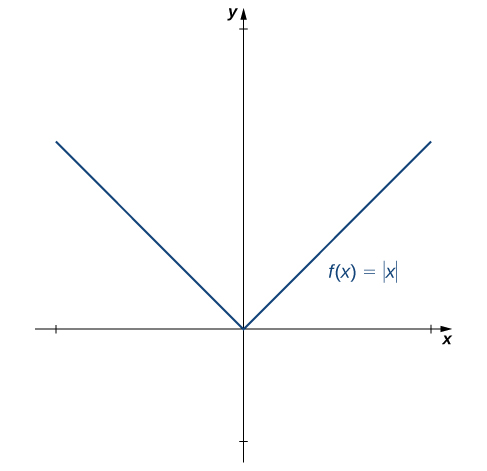
Ми щойно довели, що диференційовність передбачає безперервність, але тепер ми розглянемо, чи означає безперервність диференційованість. Щоб визначити відповідь на це питання, вивчимо функцію\(f(x)=|x|\). Ця функція є безперервною скрізь; однак,\(f'(0)\) не визначена. Це спостереження змушує нас вважати, що безперервність не передбачає диференційованості. Давайте досліджуємо далі. Для\(f(x)=|x|\),
\(f'(0)=\displaystyle \lim_{x→0}\frac{f(x)−f(0)}{x−0}= \lim_{x→0}\frac{|x|−|0|}{x−0}= \lim_{x→0}\frac{|x|}{x}\).
Цей ліміт не існує, оскільки
\(\displaystyle \lim_{x→0^−}\frac{|x|}{x}=−1\)і\(\displaystyle \lim_{x→0^+}\frac{|x|}{x}=1\).
Див\(\PageIndex{4}\). Малюнок.
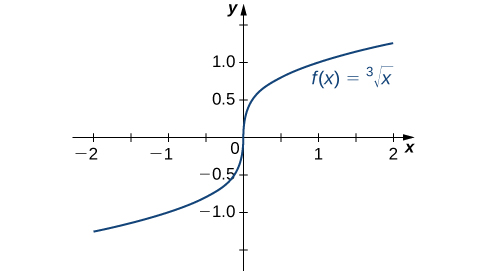
Розглянемо деякі додаткові ситуації, в яких безперервна функція не може бути диференційованою. Розглянемо функцію\(f(x)=\sqrt[3]{x}\):
\(f'(0)=\displaystyle \lim_{x→0}\frac{\sqrt[3]{x}−0}{x−0}=\displaystyle \lim_{x→0}\frac{1}{\sqrt[3]{x^2}}=+∞\).
Таким чином\(f'(0)\) не існує. Швидкий погляд на графік\(f(x)=\sqrt[3]{x}\) прояснює ситуацію. Функція має вертикальну дотичну лінію на\(0\) (рис.\(\PageIndex{5}\)).
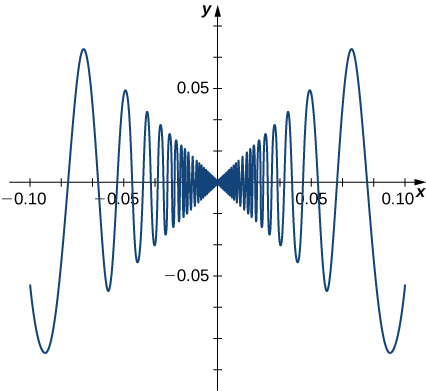
Функція\(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & & \text{ if } x=0\end{cases}\) також має похідну, яка проявляє цікаву поведінку при\(0\).
Ми бачимо, що
\(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/x\right)−0}{x−0}= \lim_{x→0}\sin\left(\frac{1}{x}\right)\).
Ця межа не існує, по суті тому, що нахили січних ліній безперервно змінюють напрямок у міру наближення до нуля (рис.\(\PageIndex{6}\)).
Підсумовуючи:
- Ми спостерігаємо, що якщо функція не є безперервною, вона не може бути диференційованою, оскільки кожна диференційована функція повинна бути безперервною. Однак, якщо функція є безперервною, вона все одно може не бути диференційованою.
- Ми побачили, що\(f(x)=|x|\) не вдалося диференціюватися в\(0\) тому, що межа нахилів дотичних ліній зліва і справа не були однаковими. Візуально це призвело до гострого кута на графіку функції в\(0.\) З цього ми робимо висновок, що для того, щоб бути диференційованим у точці, функція повинна бути «гладкою» в цій точці.
- Як ми бачили в прикладі\(f(x)=\sqrt[3]{x}\), функція не може бути диференційованою в точці, де є вертикальна дотична лінія.
- Як ми бачили\(f(x)=\begin{cases}x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & &\text{ if } x=0\end{cases}\) з функцією, може не бути диференційованим у точці більш складними способами.
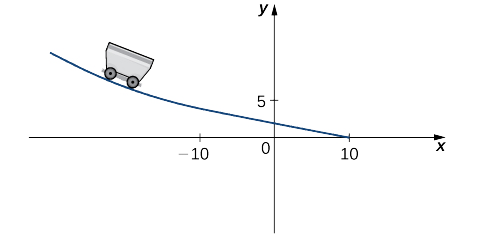
Іграшкова компанія хоче спроектувати трек для іграшкового автомобіля, який починається вздовж параболічної кривої, а потім перетворюється на пряму лінію (рис.\(\PageIndex{7}\)). Функція, яка описує трек, полягає в тому, щоб мати форму\(f(x)=\begin{cases}\frac{1}{10}x^2+bx+c, & & \text{ if }x<−10\\−\frac{1}{4}x+\frac{5}{2}, & & \text{ if } x≥−10\end{cases}\), де\(x\) і\(f(x)\) знаходяться в дюймах. Щоб автомобіль плавно рухався по трасі, функція\(f(x)\) повинна бути як безперервною, так і диференційованою при\(−10\). Знайдіть значення\(b\) і\(c\) які роблять\(f(x)\) як безперервними, так і диференційованими.
Рішення
Щоб функція була безперервною при\(x=−10\),\(\displaystyle \lim_{x→10^−}f(x)=f(−10)\). Таким чином, так як
\(\displaystyle \lim_{x→−10^−}f(x)=\frac{1}{10}(−10)^2−10b+c=10−10b+c\)
і\(f(−10)=5\), ми повинні мати\(10−10b+c=5\). Аналогічно, у нас є\(c=10b−5\).
Щоб функція була диференційована при\(−10\),
\(f'(10)=\displaystyle \lim_{x→−10}\frac{f(x)−f(−10)}{x+10}\)
повинні існувати. Оскільки\(f(x)\) визначається за допомогою різних правил праворуч і ліворуч, ми повинні оцінити цю межу справа і зліва, а потім встановити їх рівними один одному:
\ (\ стиль відображення\ почати {вирівнювати*}\ lim_ {x→−10^−}\ розрив {f (x) −f (−10)} {x+10} &=\ lim_ {x →−10^−}\ frac {\ frac {1} {10} x^2+bx+c−5} {x+10}\ [4pt]
&=\ lim _ {x→−10^−}\ розрив {\ розриву {1} {10} x^2+bx+ (10b−5) −5} {x+10} &\ текст {Заміна} c=10b−5.\\ [4pt]
&=\ lim_ {x→−10^−}\ frac {x^2−100+10bx+ 100b} {10 (x+10)}\\ [4pt]
&=\ lim_ {x→−10^−}\ розрив {(x+10) (x−10+10b)} {10 (x+10)} &\ текст {Фактор за групуванням}\\ [4pt]
&=b−2\ end {align*}\).
У нас також є
\ (\ стиль відображення\ почати {вирівнювати*}\ lim_ {x→−10^+}\ розрив {f (x) −f (−10)} {x+10} &=\ lim_ {x→−10^+}\ frac {−\ frac {1} {4} x+\ frac {5} {2} −5} {x+10}\ [4pt]
&=\ lim_ {x→−10^+}\ розрив {− (x+10)} {4 (x+10)}\\ [4pt]
&=−\ розрив {1} {4}\ end {align*}\).
Це дає нам\(b−2=−\frac{1}{4}\). Таким чином\(b=\frac{7}{4}\) і\(c=10(\frac{7}{4})−5=\frac{25}{2}\).
Знайти значення a і b, які роблять\(f(x)=\begin{cases}ax+b, & & \text{ if } x<3\\x^2, & & \text{ if } x≥3\end{cases}\) як неперервними, так і диференційованими при\(3\).
- Підказка
-
Використовуйте\(\PageIndex{4}\) Example як орієнтир.
- Відповідь
-
\(a=6\)і\(b=−9\)
Похідні для вищого порядку
Похідна функції сама по собі є функцією, тому ми можемо знайти похідну від похідної. Наприклад, похідна функції положення - це швидкість зміни положення, або швидкість. Похідна швидкості - це швидкість зміни швидкості, яка є прискоренням. Нова функція, отримана при диференціації похідної, називається другою похідною. Крім того, ми можемо продовжувати приймати похідні для отримання третьої похідної, четвертої похідної тощо. У сукупності їх називають похідними вищого порядку. Позначення для похідних вищого порядку\(y=f(x)\) може бути виражено в будь-якій з наступних форм:
\(f''(x),\; f'''(x),\; f^{(4)}(x),\; …\; ,\; f^{(n)}(x)\)
\(y''(x),\; y'''(x),\; y^{(4)}(x),\; …\; ,\; y^{(n)}(x)\)
\(\dfrac{d^2y}{dx^2},\;\dfrac{d^3y}{dy^3},\;\dfrac{d^4y}{dy^4},\;…\;,\;\dfrac{d^ny}{dy^n}.\)
Цікаво відзначити, що позначення для\(\dfrac{d^2y}{dx^2}\) можна розглядати як спробу висловити\(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\) більш компактно.
Аналогічно,\(\dfrac{d}{dx}\left(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\right)=\dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right)=\dfrac{d^3y}{dx^3}\).
Для\(f(x)=2x^2−3x+1\), знайдіть\(f''(x)\).
Рішення
Перша знахідка\(f'(x)\).
\(f(x)=2x^2−3x+1\)\(f(x+h)=2(x+h)^2−3(x+h)+1\)Замінюємо і в\(f'(x)=\displaystyle \lim_{h→0}\dfrac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle \lim_{h→0}\frac{(2(x+h)^2−3(x+h)+1)−(2x^2−3x+1)}{h}\) | |
| \(=\displaystyle \lim_{h→0}\frac{4xh+2h^2−3h}{h}\) | Спростити чисельник. |
| \(=\displaystyle \lim_{h→0}(4x+2h−3)\) | Коефіцієнт\(h\) в чисельнику і скасувати зі знаменником\(h\) в. |
| \(=4x−3\) | Візьміть ліміт. |
Далі знаходимо,\(f''(x)\) взявши похідну від\(f'(x)=4x−3.\)
| \(f''(x)=\displaystyle \lim_{h→0}\frac{f'(x+h)−f'(x)}{h}\) | \(f ′(x)\)Використовувати\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\) з замість\(f(x).\) |
| \(=\displaystyle \lim_{h→0}\frac{(4(x+h)−3)−(4x−3)}{h}\) | Замінник\(f'(x+h)=4(x+h)−3\) і\(f'(x)=4x−3.\) |
| \(=\displaystyle \lim_{h→0}4\) | Спростити. |
| \(=4\) | Візьміть ліміт. |
Знайти\(f''(x)\) для\(f(x)=x^2\).
- Підказка
-
Ми знайшли\(f'(x)=2x\) в попередньому контрольно-пропускному пункті. Використовуйте рівняння\ ref {derdef}, щоб знайти похідну від\(f'(x)\)
- Відповідь
-
\(f''(x)=2\)
Положення частинки вздовж осі координат в часі\(t\) (у секундах) задається\(s(t)=3t^2−4t+1\) (у метрах). Знайдіть функцію, яка описує її прискорення в часі\(t\).
Рішення
Починаючи з\(v(t)=s′(t)\) і\(a(t)=v′(t)=s''(t)\), ми починаємо з знаходження похідної від\(s(t)\):
\ (\ стиль відображення\ почати {вирівнювати*} s′ (t) &=\ lim_ {h → 0}\ frac {s (t+h) −s (t)} {h}\ [4pt]
&=\ lim_ {h → 0}\ frac {3 (t+h) ^2−4 (t+h) +1− (3t^2−4t+1}) {h}\\ [4pt]
&=6t−4. \ end {вирівнювати*}\)
Далі,
\ (\ стиль відображення\ почати {вирівнювати*} s "(t) &=\ lim_ {h → 0}\ frac {s′ (t+h) −s′ (t)} {h}\ [4pt]
&=\ lim_ {h → 0}\ frac {6 (t+h) −4 − (6t−4)} {h}\ [4pt]
= 6. \ end {вирівнювати*}\)
Таким чином,\(a=6 \;\text{m/s}^2\).
Для\(s(t)=t^3\), знайдіть\(a(t).\)
- Підказка
-
Використовуйте\(\PageIndex{6}\) Example як орієнтир.
- Відповідь
-
\(a(t)=6t\)
Ключові концепції
- Похідна функції\(f(x)\) - це функція, значення якої at\(x\) дорівнює\(f'(x)\).
- Графік похідної функції\(f(x)\) пов'язаний з графом\(f(x)\). Де\(f(x)\) має дотичну лінію з додатним нахилом,\(f'(x)>0\). Де\(f(x)\) має дотичну лінію з негативним нахилом,\(f'(x)<0\). Де\(f(x)\) має горизонтальну дотичну лінію,\(f'(x)=0.\)
- Якщо функція диференційована в точці, то вона є безперервною в цій точці. Функція не диференційована в точці, якщо вона не є безперервною в точці, якщо вона має вертикальну дотичну лінію в точці, або якщо графік має гострий кут або кут.
- Похідні вищого порядку - це похідні від похідних, від другої похідної до\(n^{\text{th}}\) похідної.
Ключові рівняння
- похідна функція
\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)
Глосарій
- похідна функція
- дає похідну функції в кожній точці області початкової функції, для якої визначено похідну
- диференційований при\(a\)
- функція, для якої\(f'(a)\) існує, диференційовна при\(a\)
- диференційований на\(S\)
- функція, для якої\(f'(x)\) існує для кожного\(x\) у відкритому\(S\) множині, диференційована на\(S\)
- диференційована функція
- функція, для якої\(f'(x)\) існує, є диференційовною функцією
- похідна вищого порядку
- похідна похідної, від другої похідної до\(n^{\text{th}}\) похідної, називається похідною вищого порядку
Автори та атрибуція
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added explanation of the alternative definition of the derivative used in the proof of that differentiability implies continuity.
