8.4: Умовна ймовірність

Last updated
Save as PDF

Page ID: 67072

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

У цьому розділі ви навчитеся:

визнати ситуації, пов'язані з умовною ймовірністю
обчислити умовні ймовірності

Припустимо, друг запитує у вас ймовірність того, що сьогодні піде сніг.

Якщо ви перебуваєте в Бостоні, штат Массачусетс взимку, ймовірність снігу сьогодні може бути досить істотною. Якщо влітку ви перебуваєте в Купертіно, Каліфорнія, ймовірність снігу сьогодні дуже крихітна, ця ймовірність майже 0.

Нехай:

$\mathrm{A}$= подія, що сьогодні буде сніг
$\mathrm{B}$= подія, що сьогодні ви перебуваєте в Бостоні в зимовий час
$\mathrm{C}$= подія, що сьогодні ви перебуваєте в Купертіно влітку

Оскільки на ймовірність снігу впливає місце і час року, ми не можемо просто написати$\mathrm{P(A)}$ для ймовірності снігу. Нам потрібно вказати іншу інформацію, яку ми знаємо -місце і час року. Потрібно використовувати умовну ймовірність.

Захід, який нас цікавить, - це подія$\mathrm{A}$ для снігу. Інша подія називається умовою, що представляє місце і час року в даному випадку.

Ми представляємо умовну ймовірність, використовуючи вертикальну лінію | що означає «якщо», або «враховуючи, що», або «якщо ми це знаємо». Цікава подія з'являється зліва від |. Стан з'являється на правій стороні |.

Імовірність снігу, враховуючи, що (якщо) ви перебуваєте в Бостоні взимку представлена$\mathbf{P} \left( \mathbf{A} | \mathbf{B}\right) $. В даному випадку умова є$\mathrm{B}$.

Імовірність того, що буде сніг, враховуючи, що (якщо) ви перебуваєте в Купертіно влітку, представлена$\mathbf{P}(\mathbf{A} | \mathbf{C})$. В даному випадку умова є$\mathrm{C}$.

Тепер давайте розберемо ситуацію, коли ми можемо обчислити деякі ймовірності.

Припустимо, ви з другом граєте в гру, яка передбачає вибір однієї карти з добре перетасованої колоди. Ваш друг роздає вам одну карту, обличчям вниз, з колоди і пропонує вам наступну угоду: Якщо карта є королем, він заплатить вам 5 доларів, інакше ви заплатите йому 1 долар. Ви повинні грати в гру?

Ви міркуєте наступним чином. Так як в колоді чотири короля, ймовірність отримання короля дорівнює 4/52 або 1/13. Отже, ймовірність не отримати короля дорівнює 12/13. Це означає, що співвідношення вашого виграшу до програшу становить 1 до 12, тоді як коефіцієнт виплат становить лише 1 до 5 доларів. Тому ви визначаєте, що грати не варто.

Але розглянемо наступний сценарій розвитку подій. Поки ваш друг роздавав карту, вам довелося отримати погляд на неї і помітили, що карта була лицьовою карткою. Чи повинні ви зараз грати в гру?

Оскільки в колоді 12 лицьових карт, то загальні елементи в просторі зразка вже не 52, а всього 12. Це означає, що шанс отримати короля дорівнює 4/12 або 1/3. Таким чином, ваш шанс на перемогу становить 1/3 і втратити 2/3. Це робить ваш виграш до втрати співвідношення 1 до 2, який тарифи набагато краще з коефіцієнтом виплат від $1 до $5. Цього разу ви визначаєте, що вам слід грати.

У другій частині наведеного вище прикладу ми знаходили ймовірність отримання короля, знаючи, що карта обличчя показала. Це приклад умовної ймовірності. Всякий раз, коли ми знаходимо ймовірність події за$\mathrm{E}$ умови, що$\mathrm{F}$ сталася інша подія, ми знаходимо умовну ймовірність.

Символ$\mathrm{P(E | F)}$ позначає проблему знаходження ймовірності$\mathrm{E}$ даного, що$\mathrm{F}$ сталося. Читаємо$\mathrm{P(E | F)}$ як «ймовірність$\mathrm{E}$, дана»$\mathrm{F}$.

Приклад$\PageIndex{1}$

У сім'ї троє дітей. Знайдіть умовну ймовірність народження двох хлопчиків і дівчинки, враховуючи, що первісток - це хлопчик.

Рішення

Нехай подією$\mathrm{E}$ буде те, що в родині двоє хлопчиків і дівчинка, і$\mathrm{F}$ що первісток - хлопчик.

Спочатку ми вибираємо простір для сім'ї з трьох дітей наступним чином.

\[S = \{BBB, BBG, BGB, BGG, GBB, GBG, GGB, GGG\} \nonumber \]

Оскільки ми знаємо, що перший народився хлопчик, наші можливості звужуються до чотирьох результатів: BBB, BBG, BGB та BGG.

Серед чотирьох BBG і BGB представляють двох хлопчиків і дівчинку.

Тому$\mathrm{P(E | F)}$ = 2/4 або 1/2.

Приклад$\PageIndex{2}$

Одна шестистороння матриця прокатується один раз.

Знайдіть ймовірність того, що результат буде рівним.
Знайдіть ймовірність того, що результат навіть дається, що результат більше трьох.

Рішення

Простір зразка$\mathrm{S} = {1,2,3,4,5,6}$

Нехай подією$\mathrm{E}$ буде те, що результат рівний і$\mathrm{T}$ бути, що результат більше 3.

а.$\mathrm{P(E)}$ = 3/6 тому що$\mathrm{E} = {2,4,6}$

б. тому що ми знаємо$T = {4,5,6}$, що 1, 2, 3 не може статися; можливі лише результати 4, 5, 6. Тому з значень в$\mathrm{E}$ можливі лише 4, 6.

Тому$\mathrm{P(E|T)}$ = 2/3

Приклад$\PageIndex{3}$

Справедлива монета кидається двічі.

Знайдіть ймовірність того, що в результаті вийде дві головки.
Знайдіть ймовірність того, що в результаті вийде дві головки, враховуючи, що виходить хоча б одна голова.

Рішення

Простір зразка $S = {HH, HT, TH, TT}$

Нехай подією$\mathrm{E}$ буде те, що дві головки вийшли і$\mathrm{F}$ вийде хоча б одна голова.

a.$\mathrm{P(E)}$ = 1/4 тому що$\mathrm{E} = {HH}$ і простір вибірки$\mathrm{S}$ має 4 результати.

б$\mathrm{F} = {HH, HT, TH}$. Так як була отримана хоча б одна головка, ТТ не виникло.
Нас цікавить подія ймовірності$\mathrm{E}={HH}$ з 3 результатів у скороченому просторі вибірки F.

Тому$\mathrm{P(E|F)}$ = 1/3

Розробимо тепер формулу умовної ймовірності$\mathrm{P(E | F)}$.

Припустимо, експеримент складається з$n$ однаково ймовірних подій. Далі припустимо, що є$m$ елементи в$\mathrm{F}$, і$c$ елементи в$\mathrm{E} \cap \mathrm{F}$, як показано на наступній діаграмі Венна.

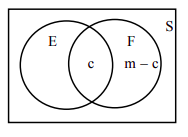
$Розділ 8.4 PNG$

Якщо подія$\mathrm{F}$ відбулася, набір усіх можливих результатів - це вже не весь простір вибірки, а натомість підмножина$\mathrm{F}$. Тому ми дивимося лише на набір$\mathrm{F}$ і нічого поза$\mathrm{F}$. Так як$\mathrm{F}$ має$m$ елементи, то знаменник при обчисленні$\mathrm{P(E | F)}$ є$m$. Ми можемо подумати, що чисельником нашої умовної ймовірності є кількість елементів в$\mathrm{E}$. Але очевидно, що ми не можемо розглядати елементи$\mathrm{E}$, яких немає в$\mathrm{F}$. Ми можемо лише порахувати елементи,$\mathrm{E}$ що знаходяться в$\mathrm{F}$, тобто елементи в$\mathrm{E} \cap \mathrm{F}$. Тому

\[\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{c}}{\mathrm{m}} \nonumber \]

Розділивши і чисельник, і знаменник на$n$, отримаємо

\[\mathrm{P(E | F)}=\frac{c / n}{m / n} \nonumber \]

Але$c/n = \mathrm{P}(\mathrm{E} \cap \mathrm{F})$, і$m/n = \mathrm{P}(\mathrm{F})$.

Підставляючи, виведемо наступну формулу для$\mathrm{P}(\mathrm{E} | \mathrm{F})$.

Правило умовної ймовірності

Для двох подій$\mathrm{E}$$\mathrm{F}$ і ймовірність «$\mathrm{E}$заданого$\mathrm{F}$» дорівнює

\[\mathbf{P}(\mathbf{E} | \mathbf{F})=\frac{\mathbf{P}(\mathbf{E} \cap \mathbf{F})}{\mathbf{P}(\mathbf{F})} \nonumber \]

Приклад$\PageIndex{4}$

Прокочується одинарна плашка. Використовуйте наведену вище формулу, щоб знайти умовну ймовірність отримання парного числа, враховуючи, що число більше трьох показало.

Рішення

$\mathrm{E}$Дозволяти подія, що парне число показує, і$\mathrm{F}$ бути подією, що число більше трьох показує. Ми хочемо$\mathrm{P}(\mathrm{E} | \mathrm{F})$.

$\mathrm{E} = {2, 4, 6}$і$\mathrm{F} = {4, 5, 6}$. Що означає,$\mathrm{E} \cap \mathrm{F} = { 4, 6}$

Тому$\mathrm{P}(\mathrm{F})$ = 3/6, а$\mathrm{P}(\mathrm{E} \cap \mathrm{F})$ = 2/6

\[P(E | F)=\frac{P(E \cap F)}{P(F)}=\frac{2 / 6}{3 / 6}=\frac{2}{3} \nonumber. \nonumber \]

Приклад$\PageIndex{5}$

Наступна таблиця показує розподіл за статтю студентів у громадському коледжі, які їздять на громадському транспорті, та тих, хто їде до школи.

	Чоловічий (M)	Жіночий (F)	Всього
Громадський транспорт (T)	8	13	21
Привід (D)	39	40	79
Всього	47	53	100

Події$\mathrm{M}, \mathrm{F}, \mathrm{T}$, і самі$\mathrm{D}$ за себе пояснюються. Знайдіть наступні ймовірності.

$\mathrm{P}(\mathrm{D} | \mathrm{M})$
$\mathrm{P}(\mathrm{F} | \mathrm{D})$
$\mathrm{P}(\mathrm{M} | \mathrm{T})$

Рішення 1

Умовні ймовірності часто можна знайти безпосередньо з таблиці надзвичайних ситуацій. Якщо умова відповідає тільки одному рядку або тільки одному стовпчику в таблиці, то можна ігнорувати решту таблиці і прочитати умовну ймовірність прямо з рядка або стовпця, зазначеного умовою.

Умова - подія$\mathrm{M}$; ми можемо подивитися тільки стовпець «Чоловік» таблиці та ігнорувати решту таблиці:$\mathrm{P}(\mathrm{D} | \mathrm{M})=\frac{39}{47}$.
Умовою є подія$\mathrm{D}$; ми можемо подивитися тільки рядок «Drive» таблиці і ігнорувати решту таблиці:$\mathrm{P}(\mathrm{F} | \mathrm{D})=\frac{40}{79}$.
Умова - подія$\mathrm{T}$; ми можемо подивитися тільки рядок «Громадський транспорт» таблиці та ігнорувати решту таблиці:$\mathrm{P}(\mathrm{M} | \mathrm{T})=\frac{8}{21}$.

Рішення 2

Використовуємо формулу умовної ймовірності$\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P(F)}}$.

\[P(D | M)=\frac{P(D \cap M)}{P(M)}=\frac{39 / 100}{47 / 100}=\frac{39}{47} \nonumber . \nonumber \]
\[P(F | D)=\frac{P(F \cap D)}{P(D)}=\frac{40 / 100}{79 / 100}=\frac{40}{79} \nonumber . \nonumber \]
\[\mathrm{P}(\mathrm{M} | \mathrm{T})=\frac{P(M \cap T)}{P(T)}=\frac{8 / 100}{21 / 100}=\frac{8}{21} \nonumber \]

Приклад$\PageIndex{6}$

Дано$\mathrm{P(E)}$ = .5,$\mathrm{P}(\mathrm{F})$ = .7, і$\mathrm{P}(\mathrm{E} \cap \mathrm{F})$ = .3. Знайдіть наступне:

$\mathrm{P}(\mathrm{E} | \mathrm{F})$
$\mathrm{P}(\mathrm{F} | \mathrm{E})$

Рішення

Використовуємо формулу умовної ймовірності.

$P(E | F)=\frac{P(E \cap F)}{P(F)}=\frac{3}{7}=\frac{3}{7}$
$P(F | E)=\frac{P(E \cap F)}{P(E)}=.3 / .5=3 / 5 $

Приклад$\PageIndex{7}$

$\mathrm{E}$і$\mathrm{F}$ є взаємовиключними подіями такими, що$\mathrm{P(E)}$ = .4,$\mathrm{P(F)}$ = .9. Знайти$\mathrm{P(E | F)}$.

Рішення

$\mathrm{E}$і$\mathrm{F}$ є взаємовиключними, тому$\mathrm{P}(\mathrm{E} \cap \mathrm{F})$ = 0.
Тому$\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}=\frac{0}{9}=0$.

Приклад$\PageIndex{8}$

Дано$\mathrm{P}(\mathrm{F} | \mathrm{E})$ = .5, і$\mathrm{P}(\mathrm{E} \cap \mathrm{F})$ = .3. Знайти$\mathrm{P}(\mathrm{E})$.

Рішення

Використовуючи формулу умовної ймовірності$\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}$, отримаємо

\[\mathrm{P}(\mathrm{F} | \mathrm{E})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{E})} \nonumber \]

Заміна та рішення:

\[.5=\frac{.3}{\mathrm{P}(\mathrm{E})} \quad \text { or } \quad \mathrm{P}(\mathrm{E})=3 / 5 \nonumber \]

Приклад$\PageIndex{9}$

У сім'ї з трьох дітей знайдіть умовну ймовірність народження двох хлопчиків і дівчинки, враховуючи, що в сім'ї є не менше двох хлопчиків.

Рішення

Нехай подією$\mathrm{E}$ буде те, що в родині двоє хлопчиків і дівчинка, і нехай$\mathrm{F}$ буде ймовірність того, що в сім'ї є не менше двох хлопчиків. Ми хочемо$\mathrm{P}(\mathrm{E} | \mathrm{F})$.

Перерахуємо зразок простору разом з подіями$\mathrm{E}$ і$\mathrm{F}$.

\ begin {вирівняний}
&\ математика {S} =\ {\ математика {BBB},\ математика {BBG},\ математика {BGB},\ математика {GBG},\ математика {GBG},\ математика {GBG},\ математика {GBG},\ математика {GGB}\
Therm {E} =\ {\ математика {BBG},\ математика {BGB},\ математика {ГББ}\}\ текст {і}\ математика {F} =\ {\ математика {BBB},\ математика {BBB},\ математика {BGB},\ математика {GBB}\\\
&\ математика {E}\ cap\ математика {F} =\ {\ математика {BBG},\ математика {BGB},\ математика {GBB}
\ кінець {вирівняний}

Тому$\mathrm{P}(\mathrm{F})$ = 4/8, а$\mathrm{P}(\mathrm{E} \cap \mathrm{F})$ = 3/8, а

\[\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{E})} =\frac{3/8}{4/8} =\frac{3}{4} \nonumber. \nonumber \]

Приклад$\PageIndex{10}$

У коледжі 65% студентів підписуються на Amazon Prime, 50% підписуються на Netflix, а 20% підписуються на обидва. Якщо студент обраний навмання, знайдіть такі ймовірності:

студент підписується на Amazon Prime, враховуючи, що він підписується на Netflix
студент підписується на Netflix, враховуючи, що він підписується на Amazon Prime

Рішення

Нехай$\mathrm{A}$ буде подія, коли студент підписується на Amazon Prime, і$\mathrm{N}$ буде подією, яку студент підписується на Netflix.

Спочатку визначте ймовірності та події, наведені в проблемі.

$\mathrm{P}$(студент підписується на Amazon Prime)$\mathrm{P(A)}$ = 0,65

$\mathrm{P}$(студент підписується на Netflix)$\mathrm{P(N)}$ = 0,50

$\mathrm{P}$(студент підписується як на Amazon Prime, так і на Netflix)$\mathrm{P(A \cap N)}$ = = 0,20

Тоді скористайтеся правилом умовної ймовірності:

$\mathrm{P}(\mathrm{A} | \mathrm{N})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{N})}{\mathrm{P}(\mathrm{N})} = \frac{.20}{.50} = \frac{2}{5}$
$\mathrm{P}(\mathrm{N} | \mathrm{A})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{N})}{\mathrm{P}(\mathrm{A})} = \frac{.20}{.65} = \frac{4}{13}$

Цілі навчання

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Правило умовної ймовірності

Приклад\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\)

Приклад\(\PageIndex{7}\)

Приклад\(\PageIndex{8}\)

Приклад\(\PageIndex{9}\)

Приклад\(\PageIndex{10}\)