10.4: Підрахунок
- Page ID
- 66532
Підрахунок? Ви вже знаєте, як рахувати, або ви не будете приймати клас математики на рівні коледжу, чи не так? Ну так, але те, що ми дійсно будемо досліджувати тут способи ефективного підрахунку. Коли ми перейдемо до ймовірних ситуацій трохи пізніше в цьому розділі, нам потрібно буде підрахувати деякі дуже великі числа, наприклад кількість можливих виграшних лотерейних квитків. Одним із способів зробити це було б записати всі можливі набори чисел, які можуть з'явитися на лотерейному квитку, але повірте мені: ви не хочете цього робити.
Основний підрахунок
Ми почнемо, однак, з деяких більш розумних видів підрахунку проблем, щоб розробити ідеї, які нам скоро знадобляться.
Припустимо, в певному ресторані у вас є три варіанти закуски (суп, салат або хлібні палички) і п'ять варіантів для основної страви (гамбургер, бутерброд, кіш, фахіта або піца). Якщо вам дозволено вибрати саме один пункт з кожної категорії для вашої їжі, скільки різних варіантів їжі у вас є?
Рішення
Рішення 1: Одним із способів вирішення цієї проблеми було б систематично перераховувати кожен можливий прийом їжі:
| суп + гамбургер | суп+бутерброд | суп + кіш |
| суп + фахіта | суп+піца | салат + гамбургер |
| салат+бутерброд | салат + кіш | салат + фахіта |
| салат + піца | хлібні палички-гамбургер | хлібні палички+сендві |
| хлібні палички+кіш | хлібні палички + фахіта | хлібні палички+піца |
Припускаючи, що ми робили це систематично і що ми не пропускали жодних можливостей і не перераховували жодної можливості більше одного разу, відповідь буде 15. Таким чином, ви можете піти в ресторан 15 ночей поспіль і щовечора по-різному поїсти.
Рішення 2. Іншим способом вирішення цієї проблеми було б перерахувати всі можливості в таблиці:
| гамбургер | сендвіч | кіш | фахіта | піца | |
| суп | суп + бургер | ||||
| салат | салат + бургер | ||||
| хліб | і т.д. |
У кожній з комірок таблиці ми могли б перерахувати відповідну їжу: суп+гамбургер у верхньому лівому куті, салат+гамбургер під ним тощо Але якби нас насправді не хвилювало, що таке можливі страви, лише скільки можливих страв є, ми могли б просто порахувати кількість клітин і прийти до відповіді 15, що відповідає нашій відповіді з першого рішення. (Це завжди добре, коли ви вирішуєте проблему двома різними способами і отримуєте однакову відповідь!)
Рішення 3: У нас вже є два ідеально хороших рішення. Навіщо потрібна третя? Перший метод був не дуже систематичним, і ми могли б легко зробити упущення. Другий спосіб був кращим, але припустимо, що окрім закуски та основної страви ми ще більше ускладнили проблему, додаючи десерти в меню: ми використовували рядки столу для закусок і стовпчики для основних страв - куди підуть десерти? Нам знадобиться третій вимір, і оскільки малювання 3-D таблиць на 2-D сторінці або екрані комп'ютера не дуже просто, нам потрібен кращий спосіб у випадку, якщо у нас є три категорії, щоб вибрати форму замість двох.
Отже, повернемося до проблеми в прикладі. Що ще ми можемо зробити? Намалюємо діаграму дерева:
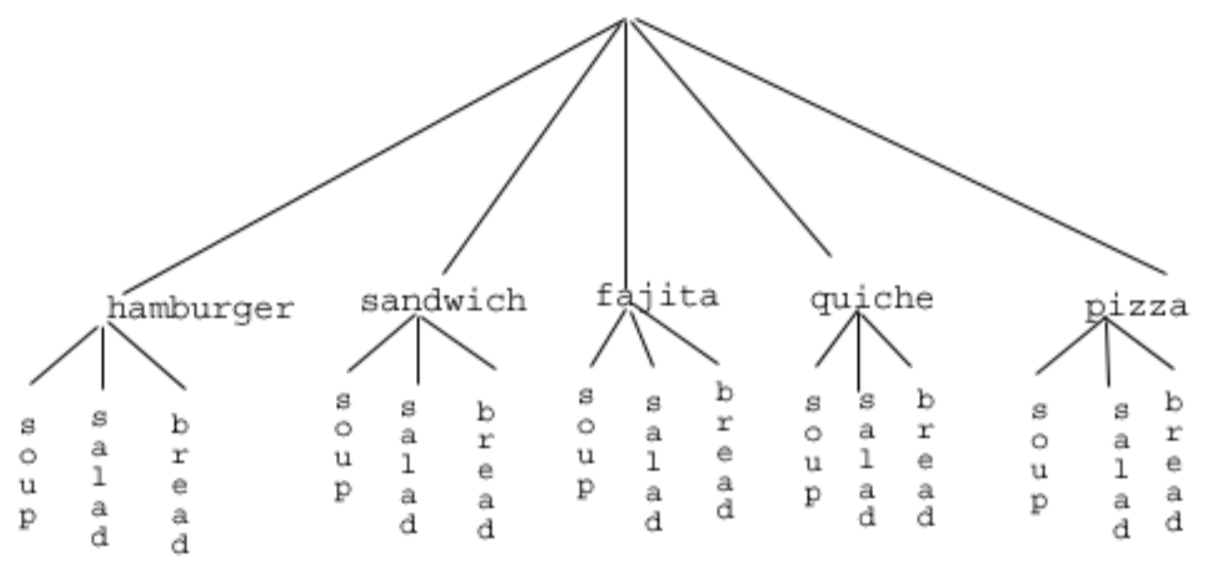
Це називається діаграмою «дерева», тому що на кожному етапі ми розгалужуємося, як гілки на дереві. У цьому випадку ми спочатку намалювали п'ять гілок (по одній на кожну основну страву), а потім для кожної з цих гілок намалювали ще три гілки (по одній на кожну закуску). Підраховуємо кількість гілок на фінальному рівні і отримуємо (сюрприз, сюрприз!) 15.
Якби ми хотіли, ми могли б замість цього намалювати три гілки на першому етапі для трьох закусок, а потім п'ять гілок (по одній для кожної основної страви), що розгалужуються з кожної з цих трьох гілок.
Добре, так що тепер ми знаємо, як рахувати можливості за допомогою таблиць і діаграм дерева. Ці методи і надалі будуть корисні в певних випадках, але уявіть собі гру, де у вас є дві колоди карт (з 52 карти в кожній колоді) і ви вибираєте по одній карті з кожної колоди. Ви дійсно хочете намалювати таблицю або діаграму дерева, щоб визначити кількість результатів цієї гри?
Давайте повернемося до попереднього прикладу, який передбачав вибір страви з трьох закусок і п'яти основних страв, і подивимося на друге рішення, яке використовувало стіл. Зверніть увагу, що одним із способів підрахунку кількості можливих прийомів їжі є просто пронумерація кожної з відповідних клітин в таблиці, як ми зробили вище. Але ще одним способом підрахунку кількості осередків у таблиці було б помножити кількість рядків (3) на кількість стовпців (5), щоб отримати 15. Зверніть увагу, що ми могли б прийти до того ж результату, не роблячи стіл взагалі, просто помноживши кількість варіантів закуски (3) на кількість варіантів для основної страви (5). Узагальнюємо цю методику як основне правило підрахунку:
Якщо нас попросять вибрати по одному елементу з кожної з двох окремих категорій, де є\(m\) товари в першій категорії і\(n\) елементи в другій категорії, то загальна кількість доступних варіантів буде\(m \cdot n\).
Це іноді називають правилом множення ймовірностей.
У списку читання для курсу англійської мови в коледжі є 21 роман і 18 томів поезії. Скільки різних способів студент може вибрати один роман і один том віршів для читання протягом кварталу?
Рішення
Є\(21\) вибір з першої категорії і\(18\) для другої, тому є\(21 \cdot 18 = 378\) можливості.
Основне правило підрахунку можна розширити, коли існує більше двох категорій, застосовуючи його повторно, як ми бачимо в наступному прикладі.
Припустимо, у певному ресторані у вас є три варіанти закуски (суп, салат або хлібні палички), п'ять варіантів для основної страви (гамбургер, бутерброд, кіш, фахіта або паста) та два варіанти десерту (пиріг або морозиво). Якщо вам дозволено вибрати саме один пункт з кожної категорії для вашої їжі, скільки різних варіантів їжі у вас є?
Рішення
Є\(3\) вибір для закуски,\(5\) для основної страви і\(2\) на десерт, тому є\(3 \cdot 5 \cdot 2 = 30\) можливості.
Вікторина складається з 3 правдивих чи неправдивих питань. Скільки способів студент може відповісти на вікторину?
Рішення
Є\(3\) питання. Кожне питання має\(2\) можливі відповіді (правдиві чи помилкові), тому на вікторину можна відповісти\(2 \cdot 2 \cdot 2 = 8\) по-різному. Нагадаємо, що ще один спосіб написання\(2 \cdot 2 \cdot 2\) - це\(2^3\), який набагато компактніше.
Припустимо, у певному ресторані у вас є вісім варіантів закуски, одинадцять варіантів для основної страви та п'ять варіантів десерту. Якщо вам дозволено вибрати саме один пункт з кожної категорії для вашої їжі, скільки різних варіантів їжі у вас є?
Перестановки
У цьому розділі ми розробимо ще більш швидкий спосіб вирішення деяких проблем, які ми вже навчилися вирішувати іншими способами. Почнемо з пари прикладів.
Скільки різних способів можна переставити букви слова MATH, щоб утворити кодове слово з чотирьох букв?
Рішення
Ця проблема трохи інша. Замість того, щоб вибрати один елемент з кожної з декількох різних категорій, ми неодноразово вибираємо елементи з однієї категорії (категорія: літери слова MATH) і кожен раз, коли ми вибираємо елемент, ми не замінюємо його, тому на наступному етапі є один вибір менше: у нас є 4 варіанти для першої літери (скажімо, ми вибираємо A), потім 3 варіанти для другої (M, T і H; скажімо, ми вибираємо H), потім 2 варіанти для наступної літери (M і T; скажімо, ми вибираємо M) і тільки один вибір на останньому етапі (T). Таким чином, є\(4 \cdot 3 \cdot 2 \cdot 1 = 24\) способи написання коду варто з літерами MATH.
У цьому прикладі нам потрібно було провести розрахунок\(n \cdot (n – 1) \cdot (n – 2) ··· 3 \cdot 2 \cdot 1\). Цей розрахунок часто з'являється в математиці, і називається факторіал, і позначається\(n!\)
Факторіал, коли ми беремо натуральне число і знаходимо добуток всіх спадних натуральних чисел, включаючи себе, аж до 1:
\[n! = n \cdot (n – 1) \cdot (n – 2) ··· 3 \cdot 2 \cdot 1 \nonumber \]
Ми говоримо\(n!\) як «\(n\)факторіал». Наприклад, дано 5! , то ми говоримо «5 факторіал».
Скільки способів п'ять різних дверних призів можуть бути розподілені між п'ятьма людьми?
Рішення
Є 5 варіантів призу для першої особи, 4 варіанти для другої і так далі. Кількість способів розподілу призів буде\(5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\) способами.
Зараз ми розглянемо кілька дещо інших прикладів.
Благодійну допомогу беруть участь 25 осіб, а в якості дверних призів видаються три подарункові сертифікати: один подарунковий сертифікат в розмірі 100 доларів, другий коштує 25 доларів, а третій коштує 10 доларів. Якщо припустити, що жодна людина не отримує більше одного призу, скільки різних способів можна вручити три подарункові сертифікати?
Рішення
Використовуючи Основне правило підрахунку, існує 25 варіантів для особи, яка отримує сертифікат $100, 24 решти варіантів для сертифіката $25 і 23 варіанти для сертифіката $10, тому є\(25 \cdot 24 \cdot 23 = 13,800\) способи, за допомогою яких призи можуть бути присуджені.
Вісім спринтерів вийшли до олімпійського фіналу в 100-метровій гонці. Скільки різних способів можуть бути нагороджені золоті, срібні та бронзові медалі?
Рішення
Використовуючи Основне правило підрахунку, є 8 варіантів для переможця золотої медалі, 7 решти варіантів для срібла та 6 для бронзи, тому є\(8 \cdot 7 \cdot 6 = 336\) способи, як три медалі можуть бути нагороджені 8 бігунів.
Зверніть увагу, що в цих попередніх прикладах подарункові сертифікати та олімпійські медалі були нагороджені без заміни; тобто, як тільки ми вибрали переможця призу за перші двері або золотої медалі, вони не мають права на інші призи. Таким чином, на кожному наступному етапі рішення залишається на один вибір менше (25, потім 24, потім 23 в першому прикладі; 8, потім 7, потім 6 у другому). Протипоставте це з ситуацією тесту з декількома варіантами вибору, де може бути п'ять можливих відповідей - A, B, C, D або E - для кожного питання тесту.
Зауважте також, що порядок вибору був важливим у кожному прикладі: для трьох дверних призів, обраний першим означає, що ви отримуєте значно більше грошей; в прикладі Олімпіади перший означає, що ви отримаєте золоту медаль замість срібла або бронзи. У кожному випадку, якби ми обрали однакових трьох людей в іншому порядку, могла бути інша людина, яка отримала приз у розмірі 100 доларів, або інший золотий призер. (На відміну від ситуації, коли ми можемо витягнути три імена з капелюха, щоб кожен отримав подарунковий сертифікат на 10 доларів; в цьому випадку порядок вибору не важливий, оскільки кожен з трьох людей отримує однаковий приз. Ситуації, коли порядок не важливий, будуть розглянуті в наступному розділі.)
Ми можемо узагальнити ситуацію в двох прикладах вище до будь-якої проблеми без заміни, де важливий порядок вибору. Якщо ми організуємо в порядку r елементів з n можливостей (замість 3 з 25 або 3 з 8, як у попередніх прикладах), кількість можливих домовленостей буде вказано
\[n \cdot (n – 1) \cdot (n – 2) ··· (n – r + 1) \nonumber \]
Якщо ви не розумієте,\((n — r + 1)\) чому потрібне число для останнього фактора, просто подумайте про перший приклад у цьому розділі, де ми розраховували,\(25 \cdot 24 \cdot 23\) щоб отримати\(13,800\). У цьому випадку\(n = 25\) і\(r = 3\), значить\(n — r + 1 = 25 — 3 + 1 = 23\), яке саме правильне число для кінцевого коефіцієнта.
Тепер, чому ми хочемо використовувати цю складну формулу, коли насправді простіше використовувати Основне правило підрахунку, як ми робили в перших двох прикладах? Ну, ми насправді не будемо використовувати цю формулу все так часто, ми тільки розробили її так, щоб ми могли прикріпити спеціальне позначення і спеціальне визначення до цієї ситуації, коли ми вибираємо\(r\) елементи з\(n\) можливостей без заміни і де порядок вибору важливо.
\[_nP_r = n \cdot (n – 1) \cdot (n – 2) ··· (n – r + 1) \nonumber \]
Ми говоримо, що існують nPR перестановки розміру r, які можуть бути обрані з числа n варіантів без заміни, коли порядок має значення.
Виявляється, ми можемо висловити цей результат простіше за допомогою факторіалів.
\[_nP_r = \dfrac{n!}{(n-r)!} \nonumber \]
У практичності ми зазвичай використовуємо технологію, а не факторіали або повторне множення для обчислення перестановок.
У мене дев'ять картин, і у мене є місце, щоб відобразити лише чотири з них одночасно на моїй стіні. Скільки різних способів я міг це зробити?
Рішення
Оскільки ми вибираємо\(4\) картини з\(9\) без заміни, де важливий порядок вибору, є\(_9P_4 = 9 \cdot 8 \cdot 7 \cdot 6 = 3,024\) перестановки.
Скільки способів може бути обраний виконавчий комітет з чотирьох осіб (президент, віце-президент, секретар, скарбник) з ради директорів неприбуткової організації з 16 членів?
Рішення
Ми хочемо вибрати\(4\) людей з\(16\) без заміни і там, де важливий порядок підбору. Отже, відповідь є\(_16P_4 = 16 \cdot 15 \cdot 14 \cdot 13 = 43,680\).
Скільки 5-ти символьних паролів можна зробити за допомогою букв від А до Я
a. якщо дозволено повторення
б. якщо не допускаються повторення
Комбінації
У попередньому розділі ми розглянули ситуацію, коли вибирали\(r\) елементи з\(n\) можливостей без заміни і де був важливий порядок підбору. Ми зараз розглянемо подібну ситуацію, при якій порядок підбору не важливий.
Благодійну допомогу беруть участь 25 осіб, на яких три подарункові сертифікати $50 видаються як дверні призи. Припускаючи, що жодна людина не отримує більше одного призу, скільки різних способів можна вручити подарункові сертифікати?
Рішення
Використовуючи Основне правило підрахунку, існує 25 варіантів для першої особи, 24 решти варіантів для другої особи і 23 для третьої, тому є\(25 \cdot 24 \cdot 23 = 13,800\) способи вибрати трьох людей. Припустимо на мить, що Абе вибирають першим, Беа другий і Сінді третій; це один з 13 800 можливих результатів. Іншим способом присудження призів було б вибрати Абе першого, Сінді другого і Беа третього; це ще один з\(13,800\) можливих результатів. Але в будь-якому випадку Абе, Беа, і Сінді кожен отримують $50, так що насправді не має значення порядку, в якому ми їх вибираємо. У скільки різних замовлень можна вибрати Абе, Беа та Сінді? Виявляється, їх 6:
ABC ACB НАЗАД БКА КАБІНИ КАБІНИ
Як ми можемо бути впевнені, що порахували їх усіх? Ми дійсно просто вибираємо\(3\) людей з\(3\), тому є\(3 \cdot 2 \cdot 1 = 6\) способи зробити це; нам насправді не потрібно перераховувати їх усіх, ми можемо просто використовувати перестановки!
Отже, із\(13,800\) способів відбору\(3\) людей\(25\), шість із них включають Абе, Беа та Сінді. Цей же аргумент працює для будь-якої іншої групи з трьох людей (скажімо, Абе, Беа та Девід або Френк, Глорія та Хілді), тому кожна група з трьох осіб зараховується шість разів. Таким чином,\(13,800\) цифра в шість разів занадто велика. Кількість окремих груп з трьох осіб буде\(\dfrac{13,800}{6} = 2300\).
Ми можемо узагальнити ситуацію в цьому прикладі вище до будь-якої проблеми вибору колекції предметів без заміни, де порядок вибору не важливий. Якщо ми вибираємо\(r\) елементи поза\(n\) можливостями (замість 3 з 25, як у попередніх прикладах), кількість можливих варіантів буде дано\(\dfrac{_nP_r}{_rP_r}\), і ми могли б використовувати цю формулу для обчислень. Однак така ситуація виникає настільки часто, що ми додаємо спеціальне позначення та спеціальне визначення до цієї ситуації, коли ми вибираємо\(r\) предмети з\(n\) можливостей без заміни, де порядок вибору не важливий.
\[_nC_r = \dfrac{_nP_r}{_rP_r} \nonumber \]
Ми говоримо, що існують\(_nC_r\) комбінації розміру\(r\), які можуть бути обрані з числа\(n\) варіантів без заміни, де порядок не має значення. Ми також можемо записати формулу комбінацій через факторіали:
\[_nC_r = \dfrac{n!}{(n-r)!r!} \nonumber \]
Група з чотирьох студентів повинна бути обрана з класу 35 членів для представлення класу в студентській раді. Скільки способів це можна зробити?
Рішення
Оскільки ми вибираємо 4 людини з 35 без заміни, де порядок підбору не важливий, є\(_{35}C_4 = \dfrac{35 \cdot 34 \cdot 33 \cdot 32}{4 \cdot 3 \cdot 2 \cdot 1} = 52,360\) комбінації.
Комітет з асигнувань Сенату Сполучених Штатів складається з 29 членів; Підкомітет з питань оборони Комітету з асигнувань складається з 19 членів. Не враховуючи партійну приналежність чи будь-які спеціальні місця у Підкомітеті, скільки різних підкомітетів 19 членів можуть бути обрані з числа 29 Сенаторів Комітету з асигнувань?
У попередній проблемі Try it Now ми припустили, що 19 членів Підкомітету оборони були обрані без урахування партійної приналежності. Насправді цього ніколи не станеться: якщо республіканці перебувають у більшості, вони ніколи не дозволять більшості демократів сидіти (і, таким чином, контролювати) будь-який підкомітет. (Те саме, звичайно, було б правдою, якби демократи контролювали.) Отже, розглянемо приклад ще раз, в трохи більш складному вигляді.
Комітет з асигнувань Сенату Сполучених Штатів складається з 29 членів, 15 республіканців і 14 демократів. Підкомітет оборони складається з 19 членів, 10 республіканців і 9 демократів. Скільки різних способів можна обрати членів Підкомітету з питань оборони з числа 29 сенаторів у Комітеті з асигнувань?
Рішення
У цьому випадку нам потрібно вибрати 10 з 15 республіканців і 9 з 14 демократів. Є\(_{15}C_{10} = 3003\) способи вибрати 10 республіканців і\(_{14}C_{9} = 2002\) способи вибрати 9 демократів. Але що тепер? Як ми закінчимо проблему?
Припустимо, ми перерахували всі можливі 10-членні республіканські групи на 3003 промахи червоного паперу та всі можливі 9-членські демократичні групи на 2002 промахи синього паперу. Скільки способів ми можемо вибрати один червоний ковзання та один синій ковзання? Це робота для Основного правила підрахунку! Ми просто робимо один вибір з першої категорії і один вибір з другої категорії, як і в питаннях меню ресторану з раніше.
Повинні бути\(3003 \cdot 2002 = 6,012,006\) можливі шляхи відбору членів Оборонного підкомітету.
Імовірність використання перестановок і комбінацій
Ми можемо використовувати перестановки та комбінації, щоб допомогти нам відповісти на більш складні питання ймовірності
Вибрано 4-значний PIN-код. Яка ймовірність того, що повторюваних цифр немає?
Рішення
Існує 10 можливих значень для кожної цифри PIN-коду (а саме: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), тому є\(10 \cdot 10 \cdot 10 \cdot 10 = 104 = 10,000\) загальні можливі номери PIN-кодів.
Щоб не було повторюваних цифр, всі чотири цифри повинні бути різними, що вибирається без заміни. Ми могли б або обчислити\(10 \cdot 9 \cdot 8 \cdot 7\), або помітити, що це те ж саме, що і перестановка\(_{10}P_4 = 5040\).
Імовірність відсутності повторюваних цифр - це кількість 4-значних PIN-номерів без повторюваних цифр, поділених на загальну кількість 4-значних PIN-номерів. Така ймовірність
\(\dfrac{_{10}P_4}{10^4} = \dfrac{5040}{10000} = 0.504\)
Отже, існує 50,4% ймовірність того, що 4-значний PIN-код не має повторюваних цифр.
У лотереї певного штату 48 куль під номером від 1 до 48 поміщаються в машину і шість з них витягуються випадковим чином. Якщо шість намальованих чисел збігаються з числами, які гравець вибрав, гравець виграє 1 000 000 доларів. У цій лотереї порядок малювання номерів не має значення. Обчисліть ймовірність того, що ви виграєте приз на мільйон доларів, якщо придбаєте один лотерейний квиток.
Рішення
Для того, щоб обчислити ймовірність, нам потрібно підрахувати загальну кількість способів, які можна намалювати шість чисел, і кількість способів шість чисел на квитку гравця можуть збігатися з шістьма числами, витягнутими з машини. Оскільки немає умови, що цифри будуть в якомусь певному порядку, кількість можливих результатів розіграшу лотереї є\(_{48}C_6 = 12,271,512\). З цих можливих результатів лише один збігається з усіма шістьма номерами на квитку гравця, тому ймовірність виграшу головного призу становить:
\(\dfrac{_{6}C_6}{_{48}C_6} = \dfrac{1}{12271512} ≈ 0.0000000815\)
Таким чином, є менше 1% шансів виграти головний приз.
У державній лотереї з попереднього прикладу, якщо п'ять з шести намальованих чисел відповідають числам, які гравець вибрав, гравець виграє другий приз у розмірі 1000 доларів. Обчисліть ймовірність того, що ви виграєте другий приз, якщо придбаєте один лотерейний квиток.
Рішення
Як зазначено вище, кількість можливих результатів розіграшу лотереї становить\(_{48}C_6 = 12,271,512\). Для того, щоб виграти другий приз, п'ять з шести номерів на квитку повинні відповідати п'яти з шести виграшних номерів; іншими словами, ми повинні були вибрати п'ять з шести виграшних номерів і один з 42 програшних номерів. Кількість способів вибрати 5 з 6 виграшних номерів дається\(_6C_5 = 6\) і кількість способів вибрати 1 з 42 програшних чисел дається\(_{42}C_1 = 42\). Таким чином, кількість сприятливих результатів потім задається Основним правилом підрахунку:\(_6C_5 \cdot _{42}C_1 = 6 \cdot 42 = 252\). Отже, ймовірність виграти другий приз є.
\(\dfrac{_{6}C_6}{_{48}C_6} = \dfrac{1}{12271512} ≈ 0.0000000815\)
Це означає, що є менше 1% шансів виграти другий приз. Ого! Тепер ми можемо зрозуміти, чому деякі люди називають це «удачею» при виграші в лотерею, оскільки шанси на виграш настільки низькі.
Питання з декількома варіантами на економічній вікторині містить 10 питань з п'ятьма можливими відповідями на кожне. Обчислити ймовірність випадковим чином вгадати відповіді і отримати 9 питань правильно.
Обчислити ймовірність випадкового витягування п'яти карт з колоди і отримання рівно одного туза.
Рішення
У багатьох карткових іграх (наприклад, покер) порядок, в якому карти витягуються, не важливий (оскільки гравець може переставити карти в руці будь-яким способом, який він вибере); у наступних проблемах ми будемо вважати, що це так, якщо не вказано інше. Таким чином, ми використовуємо комбінації для обчислення можливої кількості 5-карткових рук,\(_{52}C_5\). Це число буде йти в знаменник нашої формули ймовірності, так як це число можливих результатів.
Для чисельника нам знадобиться кількість способів витягнути з колоди один Туз і чотири інші карти (жодна з них тузи). Оскільки є чотири тузи, і ми хочемо саме один з них, будуть\(_4C_1\) способи вибрати одного туза; оскільки є 48 не-тузів, і ми хочемо 4 з них, буде 48C4 способів вибрати чотири не-тузи. Тепер ми використовуємо Основне правило підрахунку, щоб обчислити, що будуть\(_4C_1 \cdot _{48}C_4\) способи вибрати одного туза і чотирьох не-тузів.
Збираючи це все разом, ми маємо
\(P(\text{one Ace}) = \dfrac{(_{4}C_1)(_{48}C_4)}{(_{52}C_5)} = \dfrac{778320}{2598960} ≈ 0.299\)
Таким чином, існує приблизно 30% шанс намалювати рівно одного Туза в руку з 5 карт.
Обчислити ймовірність випадкового витягування п'яти карт з колоди і отримання рівно двох тузів.
Рішення
Рішення схоже на попередній приклад, за винятком того, що зараз ми вибираємо 2 тузи з 4 і 3 без тузів з 48; знаменник залишається тим самим:
\(P(\text{two Aces}) = \dfrac{(_{4}C_2)(_{48}C_3)}{(_{52}C_5)} = \dfrac{103776}{2598960} ≈ 0.0399\)
Існує близько 4% шансів витягнути 2 тузів в руку з 5 карт. Зверніть увагу з прикладу 37, ймовірність намалювання рівно одного туза набагато вище, ніж малювання два.
Обчислити ймовірність випадкового витягування п'яти карт з колоди карт і отримання трьох тузів і двох королів.
Проблема дня народження
Давайте зробимо паузу, щоб розглянути відому проблему в теорії ймовірностей:
Припустимо, у вас є кімната, заповнена 30 чоловік. Яка ймовірність того, що є хоча б один спільний день народження?
Візьміть припущення на відповідь на вищевказану проблему. Чи була ваша здогадка досить низькою, як близько 10%? Це, здається, інтуїтивна відповідь (\(\dfrac{30}{365}\)можливо?). Давайте подивимося, чи варто прислухатися до нашої інтуїції. Почнемо з більш простої проблеми, однак.
Припустимо, три людини знаходяться в кімнаті. Яка ймовірність того, що серед цих трьох людей є хоча б один спільний день народження?
Рішення
Є багато способів там може бути принаймні один спільний день народження. На щастя, є більш простий спосіб. Ми запитуємо себе: «Яка альтернатива хоча б одному спільному дню народження?» У цьому випадку альтернативою є те, що спільних днів народження немає. Іншими словами, альтернативи «принаймні одному» немає. Іншими словами, оскільки це взаємодоповнююча подія,
\(P(\text{at least one}) = 1 – P(\text{none})\)
Потім ми почнемо з обчислення ймовірності того, що спільного дня народження немає. Уявімо, що ви один з цих трьох людей. Ваш день народження може бути будь-яким без конфлікту, тому є 365 варіантів з 365 для вашого дня народження. Яка ймовірність того, що друга людина не розділить ваш день народження? Є 365 днів у році (давайте ігноруємо високосні роки) і видаляючи ваш день народження від суперечок, є 364 варіанти, які гарантують, що ви не поділяєте день народження з цією людиною, тому ймовірність того, що друга людина не поділить ваш день народження, є\(\dfrac{364}{365}\). Тепер переходимо до третьої особи. Яка ймовірність того, що у цієї третьої особи немає такого ж дня народження, як ні у вас, ні у другої людини? Є 363 дні, які не будуть дублювати ваш день народження або друга людина, тому ймовірність того, що третя людина не розділить день народження з першими двома є\(\dfrac{363}{365}\).
Ми хочемо, щоб друга людина не ділив з вами день народження, а третя людина не ділив день народження з першими двома людьми, тому використовуємо правило множення:
\(P(\text{no shared birthday}) = \dfrac{365}{365} \cdot \dfrac{364}{365} \cdot \dfrac{363}{365} ≈ 0.9918 \)
а потім відняти від 1, щоб отримати
\(P(\text{shared birthday}) = 1 – P(\text{no shared birthday}) = 1 – 0.9918 = 0.0082\)
Це означає, що менше 1% шансів, що людина в кімнаті з 3 має хоча б один спільний день народження.
Це досить невелика кількість, тому, можливо, має сенс, що відповідь на нашу первісну проблему буде невеликим. Давайте зробимо нашу групу трохи більшою.
Припустимо, п'ять чоловік знаходяться в кімнаті. Яка ймовірність того, що серед цих п'яти людей є хоча б один спільний день народження?
Рішення
Продовжуючи закономірність попереднього прикладу, відповідь повинна бути
\(P(\text{shared birthday}) = 1 – \dfrac{365}{365} \cdot \dfrac{364}{365} \cdot \dfrac{363}{365} \cdot \dfrac{362}{365} \cdot \dfrac{361}{365} ≈ 0.0271\)
Зверніть увагу, що ми могли б переписати це більш компактно, як
\(P(\text{shared birthday}) = 1 – \dfrac{_{365}P_5}{365^5} ≈ 0.0271\)
що робить його трохи простіше ввести в калькулятор або комп'ютер, і який пропонує хорошу формулу, оскільки ми продовжуємо розширювати населення нашої групи.
Припустимо, 30 осіб знаходяться в кімнаті. Яка ймовірність того, що серед цих 30 осіб є хоча б один спільний день народження?
Рішення
Тут ми можемо розрахувати
\(P(\text{shared birthday}) = 1 – \dfrac{_{365}P_{30}}{365^{30}} ≈ 0.706\)
що дає нам дивовижний результат, що коли ви перебуваєте в кімнаті з 30 людьми, є 70% шансів, що буде хоча б один спільний день народження.
Якщо ви любите робити ставки, і якщо ви можете переконати 30 людей розкрити свої дні народження, ви, можливо, зможете виграти гроші, зробивши ставку на одного, що в кімнаті буде принаймні дві людини з одним днем народження в будь-який час ви знаходитесь в кімнаті 30 або більше людей. (Звичайно, вам потрібно буде переконатися, що ваш друг не вивчив ймовірність!) Ви не гарантовано виграєте, але ви повинні виграти більше половини часу.
Це один з багатьох результатів теорії ймовірності, яка є контрінтуїтивною; тобто це суперечить нашим інстинктам кишечника. Якщо ви все ще не вірите математиці, ви можете провести моделювання. Просто так вам не доведеться йти навколо округлення груп з 30 осіб, хтось люб'язно розробив Java аплет, щоб ви могли провести комп'ютерне моделювання. Перейдіть на цю веб-сторінку: http://www-stat.stanford.edu/~susan/... /Birthday.html, і після завантаження аплету виберіть 30 днів народження, а потім продовжуйте натискати кнопку Пуск і Скинути. Якщо ви відстежуєте кількість разів, коли відбувається повторний день народження, ви повинні отримати повторний день народження приблизно 7 з кожних 10 разів, коли ви запускаєте симуляцію.
Припустимо, 10 осіб знаходяться в кімнаті. Яка ймовірність того, що серед цих 10 людей є хоча б один спільний день народження?
