11.6: Міри варіації
- Page ID
- 66140
Розглянемо ці три набори балів вікторини:
- Секція А: 5 5 5 5 5 5 5 5 5 5
- Секція Б: 0 0 0 0 10 10 10
- Секція С: 4 4 4 5 5 5 5 6 6 6
Всі три з цих наборів даних мають середнє значення 5 і медіану 5, але набори балів явно зовсім різні. У розділі А всі мали однаковий бал; у розділі B половина класу не отримала очок, а інша половина отримала ідеальний бал, припускаючи, що це була 10-бальна вікторина. Розділ C не був таким послідовним, як розділ A, але не настільки широко різноманітним, як розділ B.
На додаток до середнього та медіани, які є мірами «типового» або «середнього» значення, нам також потрібна міра того, наскільки «розкинутий» або різноманітний кожен набір даних.
Існує кілька способів вимірювання цього «поширення» даних. Перший є найпростішим і називається діапазоном.
Діапазон - це різниця між максимальним значенням і мінімальним значенням набору даних.
Використовуючи результати вікторини зверху,
Для розділу A діапазон дорівнює 0, оскільки максимальний і мінімальний рівні 5 і\(5 – 5 = 0\)
Для секції B діапазон дорівнює 10, оскільки\(10 – 0 = 10\)
Для секції С діапазон дорівнює 2, так як\(6 – 4 = 2\)
В останньому прикладі діапазон, здається, виявляє, наскільки поширені дані. Однак припустимо, що ми додамо четвертий розділ, розділ D, з оцінками 0 5 5 5 5 5 5 10.
Цей розділ також має середнє і медіану 5. Діапазон 10, але цей набір даних зовсім інший, ніж розділ B. Щоб краще висвітлити відмінності, нам доведеться звернутися до більш складних заходів зміни.
Стандартне відхилення - це міра варіації, заснована на вимірюванні того, наскільки кожне значення даних відхиляється або відрізняється від середнього. Кілька важливих характеристик:
- Стандартне відхилення завжди позитивне. Стандартне відхилення буде дорівнювати нулю, якщо всі значення даних рівні, і буде збільшуватися в міру поширення даних.
- Стандартне відхилення має ті ж одиниці, що і вихідні дані.
- Стандартне відхилення, як і середнє, може сильно впливати на викиди.
Використовуючи дані з розділу D, ми могли б обчислити для кожного значення даних різницю між значенням даних та середнім значенням:
\ (\ begin {масив} {|l|l|}
\ hline\ текст {значення даних} &\ текст {відхилення: значення даних - середнє}
\\ hline 0 & 0-5 = -5
\\ hline 5 & 5-5 = 0
\\ hline 5 & 5-5 = 0
\\\ hline 5 & 5-5 = 0
\\ hline 5 & 5-5
\ hline 5 & 5-5 = 0\\
\ hline 5 & 5-5 = 0\\
\ hline 5 & 5-5 = 0\\
\ hline 5 & 5-5 = 0\\
\ hline 10 & 10-5 = 5\\
\ hline
\ кінець {масив}\)
Ми хотіли б отримати уявлення про «середнє» відхилення від середнього, але якщо ми знайдемо середнє значення у другому стовпці, негативні та позитивні значення скасовують один одного (це буде завжди), тому, щоб запобігти цьому, ми квадратимо кожне значення у другому стовпці:
Потім ми додаємо квадратні відхилення вгору, щоб отримати\(25 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 25 = 50\). Зазвичай ми ділимо на кількість балів (у цьому випадку 10), щоб знайти середнє значення відхилень.\(n\) Але ми робимо це лише тоді, коли набір даних представляє сукупність; якщо набір даних представляє вибірку (як це майже завжди), ми замість цього ділимо на\(n - 1\) (у цьому випадку\(10 - 1 = 9\)). [1]
Таким чином, в нашому прикладі, ми б,\(\frac{50}{10} = 5\) якщо розділ D представляє сукупність і\(\frac{50}{9} =\) близько 5.56, якщо розділ D представляє зразок. Ці значення (5 і 5,56) називаються відповідно дисперсією популяції і дисперсією вибірки для розділу D.
Дисперсія може бути корисною статистичною концепцією, але зауважте, що одиниці дисперсії в цьому випадку будуть квадратними точками, оскільки ми звели всі відхилення в квадраті. Що таке точки-квадрат? Гарне запитання. Ми хотіли б мати справу з одиницями, з яких ми почали (точки в цьому випадку), тому для перетворення назад ми беремо квадратний корінь і отримуємо:
\[\text{population standard deviation} =\sqrt{\frac{50}{10}}=\sqrt{5} \approx 2.2 \nonumber \]
або
\[\text{sample standard deviation} =\sqrt{\frac{50}{9}} \approx 2.4 \nonumber \]
Якщо ми не впевнені, чи є набір даних вибіркою чи сукупністю, ми зазвичай вважаємо, що це зразок, і ми округляємо відповіді на ще один десятковий знак, ніж вихідні дані, як ми зробили вище.
- Знайдіть відхилення кожного з даних від середнього. Іншими словами, відніміть середнє значення від значення даних.
- Квадрат кожного відхилення.
- Складіть квадратні відхилення.
- Розділити на\(n\), кількість значень даних, якщо дані представляють цілу сукупність; розділити на,\(n – 1\) якщо дані з вибірки.
- Обчислити квадратний корінь результату.
Обчисливши стандартне відхилення для розділу В вище, ми спочатку обчислимо, що середнє значення дорівнює 5. Використання таблиці може допомогти відстежувати ваші обчислення для стандартного відхилення:
\ (\ begin {масив} {|l|l|}
\ hline\ текст {значення даних} &\ текст {відхилення: значення даних - середнє} &\ текст {відхилення у квадраті}\
\ hline 0 & 0-5 = -5 & (-5) ^ {2} =25\
\ hline 0 & 0-5 = -5 & (-5) ^ {2} =25\
\ hline 0 & 0-5 & (-5) ^ {2} 5 = -5 & (-5) ^ {2} =25\
\ hline 0 & 0-5 = -5 & (-5) ^ {2} =25\
\ hline 0 & 0-5 = -5 & (-5) ^ {2} =25
\\ hline 10 & 10-5=5 & (5) ^ {2} =25
\\ hline 10 і 10-5=5 & (5) ^ {2} =25\
\ hline 10 & 10-5=5 & (5) ^ {2} =25\\
\ hline 10 & 10-5 = 5 & (5) ^ {2} =25\
\ hline 10 & 10-5 = 5 & (5) ^ {2} =25\
\ hline
\ кінець {масив}\)
Припускаючи, що ці дані представляють сукупність, ми додамо квадратні відхилення, розділимо на 10, кількість значень даних і обчислимо квадратний корінь:
\[\sqrt{\frac{25+25+25+25+25+25+25+25+25+25}{10}}=\sqrt{\frac{250}{10}}=5 \nonumber \]
Зверніть увагу, що стандартне відхилення цього набору даних набагато більше, ніж у розділі D, оскільки дані в цьому наборі більш поширені.
Для порівняння стандартними відхиленнями всіх чотирьох перетинів є:
\ (\ почати {масив} {|l|l|}
\ hline\ текст {Розділ A: 5 5 5 5 5 5 5} &\ текст {Стандартне відхилення: 0}
\\ hline\ текст {Розділ B: 0 0 0 0 10 10 10 10} &\ текст {Стандартне відхилення: 5}
\\ hline\ текст {Розділ C: 4 4 5 5 5 6 6} &\ текст { Стандартне відхилення: 0,8}\
\ hline\ текст {Розділ D: 0 5 5 5 5 5 5 5 5 10} &\ текст {Стандартне відхилення: 2.2}\
\ hline
\ end {масив}\)
Ціна банки арахісового масла в 5 магазинах становила: $3,29, $3,59, $3,79, $3,75 і $3,99. Знайдіть стандартне відхилення цін.
- Відповідь
-
Раніше ми виявили, що середнє значення даних становило $3.682.
\ (\ begin {масив} {|l|l|}
\ hline\ текст {значення даних} &\ текст {відхилення: значення даних - середнє} &\ текст {відхилення у квадраті}\
\ hline 3.29 & 3.29-3.682 = -0.391 & 0.153664\
\ hline 3.59 & 3.59-3.682 = -0.092 & 0.008464\\\
\ hline 3.79 & 3.79-3.682 = 0.108 & 0.011664\
\ hline 3.75 & 3.75-3.682 = 0.068 & 0.004624\
\ hline 3.99 & 3.99-3.682 = 0,308 & 0.094864\\
\ hline
\ кінець {масив}\)Ці дані взяті з вибірки, тому ми додамо квадратні відхилення, розділимо на 4, кількість значень даних мінус 1, і обчислимо квадратний корінь:
\(\sqrt{\frac{0.153664+0.008464+0.011664+0.004624+0.094864}{4}} \approx \$ 0.261\)
Де стандартне відхилення - це міра варіації, заснована на середньому, квартилі базуються на медіані.
Квартили - це значення, які ділять дані на квартали.
Перший квартиль (\(Q_1\)) - це значення таким чином, щоб 25% значень даних знаходилися нижче нього; третій квартиль (\(Q_3\)) - це значення так, що 75% значень даних знаходяться нижче нього. Можливо, ви здогадалися, що другий квартиль такий же, як і медіана, оскільки медіана - це значення, так що 50% значень даних знаходяться нижче неї.
Це ділить дані на чверті; 25% даних знаходиться між мінімальним і\(Q_1\), 25% - між\(Q_1\) і медіаною, 25% - між медіаною і\(Q_3\), і 25% - між\(Q_3\) і максимальним значенням
Хоча квартилі не є 1-числовим підсумком варіації, як стандартне відхилення, квартилі використовуються з медіаною, мінімальними та максимальними значеннями для формування зведення даних з 5 чисел.
Резюме з п'яти чисел набуває такого вигляду:
Мінімальний,\(Q_1\), Медіана\(Q_3\), Максимум
Щоб знайти перший квартиль, нам потрібно знайти значення даних так, щоб 25% даних знаходилося нижче нього. Якщо\(n\) кількість значень даних, ми обчислюємо локатор, знаходячи 25% від\(n\). Якщо цей локатор є десятковим значенням, ми округляємо і знаходимо значення даних в цій позиції. Якщо локатор є цілим числом, ми знаходимо середнє значення даних у цій позиції та наступне значення даних. Це ідентично процесу, який ми використовували для пошуку медіани, за винятком того, що ми використовуємо 25% значень даних, а не половину значень даних як локатор.
Почніть з упорядкування даних від найменшого до найбільшого
Обчислити локатор:\(L = 0.25n\)
Якщо\(L\) десяткове значення:
Округлити до\(L+\)
Використовуйте значення даних у\(L+^{\text{th}}\) позиції
Якщо\(L\) ціле число:
Знайдіть середнє значення значень даних в\(L+1^{\text{th}}\) позиціях\(L^{\text{th}}\) і.
Скористайтеся тією ж процедурою, що\(Q_1\) і для, але з локатором:\(L = 0.75n\)
Приклади повинні допомогти зробити це зрозуміліше.
Припустимо, ми виміряли 9 самок і їх висоти (в дюймах), відсортовані від найменшого до найбільшого:
59 60 62 64 66 67 69 70 72
Щоб знайти перший квартиль, ми спочатку обчислюємо локатор: 25% з 9 становить\(L = 0.25(9) = 2.25\). Так як це значення не є цілим числом, округляємо до 3. Перший квартиль буде третім значенням даних: 62 дюйма.
Щоб знайти третій квартиль, знову обчислюємо локатор: 75% з 9 - це\(0.75(9) = 6.75\). Так як це значення не є цілим числом, округляємо до 7. Третій квартиль буде сьомим значенням даних: 69 дюймів.
Припустимо, ми виміряли 8 самок і їх висоти (в дюймах), відсортовані від найменшого до найбільшого:
59 60 62 64 66 67 69 70
Щоб знайти перший квартиль, ми спочатку обчислюємо локатор: 25% з 8 становить\(L = 0.25(8) = 2\). Так як це значення є цілим числом, то знайдемо середнє значення 2-го і 3-го значень даних: (60+62) /2 = 61, тому перший квартиль дорівнює 61 дюйм.
Третій квартиль обчислюється аналогічно, використовуючи 75% замість 25%. \(L = 0.75(8) = 6\). Це ціле число, тому ми знайдемо середнє значення 6-го і 7-го значень даних:\(\frac{67+69}{2} = 68\),\(Q_3\) так і 68.
Зверніть увагу, що медіану можна обчислити так само, використовуючи 50%.
Підсумок з 5 чисел поєднує перший і третій квартиль з мінімальним, медіанним і максимальним значеннями.
Для 9 жіночої вибірки медіана - 66, мінімальна - 59, а максимальна - 72. Короткий зміст номера 5:59, 62, 66, 69, 72.
Для 8 жіночої вибірки медіана дорівнює 65, мінімальна - 59, а максимальна - 70, тому резюме 5 числа буде: 59, 61, 65, 68, 70.
Повертаючись до наших даних вікторини. У кожному випадку першим квартилем є локатор\(0.25(10) = 2.5\), тому перший квартиль буде 3-м значенням даних, а третій квартиль буде 8-м значенням даних. Створення резюме з п'яти чисел:
\ (\ begin {масив} {|l|l|}
\ hline\ текст {Розділ і дані} &\ текст {5-кількість резюме}\\ hline\ текст {Розділ A: 5 5 5 5 5 5 5} & 5,5,5,5,5,5\
\ hline\ текст {Розділ B: 0 0 0 0 0 10 10 10 10} & 0,0,5,10,10\\
\ hline\ текст {
Розділ C: 4 4 4 5 5 5 5 6 6} & 4,4,5,6,6\
\ hline\ текст {Розділ D: 0 5 5 5 5 5 5 5 5 10} & 0,5,5,10\\
\ hline
\ кінець {масив}\)
Звичайно, при відносно невеликому наборі даних знайти резюме з п'яти чисел трохи нерозумно, оскільки резюме містить майже стільки ж значень, скільки вихідних даних.
Загальна вартість підручників за семестр була зібрана з 36 студентів. Знайдіть зведення з числа 5 цих даних.
$140 $160 $160 $165 $180 $220 $235 $240 $250 $260 $280 $285
$285 $285 $290 $300 $305 $310 $310 $315 $320
$330 340 $345 $350 $355 $360 $360 $380 $395 $420 $460
- Відповідь
-
Дані вже в порядку, тому нам не потрібно спочатку їх сортувати.
Мінімальне значення - 140 доларів, а максимальне - 460 доларів.
Є 36 значень даних так,\(n=36 . n / 2=18,\) що є цілим числом, тому медіана - це середнє значення\(18^{\text {th }}\) і\(19^{\text {th }}\) даних,\(\$ 305\) і\(\$ 310\). Медіана -\(\$ 307.50\)
Щоб знайти перший квартиль, обчислюємо локатор,\(L=0.25(36)=9 .\) так як це ціле число, ми знаємо\(\mathrm{Q}_{1}\) середнє значення\(9^{\text {th }}\) і\(10^{\text {th }}\) даних,\(\$ 250\) і\(\$ 260 . \mathrm{Q}_{1}=\)\(\$ 255\)
Щоб знайти третій квартиль, обчислюємо локатор,\(L=0.75(36)=27 .\) так як це ціле число, ми знаємо\(Q_{3}\) середнє значення\(27^{\text {th }}\) і\(28^{\text {th }}\) даних,\(\$ 345\) і\(\$ 350\).
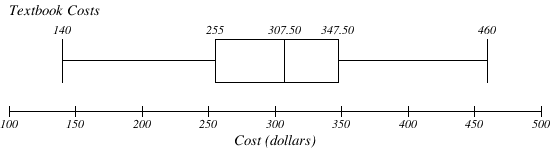
\(\mathrm{Q}_{3}=\$ 347.50\)Підсумок 5 цих даних: $140, $255, $307,50, $347,50, $460
Повертаючись до даних про доходи домогосподарств з більш ранніх, створіть резюме з п'яти чисел.
\ (\ почати {масив} {|l|l|}
\ hline\ textbf {Дохід (тисячі доларів)} &\ textbf {Частота}
\\ hline 15 & 6
\\ hline 20 & 8\
\\ hline 25 & 11\\
\ hline 30 & 17\\
\ hline 35 & 19\\
\ hline 40 & 20\\
\ hline 45 & 12\\
\ hline 50 & 7\\
\ hline\
\ кінець {масив}\)
Рішення
Додавши частоти, ми можемо побачити, що в таблиці представлені 100 значень даних. У прикладі 20 ми виявили, що медіана становила $35 тис. Ми бачимо в таблиці, що мінімальний дохід становить 15 тис. Доларів, а максимальний - $50 тис.
Щоб знайти\(Q_1\), обчислюємо локатор: L = 0,25 (100) = 25. Це ціле число, так\(Q_1\) буде середнє значення 25-го і 26-го значень даних.
Підрахувавши в даних, як ми робили раніше,
\(\begin{array}{ll} \text{There are 6 data values of \$15, so} & \text{Values 1 to 6 are \$15 thousand} \\ \text{The next 8 data values are \$20, so} & \text{Values 7 to (6+8)=14 are \$20 thousand} \\ \text{The next 11 data values are \$25, so} & \text{Values 15 to (14+11)=25 are \$25 thousand} \\ \text{The next 17 data values are \$30, so} & \text{Values 26 to (25+17)=42 are \$30 thousand} \end{array}\)
25-е значення даних становить $25 тис., А 26-е значення даних - $30 тис., Таким\(Q_1\) буде середнє значення цих:\((25 + 30)/2 = \$27.5\) тис.
Щоб знайти\(Q_3\), обчислюємо локатор:\(L = 0.75(100) = 75\). Це ціле число, так\(Q_3\) буде середнє значення 75-го і 76-го значень даних. Продовжуючи наш відлік від раніше,
\(\begin{array}{ll} \text{The next 19 data values are $35, so} & \text{Values 43 to (42+19)=61 are \$35 thousand} \\ \text{The next 20 data values are \$40, so} & \text{Values 61 to (61+20)=81 are \$40 thousand} \end{array}\)
І 75-е, і 76-е значення даних лежать в цій групі, так\(Q_3\) буде $40 тис.
Склавши ці значення воєдино в п'ятизначне резюме, отримаємо: 15, 27,5, 35, 40, 50
Зверніть увагу, що зведення числа 5 ділить дані на чотири інтервали, кожен з яких буде містити близько 25% даних. У попередньому прикладі це означає, що близько 25% домогосподарств мають дохід від 40 тисяч до 50 тисяч доларів.
Для візуалізації даних існує графічне зображення 5-числового резюме, яке називається графіком коробки, або графом коробки та вусів.
Коробковий сюжет - це графічне зображення резюме з п'яти чисел.
Для створення графіка коробки спочатку проводиться числова лінія. Від першої квартилі до третього квартилі проводиться коробка, а через коробку проводиться лінія на медіані. «Вуса» витягуються до мінімальних і максимальних значень.
Графік коробки нижче заснований на даних 9 жіночого зросту з резюме 5 номерів:
59, 62, 66, 69, 72.
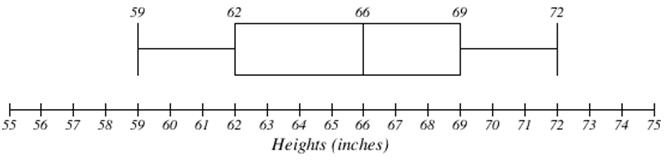
Графік коробки нижче заснований на даних про доходи домогосподарств із підсумком числа 5:
15, 27.5, 35, 40, 50
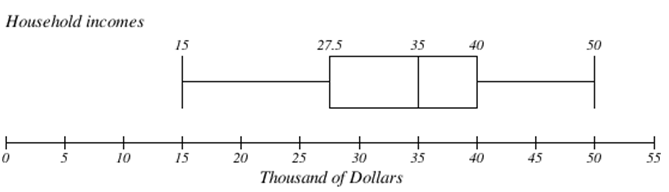
Створіть boxplot на основі даних про ціну підручника з останнього Спробуйте зараз.
- Відповідь
-
Коробкові ділянки особливо корисні для порівняння даних двох популяцій.
Графік часу обслуговування для двох ресторанів швидкого харчування показаний нижче.
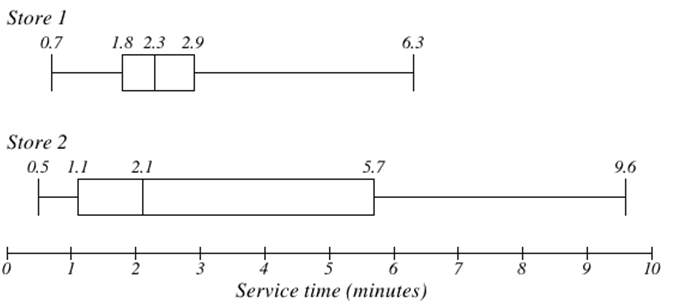
Хоча магазин 2 мав трохи коротший медіанний час обслуговування (2,1 хвилини проти 2.3 хвилини), магазин 2 менш послідовний, з більш широким розповсюдженням даних.
У магазині 1 75% клієнтів обслуговували протягом 2,9 хвилин, а в магазині 2 75% клієнтів обслуговували протягом 5,7 хвилин.
В який магазин варто піти поспіхом? Це залежить від вашої думки про удачу - 25% клієнтів у магазині 2 довелося чекати від 5.7 до 9.6 хвилин.
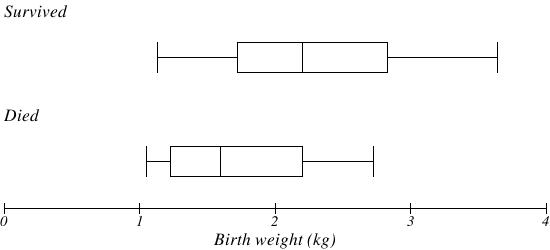
Наведений нижче графік заснований на вагах народження немовлят з важким ідіопатичним респіраторним дистрес-синдромом (SIRDS) [2]. Ділянка коробки відокремлена, щоб показати ваги народження немовлят, які вижили, і тих, хто цього не зробив.
Порівнюючи дві групи, бокссюжет показує, що вага народження немовлят, які померли, здається, в цілому менше, ніж вага немовлят, які вижили. Насправді ми бачимо, що середня вага при народженні немовлят, які вижили, така ж, як і третій квартиль немовлят, які померли.
Так само ми можемо бачити, що перший квартиль тих, хто вижив, більший за серединну вагу тих, хто загинув, тобто понад 75% тих, хто вижив, мали вагу при народженні більше, ніж середня вага при народженні тих, хто помер.
Дивлячись на максимальне значення для тих, хто загинув, і третій квартиль тих, хто вижив, ми можемо побачити, що понад 25% тих, хто вижив, мали вагу при народженні вище, ніж найважча немовля, яка померла.
Сюжет коробки дає нам швидкий, хоча і неформальний, спосіб визначити, що вага при народженні, швидше за все, пов'язана з виживанням немовлят з SIRDS.
[1] Причина, по якій ми робимо це, є високотехнічною, але ми можемо побачити, наскільки це може бути корисним, розглянувши випадок невеликої вибірки з популяції, яка містить викиди, що збільшить середнє відхилення: викид, швидше за все, не буде включений до вибірки, тому середнє відхилення вибірки буде недооцінюємо середнє відхилення населення; таким чином ми ділимо на трохи меншу кількість, щоб отримати трохи більше середнє відхилення.
[2] ван Vliet, P.K. і Гупта, J.M. (1973) Бікарбонат натрію при ідіопатичному респіраторному дистрес-синдромі. Арка. Хвороба в дитячому віці, 48, 249—255. Як цитується на http://openlearn.open.ac.uk/mod/ouco... §іон=1.1.3
