Skip to main content
LibreTexts - Ukrayinska

7.5: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    66478

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Навички

    1. Створіть диграф для наступного набору завдань:

    \ (\ begin {масив} {|l|l|}
    \ hline\ text {Завдання} &\ текст {Час потрібно} &\ begin {масив} {l}
    \ text {Завдання, які повинні бути}
    \\ текст {завершено першим}
    \ кінець {масив}
    \\ hline\ mathrm {A} & 3 &\
    \ hline\ mathrm {B } & 4 &\\
    \ hline\ mathrm {C} & 7 &
    \\\ hline\ mathrm {D} & 6 &\\ mathrm {A},
    \ mathrm {B}\\\ hline\ mathrm {E} & 5 &
    \ mathrm {B}\\ hline\ mathrm {D},\ mathrm {E}
    \\\ лінія\ математики {G} & підсилювач; 4 &\ mathrm {E}
    \\ лінія
    \ кінець {масив}\)

    1. Створіть диграф для наступного набору завдань:

    \ (\ begin {масив} {|l|l|}
    \ hline\ text {Завдання} &\ текст {Час потрібно} &\ begin {масив} {l}
    \ text {Завдання, які повинні бути}
    \\ текст {завершено першим}
    \ кінець {масив}
    \\ hline\ mathrm {A} & 3 &\
    \ hline\ mathrm {B } & 4 &\\
    \ hline\ mathrm {C} & 7 &
    \\\ hline\ mathrm {D} & 6 &\\
    mathrm {A}\\ hline\ mathrm {E} & 5 &\
    \ mathrm {A}\\ hline\ mathrm {F} & 5 &\
    \ mathrm {G} & 4 &\ mathrm {D},\ mathrm {E}\
    \ рядок
    \ кінець {масив}\)

    Використовуйте цей диграф для наступних 2 завдань.

    sc17.svg

    1. Використовуючи список пріоритетів\(\mathrm{T}_{4}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{3}, \mathrm{T}_{6}, \mathrm{T}_{2}, \mathrm{T}_{5}\), плануйте проект з двома процесорами.
    2. Використовуючи список пріоритетів\(\mathrm{T}_{5}, \mathrm{T}_{2}, \mathrm{T}_{3}, \mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4}, \mathrm{T}_{6}\), плануйте проект з двома процесорами.

    Використовуйте цей диграф для наступних 4 завдань.

    sc18.svg

    1. За допомогою списку пріоритетів\(\mathrm{T}_{4}, \mathrm{T}_{3}, \mathrm{T}_{9}, \mathrm{T}_{10}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{2}\) плануйте проект з двома процесорами.
    2. За допомогою списку пріоритетів\(\mathrm{T}_{2}, \mathrm{T}_{4}, \mathrm{T}_{6}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{9}\) плануйте проект з двома процесорами.
    3. За допомогою списку пріоритетів\(\mathrm{T}_{4}, \mathrm{T}_{3}, \mathrm{T}_{9}, \mathrm{T}_{10}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{2}\) плануйте проект з трьома процесорами.
    4. За допомогою списку пріоритетів\(\mathrm{T}_{2}, \mathrm{T}_{4}, \mathrm{T}_{6}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{9}\) плануйте проект з трьома процесорами.
    1. Скористайтеся алгоритмом зменшення часу, щоб створити список пріоритетів для диграфа з #3 та запланувати з двома процесорами.
    1. Скористайтеся алгоритмом зменшення часу, щоб створити список пріоритетів для диграфа з #3 та запланувати з трьома процесорами.
    1. Скористайтеся алгоритмом зменшення часу, щоб створити список пріоритетів для диграфа з #5 та запланувати з двома процесорами.
    1. Скористайтеся алгоритмом зменшення часу, щоб створити список пріоритетів для диграфа з #5 та запланувати з трьома процесорами.
    1. Використовуйте алгоритм зменшення часу, щоб створити список пріоритетів для проблеми з #1 та запланувати з двома процесорами.
    1. Використовуйте алгоритм зменшення часу, щоб створити список пріоритетів для проблеми з #2 та запланувати з двома процесорами.
    1. З диграфом від #3:

    а) Застосуйте алгоритм зворотного потоку, щоб знайти критичний час для кожного завдання

    b. знайти критичний шлях для проекту і мінімальний час завершення

    c Використовуйте алгоритм критичного шляху для створення списку пріоритетів та розкладу на двох процесорах.

    1. За допомогою digraph від #3 використовуйте алгоритм критичного шляху для планування на трьох процесорах.
    1. З диграфом від #5:

    а) Застосуйте алгоритм зворотного потоку, щоб знайти критичний час для кожного завдання

    b. знайти критичний шлях для проекту і мінімальний час завершення

    c Використовуйте алгоритм критичного шляху для створення списку пріоритетів та розкладу на двох процесорах.

    1. За допомогою digraph від #5 використовуйте алгоритм критичного шляху для планування на трьох процесорах.
    1. Використовуйте алгоритм критичного шляху, щоб запланувати проблему з #1 на двох процесорах.
    1. Використовуйте алгоритм критичного шляху, щоб запланувати проблему з #2 на двох процесорах.

    Концепції

    1. Якщо до диграфа додається додаткова вимога замовлення, чи може оптимальний час обробки коли-небудь стати довшим? Чи може оптимальний час обробки коли-небудь стати коротшим?
    1. Чи завжди оптимальний графік не матиме простоїв?
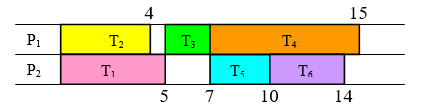
    1. Розглянемо диграф нижче.

    sc19.svg

    1. Скільки списків пріоритетів можна створити для цих завдань?
    2. Скільки унікальних графіків створено цими списками пріоритетів?
    1. Створіть диграф і список пріоритетів, які б привели до розкладу нижче.

    clipboard_ef0cf2d2798287b75ab51f13c0cd0dd90.png

    1. Чи можна створити диграф з трьома завданнями, для яких кожен можливий список пріоритетів створює різний графік? Якщо так, створіть його.
    1. Чи можна створити диграф з чотирма завданнями, для яких кожен можливий список пріоритетів створює різний графік? Якщо так, створіть його.

    Розвідка

    1. Самостійні завдання - це ті, які не мають вимог до замовлення, їх можна виконати в будь-якому порядку.

    а Розглянемо три завдання, з часом виконання 2, 2 і 4 години відповідно. Побудуйте два різних графіка на двох процесорах з різним часом завершення, щоб показати, що список пріоритетів все ще має значення для незалежних завдань.

    б Виберіть набір незалежних завдань з різним часом виконання та реалізуйте алгоритм зменшення часового списку та алгоритм критичного шляху. Що ви спостерігаєте?

    c Чи завжди буде використовувати спадний часовий список або алгоритми критичного шляху з незалежними завданнями завжди виробляти оптимальний графік? Чому чи чому ні?

    d Чи буде використання спадного часового списку або алгоритмів критичного шляху з незалежними завданнями завжди виробляти однаковий графік? Чому чи чому ні?

    1. У групі виберіть десять завдань, необхідних для того, щоб влаштувати день народження для друга або дитини (наприклад, прибирання будинку або покупка торта). Визначте вимоги до порядку виконання завдань, створіть диграф та плануйте завдання для двох людей.

    29-37: В кінці глави було зазначено, що не існує алгоритму для визначення оптимальності довільного розкладу, але є особливі випадки, коли ми можемо визначити, що графік дійсно оптимальний. У кожному з наступних сценаріїв визначте

    1. Якщо сценарій навіть можливий
    2. Незалежно від того, чи може бути оптимальний графік
    3. Чи можемо ми бути впевнені, що графік є оптимальним.
    1. Робота має критичний час 30 годин, а час закінчення графіка на 2 процесорах становить 30 годин.
    2. Сума всіх разів завдання для завдання становить 40 годин, а час закінчення графіка на 2 процесорах склало 15 годин.
    3. Сума всіх завдань часу для завдання становить 100 годин, критичний час завдання - 40 годин, а час закінчення графіка на 2 процесорах - 50 годин.
    4. Сума всіх завдань часу для завдання становить 50 годин, а час закінчення графіка на 2 процесорах - 40 годин.
    5. Робота має критичний час 30 годин, а час закінчення графіка на 3 процесорах становить 20 годин.
    6. Сума всіх разів завдання для завдання становить 60 годин, а час закінчення графіка на 3 процесорах склало 20 годин.
    7. Критичний час для роботи - 25 годин, а час закінчення графіка на 2 процесорах - 30 годин.
    8. Сума всіх разів завдання для завдання становить 20 годин, а час закінчення графіка на 2 процесорах - 25 годин.
    9. Виходячи з ваших спостережень у попередніх сценаріях, напишіть рекомендації щодо того, коли ви зможете визначити, що графік є оптимальним.