Skip to main content
LibreTexts - Ukrayinska

7.4: Вибір списку пріоритетів

  1. Last updated
  2. Save as PDF
  • Page ID
    66477

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ми вивчимо два алгоритми вибору списку пріоритетів.

    Алгоритм зменшення часу

    Алгоритм зменшення часу використовує підхід, намагаючись якомога швидше вивести дуже довгі завдання, поставивши їх на перше місце у списку пріоритетів.

    Алгоритм зменшення часу

    Створіть список пріоритетів, перерахувавши завдання в порядку від найдовшого часу виконання до найкоротшого часу завершення.

    Приклад 3

    Розглянемо проблему планування, представлену на диграфі нижче. Створіть список пріоритетів за допомогою алгоритму спадного списку часу, а потім використовуйте його для планування для двох процесорів за допомогою алгоритму обробки списків.

    sc4.svg

    Рішення

    Щоб використовувати алгоритм спадного списку часу, ми створюємо наш список пріоритетів, перерахувавши завдання в порядку від найдовшого часу завдання до найкоротшого часу завдання. Якщо є краватка, ми спочатку перерахуємо завдання з меншим номером завдання (не з будь-якої вагомої причини, а лише для узгодженості).

    Для цього диграфа алгоритм зменшення часу створить список пріоритетів:

    \(\mathrm{T}_{6}(10), \mathrm{T}_{3}(7), \mathrm{T}_{10}(7), \mathrm{T}_{1}(6), \mathrm{T}_{5}(5), \mathrm{T}_{4}(4), \mathrm{T}_{7}(4), \mathrm{T}_{2}(3), \mathrm{T}_{8}(3), \mathrm{T}_{9}(2)\)

    Після того, як у нас є список пріоритетів, ми можемо створити розклад за допомогою алгоритму обробки списку. З двома процесорами ми отримаємо:

    Час 0: Ми визначаємо готові завдання, а також\(\mathrm{T}_{3}\)\(\mathrm{T}_{1}\) призначаємо\(\mathrm{P}_{1}\) і\(\mathrm{P}_{2}\)

    Список пріоритетів:\(\mathrm{T}_{6}, \cancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \cancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, (\mathrm{T}_{4}), \mathrm{T}_{7}, (\mathrm{T}_{2}), \mathrm{T}_{8}, \mathrm{T}_{9}\)

    clipboard_e703f720a08aad265afd1225075591440.png

    Час 6:\(\mathrm{P}_{2}\) завершується\(\mathrm{T}_{1}\). Ніякі нові завдання не стають готовими,\(\mathrm{T}_{4}\) тому доручено\(\mathrm{P}_{2}\).

    Список пріоритетів:\(\mathrm{T}_{6}, \cancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \cancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, (\mathrm{T}_{2}), \mathrm{T}_{8}, \mathrm{T}_{9}\)

    clipboard_ec24ebf2ce33459b8974ae360bc36959b.png

    Час 7:\(\mathrm{P}_{1}\) завершується\(\mathrm{T}_{3}\). Ніякі нові завдання не стають готовими,\(\mathrm{T}_{2}\) тому доручено\(\mathrm{P}_{1}\).

    Список пріоритетів:\(\mathrm{T}_{6}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \cancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, \cancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

    clipboard_efe5bc017ef0173e4a1df6c03eff62c90.png

    Час 10: Обидва процесори завершують свої завдання. \(\mathrm{T}_{6}\)стає готовим, і покладається на\(\mathrm{P}_{1}\). Ніякі інші завдання не готові, так що\(\mathrm{P}_{2}\) холості.

    Список пріоритетів:\(\cancel{\mathrm{T}_{6}}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \xcancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, \xcancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

    clipboard_e512e9c2ed991ded58e7a27d44142a55a.png

    Час 20: З\(\mathrm{T}_{6}\) повним,\(\mathrm{T}_{5}\) і\(\mathrm{T}_{7}\) стати готовим, і призначаються\(\mathrm{P}_{1}\) і\(\mathrm{P}_{2}\) відповідно.

    Список пріоритетів:\(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \cancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \cancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

    clipboard_e489ac776b4f4bbdf786ee597826eae80.png

    Час 24:\(\mathrm{P}_{2}\) завершується\(\mathrm{T}_{7}\). Ніякі новинки не стають готовими, так що\(\mathrm{P}_{2}\) холостий.

    Час 25:\(\mathrm{P}_{1}\) завершується\(\mathrm{T}_{5}\). \(\mathrm{T}_{8}\)і\(\mathrm{T}_{9}\) стають готовими, і призначаються.

    Список пріоритетів:\(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \xcancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \xcancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \cancel{(\mathrm{T}_{8})}, \cancel{(\mathrm{T}_{9})}\)

    clipboard_e5e6ece99dbe18a75824499c1d29e6a8d.png

    Час 27:\(\mathrm{T}_{9}\) завершено. Ніяких предметів не готово, так що\(\mathrm{P}_{2}\) холостий хід.

    Час 28:\(\mathrm{T}_{8}\) завершено. \(\mathrm{T}_{10}\)стає готовим, і покладається на\(\mathrm{P}_{1}\).

    Список пріоритетів:\(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \cancel{(\mathrm{T}_{10})}, \xcancel{(\mathrm{T}_{1})}, \xcancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \xcancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \xcancel{(\mathrm{T}_{8})}, \xcancel{(\mathrm{T}_{9})}\)

    clipboard_e3136d11371231accc1af61a55c53d6b1.png

    Це наш завершений графік, з часом закінчення 35.

    Використовуючи алгоритм зменшення часу, список пріоритетів призвів до розкладу з часом закінчення 35. Це добре? Безумовно, схоже, в цьому графіку було багато простоїв. Щоб отримати якесь уявлення про те, наскільки хороший чи поганий цей графік, ми могли б обчислити критичний час, мінімальний час для завершення роботи. Щоб знайти це, шукаємо послідовність завдань з найбільшим загальним часом виконання. Для цього диграфа ця послідовність виглядатиме:\(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) із загальним часом послідовності 28. З цього можна зробити висновок, що наш графік не жахливий, але є ймовірність того, що існує кращий графік.

    Спробуйте зараз 2

    Визначте список пріоритетів для диграфа з Try it Now 1 за допомогою алгоритму зменшення часу.

    Відповідь

    \(\mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4,} \mathrm{T}_{2}, \mathrm{T}_{9}, \mathrm{T}_{5}, \mathrm{T}_{3}, \mathrm{T}_{6,} \mathrm{T}_{8}\)

    Алгоритм критичного шляху

    Послідовність завдань в диграфі називається контуром. У попередньому прикладі ми бачили, що критичний шлях диктує мінімальний час завершення графіка. Можливо, тоді, було б сенс розглянути критичний шлях при створенні нашого графіка. Наприклад, в останньому графіку процесори почали працювати над завданнями 1 і 3 тому, що вони були більш тривалими завданнями, але починаючи з завдання 2 раніше дозволило б почати роботу над довгим завданням 6 раніше.

    Алгоритм критичного шляху дозволяє створити список пріоритетів на основі уявлення про критичні шляхи.

    Алгоритм критичного шляху (версія 1)
    1. Знайдіть критичний шлях.
    2. Перше завдання на критичному шляху додається до списку пріоритетів.
    3. Вилучити це завдання з диграфа
    4. Повторіть, знайшовши новий критичний шлях з переглянутим диграфом
    Приклад 4

    Оригінальний диграф з Прикладу 3 має критичний шлях,\(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) тому\(\mathrm{T}_{2}\) він додається першим до списку пріоритетів. Видаливши\(\mathrm{T}_{2}\) з диграфа, тепер він виглядає так:

    sc5.svg

    Рішення

    Критичний шлях (найдовший шлях) у решті диграфа\(\mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) тепер\(\mathrm{T}_{6}\) додається до списку пріоритетів та видаляється.

    sc6.svg

    Тепер є два шляхи з однаковою найдовшою довжиною:\(\mathrm{T}_{1}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10}\) і\(\mathrm{T}_{3}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{10}\). Ми можемо додати\(\mathrm{T}_{1}\) до списку пріоритетів (або\(\mathrm{T}_{3}\) - ми зазвичай додаємо той, який має менший номер елемента) і видалити його, і продовжити процес.

    Я впевнений, що ви можете собі уявити, що пошук критичного шляху кожного разу, коли ви видаляєте завдання з диграфа, стане дійсно втомлюючим, особливо для великого диграфа. На практиці алгоритм критичного шляху реалізується спочатку працюючи з кінця назад. Це називається алгоритмом зворотного потоку.

    Алгоритм зворотного потоку
    1. Введіть вершину «кінця» та призначте їй час 0, показаний у [дужках]
    2. Переміщайтеся назад до кожної вершини, яка має стрілку до кінця, і призначте їй критичний час
    3. Від кожної з цих вершин рухайтеся назад і призначте ці вершини критичних часів. Зверніть увагу, що критичним часом для попередньої вершини буде час цього завдання плюс критичний час для пізнішої вершини.

    Приклад: Розглянемо цей сегмент диграфа.

    sc7.svg

    При цьому, якщо Т2 вже було визначено критичний час 10, то Т1 матиме критичний час 5+10 = 15

    sc8.svg

    Якщо ви вже призначили критичний час вершині, замініть його, лише якщо новий час більше.

    Приклад: На диграфі нижче Т1 повинен бути позначений критичним часом 16, так як він довший 5+10 і 5+11.

    sc9.svg

    4. Повторюйте до тих пір, поки всі вершини не будуть позначені критичним часом

    Після того, як ви виконали алгоритм зворотного потоку, ви можете легко створити список пріоритетів критичного шляху, використовуючи критичні часи, які ви щойно знайшли.

    Алгоритм критичного шляху (версія 2)
    1. Застосувати алгоритм зворотного потоку до диграфа
    2. Створіть список пріоритетів, перерахувавши завдання в порядку від найдовшого критичного часу до найкоротшого критичного часу

    Цю версію алгоритму критичного шляху, як правило, буде простіше реалізувати.

    Приклад 5

    Застосовуючи це до нашого диграфа з попереднього прикладу, ми починаємо застосовувати алгоритм зворотного потоку.

    Рішення

    Додаємо кінцеву вершину і даємо їй критичний час 0.

    sc10.svg

    Потім ми повернемося до\(\mathrm{T}_{4}, \mathrm{T}_{9},\) і\(\mathrm{T}_{10}\), позначивши їх критичними часами

    sc11.svg

    Від кожної вершини, зазначеної критичним часом, йдемо назад. \(\mathrm{T}_{7}\), наприклад, отримає позначку з критичним часом 11 — час завдання 4 плюс критичний час 7 для\(\mathrm{T}_{10}\). Для\(\mathrm{T}_{5}\), є два шляхи до кінця. Використовуємо довше, маркування Т 5 з критичним часом\(5+7 = 12\).

    sc12.svg

    Продовжуйте процес, поки всі вершини не будуть позначені. Зверніть увагу, що критичний час для\(\mathrm{T}_{5}\) закінчився був замінений пізніше з ще довшим шляхом через\(\mathrm{T}_{8}\).

    sc13.svg

    Тепер ми можемо швидко створити список пріоритетів критичного шляху, перерахувавши завдання в порядку зменшення критичного часу:

    Список пріоритетів:\(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{4}, \mathrm{T}_{9}\)

    Застосовуючи цей список пріоритетів за допомогою алгоритму обробки списків, отримуємо розклад:

    clipboard_ef29844773f30d594f64ac4eec0cfb679.png

    У цьому конкретному випадку ми змогли досягти мінімально можливого часу завершення з цим графіком, припускаючи, що цей графік є оптимальним. Це, звичайно, не завжди так.

    Спробуйте зараз 3

    Визначте список пріоритетів для диграфа від Try it Now 1 за допомогою алгоритму критичного шляху.

    Відповідь

    Застосовуючи алгоритм зворотного потоку, отримуємо ось що:

    sc16.svg

    Список пріоритетів критичного шляху:\(\mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4}, \mathrm{T}_{2}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{9}, \mathrm{T}_{3}, \mathrm{T}_{6}\)

    Приклад 6

    Цей приклад покликаний показати, що алгоритм критичного шляху не завжди працює чудово. Плануйте завдання на диграфі нижче на трьох процесорах, використовуючи алгоритм критичного шляху.

    sc14.svg

    Рішення

    Щоб створити список пріоритетів критичного шляху, ми могли б спочатку застосувати алгоритм зворотного потоку:

    sc15.svg

    Це дає список пріоритетів критичного шляху:\(\mathrm{T}_{1}, \mathrm{T}_{6}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{4}, \mathrm{T}_{5}, \mathrm{T}_{9}, \mathrm{T}_{2}, \mathrm{T}_{3}\).

    Застосування алгоритму обробки списків до цього списку пріоритетів призводить до розкладу:

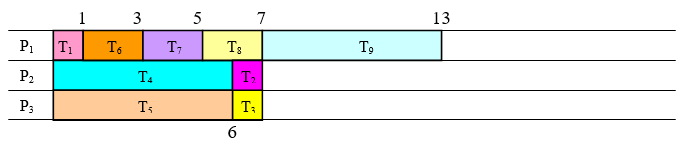
    clipboard_e9bf290d6eedb6f0b1f58037dbaa4efb2.png

    Цей графік має час закінчення 13.

    Спостерігаючи, ми можемо побачити, що набагато кращий графік існує для наведеного вище прикладу:

    clipboard_eddd4095caab1bdf49b5be7a88733fcd1.png

    У більшості випадків алгоритм критичного шляху призведе до дуже хорошого графіку. Бувають випадки, на зразок цього, де не буде. На жаль, немає відомого алгоритму завжди виробляти оптимальний графік.